1 Температурное поле-совокупность значений температур в каждой точке тела, в каждый момент времени.

t=f(x,y,z,τ)-нестационарное поле(периодические процессы)

если t(τ)=const – имеем стационарное t=f(x,y,z) (непрерывное)

t=f(y) – простейшее стационарное температурное поле.

Точки имеющие одинаковую температуру образуют изотермическую поверхность. Изотермические поверхности не пересекаются .

Градиент температуры (grad T) =

Частная производная температура по нормали

Вектор направлен в сторону наибольшего быстрого роста температуры

Grad(T) – пространственная характеристика температурного поля

Grad T =

Для стационарного температурного поля grad T =

Движущая сила теплообмена явл. Разность температур или grad T.

Характеристики теплового поля.

Тепловой поток характеризуется:

1. Мощностью теплового потока Q (Дж/с) (Вт) – кол-во теплоты которое проходит ч/з поверхность в единицу времени;

2. Плотность теплового потока

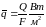(средний по поверхности) – кол-во теплоты, которое проходит в единицу времени ч/з единицу поверхности.

Виды теплообмена.

3 способа переноса теплоты:

1. Теплопроводность – перенос теплоты молекулярным механизмом, т.е. в результате взаимодействия между частицами.

2. Конвекция – перемещение объёмов подвижной среды. Всегда сопровождается теплопроводностью, отсюда конвективный теплообмен – совместный теплообмен конвекции с теплопроводностью. Конвективный ТО – обмен в подвижной среде.

3. Излучение – перенос энергии электромагнитными волнами.

2 Теплопроводность. Закон Фурье.

Перенос теплоты в результате взаимодействия между микро частицами. Основной закон теплопроводности этот закон Фурье - плотность теплового потока теплопроводности пропорциональна градиенту температуры.

где - коэффициент теплопроводности (Вт/(м*к)), физическое свойство вещества характеризует способность тела проводить теплоту. - зависит от агрегатного состояния, температуры, давления и т. д.

Наименьший коэффициент теплопроводности имеют газы = 0,00009-0,009 (Вт/(м*к)),

металл в 1000 раз больше

жидкость 0,07-0,7

твердые тела 0,3-4

- в газах соударение молекул,

- в твердых телах волна колебаний

- в жидкостях и то и другое выше сказанное

- в металлах перемещение свободных электронов.

Теплоизоляционные материалы – это материалы с низким коэффициентом теплопередачи 0,05.

3 Стационарная теплопроводность через плоскую стенку

1) Однородная плоская стенка (Рис.9.2.).

Температуры поверхностей стенки: t_ст1 и t_ст2.

Плотность теплового потока:

q = -λ∙ ∂t/∂n = - λ∙ ∂t/∂x = - λ∙ (t_cт2 - t_cт1)/(x_cт2 - x_cт1)∙

или

q = λ∙ (t_cт2 - t_cт1)/(x_cт2 - x_cт1)∙ Δt/Δx (9.13)

Δt - температурный напор;

δ - толщина стенки.

Тогда

q = λ/δ∙(t_ст1 – t_ст2) = λ/δ∙Δt, (9.14)

Если R =δ/λ -термическое сопротивление теплопроводности стенки [(м²∙К)/Вт], то плотность теплового потока:

q = (t_ст1 – t_ст2)/R . (9.15)

Общее количество теплоты, которое передается через поверхность F за время τ определяется:

Q = q∙F∙τ = (t_ст1 – t_ст2)/R·F∙τ . (9.16)

Температура тела в точке с координатой х находится по формуле:

t_x = t_ст1 – (t_ст1 – t_ст2)∙x/ δ . (9.17)

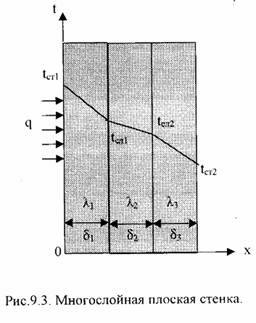
2) Многослойная плоская стенка. Рассмотрим 3-х слойную стенку (Рис.9.3). Температура наружных поверхностей стенокt_ст1 и t_ст2, коэффициенты теплопроводности слоев: λ₁, λ₂, λ₃, толщина слоев: δ₁, δ₂, δ₃. Плотности тепловых потоков через каждый слой стенки:

q = λ₁/δ₁∙(t_ст1 – t_сл1) , (9.18)

q = λ₂/δ₂∙(t_сл1 – t_сл2) , (9.19)

q = λ₃/δ₃∙(t_сл2 – t_ст2) , (9.20)

Решая эти уравнения, относительно разности температур и складывая, получаем:

q = (t₁ – t₄)/(δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃) = (t_ст1 – t_ст4)/R_o , (9.21)

где: R_o = (δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃) – общее термическое сопротивление теплопроводности многослойной стенки.

Температура слоев определяется по следующим формулам:

t_сл1 = t_ст1 – q∙(δ₁/λ₁). (9.22)

t_сл2 = t_сл1 – q·δ₂/λ₂). (9.23)

4 Стационарная теплопроводность через цилиндрическую стенку однослойную и многослойную.

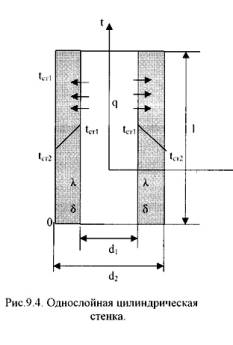
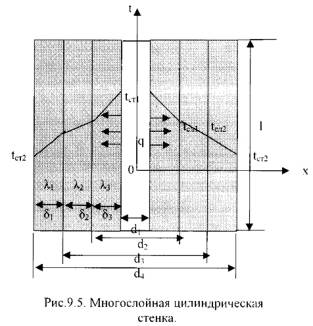
1). Однородная цилиндрическая стенка. Рассмотрим однородный однослойный цилиндр длиной l, внутренним диаметром d1и внешним диаметром d2 (Рис.9.4). Температуры поверхностей стенки –tст1 и tст2. Уравнение теплопроводности по закону Фурье в цилиндрических координатах: Q = - λ∙2∙π∙r ·l· ∂t / ∂r (9.24)илиQ = 2·π·λ·l·Δt/ln(d2/d1), (9.25)где: Δt = tст1 – tст2 – температурный напор; λ – κоэффициент теплопроводности стенки. Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут:ql = Q/l =2·π·λ·Δt /ln(d2/d1), [Вт/м]. (9.26)Температура тела внутри стенки с координатойdх:tx = tст1 – (tст1 – tст2) ·ln(dx/d1) / ln(d2/d1). (9.27)2). Многослойная цилиндрическая стенка. Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.9.5). Температура внутренней поверхности стенки –tст1, температуранаружнойповерхности стенки –tст2, коэффициенты теплопроводности слоев -λ1, λ2, λ3, диаметры слоев d1, d2, d3, d4.

Тепловые потоки для слоев будут:

1-й слойQ = 2·π· λ1·l·(tст1 – tсл1)/ ln(d2/d1), (9.28)

2-й слой Q = 2·π·λ2·l·(tсл1 – tсл2)/ ln(d3/d2), (9.29)

3-й слой Q = 2·π·λ3·l·(tсл2 – tст2)/ ln(d4/d3), (9.30)Решая полученные уравнения, получаем для теплового потока через многослойную стенку:Q = 2·π·l·(tст1 – tст2) / [ln(d2/d1)/λ1 + ln(d3/d2)/λ2 + ln(d4/d3)/λ3 ледующих уравнений:tсл1 = tст1 – ql·ln(d2/d1) 2·π·λ1 . (9.33) tсл2 = tсл1 – ql·ln(d3/d2) / 2·π·λ2 .

5 Граничные условия третьего рода (теплопередача). Передача теплоты из одной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде. Рассмотрим теплопередачу через однородную и многослойную плоские стенки.

П усть плоская однородная стенка имеет толщину δ (рис. 2.3). Заданы коэффициент теплопроводности стенки λ, температуры окружающей среды tf1 и tf2, а также коэффициенты теплоотдачи 1 и 2; будем считать, что величины tf1 , tf2 ,1 и 2 постоянны и не меняются вдоль поверхности. Это позволяет рассматривать изменение температуры жидкостей и стенки только в направлении, перпендикулярном плоскости стенки.

При заданных условиях необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхности стенки. Плотность теплового потока от горячей жидкости к стенке определяется уравнением

П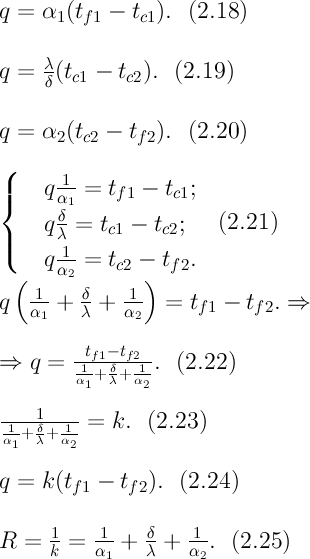 ри стационарном тепловом режиме та же плотность теплового потока, обусловленная теплопроводностью через твердую стенку - (2.19). Тот же тепловой поток передается от второй поверхности стенки к холодной жидкости за счет теплоотдачи - (2.20). Уравнения (2.18) - (2.20) можно собрать в систему (2.21). Если сложить равенства (2.21) почленно, то получим выражение из которого находим плотность теплового потока, Вт/м2 - (2.22). Если ввести обозначение (2.23) (единица измерения - Вт/м2×К), то уравнение (2.22) можно записать в виде (2.24). Величина k имеет ту же размерность, что и , и называется коэффициентом теплопередачи. Коэффициент теплопередачи k характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус.Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи - (2.25). Из (2.25) видно, что полное термическое сопротивление складывается из частных термических сопротивлений 1/1, δ/λ и 1/2, причем 1/1=R1 — термическое сопротивление теплоотдачи от горячей жидкости к поверхности стенки; δ/λ=Rс — термическое сопротивление теплопроводности стенки;1/2=R2 — термическое сопротивление теплоотдачи от поверхности стенки к холодной жидкости.Поскольку общее термическое сопротивление состоит из частных термических сопротивлений, то совершенно очевидно, что для многослойной стенки нужно учитывать термическое сопротивление каждого слоя. Если стенка состоит из n слоев, то полное термическое сопротивление теплопередачи через такую стенку будет равно:

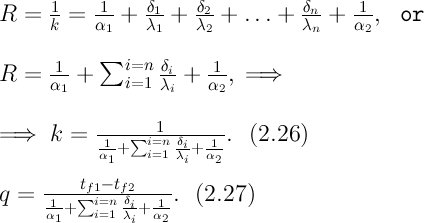
6 Выделим участок длиной L

T=f(r); t( )=const;

При λ =const температура изменяется по логарифмическому закону

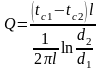
При %

Вт/м

Вт/м;

Многослойная цилиндрическая стенка

Для n слоёв

7 Пути интенсификации теплопередачи.

увеличение прочности теплового потока q вт/м

q=K

1. Растет

2. преимущества роста K; ;взять больше имеет смысл если << 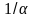,преимущественно изменяют коэффициенты

а)увеличивается скорость для этого требуется если , то

б) турбулизировать поток

если (сильно отличаются),

;( ) , увеличить нужно из коэф-тов теплоотдачи, можно компенсировать малый коэф. Теплоотдачи оребрения поверхности нужно делать со стороны меньшего коэф. Теплоотдачи.