Часть 4

ι

КОЛЕБАНИЯ И ВОЛНЫ

1. Механические колебания

φ Уравнение гармрнических колебаний и его решение!

χ = α cos (ω₀/+α), (4.1а)

г

где щ—собственная частота колебаний.

φ Уравнение затухающих колебаний и его решение:

χ + 2βχ -f ωΐχ=0, X=яое^-^ cos (ω*+α), (4 Л 6j

где β — коэффициент затухания, ω — частота затухающих колебаний]

^ω = IA³O "Ρ²· (4 Л в)

φ Логарифмический декремент затухания λ и добротность Qj

λ = β7\ Q = π/λ, (4 Л г)

где 7* = 2π/ω.

φ Уравнение вынужденных колебаний и его установившееся решение:

ф Максимум амплитуды смещения достигается при

®pe3=V®J-2p«. (4 Л ж)

4.1« Точка совершает колебания вдоль оси а: по закону χ =* = α cos (ωί — π/4). Построить примерные графики:

а) смещения X₉ проекции скорости V_x и проекции ускорения W_x как функций времени t\

б) проекции скорости V_x и проекции ускорения W_x как функций координаты х.

2. Некоторая точка движется вдоль оси χ по закону χ =» = a sin² (ωί — π/4). Найти:

а) амплитуду и период колебаний; изобразить график χ

б) проекцию скорости V_x как функцию координаты х\ изобра­зить график V_x (х).

3. Частица совершает гармонические колебания вдоль оси χ около' положения равновесия χ = 0. Частота колебаний ω = = 4,00 рад/с. В некоторый момент координата частицы X₀ = 25,0 см и ее скорость V_xo = 100 см/с. Найти координату χ и скорость V_x частицы через t = 2,40 с после этого момента.

4. Найти круговую частоту и амплитуду гармонических коле­баний частицы, если на расстояниях X₁ и X₂ от положения равнове­сия ее скорость равна соответственно U₁ и V₂.

5. Точка совершает гармонические колебания вдоль некоторой прямой с периодом T = 0,60 с и амплитудой а = 10,0 см. Найти среднюю скорость точки за время, в течение которого она проходит

путь а/2:

а) из крайнего положения;

б) из положения равновесия.

6. В момент t = 0 точка начинает совершать колебания вдоль оси χ по закону χ = a sin ωί. Найти за первые 3/8 периода поеле

начала движения:

а) среднее значение проекции ее вектора скорости (V_x);

б) модуль среднего вектора скорости j<v)j;

в) среднее значение модуля скорости <ι>).

7. Частица движется вдоль оси χ по закону χ — a cos ωί. Найти путь, который она пройдет за промежуток времени от t = Q до t.

8. В момент t = 0 частица начинает двигаться вдоль оси χ так, что проекция ее скорости меняется по закону v_x = 35 cos πί см/с, где'/ в секундах. Найти путь, который пройдет эта частица за пер­вые i = 2,80 с после начала движения.

9. Частица совершает гармонические колебания вдоль оси χ по закону X = a cos ωί. Считая вероятность P нахождения частицы в интервале от —а до +а равной единице, найти зависимость от χ плотности вероятности dP/dx, где dP — вероятность нахождения частицы в интервале от л: до χ + dx. Изобразить график dP/dx в за­висимости от X.

10. Найти графически амплитуду а колебаний, которые воз­никают при сложении следующих колебаний одного направ­ления: ,

а) X₁ - 3,0 cos (ωί + π/3), X₂ = 8,0 sin (ωί + π/б); ^

б) X₁ = 3,0 cos ωί, X₂ = 5,0 cos (ωί + π/4), X₃ = 6,0 sin ωί.

11. Точка участвует одновременно в двух колебаниях одного направления, которые происходят по законам X₁ = a cos ωί и х_а = = a cos 2 ωί. Найти максимальную скорость точки.

12. При сложении двух гармонических колебаний одного на­правления результирующее колебание точки имеет вид χ = = α cos 2,Ii-cos 50,0/, где ί в секундах. Найти круговые частоты складываемых колебаний и период биений результирующего коле- бзния

» 4.13. Точка А колеблется по определенному гармоническому закону в К'-системе отсчета, которая в свою очередь совершает

гармонические колебания по отношению к /С-системе. Оба колеба­ния происходят вдоль одного и того же направления. При частоте колебаний /С'-системы 20 или 24 Гц частота возникающих бие­ний точки А в /С-системе оказывается равной v. При какой частоте колебаний /С'-системы частота биений точки А станет равной 2v?

14. Точка движется в плоскости ху по закону χ = a sin ωέ₉ у == Ъ cos со/, где α, b и ω — положительные постоянные. Найти:

а) уравнение траектории точки у (х) и направление ее движения по этой траектории;

б) ускорение точки w в зависимости от ее радиус-вектора г относительно начала координат.

14. Найти уравнения траектории точки у (х), если она дви­жется по законам:

а) χ = a sin ωί, у = a sin 2ωί\

б) χ = a sin ω/, у = a cos 2ω£.

Изобразить графики этих траекторий.

14. Частица массы т находится в одномерном потенциаль­ном поле, где ее потенциальная энергия зависит от координа­ты χ как U (х) = U₀ (1 — cos ах)у U₀ и о — некоторые постоян­ные. Найти период малых колебаний частицы около положения равновесия.

15. Тот же вопрос, что и в предыдущей задаче, но потенциаль­ная энергия имеет вид U (х) = а/х² — bj X₉ где а и b — некоторые положительные постоянные.

16. Найти период малых вертикальных колебаний шарика массы т = 40 г, укрепленного на середине горизонтально натяну­той струны длины / = 1,0 м. Натяжение струны считать постоянным и равным F = ЮН.

17. Определить период малых колебаний математического маятника — шарика, подвешен­ного на нити длины I = 20 см, если он находится в жидкости, плотность которой в η = 3,0 раза меньше плотности шарика. Сопротивление жидко­сти считать пренебрежимо малым.

18. Шарик подвесили на нити длины I к точке О стенки, составляющей небольшой угол α с вертикалью (рис. 4.1). Затем нить с ша-

Рис. 4.1. риком отклонили на небольшой угол β (β > α) и отпустили. Считая удар шарика о стенку абсолютно упругим, найти период колебаний такого маятника.

4.21. Маятниковые часы установили в кабине лифта, которая начала- подниматься с постоянным ускорением W₉ причем w<ig. На высоте h ускорение кабины изменило свое направление на про­тивоположное, оставшись по модулю тем же. Через сколько вре\1ени после начала движения показания часов окажутся вер­ными?

22. Вычислить период малых колебаний ареометра (рис, 4.2), •которому сообщили небольшой толчок в вертикальном направлении. Масса ареометра т = 50 г, радиус его трубки г = 3,2 мм, плотность жидкости ρ = 1,00 г/см³. Сопротивление жидкости считать пренебрежимо малым.

23. Имеется недеформированная пружина жесткости χ = 13 Н/м, концы которой закреп­лены. В точке, отстоящей от одного из концов пружины на η = 1/3 ее длины, укрепили не­большое тело массы т = 25 г. Пренебрегая мас­сой пружины, найти период малых продольных колебаний данного тела. Силы тяжести нет.

24. Определить период малых продольных колебаний тела массы т в системе (рис. 4.3),

Ч-

Рис. 4.2.

если жесткости пружинок равны X₁ и X₂, а их массы и трение пренебрежимо малы.

Рис. 4.5.

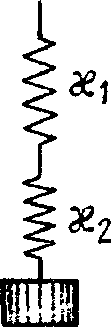
22. Найти период малых вертикальных колебаний тела массы т в системе (рис. 4.4). Жесткости пружинок равны X₁ и х₂, а их массы пренебрежимо малы.

22222

4.26. Небольшое тело массы т закреплено на середине натянутой струны

^A/VVj КАЛЛЛ/2

/77

Рис. 4.4.

/^τττττττττττ^τττττττζ

077777777777777777777/, Рис. 4.3.

длины 2L Натяжение струны в положении равновесия равно T₀. Найти угловую частоту малых колебаний тела в поперечном направ­лении. Масса струны пренебрежимо мала, поле тяжести отсутствует.

27. Определить период колебаний ртути массы т = 200 г, налитой в изогнутую трубку (рис. 4.5), правое колено которой со­ставляет угол θ = 30°

с вертикалью. Площадь > _ — ,„ j

7/7777/,

Рис. 4.6.

ω

77777777,

сечения канала трубки S = 0,50 см². Вязкостью ртути пренебречь.

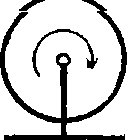
27. на рис. 4.6. Расстояние между осями коэффициент трения между стержнем и бло­ками k = 0,18. Показать, что стержень будет совершать гармо­нические колебания. Найтй ш период.

    161

    Однородный стержень положили на два быстро вращающих­ся блока, как показано блоков I = 20 см,

6 И. Е. Иродов

27. Представим себе шахту, пронизывающую Землю по ее оси вращения. Считая Землю за однородный шар и пренебрегая сопро­тивлением воздуха, найти:

а) закон движения тела, упавшего в шахту;

б) сколько времени понадобится этому телу, чтобы достигнуть противоположного конца шахты;

в) скорость тела в центре Земли.

27. 

    Рис. 4.7.

    δ

    Найти период малых колебаний математического маят­ника длины /, если его точка подвеса О движется относительно по­верхности Земли в произвольном направлении с постоянным уско­рением w (рис. 4.7). Вычислить этот период, если / = 21 см, w = g/2 и угол между векторами w и g β = 120°.

M

Рис. 4.9.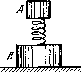

CTvVl

Рис. 4.8.

27. В установке (рис. 48) муфта M массы т = 0,20 кг закреп­лена между двумя одинаковыми пружинками, общая жесткость которых κ = 20 Н/м. Муфта без трения может скользить по гори­зонтальному стержню AB. Установка вращается с постоянной угло­вой скоростью ω = 4,4 рад/с вокруг вертикальной оси, проходящей через середину стержня. Найти период малых колебаний муфты. При каком значении ω колебаний муфты не будет?

28. Доска с лежащим на ней бруском совершает горизонталь­ные гармонические колебания с амплитудой а = 10 см. Найти коэффициент трения между доской и бруском, если последний начи­нает скользить по доске, когда ее период колебания меньше T = 1,0 с.

29. Найти зависимость от времени угла отклонения матема­тического маятника длины 80 см, если в начальный момент маятник:

а) отклонили на угол 3,0° и без толчка от­пустили;

б) находился в состоянии равновесия и его нижнему концу сообщили горизонтальную ско­рость 0,22 м/с;

в) отклонили на 3,0° и его нижнему концу сообщили скорость 0,22 м/с, направленную к положению равновесия.

4.34. Тело А массы m_x = 1,00 кг и тело В массы т₂ = 4,10 кг соединены между собой пру­жиной, как показано на рис. 4.9. Тело А совершает свободные вер­тикальные гармонические колебания с амплитудой а = 1,6 см и частотой ω = 25 рад/с. Пренебрегая массой пружины, найти

наибольшее и наименьшее значения силы давления этой системы на опорную плоскость.

35. Доска, на которой лежит тело массы т, начинает двигаться вертикально вверх по закону у = а (1 — cos ωί), где у — смещение из начального положения, ω = 11 рад/с. Найти:

а) силу давления тела на доску в зависимости от времени, если а = 4,0 см; изобразить график этой зависимости;

б) минимальную амплитуду колебания доски, при которой тело начнет отставать от нее;

в) амплитуду колебания доски, при которой тело подскочит на высоту h = 50 см относительно начального положения (в мо­мент t = 0).

35. К нерастянутой пружине, верхний конец которой закреп­лен, подвесили и без толчка отпустили тело массы т. Жесткость пружины κ. Пренебрегая ее массой, найти:

а) закон движения тела у (t), где у — его смещение из началь­ного положения;

б) максимальное и минимальное натяжения пружины в процессе движения.

35. Частица массы т движется под действием силы F = —amr, где α — положительная постоянная, г — радиус-вектор частицы относительно начала координат. Найти траекторию ее движения, если в начальный момент г = r₀i и скорость ν = u₀j, где i и j — орты осей хи у.

36. Тело массы т висит на пружине, прикрепленной к потолку кабины лифта. Жесткость пружины κ. В момент f = 0 кабина на­чала подниматься с ускорением w. Пренебрегая массой пружины, найти закон движения груза у (t) относительно кабины лифта, если у (0) = 0 и у (0) = 0. Рас­смотреть два случая:

а) w = const;

б) w = а/, где а — постоянная.

35. Тело массы т = 0,50 кг висит на резино­вом шнуре с коэффициентом упругости k = 50 Н/м. Найти максимальное расстояние, на которое можно оттянуть вниз тело, чтобы его колебания еще но­сили гармонический характер. Какова при этом энергия колебаний тела?

36. Тело массы т упало с высоты h на чашку пружинных весов (рис. 4.10). Массы чашки и пружины пренебрежимо малы, жесткость послед­ней κ. Прилипнув к чашке, тело начинает совер­шать гармонические колебания в вертикальном направлении. Найти амплитуду колебаний и их энергию.

37. JTl 1 I

    Jll

    сз

    77777777.

    Рис. 4J0.

    В условиях· предыдущей задачи масса чашки равна Λί. Найти амплитуду колебаний в этом случае.

38. 6*

    Частица массы т движется в плоскости ху под действием силы, зависящей от скорости .по закону F = а (ух — χj), где а —

163

положительная постоянная, i и j — орты осей χ и у. В начальный момент t = О частица находилась в точке χ .= у = 0 и имела ско­рость V₀ в направлении орта j. Найти закон движения частицы χ (t)_f у (/), а также уравнение ее траектории.

4.43/Маятник представляет собой легкий тонкостенный сфери­ческий сосуд радиуса R_y который целиком заполнен водой. Сосуд укреплен на легком жестком стержне (рис. 4.11). Расстояние между точкой подвеса О и центром со­суда равно L Во сколько раз изменится период ма­лых колебаний такого маятника после того, как вода замерзнет? Вязкостью воды и изменением ее объема при замерзании пренебречь.

4.44. Найти частоту малых колебаний тонкого однородного вертикального стержня массы т и дли­ны I_y который шарнирно укреплен в точке О (рис. 4.12). Суммарная жесткость пружин κ. Массы пружин пренебрежимо малы.

4.45. Однородный стержень массы ш — 1,5 кг, висящий на двух одинаковых нитях длины / = 90 см (рис. 4.13), повернули на малый угол вокруг вертикальной оси, проходящей через его середину С. При этом нити отклонились на угол α = 5,0°. Затем стержень от­пустили, и он начал совершать малые колебания. Найти:

Рис. 4.11.

а) период колебаний;

б) энергию колебаний стержня.

щ

о

V/////

СС[

№ \ \ \ \

JD

f^yjjj

ъ

ШЯГЧКТОШ

Cf

Рис. 4.14.

Рис. 4.12.

Рис. 4.13.

46. Система (рис. 4.14) состоит из горизонтального однород­ного диска D массы т и радиуса R и тонкого стержня AO₁ коэф­фициент кручения которого k. Найти амплитуду малых крутиль­ных колебаний и их энергию, если в начальный момент диск откло­нили на угол φ₀ из положения равновесия и сообщили ему угловую скорость ф₀.

47. Однородный стержень массы т и длины I совершает малые колебания вокруг горизонтальной оси, проходящей через его верх­ний конец. Найти среднюю за период колебания кинетическую энергию стержня, если в начальный момент его отклонили от вер­тикали на угол O₀ и сообщили ему угловую скорость

4.48. Физический маятник установили так, что его центр тя­жести оказался над точкой подвеса. Из этого положения маятник начал двигаться к положению устойчивого равновесия, которое он прошел с угловой скоростью ω. Пренебрегая трением, найти период малых колебаний этого маятника.

4:49. Физический маятник совершает малые колебания вокруг горизонтальной оси с частотой O₁ = 15,0 рад/с. Если к нему при­крепить небольшое тело массы т = 50 г на расстоянии I =■ 20 см ниже оси, то частота колебаний становится <о₂ = 10,0 рад/с. Найти момент инерции этого маятника относительно оси качания.

50. Два физических маятника совершают малые колебания вокруг одной и той же горизонтальной оси с частотами O₁ и ω₂. Их моменты инерции относительно данной оси равны соответст­венно I₁ и I₂. Маятники привели в состояние устойчивого равнове­сия и скрепили друг с другом. Какова будет частота малых колеба­ний составного маятника?

51. Однородный стержень длины I совершает малые колеба­ния вокруг горизонтальной оси 00', перпендикулярной к стержню и проходящей через одну из его точек. Найти расстояние между центром инерции стержня и осью 00', при котором период колеба­ний будет наименьшим. Чему он равен?

52. Тонкая однородная пластинка в форме равностороннего треугольника с высотой h совершает малые колебания вокруг гори­зонтальной оси, совпадающей с одной из его сторон. Найти период колебаний и приведенную длину данного маятника.

53. 

    Гладкий горизонтальный диск вращают вокруг вертикаль­ной оси О (рис. 4.15) с постоянной угловой скоростью ω. На нем находится тонкий однородный стержень AB длины /, который со­вершает малые колебания вокруг вертикальной оси A_t укрепленной на диске на расстоянии а от оси О. Найти частоту о>₀ этих колебаний.

Рис. 4.15.

4.54. Найти частоту малых колебаний системы, показанной на рис. 4.16. Известны радиус блока R_t его момент инерции / относи­тельно оси вращения, масса тела т и жесткость пружины κ. Массы нити и пружины пренебрежимо малы, нить по блоку не скользит, трения в оси блока нет.

55. Однородный цилиндрический блок массы M и радиуса R может свободно поворачиваться вокруг горизонтальной оси О (рис. 4.17). На блок плотно намотана нить, к свешивающемуся концу которой прикреплен груз Л. Этот груз уравновешивает точечное тело массы т, укрепленное на ободе блока, при определенном зна­чении угла а. Найти частоту малых колебаний системы.

56. 

    Сплошной однородный цилиндр радиуса г катается без скольжения по внутренней стороне цилиндрической поверхности радиуса R_r совершая малые колебания. Найти их период.

Рис. 4.17. Рис. 4.18.

55. Сплошной однородный цилиндр массы т совершает малые колебания под действием двух пружин, общая жесткость которых κ (рис. 4.18). Найти период этих колебаний в отсутствие скольжения.

56. Два кубика, массы которых равны т_х и т₂> соединили не­весомой пружинкой жесткости κ и положили на гладкую горизон­тальную плоскость. Затем кубики не­много сблизили и одновременно отпу­стили. Найти собственную частоту колебаний системы.

4.59. Два шара с массами Hi₁ =

Рис. 4.19. = 1,0 кг и пц = 2,0 кг насажены на

тонкий гладкий горизонтальный стер­жень (рис. 4.19). Шары связаны между собой легкой пружинкой с жесткостью κ = 24 Н/м. Левому шару сообщили начальную скорость V₁ = 12 см/с. Найти:

а) частоту колебаний системы в процессе движения;

б) энергию и амплитуду колебаний.

60. Найти период малых крутильных колебаний системы, со­стоящей из двух дисков, насаженных на тонкий стержень с коэф­фициентом кручения k. Моменты инерции дисков относительно оси стержня равны I₁ и I₂.

61. Модель молекулы CO₂ — три шарика, соединенные одина­ковыми легкими пружинками и расположенные в положении рав­новесия вдоль одной прямой. Такая система может совершать про­дольные колебания двух типов, как показано стрелками на рис. 4.20. Зная массы атомов, найти отношение частот этих колебаний.

62. В закрытом с обоих концов цилиндре, заполненном идеаль­ным газом, находится поршень массы т и площадью S (рис. 4.21).

В состоянии равновесия поршень делит цилиндр на две равные части, каждая объемом V₀. Давление газа р₀. Поршень немного сместили из положения равновесия и отпустили. Найти частоту его колеба­ний, считая процессы в газе адиабатическими, а трение ничтожно малым.

^^{0 с 0}

/у фптт^утляягчэ

Oi ^{0 0 0}

2) ф^тпщшг^тош^

т	I
	1	5

Рис. 4.21,

60. Небольшой шарик массы т = 21 г, подвешенный на изо­лирующей нити на высоте h = 12 см от большой горизонтальной проводящей плоскости, совершает малые колебания (рис. 4.22). После того как ему сообщили некоторый заряд q, период колебаний изменился в η = 2,0 раза. Найти q.

61. Небольшая магнитная стрелка совершает малые колеба­ния вокруг оси, перпендикулярной к вектору индукции магнитного поля. При изменении индукции поля период колебаний стрелки

Рис. 4.20.

уменьшился в η = 5,0 раза. Во сколько раз и как изменилась иц- дукция поля? Затухание колеба­ний пренебрежимо мало.

V₀ —

т

X

®8

/77

V/77777777777777', Рис. 4.22.

60. Контур (рис. 4.23) образован двумя параллельными про­водниками, замыкающим их соленоидом с индуктивностью L и про­водящим стержнем массы т, который может свободно (без трения) скользить по проводникам. Проводники находятся в горизонталь­ной плоскости в однородном вертикальном магнитном поле с ин­дукцией 5. Расстояние между проводниками L В момент /=O стержню сообщили вправо начальную скорость V₀. Найти закон его движения χ (/), если сопротивление контура пренебрежимо мало.

61. Рис. 4.23.

    Катушка индуктивности L соединяет верхние концы двух вертикальных медных шин, отстоящих друг от друга на расстоя­ние L Вдоль шин падает без начальной скорости горизонтальный проводник-перемычка массы т — без нарушения контакта с

шинами. Вся система находится в однородном магнитном поле с ин­дукцией B_t перпендикулярном плоскости шин. Найти закон дви­жения проводника χ (t).

60. Затухающие колебания точки происходят по закону л; = = а₀ sin ωί. Найти:

а) амплитуду колебаний и скорость точки в момент t = 0;

б) моменты времени, когда точка достигает крайних положений.

60. Тело совершает крутильные колебания по закону φ = -= <Рое^-^ cos ωί. Найти:

а «*

а) угловую скорость φ и угловое ускорение φ тела в момент t= 0;

б) моменты времени, когда угловая скорость становится макси­мальной.

60. Точка совершает затухающие колебания с частотой ω и коэффициентом затухания β по закону (4.16). Найти начальную амплитуду а₀ и начальную фазу а, если в момент /=0 смещение точки и проекция ее скорости равны:

а) χ (0) = 0 и v_x (0) = X₀; б) χ (0) = X₀ и V_x (0) = 0.

60. Некоторая точка совершает затухающие колебания с ча­стотой ω = 25 рад/с. Найти коэффициент затухания β, если в на­чальный момент скорость точки равна нулю, а ее смещение из по­ложения равновесия в η — 1,020 раза меньше амплитуды в этот момент.

61. Точка совершает затухающие колебания с частотой ω и коэффициентом затухания β. Найти амплитуду скорости точки как функцию времени Ζ, если в момент ί = 0:

а) амплитуда ее смещения равна а₀;

б) смещение точки χ (0) = 0 и проекция ее скорости V_x (0) = jf₀.

60. Имеются два затухающих колебания с известными перио­дами T и коэффициентами затухания β: T₁ = 0,10 мс, P₁ = 100 с^а и T₂ = 10 мс, β₂ = 10 с"¹. Какое из них затухает быстрее?

61. Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания λ₀ = 1,50. Каким будет логарифмический декремент затухания, если сопро­тивление среды увеличить в η = 2,00 раза? Во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невоз­можны?

62. К невесомой пружине подвесили грузик, в результате чего она растянулась на Ax = 9,8 см. С каким периодом будет колебаться грузик, если ему дать небольшой толчок в вертикаль­ном направлении? Логарифмический декремент затухания λ — 3,1.

63. Найти добротность осциллятора, у которого амплитуда смещения уменьшается в η = 2,0 раза через каждые n = 110 коле­баний.

64. Частицу сместили из положения равновесия на расстоя­ние Z= 1,0 см и предоставили самой себе. Какой путь пройдет, колеблясь, эта частица до полной остановки, если логарифмиче­ский декремент затухания λ = 0,020?

65. Найти добротность математического маятника длины I = -=> 50 см,-если за промежуток времени τ = 5,2 мин его полная меха­ническая энергия уменьшилась в η = 4,0-10⁴ раз.

66. Однородный диск радиуса R = 13 см может вращаться вокруг горизонтальной оси, перпендикулярной к его плоскости и проходящей через край диска. Найти период малых колебаний этого диска, если логарифмический декремент затухания λ = 1,00.

67. Тонкий однородный диск массы т и радиуса R_f подвешен­ный в горизонтальном положении к упругой нити, совершает кру­тильные колебания, в жидкости. Момент упругих сил со стороны нити N = αφ, где α — постоянная, φ — угол поворота из положе­ния равновесия. Сила сопротивления, дей­ствующая на единицу поверхности диска, F₁ = ηι\ где η — постоянная, ν — ског рссть данного элемента диска относитель­но жидкости. Найти частоту малых коле­баний.

68. Диск А радиуса R_f подвешенный на упругой нити между двумя неподвиж­ными плоскостями (рис. 4.24), совершает крутильные колебания вокруг своей оси OO'. Момент инерции диска, относительно этой оси /, зазор между диском и каждой из плоскостей h_f причем h R. Найти вязкость газа, окружаю­щего диск A_f если период колебаний диска T и логарифмический декремент затухания λ.

69. Проводник в форме квадратной рамки со стороной а, под­вешенный на упругой нити, находится в однородном горизонталь­ном магнитном поле с индукцией В. В положении равновесия пло­скость рамки параллельна вектору В (рис. 4.25).

Будучи выведена из положения равновесия, рамка

совершает малые колебания вокруг вертикальной

оси, проходящей через ее центр. Момент инерции

рамки относительно этой оси /, ее электрическое

сопротивление R> Пренебрегая индуктивностью

рамки, найти время, через которое амплитуда ее - „

углового поворота уменьшится в е раз.

60. На горизонтальной плоскости с коэффи-

циентом трения 6=0,10 лежит брусок массы Рис. 4.25. т = 0,50 кг, соединенный горизонтальной неде- формированной пружинкой со стенкой. Жесткость пружинки κ = 2,45 Н/см, а ее масса пренебрежимо мала. Брусок сместили так, что пружинка растянулась на х₀ = 3,0 см, а затем отпустили. Найти:

а) период колебаний бруска;

б) число колебаний, которые совершит брусок до остановки.

60. 7777777777777777777777. 0

    Ά

    V////////U

    Oⁱ

    Рис. 4.24.

    Шарик массы /т? может совершать незатухающие гармони­ческие колебания около точки χ = 0 с собствелной частотой ω₀.

В момент t = 0, когда шарик находился в состоянии равновесия, к нему приложили вынуждающую силу F = F₀ cos ωί, совпадаю­щую по направлению с осью χ. Найти уравнение вынужденных ко­лебаний шарика χ (ί).

60. Частица массы т может совершать незатухающие гармо­нические колебания под действием упругой силы с коэффициен­том k. Когда частица находилась в состоянии равновесия, к ней приложили постоянную силу F_y которая действовала в течение τ се­кунд. Найти амплитуду колебаний частицы после окончания дей­ствия этой силы. Изобразить примерный график колебаний χ (ί). Исследовать возможные случаи.

61. Шарик массы т_у подвешенный к пружинке, удлиняет последнюю на величину Δ/. Под действием внешней вертикальной силы, меняющейся по гармоническому закону с амплитудой F_0y шарик совершает вынужденные колебания. Логарифмический дек­ремент затухания равен λ. Пренебрегая массой пружинки, найти круговую частоту вынуждающей силы, при которой амплитуда сме­щения шарика максимальна. Каково значение этой амплитуды?

62. Амплитуды смещений вынужденных гармонических коле­баний при частотах (o₁ = 400 рад/с и ω₂ = 600 рад/с равны между собой. Найти частоту, при которой амплитуда смещения максимальна.

63. При частотах вынуждающей гармонической силы O₁ и о>₂ амплитуда скорости частицы равна половине максимального зна­чения. Найти:

а) частоту, соответствующую резонансу скорости;

б) коэффициент затухания β и частоту затухающих колебаний ω частицы.

60. Некоторая резонансная кривая соответствует механиче­ской колебательной системе с логарифмическим декрементом зату­хания λ = 1,60. Найти для этой кривой отношение максимальной амплитуды смещения к амплитуде смещения при очень малой частоте.

61. Под действием внешней вертикальной силы F = F₀ cos ωί тело, подвешенное на пружинке, совершает установившиеся вы­нужденные колебания по закону χ = a cos (ωί — φ). Найти работу силы F за период колебания.

62. Шарик массы т = 50,0 г подвешен на невесомой пружинке жесткости κ = 20,0 Н/м. Под действием вынуждающей вертикаль­ной гармонической силы с частотой ω = 25,0 рад/с шарик совершает установившиеся колебания с амплитудой а = 1,3 см. При этом сме­щение шарика отстает по фазе от вынуждающей силы на φ = ³/₄π. Найти:

а) добротность данного осциллятора;

б) работу вынуждающей силы за период колебания.

60. Шарик массы т_у подвешенный на невесомой пружинке, может совершать вертикальные колебания с коэффициентом зату­хания β. Собственная частота колебаний равна ω₀. Под действием внешней вертикальной силы, меняющейся по закону F = F₀ cos со/, шарик совершает установившиеся гармонические колебания. Найти

а) среднюю за период колебания мощность (P) силы F\

б) частоту ω силы F_y при которой (P) максимальна; чему равна <Р)_макс?

60. Вынужденная гармоническая сила F_y частоту которой можно менять, не изменяя ее амплитуды, действует в вертикальном направлении на шарик, висящий на невесомой пружине. Коэффи­циент затухания в η раз меньше собственной частоты о>₀ колебаний шарика. На сколько процентов отличается средняя за период коле­бания мощность (P) силы F при частоте, соответствующей резонансу смещения, от максимальной средней мощности (P)_hskc этой силы?

61. Однородный горизонтальный диск, укрепленный в центре на упругом вертикальном стержне, совершает вынужденные кру­тильные колебания под действием момента сил N = AZ_mCoso)/. Колебания происходят по закону φ = (p_mcos (ω/ — α). Найти:

а) работу сил трения, действующих на диск, за период коле­бания;

б) добротность данного осциллятора, если момент инерции диска относительно его оси равен /.

4.2. Электрические колебания

Затухающие колебания контура

где

R

(4.2а)

2 L

Я=Qnfi^^{t cos} +^а)» 1

φ Логарифмический декремент затухания λ и добротность Q контура определяются формулами (4.Ir). При слабом затухании:

^λ="*/T- ^q^wVT

φ Установившиеся вынужденные колебания при последовательном вклю­чении в контур напряжения U = U_mCosat: I = I_mCOs (ω/—φ), (4.2в)

где

U

м

Im =

(4.2г)

CdL

оС

Соответствующая векторная диаграмма на­пряжений показана на рис. 4.26.

φ Мощность, выделяемая в цепи переменного тока:

P = UIcos φ, (4.2д)

где U и / — действующие (эффективные) значения напряжения и тока:

(4.26)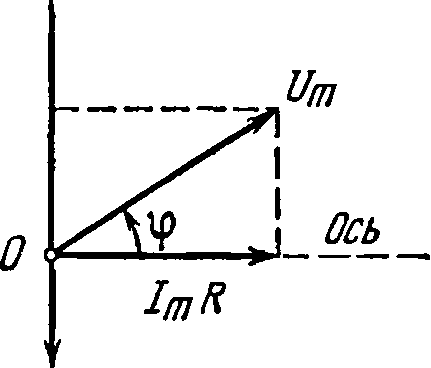

Рис. 4.26.

токов

I_mWL ''

IjtiMC

U = U_mfV 2, l = l_miV2. <4.2е)

60. Под действием некоторой причины свободные электроны в плоской медной пластине сместились на небольшое расстояние χ перпендикулярно к ее поверхности. Вследствие этого возник поверх­ностный заряд и соответствующая возвращающая сила, что привело к возбуждению так называемых плазменных колебаний. Найти круговую частоту этих .колебаний, если концентрация свободных электронов в меди η = 0,85-10²⁹ м"¹.

61. В колебательном контуре, состоящем из конденсатора ёмкости С и катушки индуктивности L, совершаются свободные незатухающие колебания, при которых амплитуда напряженно на конденсаторе равна U_m. Найти для произвольного момента-вре­мени связь между током / в контуре и напряжением.U на конденса­торе. Решить этот вопрос как с помощью закона Ома, так и энерге­тически.

62. Колебательный контур состоит из конденсатора емкости С, катушки индуктивности L с пренебрежимо малым сопротивлением и ключа. Цри разомкнутом ключе конденсатор зарядили до напря­жения U_m и затем в момент t = 0 замкнули ключ. Найти:

а) ток в контуре как функцию времени I(t)\

б) э. д. с. самоиндукции в катушке в моменты, когда электри­ческая энергия конденсатора оказывается равной энергии тока в катушке.

60. В колебательном контуре, состоящем из плоского конден­сатора и катушки индуктивности с пренебрежимо малым активным сопротивлением, происходят колебания с энергией W. Пластины конденсатора медленно раздвинули так, что частота колебаний увеличилась в η раз. Какую работу совершили при этом?

61. "В колебательном контуре (рис.. 4.27) индуктивность ка­тушки L = 2,5 мГ, а емкости конденсаторов C₁ = 2,0 мкФ и C₂ = 3,0 мкФ. Конденсаторы зарядили до напряжения U= 180 В и замкнули ключ К. Найти:

а) период собственных колебаний;

б) амплитудное значение тока через катушку.

Рис. 4.27. Рис. 4.28.

4.99. Электрическая цепь (рис. 4.28) имеет пренебрежимо малое активное сопротивление. Левый конденсатор зарядили до напряже­ния U₀ и затем — в момент /='0—"замкнули ключ К· Найти зависимость от времени t напряжений на левом и правом конден­саторах.

100. Колебательный контур состоит из катушки индуктивности L и конденсатора емкости С. Сопротивление катушки и соединитель­ных проводов пренебрежимо мало. Катушка находится в постоян­ном магнитном поле, так что суммарный поток, пронизывающий все витки катушки, равен Ф. В момент t = О магнитное поле выклю­чили. Считая время выключения очень малым по сравнению с пе­риодом собственных колебаний контура, найти ток в контуре как функцию времени t.

101. В контуре совершаются свободные затухающие колебания, при которых напряжение на конденсаторе меняется во времени по Закону U = Ucoswt. Найти моменты времени, когда модуль напряжения на конденсаторе достигает:

а) амплитудных значений;

б) максимальных (экстремальных) значений.

100. Некоторый колебательный контур содержит конденсатор емкости С, катушку с индуктивностью L и активным сопротивле­нием R₁ а также ключ. При разомкнутом ключе конденсатор заря­дили, после чего ключ замкнули, и начались колебания. Найти отношение напряжения на конденсаторе к его амплитудному значе­нию в момент непосредственно после замыкания ключа.

101. В контуре с емкостью С и индуктивностью L происходят свободные затухающие колебания, при которых ток меняется во времени по закону / — 1_те~^sinwi. Найти напряжение на кон­денсаторе в зависимости от времени и, в частности, в момент * = 0.

102. Колебательный контур состоит из конденсатора емкости С = 4,0 мкФ и катушки с индуктивностью L = 2,0 мГ и активным сопротивлением R = 10 Ом. Найти отношение энергии магнитного поля катушки к энергии электрического поля конденсатора в момент максимума тока.

103. Некоторый колебательный контур содержит две последо­вательно соединенные катушки с активными сопротивлениями R₁ и R₂ и индуктивностями L₁ и L₂, причем взаимная индуктивность их пренебрежимо мала. Эти катушки надо заменить одной так, чтобы частота и добротность контура не изменились. Найти индук­тивность и активное сопротивление такой катушки.

104. Найти время, за которое амплитуда колебаний тока в контуре с добротностью Q = 5000 уменьшится в η = 2,0 раза, если частота колебаний ν = 2,2 МГц.

105. Колебательный контур имеет емкость С = 10 мкФ, индук­тивность L = 25 мГ и активное сопротивление R= 1,0 Ом. Через сколько колебаний амплитуда тока в этом контуре уменьшится в е раз?

106. На сколько процентов отличается частота ω свободных колебаний контура с добротностью Q = 5,0 от собственной частоты CO₀ колебаний этого контура?

107. В схеме (рис. 4.29) э. д. с. элемента S = 2,0 В, его внут­реннее сопротивление г = 9,0 Ом, емкость конденсатора С = 10 мкФ,

индуктивность катушки L = 100 мГ и сопротивление R = 1,0 Ом. В некоторый момент ключ К разомкнули. Найти энергию колебаний

в контуре:

а) непосредственно после размыкания ключа;

б) через t = 0,30 с после размыкания ключа.

4.110. В контуре, добротность которого Q = 50 и собственная частота колебаний v₀ = 5,5 кГц, возбуждаются затухающие колебания. Через сколько времени энергия, запасенная в контуре, уменьшится в η = 2,0 раза?

111. Колебательный контур содержит конденсатор с утечкой. Емкость конденсатора С, его активное сопротивление R. Индуктив­ность катушки L. Сопротивление катушки и проводов пренебре­жимо мало. Найти:

а) частоту затухающих колебаний такого контура;

б) его добротность.

111. Найти добротность контура с емкостью C = 2,0 мкФ и индуктивностью L = 5,0 мГ, если на поддержание в нем незату­хающих колебаний с амплитудой напряжения на конденсаторе U_m — 1,0 В необходимо подводить мощность (P) = 0,10 мВт. Зату­хание колебаний в контуре достаточно мало.

112. Какую среднюю мощность должен потреблять колеба­тельный контур с активным сопротивлением R = 0,45 Ом, чтобы в нем поддерживались незатухающие гармонические колебания с амплитудой тока I_m = 30 мА?

113. Колебательный контур содержит конденсатор емксстью. С — 1,2 нФ и катушку с индуктивностью L = 6,0 мкГ и активным сопротивлением R = 0,50 Ом. Какую среднюю мощность нужно подводить к контуру, чтобы поддерживать в нем незатухающие гармонические колебания с амплитудой напряжения на конденса­торе U_m= 10 В?

114. 

     Рис. 4.29.

     Найти частоту затухающих колебаний контура, показан­ного на рис. 4.30. Емкость С, индуктивность L и активное сопротив­ление R предполагаются известными. Выяснить, при каком соотно­шении между С, L и R колебания возможны.

^fC

R С

I—

а)

Рис. 4.31,

Рис. 4.30.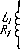

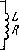
4.116. Имеются два колебательных контура (рис. 4.31) с кон­денсаторами одинаковой емкости. При каком соотношении между

индуктивностями и активными сопротивлениями катушек частоты и затухание свободных колебаний в обоих контурах будут одина­ковыми? Взаимная индуктивность катушек левого контура прене­брежимо мала.

117. Контур состоит из последовательно включенных конден­сатора емкости С, катушки индуктивности L, ключа и сопротивле­ния, равного критическому для данного контура. При разомкнутом ключе конденсатор зарядили до напряжения U₀ и в момент £ = О ключ замкнули. Найти ток I в контуре как функцию времени t. Чему равен /_макс?

118. Катушку с активным сопротивлением R и индуктивностью L подключили в момент t = 0 к источнику напряжения U = = U_mQOSiiit. Найти ток в катушке как функцию времени t.

119. Цепь, состоящую из последовательно соединенных кон­денсатора емкости С и сопротивления R, подключили к переменному напряжению U = U_mcos<ot в момент / = 0. Найти ток в цепи как функцию времени t.

120. Длинный однослойный соленоид из проволоки с удельным сопротивлением ρ имеет на единицу длины η плотно расположенных витков. Толшина изоляции провода пренебрежимо мала. Радиус сечения соленоида равен а. Найти разность фаз между током и переменным напряжением с частотой ν, которое подключено к кон­цам соленоида.

121. Концы цепи, состоящей из последовательно включенных конденсатора и активного сопротивления R = 110 Ом, подсоеди­нили к переменному напряжению с амплитудным значением U_m = = 110 В. При этом амплитуда установившегося тока в цепи I_m = ь= 0,50 А. Найти разность фаз между током и подаваемым напря­жением.

122. На рис. 4.32 показана простейшая схема сглаживающего фильтра. На левый вход подают напряжение U = U₀ (1 + cosωί). Найти:

а) выходное напряжение U'(t)\

б) значение величины RC_j при котором амплитуда переменной составляющей напряжения на выходе будет в η = 7,0 раза меньше постоянной составляющей, если ω = 314 рад/с.

R_f

LR

L_tR

/WW.

ω<ω₀

-о о- 6)

-О о-

а)

Рис. 4.33.

R

О—(	I—		—о
U	C =		и'
о—			о

Рис. 4.32.

4.123. Изобразить примерные векторные диаграммы напряжений в электрических цепях, показанных на рис. 4.33, а, б. Внешнее напряжение U предполагается гармоническим с частотой ω.

124. Цепь, состоящая из последовательно соединенных KOHⁱ денсатора емкости С = 22 мкФ и катушки с активным сопротивле^ нием R = 20 Ом и индуктивностью L = 0,35 F, подключена к сети переменного напряжения с амплитудой U_m = 180 В и частотой ω = 314 рад/с. Найти:

а) амплитуду тока в цепи;

б) разность фаз между током и внешним напряжением;

в) амплитуды напряжения на конденсаторе и катушке.

124. Цепь из последовательно соединенных конденсатора емкости С, сопротивления R и катушки с индуктивностью Lam пренебрежимо малым активным сопротивлением подключена к ге­нератору синусоидального напряжения, частоту которого можно менять при постоянной амплитуде. Найти частоту, при которой максимальна амплитуда напряжения:

а) на конденсаторе; б) на катушке.

124. Переменное напряжение с частотой ω = 314 рад/с и амплитудным значением U_m = 180 В подключено к концам цепи, состоящей из последовательно соединенных конденсатора и катушки с активным сопротивлением R = 40 Ом и индуктивностью L = = 0,36 Г. При каком значении емкости конденсатора амплитуда напряжения на катушке будет максимальной? Чему равна эта амплитуда и соответствующая амплитуда напряжения на конден­саторе?

125. Конденсатор емкости С, пространство между обкладками которого заполнено слабо проводящей средой с активным сопротив­лением R, подключили к источнику, переменного напряжения U =. U_mcosG)/. Найти установившийся ток в подводящих проводах в зависимости от времени. Сопротивление проводов пренебрежимо мало.

126. Колебательный контур содержит, конденсатор емкости С и соленоид с индуктивностью L₁. Соленоид индуктивно связан с короткозамкнутой катушкой, имеющей индуктивность L₂ и пре­небрежимо малое активное сопротивление. Коэффициент их взаим­ной индуктивности равен L₁₂. Найти собственную частоту данного колебательного контура.

127. Найти добротность колебательного контура, в который последовательно включен источник переменной э. д. е., если при резонансе напряжение на конденсаторе в η раз превышает напря­жение на источнике.

128. Цепь переменного тока, состоящая из последовательно соединенных катушки и конденсатора, подключена к источнику переменной э. д. е., причем индуктивность катушки подобрана так, что ток в цепи максимален. Найти добротность системы, если из­вестно, что при увеличении индуктивности в η раз ток в цепи умень­шается в η раз.

129. Цепь, содержащая последовательно соединенные конден­сатор и катушку с активным сопротивлением, подключена к источ­нику гармонического напряжения, частоту которого можно менять,

_не изменяя .амплитуды напряжения. При частотах ^o₁ и ω₂ ампли­туды тока оказались в η раз меньше резонансной амплитуды. Найти:

а) резонансную частоту; б) добротность цепи.

124. Показать, что при малом затухании добротность кон­тура, в котором совершаются вынужденные колебания, Q « ω₀/Δω, где ω₀ — собственная частота колебаний, Δω — ширина резонанс­ной кривой /(ω) на «высоте», в У2 раз меньшей амплитуды тока при резонансе.

125. К концам цепи, состоящей из последовательно соединен­ных конденсатора и катушки, подают два переменных напряжения одинаковой амплитуды, но разной частоты. Частота одного напря­жения равна собственной частоте (со₀), другого — в η раз больше. Найти отношение амплитуд токов (IJI)_y возбуждаемых обоими напряжениями, если добротность системы равна Q. Вычислить это отношение для Q = 10 и 100, если η ='1,10.

126. Для зарядки аккумулятора постоянным током /₀ тре­буется i₀ часов. Сколько времени понадобится для зарядки такого аккумулятора от сети через однополу- периодный выпрямитель, если действую- / щее значение тока тоже равно /₀?

127. Найти действующее значение тока, если среднее значение его равно I_0y , а сам ток зависит от времени по закону:

а) показанному на рис. 4.34; Рис. 4.34.

б) I ~ I sin ωί |.

124. Соленоид с индуктивностью L = 7 мГ и активным со­противлением R = 44 Ом подключили сначала к источнику посто­янного напряжения U_0y а затем к генератору синусоидального напряжения с действующим значением U = U₀. При какой частоте генератора мощность, потребляемая соленоидом, будет в ή = 5,0 раза меньше, чем в первом случае?

125. К сети с действующим напряжением i/ = 100 В подклю­чили катушку, индуктивное сопротивление которой X_l = 30 Ом и импеданс Z = 50 Ом. Найти разность фаз между током и напря­жением, а также тепловую мощность, выделяемую в катушке.

126. Катушка с индуктивностью L = 0,70 Г и активным со­противлением г = 20 Ом соединена последовательно с безындук­ционным сопротивлением R_y и между концами этой цепи приложено переменное напряжение с действующим значением U = 220 В и частотой ω = 314 рад/с. При каком значении сопротивления R в цепи будет выделяться максимальная тепловая мощность? Чему она равна?

4; 139. Цепь, состоящая из - последовательно соединенных кон­денсатора и катушки, подключена к сети. Изменив емкость конден­сатора, добились увеличения выделяемой тепловой'мощности "в ка­тушке BM= 1,7 раза. На сколько процентов изменилось при этом значение cos φ?

4.140. В колебательный контур с добротностью Q = 100 вклю­чены последовательно источник синусоидальной э. д. с. с постоян­ной амплитудой напряжения. При некоторой частоте внешнего напряжения тепловая мощность, выделяемая в контуре, оказывается максимальной. На сколько процентов следует изменить эту частоту, чтобы выделяемая мощность уменьшилась в η = 2,0 раза?

' 4.141. Цепь, состоящую из последовательно соединенных безын­дукционного сопротивления R = 0,16 кОм и катушки с активным сопротивлением, подключили к сети с действующим напряжением U = 220 В. Найти тепловую мощность, выделяемую на катушке, если действующие напряжения на сопротивлении R и катушке равны соответственно U₁ = 80 В и U₂ = 180 В.

142. Катушка и безындукционное сопротивление R = 25 0м подключены параллельно к сети переменного напряжения. Найти тепловую мощность, выделяемую в катушке, если из сети потреб­ляется ток I = 0,90 А, а через катушку и сопротивление R текут токи соответственно I₁ = 0,50 А и I₂ = 0,60 А.

143. Найти полное сопротивление участка цепи, состоящего из параллельно включенного конденсатора емкости C = 73 мкФ и активного сопротивления R = 100 Ом, —для переменного тока частоты со = 314 рад/с.

144. Изобразить примерные векторные диаграммы токов в электрических контурах, показанных на рис. 4.35. Предполагается,

R ..С R

I <	В А ι Q Qn ι	HH I <	В А	-C=Zb-
		LtR		L

ⁿC

α) δ) β)

Рис. 4.35.

что подаваемое между точками А и В напряжение синусоидальное и параметры каждого контура подобраны так, что суммарный ток I₀ через контур отстает по фазе от внешнего напряжения на угол φ.

142. Конденсатор емкости С = 1,0 мкФ и катушку с активным сопротивлением R = 0,10 0м и индуктивностью L= 1,0 мГ под­ключили параллельно к источнику синусоидального напряжения с действующим значением U = 31 В. Найти:

а) частоту ω, при которой наступает резонанс;

б) действующее значение подводимого тока при резонансе, а также соответствующие токи через катушку и конденсатор.

142. К источнику синусоидального напряжения с частотой ω подключили параллельно конденсатор емкости С и катушку с ак­тивным сопротивлением R и индуктивностью L. Найти разность фаз между подводимым к контуру током и напряжением на источ­нике.

143. Участок цепи состоит из параллельно включенных кон­денсатора емкости С и катушки с активным сопротивлением R и индуктивностью L. Найти полное сопротивление этого участка для переменного напряжения с частотой ω.

144. Кольцо из тонкого провода с активным сопротивлением R и индуктивностью L вращают с постоянной угловой скоростью ω во внешнем однородном магнитном поле, перпендикулярном к оси вращения. При этом поток магнитной индукции внешнего поля через кольцо изменяется во времени по закону Φ = Ф₀соз ωί. Показать, что:

^Ла) индукционный ток в кольце зависит от времени как I —

= I_m sin (ωί — φ), где I_m = ωΦο/YR*+ ω²ΖΛ причем tgcp = ωL/R;

б) средняя механическая мощность, развиваемая внешними силами для под­держания вращения, определяется фор­мулой P = У₂<о²Ф IR/(R² + ω² L²).

142. На деревянный сердечник (рис. 4.36) надеты две катушки: ка­тушка 1 с индуктивностью L₁ и замкну­тая накоротко катушка 2 с активным сопротивлением R и индуктивностью L₂. Взаимная индуктивность катушек зависит от расстояния χ между ними по закону L₁₂(x). Найти среднее по времени значение силы взаимодействия между катушками, когда по катушке 1 течет пере­менный ток I₁ — Iq cos ωί.

4.3. Упругие вопны. Акустика

φ Уравнения плоской и сферической воли:

ξ=α cos(tot—kx), £=y-cos (Ы—kr). (4.3а)

Для однородной поглощающей среды в эти формулы входит множитель соот­ветственно e~Y* и e~Y^r, где γ — коэффициент затухания волны.

φ Волновое уравнение:

^4-^4-^1 = 1¾ агв)

дх® "^r^y* "^rAz^a Φ dt*' ■ " ⁷

φ Фазовая скорость продольных волн в упругой среде и поперечных волн в струне (^₁):

V_i=VEft. V_l=YtJ^. (4.3b)

где E—модуль Юнга, р —плотность среды, T — натяжение струны, P₁-ее линейная плотность.

φ Объемная плотность энергии упругой волны:

w=ρα²ω² Sin² (ωί—kx), (w) =¹I₂QaW. (4.3г)

φ Плотность потока энергии — вектор Умова:

Рис. 4.36.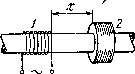

J=Stwv_e <J> =VafKAa²V. (4,3д)

φ Уравнение стоячей волны:

ξ = a cos kx · cos ωί. {4.3e)

φ Акустический эффект Доплера:

^ϋ ^HCT

Φ Уровень громкости звука (в белах):

L = Ig (///₀). (4.3з)

Φ Связь между интенсивностью / звуковой волны и амплитудой колебания давления (Ap)_m:

/ = (Ap)J_l^pcr. (4.3н)

142. За сколько времени звуковые колебания пройдут расстоя­ние / между точками А и B₉ если температура воздуха между ними

меняется линейно от T₁ до Скорость звука в воздухе ν = где α — постоянная.

142. Плоская гармоническая волна с частотой ω распрост­раняется со скоростью ν в направлении, составляющем углы а, β, γ с осями X₉ у, г. Найти разность фаз колебаний в точках среды с координатами x_l9 y_l9 Z₁ и X₂₉ у₂₉ Z₂.

143. Плоская волна с частотой ω распространяется так, что некоторая фаза колебаний перемещается вдоль осей х₉ у, ζ со ско­ростями соответственно v_l9 V₂₉ Найти волновой вектор к, пред­полагая орты осей координат е*, е_у9 е₂ заданными.

144. В среде К распространяется упругая плоская волна ξ = = a cos(git — kx). Найти уравнение этой волны в /('-системе отсчета, движущейся в положительном направлении оси χ с постоянной скоростью V по отношению к среде /С. Исследовать полученное выражение.

145. Показать, что любая дифференцируемая функция f(t + + αχ), где α — постоянная, является решением волнового уравне­ния. Каков физический смысл постоянной а?

146. Уравнение бегущей плоской звуковой волны имеет вид I = 60 cos (1800* — 5,3х), где ξ в микрометрах, t в секундах, χ в метрах. Найти:

а) отношение амплитуды смещения частиц среды к длине волны;

б) амплитуду колебаний скорости частиц среды и ее отношение к скорости распространения волны;

в) амплитуду колебаний относительной деформации среды и ее связь с амплитудой колебания скорости частиц среды.

142. В однородной упругой среде распространяется плоская волна вида ξ = a cos (ωί — kx). Изобразить для. момента t = 0:

а) графики зависимостей от χ величин ξ, dg/dt и dl/dx;

б) направление скорости частиц среды в точках, где ξ = 0, для случаев продольной и поперечной волн;

в) примерный график распределения плотности среды р(х) для продольной волны.

4.157· В однородной среде распространяется плоская упругая волна вида ξ = а cos (ω/ — kx), где α, γ, ω и k — постоянные. Найти разность фаз колебаний в точках, где амплитуды смещения частиц среды отличаются друг от друга на η = 1,0%, если γ =

0,42 м'¹ и длина волны λ = 50 см.

158. Найти радиус-вектор, характеризующий положение то­чечного источника сферических волн, если известно, что этот источ­ник находится на прямой между точками с радиус-векторами T₁ и г₂, в которых амплитуды колебаний частиц среды равны и а₂. Затуха- нйе волны пренебрежимо мало, среда однородная.

159. Точечный изотропный источник испускает звуковые коле­бания с частотой ν = 1,45 кГц. На расстоянии г₀ = 5,0 м от источ­ника амплитуда смещения частиц среды а₀ = 50 мкм, а в точке A₉ находящейся на расстоянии г = 10,0 м от источника, амплитуда смещения в η = 3,0 раза меньше а₀. Найти:

а) коэффициент затухания волны γ;

б) амплитуду колебаний скорости частиц среды в точке Л.

158. В упругой однородной среде распространяются две плос­кие волны, одна — вдоль оси X₉ другая — вдоль оси у: I_i

= a cos (e>t — kx), I₂ — ^{а cos} — ky). Найти характер движения частиц среды в плоскости ху, если обе волны:

а) поперечные и направление колебаний одинаково;

б) продольные.

158. В среде распространяется незатухающая плоская гармо­ническая волна. Найти среднюю объемную плотность полной энер­гии колебаний (w)₉ если в любой точке среды объемная плотность энергии равна W₀ через одну шестую периода колебаний после про­хождения максимума смещения.

159. Точечный изотропный источник звука находится на пер­пендикуляре к плоскости кольца, проходящем через его центр О. Расстояние между точкой О и источником I= 1,00 м, радиус кольца R = 0,50 м. Найти средний поток энергии через площадь, ограни­ченную кольцом, если в точке О интенсивность звука I_ij = 30 мкВт/м². Затухание волн пренебрежимо мало.

160. Изотропный точечный источник, звуковая мощность которого P = 0,10 Вт, находится в центре круглого полого цилиндра радиуса R= 1,0 м и высоты h = 2,0 м. Полагая, что стенки цилин­дра полностью поглощают звук, найти средний поток энергии, падающий на боковую поверхность цилиндра.

161. В однородной упругой среде установилась плоская стоя­чая волна вида ξ = α cos kx-cos ωί. Изобразить:

а) графики зависимостей от χ величин ξ и д^/дх в моменты t = 0 и t = Т/2, где T — период колебаний;

б) графики распределения плотности среды р(х) для продольных колебаний в моменты t = 0 и t -- Т/2;

в) график распределения скоростей частиц среды β момент t — Т/4; указать направления скоростей в этот моментъ пучностях— для продольных и поперечных колебаний.

158. В однородной среде с плотностью ρ установилась про­дольная стоячая волна вида ξ = a cos fct-cos со/. Найти выражения для объемной плотности:

а) потенциальной энергии w_p (χ, t)\

б) кинетической энергии w_k (χ, t).

Изобразить графики распределения объемной плотности полной энергии w в пределах между двумя соседними узлами смещения в моменты t = 0 и t = Т/4, где T — период колебаний.

158. На струне длины 120 см образовалась стоячая волна, причем точки струны, для которых амплитуда смещения равна 3,5 мм, отстоят друг от друга на 15,0 см. Найти максимальную амплитуду смещения. Какому обертону соответствуют эти коле­бания?

159. Найти отношение частот основного тона двух одинаковых струн после того, как одну из них растянули на Tj₁ = 2,0%, а дру­гую — на η₂ = 4,0%. Натяжение считать пропорциональным рас­тяжению.

160. Определить, как и во сколько раз изменится частота основ­ного тона натянутой струны, если ее длину укоротить на 35%, а натяжение увеличить на 70%.

161. Для определения скорости звука в воздухе методом акус­тического резонанса используется труба с поршнем и звуковой мембраной, закрывающей один из ее торцов. Найти скорость звука, если расстояние между соседними положениями поршня, при кото­рых наблюдается резонанс на частоте ν = 2000 Гц, составляет / — 8,5 см.

162. Найти число возможных собственных колебаний столба воздуха в трубе, частоты которых меньше V₀ = 1250 Гц. Длина трубы I = 85 см. Скорость звука ν = 340 м/с. Рассмотреть два случая:

а) труба закрыта с одного конца;

б) труба открыта с обоих концов.

Считать, что открытые концы трубы являются пучностями смещения.

158. Медный стержень длины J = 50 см закреплен в середине. Найти число продольных собственных колебаний этого стержня в диапазоне частот от 20 до 50 кГц. Каковы их частоты?

159. Струна массы т закреплена с обоих концов. В ней возбу­дили колебания основного тона с круговой частотой ω и максималь­ной амплитудой смещения а_Мак_С· Найти:

а) максимальную кинетическую энергию струны;

б) среднюю за период колебания кинетическую энергию струны.

158. В однородном стержне, площадь сечения которого S и плотность р, установилась стоячая волна вида ξ = a sin kx-cos ω/. Найти полную механическую энергию, заключенную между сече­ниями, которые проходят через соседние узлы смещения.

159. Источник звуковых колебаний частоты V₀ = 1000 Гц движется по нормали к стенке со скоростью и = 0,17 м/с. На этой же нормали расположены два неподвижных приемника Il₁ и #₂, причем последовательность расположения этих приемников и источ­ника И такая: IJ₁ — И Я₂ — стенка. Какой приемник регистри­рует биения и какова их частота? Скорость звука ν=340 м/с.

160. Неподвижный наблюдатель воспринимает звуковые коле­бания от двух камертонов, один из которых приближается, а дру­гой — с такой же скоростью удаляется. При этом наблюдатель слышит биения с частотой ν = 2,0 Гц. Найти скорость каждого камертона, если их частота колебаний V₀ = 680 Гц и скорость звука в воздухе ν = 340 м/с*

161. На оси χ находятся приемник и источник звуковых коле­баний с частотой v₀ = 2000 Гц. Источник совершает гармонические колебания вдоль этой оси с круговой частотой ω и амплитудой а = 50 см. При каком значении ω ширина частотного интервала* воспринимаемого неподвижным приемником, будет составлять Δν= = 200 Гц? Скорость звука ν = 340 м/с.

162. Источник звуковых колебаний с частотой V₀ = 1700 Гц и приемник находятся в одной точке. В момент t = 0 источник начинает удаляться от приемника с постоянным ускорением w = = 10,0 м/с². Считая скорость звука ν = 340 м/с, найти частоту колебаний, воспринимаемых неподвижным приемником через t = = 10,0 с после начала движения источника.

163. Источник звука, собственная частота которого V₀= 1,8 кГц, движется равномерно по прямой, отстоящей от неподвижного наблю­дателя на I = 250 м. Скорость источника составляет η = 0,80 скорости звука. Найти:

а) частоту звука, воспринимаемую наблюдателем в момент, когда источник окажется напротив него;

б) расстояние между источником и наблюдателем в момент, когда воспринимаемая наблюдателем частота ν = ν₀.

158. Неподвижный источник испускает монохроматический звук. К нему приближается стенка со скоростью и = 33 см/с. Скорость распространения звука в среде ν = 330 м/с. Как и на сколько процентов изменяется длина волны звука при отражении от стенки?

159. На одной и той же нормали к стенке находятся источник звуковых колебаний с частотой V₀ = 1700 Гц и приемник. Источник и приемник неподвижны, а стенка удаляется от источника со ско­ростью и = 6,0 см/с. Найти частоту биений, которую будет реги­стрировать приемник. Скорость звука υ = 340 м/с.

160. Найти коэффициент затухания у звуковой волны, если на расстояниях r_x = 10 м и г₂ = 20 м от точечного изотропного источника звука значения интенсивности звуковой волны отли­чаются друг от друга в η = 4,5 раза.

161. Плоская звуковая волна распространяется вдоль оси χ. Коэффициент затухания волны γ = 0,0230 м'¹. В точке χ = 0 уровень громкости L = 60 дБ. Найти:

а) уровень громкости в точке с координатой χ = 50 м;

б) координату χ точки, в которой звук уже не слышен·

158. На расстоянии г₀ — 20,0 м от точечного изотропного источника звука уровень громкости jL₀ = 30,0 дБ. Пренебрегая затуханием звуковой волны, найти: ^

а) уровень громкости на расстоянии г ==. 10,0 м οτ источника;

б) расстояние от источника, на котором звук неслышен. .

158. Наблюдатель A_y находящийся на некотором расстоянии от звучащего камертона, отметил исчезновение звука на τ = 23 с раньше, чем наблюдатель B_y находящийся в η = 5,0 раза ближе к камертону. Найти коэффициент затухания β колебаний камертона. Затухание звуковых волн в среде пренебрежимо мало.

159. В среде с плотностью ρ распространяется плоская пр**- дольная гармоническая волна. Скорость волны равна и. Считая изменение плотности среды при прохождении волны. Δ ρ ρ, показать, что:

а) приращение давления в среде Δρ = — pv²(dl/dx)_y где δξ/дх — относительная деформация;

б) интенсивность волны определяется формулой (4.3и).

158. На пути плоской звуковой волны, распространяющейся в воздухе, находится шар радиуса R = 50 см. Длина звуковой волны λ = 20 см, частота ν = 1700 Гц, амплитуда колебаний давле­ния в воздухе (Ap)_m = 3,5 Па. Найти средний за период колебания поток энергии, падающей на поверхность „шара.

159. Точка А находится на расстоянии г = 1,5 м от точечного изотропного источника звука частоты ν = 600 Гц. Звуковая мощ­ность источника P = 0,80 Вт. Пренебрегая затуханием волн и считая скорость зрука в воздухе υ = 340 м/с, найти для точки А:

а) амплитуду колебаний давления (Ap)_m и ее отношение к дав­лению воздуха;

б) амплитуду колебаний частиц среды; сравнить ее с длиной волны звука.

158. На расстоянии г = 100 м от точечного изотропного источника звука частоты 200 Гц уровень громкости L = 50 дБ. Порог слышимости на этой частоте соответствует интенсивности звука I_q = 0,10нВт/м². Коэффициент затухания звуковой волны у = 5,0 м"¹. Найти звуковую мощность источника.

4.4. Электромагнитные волны. Излучение

φ Фазовая скорость электромагнитной волны:

V^dYг\I, где c^l/^ejjjv

φ В бегущей электромагнитной волне:

E V^rSi=Я V\4h^m

φ Объемная плотность энергии электромагнитного поля:

ED , BH

^Юв-2-+Т·

φ Плотность потока электромагнитной энергии —вектор Пойнтинга:

(4.4а) (4.46)

(4.4в)

S = [EH]. (4.4г)

Плотность потока энергии излучения диполя в волновой зоне:

(4.4д)

1

sin² θ,

_гз

где г —расстояние от диполя, θ— угол между раднус-вектором г и осью диполя.

φ Мощности излучения диполя с электрическим моментом ρ (t) и заряда q_t движущегося с ускорением w:

P =

P =

(4.4е)

4Л;80 3с*

1 2 о² ~ \ Zq²W²

2р^

4πε₀ Зс³

158. Электромагнитная волна с частотой ν= 3,0 МГц пере­ходит из вакуума в немагнитную среду с диэлектрической проницае­мостью ε = 4,0. Найти приращение ее длины волны.

159. Плоская электромагнитная волна падает нормально на поверхность плоскопараллельного слоя толщины I из немагнитного вещества, диэлектрическая проницаемость которого экспоненциально падает от значения E₁ на передней поверхности до ε₂ — на задней. Найти время распространения данной фазы волны через этот слой.

160. Плоская электромагнитная волна с частотой ν = 10 МГц распространяется в слабо проводящей среде с удельной проводимо­стью σ = 10мСм/м и диэлектрической проницаемостью ε = 9. Найти отношение амплитуд плотностей токов проводимости и смещения.

161. Плоская электромагнитная волна E = E_w cos(coi — кг) рас­пространяется в вакууме. Считая векторы E_m и к известными, найти вектор H как функцию времени t в точке с радиус-вектором г = 0.

162. у

     В вакууме распространяется .плоская электромагнитная

волна E = E_m cos (со/ — kr), где E_m = E_me_yt k = ke_xt е_х, е

орты осей x_t у. Найти вектор H в точке с радиус-вектором г = хе_х в момент: a) t = 0; б) t = Рассмотреть случай, когда E_m =■ 160 В/м, k = 0,51 м"¹, χ = 7,7 м и t₀ = 33 не.

4.194. Плоская электромагнитная волна E = E_mCos(ωί— kx)_t распространяющаяся в вакууме, наводит э. д. с. индукции в квадратном контуре со стороной L Расположение контура показано на рис. 4.37. Найти <?_инд(0> если E_m — 50 мВ/м, частота ν = = 100 МГц и I = 50 см.

υ

Рис. 4.38.

х

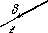
4.195. Исходя из уравнений Максвелла, показать, что для плос­кой электромагнитной волны (рис. 4.38), распространяющейся

в вакууме,

dt ^c^ дх^$ dt — дх ·

196. Найти средний вектор Пойнтинга (S) у плоской электро­магнитной волны E = Е_тсо$(ωί — кг), если волна распростра­няется в вакууме.

197. Плоская гармоническая линейно поляризованная элек­тромагнитная волна распространяется в вакууме. Амплитуда напря­женности электрической составляющей волны E_m = 50 мВ/м, час­тота ν = 100 МГц. Найти:

а) действующее значение плотности тока смещения;

б) среднюю за период колебания плотность потока энергии.

196. Шар радиуса R = 50 см находится в немагнитной среде с диэлектрической проницаемостью ε = 4,0. В среде распростра­няется плоская электромагнитная волна, амплитуда напряженности электрической составляющей которой E_m = 200 В/м. Какая энер­гия падает на шар за время t = 1,0 мин?

197. В вакууме в направлении оси χ установилась стоячая электромагнитная волна, электрическая составляющая которой E = E_mcos fex-cos ωί. Найти магнитную составляющую волны В {x_tt). Изобразить примерную картину распределения электрической и магнитной составляющих волны (Е и В) в моменты t = 0 и t = Tj4, где T — период колебаний.

198. В вакууме вдоль оси χ установилась стоячая электро­магнитная волна E = E_mcosfct-cos со£. Найти л:-проекцию век­тора Пойнтинга S^jt, t) и ее среднее за период колебаний значение.

199. Плоский воздушный конденсатор, обкладки которого имеют форму дисков радиуса R = 6,0 см, подключен к переменному синусоидальному напряжению частоты ω = 1000 рад/с. Найти отно­шение амплитудных значений магнитной и электрической энергий внутри конденсатора.

200. Переменный синусоидальный ток частоты ω = 1000 рад/с течет по обмотке прямого соленоида, радиус сечения которого R = 6,0 см. Найти отношение амплитудных значений электрической и магнитной энергий внутри соленоида.

201. Плоский конденсатор с круглыми параллельными пласти­нами медленно заряжают. Показать, что поток вектора Пойнтинга через боковую поверхность конденсатора равен приращению энергии конденсатора за единицу времени. Рассеянием поля на краях при расчете пренебречь.

202. По прямому проводнику круглого сечения течет ток /. Найти поток вектора Пойнтинга через боковую поверхность участка данного проводника, имеющего сопротивление /?.

203. Нерелятивистские протоны, ускоренные разностью по­тенциалов U₉ образуют пучок круглого сечения с током /. Найти модуль и направление вектора Пойнтинга вне пучка на расстоянии г от его оси.

204. Ток, протекающий по обмотке длинного прямого солено­ида, достаточно медленно увеличивают. Показать, что скорость возрастания энергии магнитного поля в соленоиде равна потоку вектора Пойнтинга через его боковую поверхность.

205. На рис. 4.39 показан участок двухпроводной линии пере­дачи постоянного тока, направление которого отмечено стрелками. Имея в виду, что потенциал φ₂ > φι, уста­новить с помощью вектора Пойнтинга, где /

сопротивлением. Потребляемый ток равен /.

Найти поток энергии через поперечное сечение кабеля. Внешняя проводящая оболочка кабеля предполагается тонкостенной.

196. Генератор переменного напряжения U = U₀ cos ωί пере­дает энергию потребителю по длинному прямому коаксиальному кабелю с пренебрежимо малым активным сопротивлением. Ток в цепи меняется по закону I = /_Ocos (ωί — φ). Найти средний по времени поток энергии через поперечное сечение кабеля. Внешняя оболочка кабеля тонкостенная.

197. Показать, что на границе раздела двух сред нормальные со­ставляющие вектора Пойнтинга не терпят разрыва, т. е. S_ln = S_2n.

198. Доказать, что у замкнутой системы заряженных нереля­тивистских частиц с одинаковым удельным зарядом дипольное излу­чение отсутствует.

199. Найти среднюю мощность излучения электрона, совер­шающего гармонические колебания с амплитудой а=0,10нм и частотой ω = G_jS-IO¹⁴PaVc.

200. Найти мощность излучения нерелятивистской частицы с зарядом е и массой /тг, движущейся по круговой орбите радиуса R в поле неподвижного точечного заряда q.

201. Частица с зарядом е и массой т пролетает с нереляти­вистской скоростью ν на расстоянии b от неподвижной частицы с зарядом q. Пренебрегая искривлением траектории движущейся частицы, найти энергию, теряемую этой частицей на излучение за все время пролета.

202. Нерелятивистский протон влетел по нормали в полу­пространство с поперечным однородным магнитным полем, индук­ция которого B = 1,0 Т. Найти отношение энергии, потерянной протоном на излучение за время движения в поле, к его первоначаль­ной кинетической энергии.

203. Нерелятивистская заряженная частица движется в по­перечном однородном магнитном поле с индукцией 5. Найти закон убывания (за счет излучения) кинетической энергии частицы во времени. Через сколько времени ее кинетическая энергия умень­шается в е раз? Вычислить это время для электрона и протона.

4.217. Заряженная частица движется вдоль оси у по закону у = a cos ωί, а точка наблюдения P находится на оси χ на расстоянии I от частицы (/ а). Найти отношение плотностей потока электро­магнитного излучения SifS₂ в точке P в моменты, когда координата частицы ух = 0 и у₂ = а. Вычислить это отношение, если ω = = 3,3-10⁶ рад/с и / = 190 м.

• 4.218. Заряженная частица движется равномерно со скоростью ν по окружности радиуса R_f лежащей в плоскости ху (рис. 4.40).

На оси χ в точке Р, которая от­стоит от центра окружности на расстояние, значительно превы-

· · P шающее R_f находится наблюда-

° χ тель. Найти:

а) связь между наблюдаемыми значениями у-проекции ускорения частицы и ее «/-координаты;

б) отношение плотностей потока электромагнитного излучения S₁/S₂

в точке P в моменты времени, когда частица для наблюдателя P движется к нему и от него, как показано на рисунке.

219. Электромагнитная волна, излучаемая элементарным ди­полем, распространяется в вакууме так, что в волновой зоне на луче, перпендикулярном к оси диполя, на расстоянии г от него, среднее значение плотности потока энергии равно S₀. Найти сред­нюю мощность излучения диполя.

220. Средняя мощность, излучаемая элементарным диполем, равна P₀. Найти среднюю объемную плотность энергии электро­магнитного поля в вакууме в волновой зоне на луче, перпендику­лярном к оси диполя, на расстоянии г от него.

221. Постоянный по модулю электрический диполь с моментом ρ вращают с постоянной угловой скоростью ω вокруг оси, перпен­дикулярной к оси диполя и проходящей через его середину. Найти мощность излучения такого диполя.

222. Свободный электрон находится в поле плоской электро­магнитной волны. Пренебрегая влиянием на его движение магнит­ной составляющей волны, найти отношение средней энергии, излу­чаемой осциллирующим электроном в единицу времени, к среднему значению плотности потока энергии падающей волны.

223. Плоская электромагнитная волна с частотой ω падает на упруго связанный электрон, собственная частота которого ω₀. Пренебрегая затуханием колебаний, найти отношение средней энергии, рассеянной электроном в единицу времени, к среднему значению плотности потока энергии падающей ролны.

224. 

     Считая, что частица имеет форму шарика и поглощает весь падающий на нее свет, найти радиус частицы, при котором гравитационное притяжение ее к Солнцу будет компенсироваться силой светового давления. Мощность светового излучения Солнца P = 4-IO²⁶ Вт, плотность частицы ρ = 1,0 г/см³.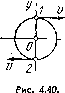

Ч а с τ ь 5

ОПТИКА

5.1. Фотометрия и геометрическая оптика

SJ

-

Λ

A ~ffi мВт/лм для K=0,555мкм

—

ν

\

\

>

1

\

I

-

-

*

•

■

(

-

φ Кривая относительной спектральной чувствительности глаза V (λ) пока­зана на рнс. 5.1.

V

1,0

Ofi Ofi

OA

O_jZ О

Л, мнм

Рис. 5.1,

Сила света / и освещенность E:

г*Ф ^Фпад

4Ω ¹ dS *

Освещенность, создаваемая точечным изотропным источником:

(5.1а)

(5.16)

_р / cos α

где а —угол между нормалью к поверхности и направлением на источник. φ Светимость M и яркость L:

M = ^d^_t L ^άΦ

dS ⁹ ~ dQ AS cos d *

Для ламбертовского источника L==Const и светимость:

(5.1 в)

(5. Ir) 189

M = JiL.

φ Связь между преломляющим углом θ призмы и углом а наименьшего отклонения:

<5Лд)

. θ

. α+θ

(S-Ie)

Рис. 5.2.

sm 2 ^{= п sin} ~2 '

где л —показатель преломления призмы. φ Формула сферического зеркала:

1 + 1-1

где R — радиус кривизны зеркала.

® Hx

У

Формулы центрированной оптической системы (рис. 5.2):

Tt Tt -и

γ = Ф,

S S

(51ж)

7 +T^essl' **'^=η'·

Соотношения между фокусными расстояниями и оптической силой:

f ~ п'

η

(5.1з)

' Φ' '

Оптическая сила сферической преломляющей поверхности:

Φ =

Tl^f — η

(5.1н)

Оптическая сила тонкой линзы в среде с показателем преломления п₀:

^Φ = <"-"<·>(^ίζ), (5.1к)

где л —показатель преломления линзы.

φ Оптическая сила толстой линзы толщины d:

Φ = Φι + Φ₂ — — ΦιΦ₂. (5.1л)

Рис. 5.3.

/Z

(5.1м)

Эта формула справедлива и для системы из двух тонких лииз, между которыми нахо­дится среда с показателем преломления п. φ Главные плоскости Я и Я' отстоят от вершин О и O^t поверхностей толстой линзы (рис. 5.3) на расстояниях:

η Φ ⁹ η Φ ·

φ Инвариант Лагранжа-—Гельмгольца:

пуи = const. (5.1н)

φ Увеличение оптического прибора:

где ψ и ψ—угловые размеры предмета при наблюдении через прибор и без него (в случае лупы и микроскопа угол ψ соответствует наблюдению на расстоянии наилучшего зрения Z₀=25 см).

1. Найти с помощью кривой относительной спектральной чув­ствительности глаза (см. рис. 5.1):

а) поток энергии, соответствующий световому потоку в 1,0 лм с длиной волны 0,51 и 0,64 мкм;

б) световой поток, приходящийся на интервал длин волн от 0,58 до 0,63 мкм, если соответствующий поток энергии Ф₉ = 4,5 мВт, причем последний распределен равномерно по всем длинам волн этого интервала. Считать, что в данном спектральном интервале функция ν(λ) зависит линейно от длины волны.

2. Точечный изотропный источник испускает световой поток Φ = 10 лм с длиной волны λ = 0,59 мкм. Найти амплитудные зна­чения напряженностей электрического и магнитного полей этого светового потока на расстоянии г = 1,0 м от источника. Восполь­зоваться кривой, приведенной на рис. 5.1.

3. Найти среднюю освещенность облучаемой части непрозрач­ной сферы, если на нее падает:

а) параллельный световой поток, создающий в точке нормального падения освещенность Е₀\

б) свет от точечного изотропного источника, находящегося на расстоянии I = 100 см от центра сферы; радиус сферы R = 60 см и сила света / = 36 кд.

4. Определить светимость поверхности, яркость которой зави­сит от направления по закону L = L₀ cos θ, где д — угол между направлением излучения и нормалью к поверхности.

5. Некоторая светящаяся поверхность подчиняется закону Ламберта. Ее яркость равна L. Найти:

а) световой поток, излучаемый элементом Δ5 этой поверхности внутрь конуса, ось которого нормальна к данному элементу, если угол полураствора конуса равен ⁱO;

б) светимость такого источника.

6. Над центром круглого стола радиуса R — 1,0 м подвешен светильник в виде плоского горизонтального диска площадью S= 100 см². Яркость светильника не зависит от направления и равна L= 1,6-10⁴ кд/м². На какой высоте от поверхности стола надо поместить светильник, чтобы освещенность периферийных точек стола была максимальной? Какова будет эта освещенность?

7. На высоте h = 1,0 м над центром круглого стола радиуса R — 1,0 м подвешен точечный источник, сила света которого I так зависит от направления, что освещенность всех точек стола оказы­вается равномерной. Найти вид функции /(θ), где θ — угол между направлением излучения и вертикалью, а также световой поток, падающий на стол, если /(0) = Z₀ = 100 кд.

8. Вертикальный луч проектора освещает центр потолка круг­лой комнаты радиуса R = 2,0 м. При этом на потолке образуется зайчик площадью 5 = 100 см². Освещенность зайчика E = 1000 л к. Коэффициент отражения потолка ρ = 0,80. Найти наибольшую освещенность стены, создаваемую светом, отраженным от потолка. Считать, что отражение происходит по закону Ламберта.

9. Равномерно светящийся купол, имеющий вид полусфера, опирается на горизонтальную поверхность. Определить освещен­ность в центре этой поверхности, если яркость купола равна L и не зависит от направления.

10. Ламбертовский источник имеет вид бесконечной плоскости. Его яркость равна L. Найти освещенность площадки, расположен­ной параллельно данному источнику.

11. Над столом находится светильник — плоский горизон­тальный диск радиуса R = 25 см. Расстояние от него до поверх­ности стола h = 75 см. Освещенность стола под центром светиль­ника E₀ = 70 лк. Найти светимость этого источника, считая его ламбертовским.

12. Светильник, имеющий вид равномерно светящейся сферы радиуса R = 6,0 см, находится на расстоянии h = 3,0 м от пола. Яркость светильника L = 2,0-10⁴ кд/м² и не зависит от направле­ния. Найти освещенность пола непосредственно под светильником.

13. Записать в векторном виде закон отражения светового луча от зеркала — через направляющие орты е и е' падающего и отраженного лучей и орт π внешней нормали к поверхности зеркала.

14. Показать, что луч света, последовательно отразившийся от трех взаимно перпендикулярных плоских зеркал, изменит свое направление на прямо противоположное.

15. При каком значении угла падения O₁ луч, отраженный от поверхности воды, будет перпендикулярен к преломленному лучу?

16. Имеются две оптические среды с плоской границей раздела. Пусть θ_1πρ — предельный угол падения луча, a O₁ — угол падения, при котором преломленный луч перпендикулярен к отраженному (предполагается, что луч идет из оптически более плотной среды). Найти относительный показатель преломления этих сред, если sin ft_lnp/sin O₁ = η = 1,28.

17. Луч света падает на плоскопараллельную стеклянную пластину толщиной d = 6,0 см. Угол падения θ = 60°. Найти вели­чину бокового смещения луча, прошедшего через эту пластину.

18. На краю бассейна стоит человек и наблюдает камень, лежащий на дне. Глубина бассейна равна /г. На каком расстоянии от поверхности воды видно изображение камня, если луч зрения составляет с нормалью к поверхности воды угол θ?

19. Показать, что при преломлении в призме с малым прелом­ляющим углом θ луч отклоняется на угол α ж (η— 1)θ независимо от угла падения, если последний также мал.

20. Луч света проходит через призму с преломляющим углом θ и показателем преломления я. Пусть α — угол отклонения луча. Показать, что при симметричном ходе луча через призму:

а) угол α минимален;

б) связь между углами α и θ определяется формулой (5.1д).

21. Для некоторой стеклянной призмы угол наименьшего отклонения луча равен преломляющему углу призмы. Найти последний.

22. Найти пределы, в которых может меняться угол отклоне­ния луча при прохождении стеклянной призмы с преломляющим углом θ '== 60°.

5.23УТрехгранная призма с преломляющим углом 60° дает угол наименьшего отклонения в воздухе 37°. Какой угол наименьшего отклонения даст эта призма в воде?

24. Луч света, содержащий две монохроматические составляю­щие, проходит через трехгранную призму с преломляющим углом θ = 60°. Определить угол Δα между обеими составляющими луча после призмы, если показатели преломления для них равны 1,515 и 1,520 и призма ориентирована на угол наименьшего отклонения.

25. Вывести с помощью принципа Ферма законы отражения

и преломления света на плоской границе раздела двух сред,

°^{7 0}^

о)

Рис. 5.4.

24. Найти построением:

а) ход луча после отражения в вогнутом и выпуклом сферичес­ких зеркалах^ (рис. 5.4, где F — фокус, OO^f — оптическая ось);

б) положение зеркала й его фокуса для случаев, показанных на рис. 5.5, где P и P^t —сопряженные точки.

Рис. 5.5.

24. Определить фокусное расстояние вогнутого зеркала, если:

а) при расстоянии между предметом и изображением / == 15 см

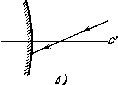
193

поперечное увеличение β = —2,0;

7 И. Е. Иродов

б) при одном положении предмета поперечное увеличение P₁ = —Ο,δΟ, а при другом положении, смещенном относительно первого на расстояние / = 5,0 см, поперечное увеличение β₂ = = —0,25.

24. Точечный источник, сила света которого I₀ = 100 кд, помещен на расстоянии s — 20,0 см от вершины вогнутого зеркала с фокусным расстоянием f = 25,0 см. Определить силу света в отра­женном пучке, если коэффициент отражения зеркала ρ = 0,80.

25. Вывести с помощью принципа Ферма формулу преломле­ния параксиальных лучей на сферической поверхности радиуса

разделяющей среды с показателями прелом­ления η и п\

24. Параллельный пучок света падает из вакуума на поверхность, которая ограни­чивает область с показателем преломления η (рис. 5.6). Найти форму этой поверх­ности — уравнение χ (г), при которой пучок будет сфокусирован в точке F на расстоянии f от вершины О. Пучок какого максимального радиуса сечения может быть сфокусирован?

25. Точечный источник расположен на расстоянии 20 см от передней поверхности стеклянной симметричной двояковыпуклой

линзы. Толщина линзы равна 5,0 см, радиус кривизны поверхностей 5,0 см. На каком расстоянии от задней поверхности этой линзы образуется изображение источника?

24. Перед выпуклой поверхностью стеклянной выпукло-плос­кой линзы толщины d = 9,0 см находится предмет. Изображение этого предмета образуется на плоской поверхности линзы, которая

• служит экраном. Определить:

а) поперечное увеличение, если радиус кривизны выпуклой поверхности линзы R = 2,5 см;

б) освещенность изображения, если яркость предмета L = = 7700 кд/м² и диаметр входного отверешя выпуклой поверхности линзы D = 5,0 мм; потери света пренебрежимо малы.

24. Найти оптическую силу и фокусные расстояния:

а) тонкой стеклянной линзы в жидкости с показателем преломле­ния п₀ = 1,7, если ее оптическая сила в воздухе Ф₀ = —5,0дп;

б) тонкой симметричной двояковыпуклой стеклянной линзы, с одной стороны которой находится воздух, а с другой — вода, если оптическая сила этой линзы в воздухе Ф₀ = + 10 дп.

24. Найти построением:

а) ход луча за собирающей и рассеивающей тонкими линзами (рис. 5.7, где OO' — оптическая ось, FuF' — передний и задний фокусы);

Рис. 5.6₃

б) положение тонкой линзы и ее фокусов, если известно положе­ние оптической оси OO^r и положение пары сопряженных точек PP^f (см. рис. 5.5); среды по обе стороны линз одинаковы;

в) ход луча 2 за собирающей и рассеивающей тонкими линзами (рис. 5.8), если известно положение линзы и ее оптической оси OO' и ход луча 1\ среды по обе стороны линз одинаковы.

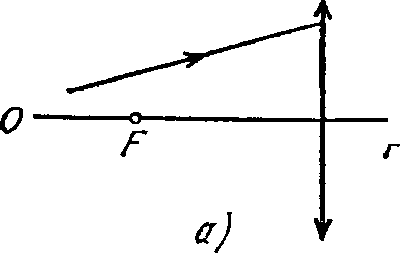
«7—O⁷ Ж О ®

Рис. 5.7.

F^r

F

Рис. 5.8.

а) 6)

24. Тонкая собирающая линза с фокусным расстоянием f = = 25 см проецирует изображение предмета на экран, отстоящий от линзы на расстоянии I = 5,0 м. Экран придвинули к линзе на Δ/ = 18 см. На сколько следует переместить предмет, чтобы опять получить четкое изображение его на эране?

25. Источник света находится на расстоянии / = 90 см от экрана. Тонкая собирающая линза, помещенная между источником света и экраном, дает четкое изображение источника при двух положениях. Определить фокусное расстояние линзы, если:

а) расстояние между обоими положениями линзы Δ/ = 30 см;

б) поперечные размеры изображения при одном положении линзы в η = 4,0 раза больше, чем при другом.

24. Между предметом и экраном, положения которых неиз­менны, помещают тонкую собирающую линзу. Перемещением линзы находят два положения, при которых на экране образуется четкое изображение предмета. Найти поперечный размер предмета, если при одном положении линзы размер изображения К = 2,0 мм, а при другом tf = 4,5 мм.

25. Тонкая собирающая линза с относительным отверстием £):/==1: З_у5 (D — диаметр линзы, f — ее фокусное расстояние) дает изображение достаточно удаленного предмета на фотопластинке. Яркость предмета L = 260 кд/м². Потери света в линзе составляют α = 0,10. Найти освещенность изображения.

26. 7*

    Как зависит от диаметра D тонкой собирающей линзы яркость действительного изображения, если его рассматривать:

195

а) непосредственно;

б) на белом экране, рассеивающем по закону Ламберта?

5.4Θ. Имеются две тонкие симметричные линзы: одна собираю­щая с показателем преломления п_г — 1,70, другая рассеивающая с п₂ = 1,51. Обе линзы имеют одинаковый радиус кривизны поверх­ностей R = 10 см. Линзы сложили вплотную и погрузили в воду. Каково фокусное расстояние этой системы в воде?

5.41. Определить фокусное расстояние вогнутого сферического зеркала, которое представляет собой тонкую симметричную двояко­выпуклую стеклянную линзу с посеребренной одной поверхностью.

Радиус кривизны поверхности линзы R = 40 см.

5.42. На рис. 5.9 показана ^y центрированная система, состоя­щая из трех тонких линз. Си-

+10,0 цп Рис. 5.9.

ЧО,Одп

+IO_jOjw

в воздухе.

стема находится Определить:

а) положение точки схожде­ния параллельного пучка, па­дающего слева, после прохож­дения через систему;

б) расстояние от первой линзы до точки, находящейся на оси слева от системы, при котором эта точка и ее изображение будут расположены симметрично относительно системы.

43. Галилеева труба 10-кратного увеличения при установке на бесконечность имеет длину 45 см. Определить:

а) фокусные расстояния объектива и окуляра трубы;

б) на какое расстояние надо передвинуть окуляр трубы, чтобы ясно видеть предметы на расстоянии 50 м.

43. Найти увеличение зрительной трубы кеплеровского типа, установленной на бесконечность, если D — диаметр оправы ее объектива, a d — диаметр изображения этой оправы, образуемого окуляром трубы.

44. При прохождении светового потока через зрительную трубу его интенсивность увеличивается в η = 4,0-10⁴ раз. Найти угловой размер удаленного предмета, если при наблюдении в эту трубу угловой размер его изображения ψ '= 2,0°.

45. Зрительную трубу кеплеровского типа с увеличением Г = 15 погрузили в воду, которая заполнила и ее внутреннюю часть. Чтобы система при тех же размерах стала опять телескопической, объектив заменили другим. Каково стало после этого увеличе­ние трубы в воде? Показатель преломления стекла окуляра η = 1,50.

    J	i 1 ■+-5,0 см	' 4
    1	г i	к ι	Г

46. О

    При каком увеличении Г зрительной трубы с диаметром объектива D = 6,0 см освещенность изображения объекта на сетчатке глаза будет не меньше, чем в отсутствие трубы? Диаметр зрачка глаза считать равным d₀ = 3,0 мм. Потерями света в трубе пренебречь.

47. Оптические силы объектива и окуляра микроскопа равны соответственно 100 и 20 дп. Увеличение микроскопа равно 50. Каково будет увеличение этого микроскопа, если расстояние между объективом и окуляром увеличить на 2,0 см?

48. Микроскоп имеет числовую апертуру sin α = 0,12, где α — угол полураствора конуса лучей, падающих на оправу объек­тива. Полагая диаметр зрачка глаза d₀ = 4,0 мм, определить увели­чение микроскопа, при котором:

а) диаметр светового пучка, выходящего из микроскопа, равен диаметру зрачка глаза;

б) освещенность изображения на сетчатке глаза не будет зави­сеть от увеличения (рассмотреть случай, когда световой пучок, проходящий через систему «микроскоп — глаз», ограничен опраЁой объектива).

43. Найти положение главных плоскостей, фокусов и узловых точек двояковыпуклой тонкой симметричной стеклянной линзы с радиусом кривизны поверхностей R = 7,50 см, если с одной стороны ее находится воздух, а с другой — вода.

44. Найти с помощью построения положение фокусов и глав­ных плоскостей центрированных оптических систем, показанных на рис. 5.10:

а) телеобъектив — система из собирающей и рассеивающей тонких линз (J₁ = 1,5 а, /₂ = — 1,5 а);

i	а	t
>	f t

O^r О-

f, Ъ

а)

j	S 4
У	г \	г

•О⁹

О

6)

Рис. 5.10.

б) система из двух собирающих тонких линз = 1,5 а, Z₂ = = 0,5 а);

в) толстая выпукло-вогнутая линза (d = 4 см, η = 1,5, O₁ = = + 50 дп, Ф₂ - — 50 дп).

5.52. Оптическая система находится в воздухе. Пусть OO' — ее оптическая ось, F и F^f — передний и задний фокусы, H и #'—

H

P

-O^r

■■O^t О

.P^r

б)

F

*) Рис. 5.11.

передняя и задняя главные плоскости, P и P^r—сопряженные точки. Найти построением:

а) положение F' и H^t (рис. 5.11, а);

б) положение точки S', сопряженной с точкой S (рис. 5.11, б);

в) положение F_y F^t и H^f (рис. 5.11, в, где показан ход луча до и после прохождения системы).

53. Пусть FhF' — передний и задний фокусы оптической системы, Я и Я' — ее передняя и задняя главные точки. Найти построением положение изображения S^f точки S для следующих относительных расположений точек S, F, F', Я и Я':

a) FSHH^fF^f; б) HSF^fFH^t; в) H^fSFFH; г) F^fH^fSHF.

53. Телеобъектив состоит из двух тонких линз — передней собирающей и задней рассеивающей с оптическими силами Ф_х = = + 10 дп и Ф₂ = — 10 дп. Найти:

а) фокусное расстояние и положение главных плоскостей этой системы, если расстояние между линзами d = 4,0 см;

б) расстояние d между линзами, при котором отношение фокус­ного расстояния / системы к расстоянию I между собирающей линзой и задним главным фокусом будет максимальным. Чему равно это отношение?

53. Рассчитать положение главных плоскостей и фокусов толстой выпукло-вогнутой стеклянной линзы, если радиус кривизны выпуклой поверхности R₁ = 10,0 см, вогнутой R₂ = 5,0 см и тол­щина линзы d = 3,0 см.

54. Центрированная оптическая система состоит из двух тонких линз с фокусными расстояниями Z₁ и /₂, причем расстояние между линзами равно d. Данную систему требуется заменить одной тонкой линзой, которая при любом положении объекта давала бы такое же поперечное увеличение, как и предыдущая система. Каким должно быть фокусное расстояние этой линзы и ее положение отно-

- сительно системы из двух линз?

53. Система состоит из собирающей тонкой симметричной стеклянной линзы с радиусом кривизны поверхностей R — 38 см и плоского зеркала, расположенного перпендикулярно к оптической оси линзы. Расстояние между линзой и зеркалом Z= 12 см. Какова будет оптическая сила этой системы, если пространство между линзой и зеркалом заполнить водой?

54. При какой толщине выпукло-вогнутая толстая стеклян­ная линза в воздухе будет:

а) телескопической, если радиус кривизны ее выпуклой поверх­ности больше, чем радиус кривизны вогнутой поверхности, на AR = 1,5 см?

б) иметь оптическую силу, равную —1,0 дп, если радиусы кривизны ее выпуклой и вогнутой поверхностей равны соответ­ственно 10,0 и 7,5 см?

53. Найти положение главных плоскостей, фокусное расстоя­ние и знак оптической силы выпукло-вогнутой толстой стеклянной линзы, у которой:

а) толщина равна d, а радиусы кривизны поверхностей одина­ковы и равны jR;

б) преломляющие поверхности концентрические с радиусами кривизны R₁ и R₂ (R₂ > Ri)-

53. Телескопическая система образована из двух стеклянных шаров, радиусы которых Ri = 5,0 см и R₂ = 1,0 см. Каковы рас­стояние между центрами этих шаров и увеличение системы, если объективом является больший шар?

54. Две одинаковые симметричные двояковыпуклые толстые линзы сложены вплотную. Толщина каждой линзы равна радиусу кривизны ее поверхностей, d = R = 3,0 см. Найти оптическую силу этой системы в воздухе.

55. При распространении света в изотропной среде с медленно изменяющимся от точки к точке показателем преломления η радиус кривизны ρ луча определяется формулой

7 = Ш (In ή),

где производная берется по направлению главной нормали к лучу. Получить эту формулу, имея в виду, что в такой среде справедлив закон преломления η sin# = const, где θ — угол между лучом и направлением grad η в данной точке.

53. Найти радиус кривизны светового луча, распространяю­щегося в горизонтальном направлении вблизи поверхности Земли, где градиент показателя преломления воздуха равен около 3· 10"* м^-1. При каком значении этого градиента луч света распространялся бы по окружности вокруг Земли?

5.2. Интерференция света

φ Ширина интерференционной полосы:

Ax=-^-X_t (5.2а)

d

где I — расстояние от экрана до источников, d—расстояние между источниками.

φ Временная и пространственная когерентности. Соответственно длина и раднуе когерентности:

^ког д^ i ΡκοΓ^ψ"» (5.26)

где ψ— угловой размер источника.

φ Условие максимумов при интерференции света, отраженного от тонкой пластинки толщины b:

2 Ъ Vn*-sin* = (k +V₂) λ, (5.2в)

где k~ целое число.

9 Кольца Ньютона при отражении света от поверхностей воздушной прослойки, которая образована между стеклянной пластинкой и соприкасаю­щейся с ней выпуклой поверхностью линзы радиуса R. Радиусы колец:

(5.2г)

причем кольца светлые, если £ = 1, 3, 5, ... , и темные, если k =2, 4, 6, ... Значению & = 0 соответствует середина центрального темного пятна.

53. Показать, что при сложении двух гармонических колеба­ний средняя по времени энергия результирующего колебания равна сумме энергий каждого из них, если оба колебания:

а) имеют одинаковое направление и некогерентны, причем все значения их разности фаз равновероятны;

б) взаимно перпендикулярны, имеют одну и ту же частоту и произвольную разность фаз.

53. Найти графически амплитуду колебания, которое возни­кает в результате сложения следующих трех колебаний одного направления:

I₁ =Z a cos со/, ξ₂ = 2a sin со/, ξ₃ = 1,5α cos (со/ ;-f- π/3).

53. Некоторое колебание возникает в результате сложения когерентных колебаний одного направления, имеющих следующий

вид: Ik^z= CL cos[co/ + (k — 1)φ], где k — номер ко­лебания (k = 1, 2, ..., Ν), φ — разность фаз между k-ы и (k — 1)-м колебаниями. Найти амплитуду ре­зультирующего колебания.

5.67. Система (рис. 5.12) состоит из двух точеч­ных когерентных излучателей 1 и 2, которые рас­положены в некоторой плоскости так, что их ди- польные моменты перпендикулярны к этой плос- Рис. 5Л2. кости. Расстояние между излучателями d, длина волны излучения λ. Имея в виду, что колебания излучателя 2 отстают по фазе на φ (φ < π) от колебаний из­лучателя найти:

а) углы θ, в которых интенсивность излучения максимальна;

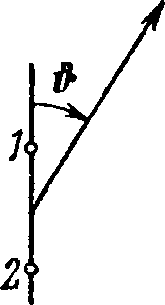
б) условия, при которых в направлении θ = π интенсивность излучения будет максимальна, а в противоположном направлении — минимальна.

5.68. Неподвижная излучающая система состоит из линейной цепочки параллельных вибраторов, отстоящих друг от друга на расстояние d, причем фаза колебаний вибраторов линейно меняется вдоль цепочки. Найти зависимость от времени разности фаз Δφ между соседними вибраторами, при которой главный максимум излучения системы будет совершать круговой «обзор» местности с постоянной угловой скоростью ω.

Рис. 5.13,

5.69. В опыте Ллойда (рис. 5.13) световая волна, исходящая непосредственно из источника S (узкой щели), интерферирует с вол­ной, отраженной от зеркала 3. В результате на экране Э образуется

система интерференционных полос. Расстояние от источника до экрана I = 100 см. При некотором положении источника ширина интерференционной полосы на экране Ax = 0,25 мм, а после того как источник отодвинули от плоскости зеркала на Ah = 0,60 мм, ширина полос уменьшилась в η = 1,5 раза. Найти длину волны света.

70. Две когерентные плоские световые волны, угол между направлениями распространения которых ψ <; 1, падают почти нормально на экран. Амплитуды волн одинаковы. Показать, что расстояние между соседними максимумами на экране Ax = λ/ψ, где λ — длина волны.

71. На рис. 5.14 показана интерференционная схема с бизер- калами Френеля. Угол между зеркалами а = 12', расстояния от

линии пересечения зеркал до узкой щели S и экрана Э равны соот­ветственно г = 10,0 см и b = 130 см. Длина волны света λ = = 0,55 мкм. Определить:

а) ширину интерференционной полосы на экране и число возмож­ных максимумов;

б) сдвиг интерференционной картины на экране при смещении щели на Ы = 1,0 мм по дуге радиуса г с центром в точке О;

в) при какой максимальной ширине щели б_макс интерференцион­ные полосы на экране будут наблюдаться еще достаточно отчет­ливо?

70. Плоская световая волна падает на бизеркала Френеля, угол между которыми α = 2,0'. Определить длину волны света, если ширина интерференционной полосы на экране Ax == 0,55 мм.

71. Линзу диаметром 5,0 см и с фокусным расстоянием / = = 25,0 см разрезали по диаметру на две одинаковые половины, причем удаленным оказался слой толщины а= 1,00 мм. После этого обе половины сдвинули до соприкосновения и в фокальной плоскости полученной таким образом билинзы поместили узкую щель, испускающую монохроматический свет с длиной волны λ = 0,60 мкм. За билинзой расположили экран на расстоянии b = 50 см от нее. Определить:

а) ширину интерференционной полосы на экране и число возмож­ных максимумов;

б) максимальную ширину щели б_макс, при которой интерферен­ционные полосы на экране будут наблюдаться еще достаточно отчет­ливо..

Расстояния от бипризмы Френеля до узкой щели и экрана равны соответственно а = 25 см и b = 100 см. Бипризма стеклян­ная с преломляющим углом θ =20'. Найти длину волны света,

если ширина интерференционной полосы на экране Ax = 0,55 мм.

5.75. Плоская световая волна с λ = = 0,70 мкм падает нормально на осно­вание бипризмы, сделанной из стекла (п = 1,520) с преломляющим углом θ = 5,0°. За бипризмой (рис. 5.15) находится плоскопараллельная стек­лянная пластинка, и пространство ме­жду ними заполнено бензолом (n^f = = 1,500). Найти ширину интерференционной полосы на экране Э, расположенном за этой системой.

\/5.76. Плоская монохроматическая световая волна падает нор­мально на диафрагму с двумя узкими щелями, отстоящими друг от друга на расстояние d = 2,5 мм. На экране, расположенном за диафрагмой на I = 100 см, образуется система интерференционных полос. На какое расстояние и в какую сторону сместятся эти полосы, если одну из щелей перекрыть стеклянной пластинкой толщины h = 10 мкм?

V 5.77. На рис. 5.16 показана схема интерферометра, служащего для измерения показателей преломления прозрачных веществ.

Рис. 5.16.

А

Здесь S — узкая щель, освещаемая монохроматическим светом χ = 589 нм, 1 я 2 — две одинаковые трубки с воздухом, длина каждой из которых I = 10,0 см, Д —диафрагма с двумя щелями. Когда воздух в трубке 1 заменили аммиаком, то интерференционная картина на экране Э сместилась вверх на N= 17 полос. Показатель преломления воздуха η = 1,000277. Определить показатель пре­ломления аммиака.

!

Рис. 5.15.

5.78. Электромагнитная волна падает нормально на драницу раздела двух изотропных диэлектриков с показателями преломле­ния Ii₁ и п₂. Воспользовавшись условием непрерывности танген­циальной составляющей вектора E на границе раздела и законом сохранения энергии, показать, что на границе раздела вектор Е: а) проходящей волны не испытывает скачка фазы;

б) отраженной волны испытывает скачок фазы на π, если отра­жение происходит от оптически более плотной среды.

79. На тонкую пленку (п = 1,33) падает параллельный пучок белого света. Угол падения A₁ = 52°. При какой толщине пленки зеркально отраженный свет будет наиболее сильно окрашен в жел- тьш цвет (λ = 0,60 мкм)?

80. Найти минимальную толщину пленки с показателем пре­ломления 1,33, при которой свет с длиной волны 0,64 мкм испыты­вает максимальное отражение, а свет с длиной волны 0,40 мкм не отражается совсем. Угол падения света равен 30°.

81. Для уменьшения потерь света из-за отражения от поверх­ности стекла последнее покрывают тонким слоем вещества с показа­телем преломления n^r = ]/Vz, где η — показатель преломления стекла. В этом случае амплитуды световых колебаний, отраженных от обеих поверхностей такого слоя, будут одинаковыми. При какой толщине этого слоя отражательная способность стекла в направлении нормали будет равна нулю для света с длиной волны λ.

V 5.82. Рассеянный монохроматический свет с λ = 0,60 мкм падает на Тонкую пленку вещества с показателем преломления η = 1,5. Определить толщину пленки, если угловое расстояние между соседними максимумами, наблюдае­мыми в отраженном свете под углами 3 с нормалью, близкими к Φ = 45°, _д равно 6ft = 3,0°.

83. Монохроматический свет про- I—^^ ходит через отверстие в экране Э " (рис. 5.17) и, отразившись от тонкой плоско-параллельной стеклянной пла­стинки Я, образует на экране систе- Рис- SA7. му интерференционных полос равного наклона. Толщина пластинки d, расстояние между ней и экра­ном I_i радиусы i-ro и k-το темных колец T_i и r_k. Учитывая, что Ujk ^ h найти длину волны света.

84. Плоская монохроматическая световая волна длины λ падает на поверхность стеклянного клина, угол между гранями которого α <; 1. Плоскость падения перпендикулярна к ребру клина, угол падения O⁴₁. Найти расстояние между соседними максимумами интер­ференционных полос на экране, расположенном перпендикулярно к отраженному свету,

^85^'Свет с длиной волны λ = 0,55 мкм от удаленного точечного источника падает нормально на поверхность стеклянного клина. В отраженном /свете наблюдают систему интерференционных полос, расстояьЦе между соседними максимумами которых на поверхности клина Ax' = 0,21 мм. Найти:

а) угол между гранями клина;

б) степень монохроматичности света (Δλ/λ), если исчезновение интерференционных полос наблюдается на расстоянии I ж 1,5 см от вершины клина.

·* 5.86. Плоско-выпуклая стеклянная линза выпуклой поверх­ностью соприкасается со стеклянной пластинкой. Радиус кривизны выпуклой поверхности линзы R_y длина волны света λ. Найтширину Δ г кольца Ньютона в зависимости от его радиуса г в области, где Ar < г.

87. Плоско-выпуклая стеклянная линза с радиусом кривизны R = 40 см соприкасается выпуклой поверхностью со стеклянной пластинкой. При этом в отраженном свете радиус некоторого кольца г =7 2,5 мм. Наблюдая за данным кольцом, линзу осторожно ото­двинули от пластинки на Δ/г = 5,0 мкм. Каким стал радиус этого кольца?

88. На вершине сферической поверхности плоско-выпуклой стеклянной линзы имеется сошлифованный плоский участок радиуса r₀ = 3,0 мм, которым она соприкасается со стеклянной пластинкой. Радиус кривизны выпуклой поверхности линзы R = 150 см. Найти радиус шестого светлого кольца при наблюдении в отраженном свете с длиной волны λ = 655 нм.

89. Плоско-выпуклая стеклянная линза с радиусом кривизны сферической поверхности R= 12,5 см прижата к стеклянной пластинке. Диаметры десятого и пятнадцатого темных колец Нью­тона в отраженном свете равны Ci₁ = 1,00 мм и d₂ = 1,50 мм. Опре­делить длину волны света.

Ni 5.90. Две плоско-выпуклые тонкие стеклянные линзы сопри­касаются своими сферическими поверхностями. Найти оптическую силу такой системы, если в отраженном свете с λ = 0,60 мкм диаметр пятого светлого кольца d = 1,50 мм.

5.91. Две соприкасающиеся тонкие симметричные стеклянные линзы — одна двояковыпуклая, другая двояковогнутая — обра­зуют систему с оптической силой Φ = 0,50 дп. В свете с λ = 0,61 мкм, отраженном от этой системы, наблюдают кольца Ньютона. Опреде­лить:

а) радиус десятого темного кольца;

б) как изменится радиус этого кольца, если пространство между линзами заполнить водой?

* 5.92. Сферическая поверхность плоско-выпуклой линзы сопри­касается со стеклянной пластинкой. Пространство между линзой и пластинкой заполнено сероуглеродом. Показатели преломления линзы, сероуглерода и пластинки равны соответственно H₁ — 1,50, п₂ = 1,63 и n_s = 1,70. Радиус кривизны сферической поверхности линзы R = 100 см. Определить радиус пятого темного кольца Нью­тона в отраженном свете с λ = 0,50 мкм.

93. В двухлучевом интерферометре используется оранжевая линия ртути, состоящая из двух компонент с длинами волн X₁ = = 576,97 им и X₂ = 579,03 нм. При каком наименьшем порядке интерференции четкость интерференционной картины будет наи­худшей?

94. В интерферометре Майкельсона использовалась желтая линия натрия, состоящая из двух компонент с длинами волн X₁ =

= 589,0 нм и I₂ = 589,6 нм. При поступательном перемещении одного из зеркал интерференционная картина периодически исче­зала (почему?). Найти перемещение зеркала между двумя последо­вательными появлениями наиболее четкой интерференционной кар­тины.

5.95. При освещении эталона Фабри — Перо расходящимся монохроматическим светом с длиной волны λ в фокальной плоскости линзы возникает интерференционная картина — система концен­трических колец (рис. 5.18). Толщина эталона равна.d. Определить, как зависит от порядка интерференции:

а) расположение колец;

б) угловая ширина полос интерференции.

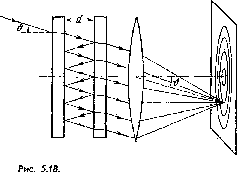
5.96. Найти для эталона Фабри — Перо, толщина которого d — 2,5 см:

а) максимальный порядок интерференции света с длиной волны λ = 0,50 мкм;

б) дисперсионную область Δλ, т. е. спектральный интер$рл длин волн, для которого еще нет перекрытия с другими порядками интерференции, если наблюдение ведется вблизи λ = 0,50 мкм.

5.3. Дифракция света

0 Радиус внешней границы k-й зоны Френеля:

г*^k = \, 2, 3. ... (5.3а)

0 Спираль Корню (рис. 5.19). Числа на этой спирали —значения пара­метра у. Для плоской волны ν — χ V2IbX_t где χ и Ь — расстояния, характери­зующие положение элемента dS волновой поверхности относительно точки наблюдения P₁ как показано в левом верхнем углу рисунка.

0 Дифракция Фраунгофера от щели, свет падает нормально. Условие минимумов интенсивности:

&sinft = ztM, £ = 1,2,3,..., (035)

где & — ширина щели, ft— угол дифракции.

UKHI

ы—

* /dS

Рис. 5Л9.

φ Дифракционная решетка, свет падает нормально. Условие главных фра- унгоферовых максимумов:

(5.3в) (5.3г)

(5.3д)

d sin ft = Ji kX, £ = 0, 1,2,...«

условие добавочных минимумов:

k'

d sin ft = ± Trh N

Где £'=1, 2, ... , кроме 0, N_i 2N_t ...

φ Угловая дисперсия дифракционной решетки:

δλ d cos ft *

(5.3е)

φ Разрешающая способность дифракционной решетки:

где N — число штрихов решетки. 206

0 Разрешающая сила объектива

где δψ—наименьшее угловое расстояние, разрешаемое объективом, D —диаметр последнего.

0 Формула Брэгга —Вульфа. Условие дифракционных максимумов:

2d sin α = J: kX, (5.3з)

где d — межплоскостное расстояние, а —угол скольжения, k=l, 2, 3,

97. Плоская световая волна падает нормально на диафрагму с круглым отверстием, которое открывает первые N зон Френеля — для точки P на экране, отстоящем от диафрагмы на расстояние Ь. Длина волны света равна λ. Найти интенсивность света I₀ перед диафрагмой, если известно распределение интенсивности света на экране / (г), где г — расстояние до точки P.

98. Точечный источник света с длиной волны λ = 0,50 мкм расположен на расстоянии а = 100 см перед диафрагмой с круг­лым отверстием радиуса г = 1,0 мм. Найти расстояние b от диа­фрагмы до точки наблюдения, для которой число зон Френеля в от­верстии составляет k = 3.

ν 5.99. Между точечным источником света и экраном поместили диафрагму с круглым отверстием, радиус которого г можно менять в процессе опыта. Расстояния от диафрагмы до источника и экрана равны а = 100 см и b = 125 см. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при r_x = 1,00 мм и следующий максимум при r₂ = 1,29 мм.

100. Плоская монохроматическая световая волна с интенсив­ностью I₀ падает нормально на непрозрачный экран с круглым отверстием. Какова интенсивность света / за экраном в точке, для которой отверстие:

а) равно первой зоне Френеля; внутренней половине первой зоны;

б) сделали равным первой зоне Френеля и затем закрыли его половину (по диаметру)?

100. Монохроматическая плоская световая волна с интенсив­ностью I₀ падает нормально на непрозрачный диск, закрывающий для точки наблюдения P первую зону Френеля. Какова стала ин­тенсивность света / в точке P после того, как у диска удалили:

а) половину (по диаметру);

б) половину внешней половины первой зоны Френеля (по диа­метру)?

100. Плоская монохроматическая световая волна с интенсив­ностью I₀ падает нормально на поверхности непрозрачных экранов, показанных на рис. 5.20. Найти интенсивность света / в точке Р:

а) расположенной за вершиной угла экранов 1—3 и за краем полуплоскости 4\

б) для которой закругленный край экранов 5—5 совпадает с границей первой зоны Френеля.

Обобщить полученные результаты для экранов 1—4 одной фор­мулой; то же — для экранов 5—5.

V/,

Ш

β

P

5

Рис. 5.20.

5.103. Плоская световая волна с λ = 0,60 мкм падает нормально на достаточно большую стеклянную пластинку, на противоположной стороне которой сделана круглая выемка (рис. 5.21), Для точки

наблюдения P она представляет собой первые полторы зоны Френеля. Найти глубину h выемки, при которой интенсивность света в точке P будет:

а) максимальной;

б) минимальной;

в) равной интенсивности падающего света. 5.104. Плоская световая волна длины λ и

интенсивности I₀ падает нормально на боль­шую стеклянную пластинку, противополож­ная сторона которой представляет собой не­прозрачный экран с круглым отверстием, рав­ным первой зоне Френеля для точки наблюдения Р. В середине отверстия сделана круглая выемка, равная половине зоны Фре­неля. При какой глубине h этой выемки интенсивность света в точке P будет максимальной? Чему она равна?

^J 5.105. Плоская световая волна с λ = 0,57 мкм падает нормально на поверхность стеклянного (п = 1,60) диска, который закрывает полторы зоны Френеля для точки наблюдения P. При какой мини­мальной толщине этого диска интенсивность света в точке P будет максимальной? Учесть интерференцию света при прохождении диска.

I I л I I

Рис. 5.21.

5.106. На пути плоской световой волны с λ = 0,54 мкм поста­вили тонкую собирающую линзу с фокусным расстоянием f = = 50 см, непосредственно за ней — диафрагму с круглым отвер­стием и на расстоянии b = 75 см от диафрагмы — экран. При ка­

ких радиусах отверстия центр дифракционной картины на экране имеет максимальную освещенность?

107. Плоская монохроматическая световая волна падает нор­мально на круглое отверстие. На расстоянии b = 9,0 м от него на­ходится экран, где наблюдают некоторую дифракционную картину. Диаметр отверстия уменьшили в η = 3,0 раза. Найти новое рассто­яние Ь\ на котором надо поместить экран, чтобы получить на нем дифракционную картину, подобную той, что в предыдущем случае, но уменьшенную в η раз.

108. Между источником света с λ = 0,55 мкм и фотопластин­кой поместили непрозрачный шарик диаметра D = 40 мм. Расстоя­ние между источником и шариком а = 12 м, а между шариком и фо­топластинкой b = 18 м. Найти:

а) размер изображения у' на пластинке, если поперечный раз­мер источника у 6,0 мм;

б) минимальную высоту неровностей, хаотически покрывающих поверхность шарика, при которой последний уже будет загоражи­вать свет.

Примечание. Расчет и опыт показывают, что это происхо­дит тогда, когда высота неровностей сравнима с шириной зоны Фре­неля, по которой проходит край непрозрачного экрана.

107. Точечный источник монохроматического света расположен перед зонной пластинкой на расстоянии а — 1,5 м от нее. Изображе­ние источника образуется на расстоянии & = 1,0 м от пластинки. Найти фокусное расстояние зонной пластинки.

I 5.110. Плоская световая волна с λ= | .J ^

— 0,60 мкм и интенсивностью Z₀ падает нор­мально на большую стеклянную пластинку, профиль которой показан на рис. 5.22. При какой высоте h уступа интенсивность света в точках, расположенных под ним, будет:

а) минимальна;

б) вдвое меньше /₀ (потерями на отраже- Рис. 5.22. ния пренебречь).

111. Плоская монохроматическая световая волна па^ет нор­мально на непрозрачную полуплоскость. На расстоянии b f= 100 см за ней находится экран. Найти с помощью спирали Корню (ркс. 5.19}:

а) отношение интенсивностей первого максимума и ссседкего 'с ним минимума;

б) длину волны света, если расстояние между двумя первыми максимумами Ax = 0,63 мм.

111. Плоская световая волна длины 0,60 мкм падает нормально на непрозрачную длинную полоску ширины 0,70 мм. За ней на расстоянии 100 см находится экран. Найти с помощью рис. 5.19 отношение интенсивностей света в середине дифракционной картины и на краях геометрической тени.

112. Плоская монохроматическая световая волна падает нор­мально на длинную прямоугольную щель, за которой на^расЪтоя-

113. нии b = 60 см находится экран. Сначала ширину щели установили такой, что в середине дифракционной картины на экране наблю­дался наиболее глубокий минимум. Раздвинув после этого щель на Ah = 0,70 мм, получили в центре картины следующий минимум. Найти длину волны света.

114. Плоская световая волна с λ = 0,65 мкм падает нормально на большую стеклянную пластинку, на противоположной стороне которой сделана длинная прямоугольная выемка ширины 0,60 мм. Найти с помощью рис. 5.19 глубину выемки h, при которой в сере­дине дифракционной картины на экране, отстоящем на 77 см от пла­стинки, будет максимум освещенности.

115. Плоская световая волна с λ = 0,65 мкм падает нормально на большую стеклянную пластинку, на противоположной стороне

которой имеется уступ и непрозрачная по­лоска ширины а = 0,30 мм (рис. 5.23). На расстоянии b— 110 см от пластинки нахо­дится экран. Высота уступа h подобрана такой, что в точке 2 на экране интенсивность света оказывается максимально возможной. Найти с помощью рис. 5.19 отношение интенсив- ностей в точках 1 и 2.

5.116. Плоская монохроматическая свето-

УШ/У/////////}У//ш//, ^{вая волна} интенсивности /₀ падает нор­мально на непрозрачный экран, в котором Рис. 5-23. прорезана длинная щель с полукруглым вы­

Рис. 5.25.

резом на одной из сторон (рис. 5.24). Край выреза совпадает с границей первой зоны Френеля для точки наблюдения Р. Ширина щели составляет 0,90 радиуса выреза. Найти с помощью рис. 5.19 интенсивность света в точке Р.

ТШТШШШШШ/.

Рис. 5.24.

117. Плоская монохроматическая световая волна падает нор­мально на непрозрачный экран с длинной щелью, форма которой показана на рис. 5.25. Найти с помощью рис. 5.19 отношение интен- сирностей света в точках 2 и 5, расположенных за экраном на од­ном и том же расстоянии от него, если для точки 3 закругленный край щели совпадает с границей первой зоны Френеля.

118. F

     JL·

     φ

     φ φ Ψ .ι. г. ф

     V мЬ

     M hi M

     a

     Плоская монохроматическая световая волна падает нор­мально на непрозрачный экран, имеющий вид длинной полоски с круглым отверстием посередине. Для точки наблюдения P отвер­стие представляет собой половину зоны Френеля, причем его диа­метр в η = 1,07 раза меньше ширины полоски. Найти с помощью

119. рис. 5.19 интенсивность света в точке P_i если интенсивность падаю­щего света равна /₀.

V 5.119. Свет с длиной волны λ падает нормально на длинную прямоугольную щель ширины Ь. Найти угловое распределение ин­тенсивности света при фраунгоферовой дифракции, а также угловое положение минимумов.

120. Воспользовавшись результатом, полученным в предыду­щей задаче, найти условия, определяющие угловое положение мак­симумов первого, второго и третьего порядков.

121. Свет с длиной волны λ = 0,50 мкм падает на щель ширины b = 10 мкм под углом Ф₀ = 30° к ее нормали. Найти угловое поло­жение первых минимумов, расположенных по обе стороны централь­ного фраунгоферова максимума.

122. Плоская световая волна с λ = 0,60 мкм падает нормально на грань стеклянного клина с преломляющим углом θ = 15°. На противоположной, непрозрачной, грани имеется щель ширины b = 10 мкм, параллельная ребру клина. Найти:

а) угол ΔΦ между направлением на фраунгоферов максимум нулевого порядка и направлением падающего света;

б) угловую ширину фраунгоферова максимума нулевого порядка.

5Д23. Монохроматический свет падает на отражательную диф­ракционную решетку с периодом d = 1,0 мм под углом скольжения а₀ = 1,0°_г Под углом скольжения а = 3,0° образуется фраунгофе­ров максимум второго порядка. Найти длину волны света.

5.124. Изобразить примерную дифракционную картину, возни­кающую при дифракции Фраунгофера от решетки из трех одинако­вых щелей, если отношение периода решетки к ширине щели равно:

а) двум; б) трем, г 5.125. При нормальном падении света на дифракционную ре­шетку угол дифракции для линии X₁ = 0,65 мкм во втором порядке равен 45°. Найти угол дифракции для линии λ^ = 0,50 мкм в третьем порядке.

¢/5.126. Свет с длиной волны 535 нм падает нормально на дифрак­ционную решетку. Найти ее период, если одному из фраунгоферо- вых максимумов соответствует угол дифракции 35° и наибольший порядок спектра равен пяти.

127. Определить длину волны монохроматического света, падающего нормально на дифракционную решетку с периодом d = 2,2 мкм, если угол между направлениями на фраунгоферовы максимумы первого и второго порядков Δ ft — 15°.

128. Свет с длиной волны 530 нм падает на прозрачную дифрак­ционную решетку, период которой равен 1,50 мкм. Найти угол с нормалью к решетке, под которым образуется фраунгоферов мак­симум наибольшего порядка, если свет падает на решетку:

а) нормально; б) под углом 60° к нормали.

127. Свет с длиной волны λ == 0,60 мкм падает нормально на дифракционную решетку, которая нанесена на плоской поверхно­сти плсско-выпуклой цилиндрической стеклянной линзы с радиу­сом кривизны R = 20 см. Период решетки d = 6,0 мкм. Найти рас­стояние между симметрично расположенными главными максиму­мами первого порядка в фокальной плоскости этой линзы.

128. Плоская световая волна с λ = 0,50 мкм падает нормально на грань стеклянного клина с углом θ — 30°. На противоположной грани клина нанесена прозрачная дифракционная решетка с перио­дом d = 2,00 мкм, штрихи которой параллельны ребру клина. Найти углы между направлением падающего света и направлениями на главные фраунгоферовы максимумы нулевого и первого поряд­ков. Каков максимальный порядок спектра? Под каким углом к на­правлению падающего света он будет наблюдаться?

129. Плоская световая волна длины λ падает нормально на фазовую дифракционную решетку, профиль которой показан на рис. 5.26. Решетка нанесена на стеклянной пластинке с показателем преломления η. Найти глубину h штрихов, при которой интенсив­ность центрального фраунгоферова максимума равна нулю. Каков при этом угол дифракции, соответствующий первому максимуму?

К О

Рис. 5.26. Рис. 5.27.

127. На рис. 5.27 показана схема установки для наблюдения дифракции света на ультразвуке. Плоская световая волна с λ = = 0,55 мкм проходит через кювету К с водой, в которой возбуждена стоячая ультразвуковая волна с частотой ν = 4,7 МГц. В резуль­тате дифракции света на оптически неоднородной периодической структуре в фокальной плоскости объектива О с фокусным расстоя­нием / = 35 см возникает дифракционный спектр. Расстояние между соседними максимумами Ax — 0,60 мм. Найти скорость распростра­нения ультразвуковых колебаний в воде.

128. Для измерения методом Майкельсона углового расстоя­ния ψ между компонентами двойной звезды перед объективом теле­скопа поместили диафрагму с двумя узкими параллельными щелями, расстояние d между которыми можно менять. Уменьшая d, обнару­жили первое ухудшение видимости дифракционной картины в фо­кальной плоскости объектива при d = 95 см. Найти ψ, считая длину волны света λ = 0,55 мкм.

129. Прозрачная дифракционная решетка имеет период d = = 1,50 мкм. Найти угловую дисперсию D (в угл. мин/нм), соответ­ствующую максимуму наибольшего порядка спектральной линии с λ — 530 нм, если свет падает на решетку

а) нормально; б) под углом #₀ = 45° к нормали.

127. Свет с длиной волны λ падает нормально на дифракцион­ную решетку. Найти ее угловую дисперсию в зависимости от угла дифракции

128. Свет с λ — 589,0 нм падает нормально на дифракционную решетку с периодом d — 2,5 мкм, содержащую N = 10 ООО штри­хов. Найти угловую ширину дифракционного максимума второго порядка.

129. Показать, что при нормальном падении света на дифрак­ционную решетку максимальная величина ее разрешающей способ­ности не может превышать значения //λ, где I — ширина решетки, λ — длина волны света.

130. Показать на примере дифракционной решетки, что раз­ность частот двух максимумов, разрешаемых по критерию Рэлея, равна обратной величине разности времен прохождения самых крайних интерферирующих колебаний, т. е, δν = 1 /Ы.

131. Свет, содержащий две спектральные линии с длинами волн 600,000 и 600,050 нм, падает нормально на дифракционную решетку ширины 10,0 мм. Под некоторым углом дифракции # эти ли­нии оказались на пределе разрешения (по критерию Рэлея). Найти

132. Свет падает нормально на прозрачную дифракционную решетку ширины / = 6,5 см, имеющую 200 штрихов на миллиметр. Исследуемый спектр содержит спектральную линию с λ — 670,8 нм, которая состоит из двух компонент, отличающихся на δλ — 0,015 нм. Найти:

а) в каком порядке спектра эти компоненты будут разрешены;

б) наименьшую разность длин волн, которую может разрешить эта решетка в области λ 670 нм.

127. При нормальном падении света на прозрачную дифрак­ционную решетку ширины 10 мм обнаружено, что компоненты жел­той линии натрия (589,0 и 589,6 нм) оказываются разрешенными, начиная с пятого порядка спектра. Оценить:

а) период этой решетки;

б) при какой ширине решетки с таким же периодом можно раз­решить в третьем порядке дублет спектральной линии с λ = 460,0 нм, компоненты которого отличаются на 0,13 нм.

127. Прозрачная дифракционная решетка кварцевого спектро­графа имеет ширину 25 мм и содержит 250 штрихов на миллиметр. Фокусное расстояние объектива, в фокальной плоскости которого находится фотопластинка, равно 80 см. Свет падает на решетку нормально. Исследуемый спектр содержит спектральную линию, компоненты дублета которой имеют длины волн 310,154 и 310,184 нм. Определить:

а) расстояния на фотопластинке между компонентами этого дуб­лета в спектрах первого и второго порядков;

б) будут ли они разрешены в этих порядках спектра.

127. Для трехгранной призмы спектрографа предельная разре­шающая способность λ/δλ обусловлена дифракцией света от краев призмы (как от щели). При установке призмы на угол наименьшего

отклонения в соответствии с критерием Рэлея

λ/δλ = £? I dn/άλ I,

где b — ширина основания призмы (рис. 5.28), dti/άλ — дисперсия ее вещества. Вывести эту формулу.

С

Рис. 5.28.

127. Трехгранная призма спектрографа изгстоЕлена из стекла, показатель преломления которого зависит от длины волны сЕета как η = А + β/λ², где AwB — постоянные, причем В = 0,010 мкм². Воспользовавшись формулой из предыдущей задачи, найти:

а) зависимость разрешающей способности призмы от λ; вычис­лить λ/δλ вблизи λ_χ = 434 нм и λ₂ = 656 нм, если ширина основания призмы Ь = 5,0 см;

б) ширину основания призмы, способной разрешить желтый дублет натрия (589,0 и 589,6 нм).

127. Какой должна быть ширина основания трехгранной призмы, чтобы она имела такую же разрешающую способность, как и дифракционная решетка из 10 000 штрихов во втором порядке спектра?

128. Имеется зрительная труба с диаметром объектива D = — 5,0 см. Определить разрешающую способность объектива трубы и минимальное расстояние между двумя точками, находящимися на расстоянии I — 3,0 км от трубы, которое она может разрешить (считать λ = 0,55 мкм).

129. Вычислить наименьшее расстояние между двумя точками на Луне, которое можно разрешить рефлектором с диаметром зер­кала в 5 м. Считать, что длина волны света λ = 0,55 мкм.

130. Определить минимальное увеличение зрительной трубы с диаметром объектива D = 5,0 см, при котором разрешающая спо­собность ее объектива будет полностью использована, если диаметр зрачка глаза d₀ = 4,0 мм.

131. Имеется микроскоп с числовой апертурой объектива sin α = 0,24, где а — угол полураствора конуса лучей, падающих на оправу объектива. Найти минимальное разрешаемое расстояние для этого микроскопа при оптимальном освещении объекта светом с длиной волны λ — 0,55 мкм.

132. Найти минимальное увеличение микроскопа с числовой апертурой объектива sin α = 0,24, при котором разрешающая спо­собность его объектива будет полностью использована, если диа­метр зрачка глаза d₀ = 4,0 мм.

133. Пучок рентгеновских лучей с длиной волны λ падает под углом скольжения 60,0° на линейную цепочку из рассеивающих центров с периодом а. Найти углы скольжения, соответствующие всем дифракционным максимумам, если λ = ²Да.

134. Пучок рентгеновских лучей с длиной волны λ = 40 пм падает нормально на плоскую прямоугольную решетку из рассеи­вающих центров и дает на плоском экране, расположенном на рас­стоянии / = 10 см от решетки, систему у. дифракционных максимумов (рис. 5.29). Найти периоды решетки а и Ь * · . соответственно вдоль осей χ и у, если ' * расстояния между симметрично рас- · · · положенными максимумами второго ~ ' · порядка равны Ax = 60 мм (по оси х) · и Ay = 40 мм (по оси у). ' * .

135. Пучок рентгеновских лучей падает на трехмерную прямоуголь­ную решетку, периоды которой a, b Рис. 5.29. и с. Направление падающего пучка

совпадает с направлением, вдоль которого период решетки равен а. Найти направления на дифракционные максимумы и длины волн, при которых эти максимумы будут наблюдаться.

127. Узкий пучок рентгеновских лучей падает под углом сколь­жения а = 60, O^q на естественную грань монокристалла NaCl, плотность которого ρ = 2,16 г/см³. При зеркальном отражении от этой грани образуется максимум второго порядка. Определить длину волны излучения.

128. Пучок рентгеновских лучей с λ = 174 пм падает на по­верхность монокристалла, поворачивающегося вокруг оси, которая параллельна его поверхности и перпендикулярна к направлению падающего пучка. При этом направления на максимумы второго и третьего порядков от системы плоскостей, параллельных поверхно­сти монокристалла, образуют между собой угол а = 60°. Найти соответствующее межплоскостное расстояние.

129. При прохождении пучка рентгеновских лучей с X = = 17,8 пм через поликристаллический образец на экране, располо­женном на расстоянии / = 15 см от образца, образуется система дифракционных колец. Определить радиус светлого кольца, соответ­ствующего второму порядку отражения от системы плоскостей с межплоскостным расстоянием d = 155 пм.

5.4. Поляризация света

φ Степень поляризации света:

P ₌ /макс- /мин _{а (5 4а)} /макс"ι 'мин

φ Закон Малюса:

JS

/ = Z₀Cos² φ. ffe,- (5.46)

φ Закон Брюстера:

^n₂In₁. (5.4в)

φ Формулы Френеля для интенсивности света, отраженного от границы раздела двух диэлектриков:

где Z₁ и — интенсивности падающего света, у которого колебания светового вектора соответственно перпендикулярны и параллельны плоскости падения.

6 = (26 + 1) π

φ Кристаллическая пластинка между двумя поляризаторами P и P^f, Если угол между плоскостью поляризатора P и оптической осью OO' пластинки равен 45°, то интенсивность /' света, прошедшего через поляризатор P', оказы­вается максимальной или минимальной при следующих условиях:

поляризаторы PwP' b — 2nk

<5.4д)

/;' = мин j *

ίι~ макс-

/)| = макс / 1 = мин

параллельны скрещены

Здесь 6 = 2л: (/г₀ — п^) ^ί/λ — разность фаз между обыкновенным и необыкно­венным лучами, fc —0, 1, 2, ...

φ Естественное и магнитное вращение плоскости поляризации:

(р_ест = αί, фнагн = VlH₉ (5.4е)

где а —постоянная вращения, V—постоянная Верде,

127. Плоская монохроматическая волна естественного света с интенсивностью I₀ падает нормально на экран из двух соприкаса­ющихся поляроидных полуплоскостей. Главное направление одного поляроида параллельно, а другого перпендикулярно к границе раз­дела поляроидов. Какой характер имеет дифракционная картина за экраном? Какова интенсивность света за экраном в точках плоско­сти, перпендикулярной к экрану и проходящей через границу раздела поляроидов?

128. Плоская монохроматическая волна естественного, света с интенсивностью I₀ падает нормально на непрозрачный экран с круг­лым отверстием, которое представляет собой первую зону Френеля для точки наблюдения Р. Найти интенсивность света в точке P после того, как отверстие перекрыли двумя одинаковыми полярои­дами, главные направления которых перпендикулярны друг к другу, а граница их раздела проходит:

а) по диаметру отверстия;

б) по окружности, ограничивающей первую половину зоны Френеля.

127. Линейно поляризованный световой пучок падает на поля­ризатор, вращающийся вокруг оси пучка с угловой скоростью ω = 21 рад/с. Найти световую энергию, проходящую через поляри­затор за один оборот, если поток энергии в падающем пучке Ф₀ = - 4,0 мВт.

128. Пучок естественного света падает на систему из Af = 6 николей, плоскость пропускания каждого из которых повернута на угол φ = 30° относительно плоскости пропускания предыдущего никол я. Какая часть светового потока проходит через эту си­стему?

129. Естественный свет падает на систему из трех последова­тельно расположенных одинаковых поляроидов, причем главное направление среднего поляроида составляет угол φ == 60° с глав­ными направлениями двух других поляроидов. Каждый поляроид обладает поглощением таким, что при падении на него линейно поляризованного света максимальный коэффициент пропускания составляет τ = 0,81. Во сколько раз уменьшится интенсивность света после прохождения этой системы?

130. Степень поляризации частично поляризованного света P = 0,25. Найти отношение интенсивности поляризованной состав­ляющей этого света к интенсивности естественной составляющей.

131. На пути частично поляризованного пучка поместили николь. При повороте николя на угол φ = 60° из положения, соот­ветствующего максимуму пропускания света, интенсивность про­шедшего света уменьшилась в η — 3,0 раза. Найти степень поляри­зации падающего света.

132. На пути естественного пучка света поместили два несо­вершенных одинаковых поляризатора. Оказалось, что при парал­лельных плоскостях поляризаторов эта система пропускает в η - = 10,0 раза больше света, чем при скрещенных плоскостях. Найти степень поляризации света, которую со­здает:

а) каждый поляризатор в отдельности;

б) вся система при параллельных плоскостях поляризаторов.

127. Два параллельных одинако­вых по интенсивности линейно поляри­зованных пучка, плоскости колебаний которых N_x и N₂ повернуты относительно друг друга на некоторый малый угол φ (рис. 5.30), падают на николь. Для уравнивания интенсивностей обоих пуч­ков за николем его главное направление N должно быть установ­лено по биссектрисе А или 5. Определить значение угла φ, при котором поворот николя из положения А на малый угол δφ φ приводит к относительному изменению интенсивностей обоих пуч­ков Al/1 на величину в η = 100 раз большую* чем при повороте на тот же угол из положения β.

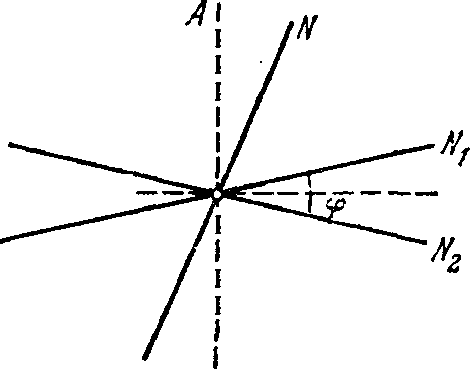
127. β

     Рис. 5.30.

     Показать с помощью формул Френеля, что отраженный от поверхности диэлектрика свет будет полностью поляризован, если угол падения A₁ удовлетворяет условию tg = я, где η — показатель преломления диэлектрика. Каков при этом угол между отраженным и преломленным лучами?

128. Естественный свет падает под углом Брюстера на поверх­ность стекла. Определить с помощью формул Френеля:

а) коэффициент отражения;

б) степень поляризации преломленного света.

127. Плоский пучок естественного света с интенсивностью I₀ падает под углом Брюстера на поверхность воды. При этом ρ = = 0,039 светового потока отражается. Найти интенсивность прелом­ленного пучка.

128. На поверхность воды под углом Брюстера падает пучок плоскополяризованного света. Плоскость колебаний светового век­тора составляет угол φ = 45° с плоскостью падения. Найти коэф­фициент отражения.

129. Узкий пучок естественного света падает под углом Брю­стера на поверхность толстой плоскопараллельной прозрачной пла­стины. При этом от верхней поверхности отражается ρ = 0,080 светового потока. Найти степень поляризации пучков 1—4 (рис. 5.31).

5.171. На плоскопараллельную стек­лянную пластинку (см. рис. 5.31) падает под углом Брюстера узкий пучок света интенсивности /₀. Определить с помощью формул Френеля:

а) интенсивность прошедшего пуч­ка /₄, если падающий свет линейно поля­ризован, причем плоскость колебаний его перпендикулярна к плоскости падения;

б) степень поляризации прошедшего через пластинку пучка, если падающий свет — естественный.

172. Узкий пучок естественного света падает под углом Брю­стера на стопу Столетова, состоящую из N толстых плоскопарал­лельных стеклянных пластин. Найти:

а) степень поляризации P прошедшего пучка;

б) чему равно P при N = 1, 2, 5 и 10.

172. Определить с помощью формул Френеля:

а) коэффициент отражения естественного света при нормальном падении на поверхность стекла;

б) относительную потерю светового потока за счет отражений при прохождении параксиального пучка естественного света через центрированную оптическую систему из пяти стеклянных линз (вторичными отражениями света пренебречь).

172. Световая волна падает нормально на поверхность стекла, покрытого слоем прозрачного вещества. Пренебрегая вторичными отражениями, показать, что амплитуды световых волн, отраженных от обеих поверхностей такого слоя, будут одинаковы при условии

Рис. 5.3f.

п' = Уп, где п! я η — показатели преломления слоя и стекла соот­ветственно.

172. На поверхность стекла падает пучок естественного света. Угол падения равен 45°. Найти с помощью формул Френеля степень поляризации:

а) отраженного света; б) преломленного света.

172. Построить по Гюйгенсу волновые фронты и направления распространения обыкновенного и необыкновенного лучей в поло­жительном одноосном кристалле, оптическая ось которого:

а) перпендикулярна к плоскости падения и параллельна поверх­ности кристалла;

б) лежит в плоскости падения и параллельна поверхности кри­сталла;

в) лежит в плоскости падения под углом 45° к поверхности кристалла, и свет падает перпендикулярно к оптической оси.

172. Узкий пучок естествен­ного света с длиной волны λ = = 589 нм падает нормально на поверхность призмы Волластона, сделанной из исландского шпата, как показано на рис. 5.32. Опти­ческие оси обеих частей призмы взаимно перпендикулярны. Найти угол δ между направлениями пуч­ков за призмой, если угол θ = 30°.

173. Какой характер поляри­зации имеет плоская электромаг­нитная волна, проекции вектора E которой на оси χ и у, перпендику­лярные к направлению ее распространения, определяются следу­ющими уравнениями:

а) E_x = E cos (ωί — kz), E_y = E sin (ωί — kz)\

б) E_x = E cos (ωί — fez), E_y = E cos (ωί — kz + я/4);

в) E_x = E cos (ωί — kz), E_y = E cos (ωί — kz + я)?

172. Требуется изготовить параллельную оптической оси квар­цевую пластинку, толщина которой не превышала бы 0,50 мм. Найти максимальную толщину этой пластинки, при которой линейно поля­ризованный свет с длиной волны λ — 589 нм после прохождения ее:

а) испытывает лишь поворот плоскости поляризации;

б) станет поляризованным по кругу.

172. Кварцевую пластинку, вырезанную параллельно оптиче­ской оси, поместили между двумя скрещенными николями. Угол между главными направлениями николей и пластинки равен 45°. Толщина пластинки d = 0,50 мм. При каких длинах волн в интер­вале 0,50—0,60 мкм интенсивность света, прошедшего через эту систему, не будет зависеть от поворота заднего николя? Разность показателей преломления обыкновенных и необыкновенных лучей в этом интервале длин волн считать Δη = 0,0090.

172. Белый естественный свет падает на систему из двух скре­щенных николей, между которыми находится кварцевая пластинка,

173. вырезанная параллельно оптической оси, толщиной 1,50 мм. Ось пластинки составляет угол 45° с главными направлениями николей. Прошедший через эту систему свет разложили в спектр. Сколько тем­ных полос будет наблюдаться в интервале длин волн 0,55—0,66 мкм? Разность показателей преломления обыкновенных и необыкновен­ных лучей в этом интервале длин волн считать равной 0,0090.

174. Кристаллическая пластинка, вырезанная параллельно оптической оси, имеет толщину 0,25 мм и служит пластинкой в чет­верть волны для λ — 530 нм. Для каких длин волн в области види­мого спектра она будет также пластинкой в четверть волны? Считать, что для всех длин волн видимого спектра разность показателей пре­ломления обыкновенных и необыкновенных лучей одинакова и равна п_е — п₀ = 0,0090.

175. Кварцевая пластинка, вырезанная параллельно оптиче­ской оси, помещена между двумя скрещенными николями так, что ее оптическая ось составляет угол 45° с главными направлениями николей. При какой минимальной толщине пластинки свет с λ_χ = = 643 нм будет проходить через эту систему с максимальной интен­сивностью, а свет с λ₂ = 564 нм будет сильно ослаблен? Разность показателей преломления обыкновенных и необыкновенных лучей для обеих длин волн считать равной rt_e — п₀ = 0,0090.

176. Между двумя скрещенными поляроидами поместили квар­цевый клин с преломляющим углом θ = 3,5°. Оптическая ось клина параллельна его ребру и составляет угол 45° с главными направле­ниями поляроидов. При прохождении через эту систему света с λ — 550 нм наблюдается система интерференционных полос. Ширина каждой полосы Ax = 1,0 мм. Определить разность показа­телей преломления кварца для необыкновенного и обыкновенного лучей указанной длины волны.

177. Естественный монохроматический свет интенсивности I₀ падает на систему #з двух поляроидов, между которыми находится кристаллическая пластинка, вырезанная параллельно оптической оси. Пластинка вносит разность фаз δ между обыкновенным и не­обыкновенным лучами. Показать, что интенсивность света, прошед­шего через эту систему,

I = ¹Z₂Z₀ [cos² (φ — φ') — sin 2φ ■ sin 2φ' · sin² (δ/2)],

где φ и φ' — углы между оптической осью кристалла и главными направлениями поляроидов. Рассмотреть, в частности, случаи скре­щенных и параллельных поляроидов.

172. Монохроматический поляризованный по кругу свет па­дает нормально на кристаллическую пластинку, вырезанную па­раллельно оптической оси. За пластинкой находится николь, глав­ное направление которого составляет угол φ с оптической осью пластинки. Показать, что интенсивность света, прошедшего через эту систему,

/ = I₀ (1 + sin 2φ · sin δ),

где δ — разность фаз между обыкновенным и необыкновенным лу­чами, которую вносит пластинка.

172. Как с помощью поляроида и пластинки в четверть волны, изготовленной из положительного одноосного кристалла (п_е > п₀), отличить:

а) свет левополяризованный по кругу от правополяризованного; . б) естественный свет от поляризованного по кругу и от смеси естественного света с поляризованным по кругу?

172. Свет с длиной волны λ падает на систему из скрещенных поляризатора Я и анализатора Л, между которыми находится ком­пенсатор Бабине/С(рис. 5.33). Компен­сатор состоит из двух кварцевых клиньев, оптическая ось одного из которых параллельна ребру клина, другого — перпендикулярна к нему. Главные направления поляризатора н анализатора составляют угол 45° с оптическими осями компенсатора. Известны также преломляющий угол θ Клиньев (θ 1) и разность показа­телей преломления кварца п_е — п₀. При введении исследуемого двупре- ломляющего образца О (его оптиче­ская ось ориентирована так, как показано на рисунке) наблюдае­мые интерференционные полосы сдвинулись вверх на δχ мм. Найти:

а) ширину интерференционной полосы Ах;

б) величину и знак оптической разности хода обыкновенного и необыкновенного лучей, которую вносит образец О.

172. Вычислить с помощью таблиц приложения разность по­казателей преломления кварца для право- и левополяризованного по кругу света с длиной волны λ — 589,5 нм.

173. Линейно поляризованный свет с длиной волны 0,59 мкм падает на трехгран­ную кварцевую призму Π (рис. 5.34) с пре­ломляющим углом θ = 30°. В призме свет распространяется вдоль оптической оси, направление которой показано штриховкой. За поляроидом P наблюдают систему свет­лых и темных полос, ширина которых Δ* = 15,0 мм. Найти постоянную враще­ния кварца, а также характер распределе­ния интенсивности света за поляроидом.

174. о

     к

     π

     Рис. 5.33.

     

     Естественный монохроматический свет падает на систему из двух скрещенных николей, между которыми находится кварце­вая пластинка, вырезанная перпендикулярно к оптической оси. Найти минимальную толщину пластинки, при которой эта система будет пропускать η = 0,30 светового потока, если постоянная вра­щения кварца а = 17 угл.град/мм.

175. Свет проходит через систему из двух скрещенных николей, между которыми расположена кварцевая пластинка, вырезанная перпендикулярно к оптической оси. Определить минимальную толщину пластинки, при которой свет с длиной волны 436 нм будет полностью задерживаться этой системой, а свет с длиной волны 497 нм — пропускаться наполовину. Постоянная вращения кварца для этих длин волн равна соответственно 41,5 и 31,1 угл.град/мм.

176. Линейно поляризованный свет с длиной волны 589 нм проходит вдоль оси цилиндрического стеклянного сосуда, заполнен­ного слегка замутненным раствором сахара с концентрацией 500 г/л. При наблюдении сбоку видна система винтообразных полос, причем расстояние между соседними темными полосами вдоль оси равно 50 см. Объяснить возникновение полос и определить удельную постоянную вращения раствора.

177. Ячейку Keppa поместили между двумя скрещенными николями так, что направление электрического поля E в конденса­торе образует угол 45° с главными направлениями николей. Конден­сатор имеет длину / = 10 см и заполнен нитробензолом. Через систему проходит свет с λ = 0,50 мкм. Имея в виду, что в данном случае постоянная Keppa В = 2,2 -10"¹⁰ см/В², определить:

а) минимальную напряженность электрического поля E в кон­денсаторе, при которой интенсивность света, прошедшего через эту систему, не будет зависеть от поворота заднего николя;

б) число прерываний света в одну секунду, если на конденсатор подать синусоидальное напряжение с частотой ν = 10 МГц и ампли­тудным значением напряженности E_m = 50 кВ/см.

Примечание. Постоянной Keppa называют-коэффициент В в формуле п_е — п₀ = B^fKE²ⁱ.

172. Монохроматический плоскополяризованный свет с круго­вой частотой ω проходит через вещество вдоль однородного магнит­ного поля с'напряженностью Н. Найти разность показателей пре­ломления для право- и левополяризованных по кругу компонент светового пучка, если постоянная Верде равна У.

173. Некоторое вещество поместили в продольное магнитное поле соленоида, расположенного между двумя поляроидами. Длина трубки с веществом I = 30 см. Найти постоянную Верде, если при напряженности поля H = 56,5 кА/м угол поворота плоскости поля­ризации φ_χ = +5°10' для од­ного направления поля и

P φ₂ = —3°20' для противопо- 6 ложного направления поля. ^ 5.197. Узкий пучок плос-

кополяризованного света про­ходит через правовращающее положительное вещество, на­ходящееся в ^ продольном магнитном поле, как показано на рис. 5.35. Найти угол, на который повернется плоскость поля­ризации вышедшего пучка, если длина трубки с веществом равна I₉

его постоянная вращения α, постоянная Верде V и напряженность магнитного поля Я.

198. Трубка с бензолом длины / = 26 см находится в продоль­ном магнитном поле соленоида, расположенного между двумя поля­роидами. Угол между главными направлениями поляроидов равен 45°. Найти минимальную напряженность магнитного поля, при ко­торой свет с длиной волны 589 нм будет проходить через эту систему только в одном направлении (оптический вентиль). Как будет вести себя этот оптический вентиль, если изменить направление данного магнитного поля на противоположное?

199. Опыт показывает, что телу, облучаемому поляризованным по кругу светом, сообщается вращательный момент (эффект Садов­ского). Это связано с тем, что данный свет обладает моментом им­пульса, плотность потока которого в вакууме M = У/со, где I — интенсивность света, со — его круговая частота колебаний. Пусть поляризованный по кругу свет с длиной волны λ = 0,70 мкм падает нормально на однородный черный диск массы т = 10 мг, который может свободно вращаться вокруг своей оси. Через сколько вре­мени его угловая скорость станет ω₀ = 1,0рад/с, если / = 10Вт/см²?

5.5. Дисперсия и поглощение света

φ Согласно элементарной теории дисперсии диэлектрическая проницаемость вещества:

k

где Tif_i- концентрация электронов с собственной частотой ω₀&·

φ Связь между показателем преломления и диэлектрической проницае­мостью вещества:

ω άω

^υ=~τ> ^и = нь' (⁵·^5ε)

η=V ε. (5.56)

φ Фазовая ν и групповая и скорости:

ω __

T^{9 u}^dk

φ Формула Рэлея:

ι dv - _v

u = v — X . (ь.5г)

φ Закон ослабления узкого пучка электромагнитного излучения:

/ = /₀е-д</, (5.5д)

где μ = κ + κ', μ, κ, κ' —линейные показатели ослабления, поглощения и рассеяния.

5.200. Свободный электрон находится в поле монохроматической световой волны. Интенсивность света / = 150 Вт/м², его частота ω = 3,4 ·10¹⁵ рад/с. Найти:

а) амплитуду колебаний электрона и амплитуду его скорости;

б) отношение FJ F_%, где F_vi и F₃ —амплитудные значения сил, действующих на электрон со стороны магнитной и электрической составляющих поля световой волны; показать также, что это отно­шение равно V₂ v/c, где ν — амплитуда скорости электрона, с — скорость света.

Указание. В уравнении движения электрона можно не учи­тывать действие магнитной составляющей поля (как будет видно из расчета, оно пренебрежимо мало).

5.201» Электромагнитная волна с частотой ω распространяется в разреженной плазме. Концентрация свободных электронов в плаз­ме равна п₀. Пренебрегая взаимодействием волны с ионами плазмы, найти зависимость:

а) диэлектрической проницаемости плазмы от частоты;

б) фазовой скорости электромагнитной волны от ее длины волны λ в плазме.

202. Найти концентрацию свободных электронов ионосферы, если для радиоволн с частотой ν — 100 МГц ее показатель прелом­ления η = 0,90.

203. Имея в виду, что для достаточно жестких рентгеновских лучей электроны вещества можно считать свободными, определить, на сколько отличается от единицы показатель преломления графита для рентгеновских лучей с длиной волны в вакууме λ — 50 пм.

204. Электрон, на который действует квазиупругая сила kx и «сила трения» γχ, находится в поле электромагнитного излучения, E-составляющая поля —меняется во времени по закону E = £₀cos со/. Пренебрегая действием магнитной составляющей поля, найти:

а) уравнение движения электрона;

б) среднюю мощность, поглощаемую электроном; частоту, при которой она будет максимальна, и выражение для максимальной сред­ней мощности.

202. В ряде случаев диэлектрическая проницаемость вещества оказывается величиной комплексной или отрицательной и показа­тель преломления — соответственно комплексным {η' = η + ίκ) или чисто мнимым (n' ~ ίκ). Написать для этих случаев уравнение

плоской волны и выяснить физи­ческий смысл таких показателей преломления.

202. При зондировании разре­женной плазмы радиоволнами раз­личных частот обнаружили, что радиоволны с λ > λ₀ = 0,75 м ис­пытывают полное внутреннее отра­жение. Найти концентрацию сво­бодных электронов в этой плазме.

203. 

     Рис. 5.36.

     Исходя из определения групповой скорости и, получить формулу Рэлея (5.5г). Показать также, что и вблизи λ = λ' равна отрезку ν', отсекаемому каса­тельной к кривой ν (λ) в точке λ' (рис. 5.36).

204. Найти зависимость между групповой и и фазовой ν ско­ростями для следующих законов дисперсии:

а) ν r^j 1 /]/Т;

б) ν k\

в) ν г^ 1/ω².

Здесь λ, k и ω — длина волны, волновое число и круговая частота.

202. В некоторой среде связь между групповой и фазовой ско­ростями электромагнитной волны имеет вид uv = с², где с — ско­рость света в вакууме. Найти зависимость диэлектрической прони­цаемости этой среды от частоты волны, ε (со).

203. Показатель преломления сероуглерода для света с дли­нами волн 509, 534 и 589 нм равен соответственно 1,647, 1,640 и 1,630. Вычислить фазовую и групповую скорости света вблизи λ = 534 нм.

204. Плоский световой импульс распространяется в среде, где фазовая скорость ν линейно зависит от длины волны λ по закону ν ~ а ЬХ_У а я b — некоторые положительные постоянные. Пока­зать, что в такой среде форма произвольного светового импульса будет восстанавливаться через промежуток времени τ = 1 /b.

205. Пучок естественного света интенсивности I₀ падает на систему из двух скрещенных николей, между которыми находится трубка с некоторым раствором в продольном магнитном поле напря­женности Я. Длина трубки /, линейный показатель поглощения раствора κ и постоянная Верде V. Найти интенсивность света, про­шедшего через эту систему.

206. Плоская монохроматическая световая волна с интенсив­ностью /₀ падает нормально на плоскопараллельную пластинку, коэффициент отражения каждой поверхности которой равен р. Учтя многократные отражения, найти интенсивность прошедшего света, если:

а) пластинка идеально прозрачная (поглощение отсутствует);

б) линейный показатель поглощения равен κ, а толщина пла­стинки d.

202. Из некоторого вещества изготовили две пластинки: одну толщиной d_t = 3,8 мм, другую — 4> = 9,0 мм. Введя поочередно эти пластинки в пучок монохроматического света, обнаружили, что первая пластинка пропускает T₁ = 0,84 светового потока, вто­рая — T₂ = 0,70. Найти линейный показатель поглощения этого вещества. Свет падает нормально. Вторичными отражениями пре­небречь.

203. 225

     Монохроматический пучок проходит через стопу из Af = 5 одинаковых плоскопараллельных стеклянных пластинок каждая толщиной / = 0,50 см. Коэффициент отражения на каждой поверх­ности пластинок ρ = 0,050. Отношение интенсивности света, про­шедшего через эту стопу пластинок, к интенсивности падающего света τ = 0,55. Пренебрегая вторичными отражениями света, опре­делить показатель поглощения данного стекла.

8 И. Е. Иродов

202. Монохроматический пучок света падает нормально на поверхность плоскопараллельной пластины толщины I, Показатель поглощения вещества пластины линейно изменяется вдоль нормали к ее поверхности от значения X₁ до κ₂. Коэффициент отражения от каждой поверхности пластины равен р. Пренебрегая вторичными отражениями, определить коэффициент пропускания такой пла­стины.

203. Пучок света интенсивности I₀ падает нормально на пло­скопараллельную прозрачную пластинку толщины L Пучок содер­жит все длины волн в диапазоне от λ_χ до λ₂ одинаковой спектральной интенсивности. Определить интенсивность прошедшего через пла­стинку пучка, если в этом диапазоне длин волн показатель поглоще­ния линейно зависит от λ в пределах от X₁ до κ₂ и коэффициент отра­жения каждой поверхности равен р. Вторичными отражениями пренебречь.

204. Светофильтр представляет собой пластинку толщины d с показателем поглощения, зависящим от длины волны λ по формуле

κ (λ) = сс (1—λ/λ₀)² см"¹,

где ос и λ₀ — некоторые постоянные. Найти ширину полосы про­пускания этого светофильтра Δλ — ширину, при которой ослаб­ление света на краях полосы в η раз больше, чем ослабление при λ₀. Коэффициент отражения от поверхностей светофильтра счи­тать одинаковым для всех длин волн.

202. Точечный монохроматический источник, испускающий световой поток Ф, находится в центре сферического слоя вещества, внутренний радиус которого равен а, наружный — Ь. Линейный показатель поглощения вещества равен κ, коэффициент отражения поверхностей —р. Пренебрегая вторичными отражениями, найти интенсивность света на выходе из этого вещества.

203. Во. сколько раз уменьшится интенсивность узкого пучка рентгеновского излучения с длиной волны 20 пм при прохожде­нии свинцовой пластинки толщины ^= 1,0 мм, если массовый показатель ослабления для данной длины волны излучения μ/ρ = 3,6 см²/г?

204. Узкий пучок рентгеновского излучения с длиной волны 62 пм проходит через алюминиевый экран толщины 2,6 см. Какой толщины надо взять свинцовый экран, чтобы он ослаблял данный пучок в такой же степени? Массовые показатели ослабления алюми­ния и свинца для этого излучения равны соответственно 3,48 и 72,0 см²/г.

205. Найти для алюминия толщину слоя половинного ос­лабления узкого пучка монохроматического рентгеновского излучения, если соответствующий массовый показатель ослабления μ/ ρ = 0,32 см²/г.

206. Сколько слоев половинного ослабления в пластинке, которая уменьшает интенсивность узкого пучка рентгеновского из­лучения в η = 50 раз?

5.6. Оптика движущихся источников

φ Эффект Доплера при и

Αω ν * /е л ν

— costh (5.6а)

ω с

где и —скорость источника, ft — угол между направлением движения источника и линией наблюдения.

φ Эффект Доплера в общем случае:

(D=O)₀ ππτ. (⁵-⁶⁶)

⁰ 1 — β COS XT '

где β = с/с.

Φ При O- = O эффект Доплера называют продольным, при ft = π/2 — попе­речным.

φ Эффект Вавилова —Черенкова:

cos ft = — , (5.6в)

ην '

где ft —угол между направлением распространения излучения и вектором скорости ν частицы.

202. В опыте Физо по определению скорости света расстояние между зубчатым колесом и зеркалом I = 7,0 км, число зубцов ζ = = 720. Два последовательных исчезновения света наблюдали при скоростях вращения колеса п_х = 283 об/с и n₂ = 313 об/с. Найти скорость света.

203. Источник света движется со скоростью ν относительно приемника. Показать, что при ν с относительное изменение ча­стоты света определяется формулой (5.6а).

204. Одна из спектральных линий, испускаемых возбужден­ными ионами He⁺, имеет длину волны λ = 410 нм. Найти доплеров- ское смещение Δλ этой линии, если ее наблюдать под углом Oⁱ = 30^q к пучку движущихся ионов с кинетической энергией T= 10 МэВ.

205. При наблюдении спектральной линии λ = 0,59 мкм в на­правлениях на противоположные края солнечного диска на его эк­ваторе обнаружили различие в длинах волн на δλ = 8,0 пм. Найти период вращения Солнца вокруг собственной оси.

206. Эффект Доплера позволил открыть двойные звезды столь удаленные, что разрешение их с помощью телескопа оказалось не­возможным. Спектральные линии таких звезд периодически стано­вятся двойными, из чего можно предположить, что источником яв­ляются две звезды, обращающиеся вокруг их центра масс. Считая массы обеих звезд одинаковыми, найти расстояние между ними и их массы, если максимальное расщепление спектральных линий равно (AXfk)_m = 1,2· 10"⁴, причем оно возникает через каждые τ = 30 дней.

207. Плоская электромагнитная волна частоты со₀ падает нор­мально на поверхность зеркала, движущегося навстречу с реляти­вистской скоростью V. Воспользовавшись формулой Доплера,

8* 227

найти частоту отраженной волны. Упростить полученное выражение для случая V <<; с.

202. Радиолокатор работает на длине волны λ = 50,0 см. Определить скорость приближающегося самолета, если частота бие­ний между сигналом передатчика и сигналом, отраженным от само­лета, в месте расположения локатора равна Δν = 1,00 кГц.

203. Имея в виду, что фаза волны со/— kx есть инвариант, т. е. не меняется при переходе от одной инерциальной системы к дру­гой, определить, как преобразуются входящие в нее частота ω и волновое число /г. Рассмотреть одномерный случай.

204. С какой скоростью удаляется от нас некоторая туман­ность, если известно, что линия водорода λ = 434 нм в ее спектре смещена в красную сторону на 130 нм?

205. С какой скоростью должна была бы двигаться автома­шина, чтобы красный свет светофора (λ « 0,70 мкм) превратился в зеленый (λ' « 0,55 мкм)?

206. По некоторой прямой движутся в одном направлении на­блюдатель со скоростью V₁ = Y₂ с и впереди него источник монохро­матического света со скоростью V₂ = ³/₄с. Собстветшатгчастота света равна CO₀. Найти частоту света, которую зафиксирует наблюдатель.

207. Одна из спектральных линий атомарного водорода имеет длину волны λ = 656,3 нм. Найти доплеровское смещение этой ли­нии Δλ, если ее наблюдать под прямым уг-

0 ^_m лом к пучку атомов водорода с кинетиче-

1. ской энергией T = 1,0 МэВ (поперечный ρ доплер-эффект).

j 5.236. Источник, испускающий электро-

I магнитные сигналы с собственной частотой

" со₀ — 3,0* 10¹⁰ рад/с, движется с постоян-

Рис. 5.37. ной скоростью ν = 0,80 с по прямой, от­

стоящей от неподвижного наблюдателя P на расстоянии I (рис. 5.37). Найти частоту сигналов, воспринимае­мых наблюдателем в момент, когда:

а) источник окажется в точке О;

б) наблюдатель увидит его в точке О.

5.237. Узкий пучок электронов проходит непосредственно над поверхностью металлического зеркала, на котором нанесена диф­ракционная решетка с периодом ν d — 2,0 мкм. Электроны движутся со скоростью ν, близкой к C_t пер- пендикулярно к штрихам решетки. ^лр _v При этом наблюдается видимое

штшкт>т>_?ш: излучение - траектория электро­нов имеет вид полоски, окраска

Рис. 5.38. которой меняется в зависимости от

угла наблюдения Oⁱ (рис. 5.38). Объяснить это явление. Найти дайну волны наблюдаемого из­лучения при Φ = 45°.

238. Газ состоит из атомов массы т> находящихся в термодина­мическом равновесии при температуре T. Пусть ω₀ — собственная частота излучаемого атомами света.

а) Показать, что спектральное распределение излучаемого света определяется формулой

J / α—α(I—ω/ω₀)²

¹ ω —'¹ о^с >

(/₀ — спектральная интенсивность, соответствующая частоте ω_0> а = nw²/2kT).

б) Найти относительную ширину Δω/ω₀ данной спектральной линии, т. е. ширину линии между частотами, при которых Ι_ω = IJ2.

238. В среде, движущейся с постоянной скоростью V <; с относительно инерциальной /(-системы, распространяется плоская электромагнитная волна. Найти скорость этой волны в /С-системе, если показатель преломления среды равен η и направление распро­странения волны совпадает с направлением движения среды.

239. Аберрация света заключается в том, что при наблюдении звезды кажутся смещенными от истинного положения на небосводе (из-за движения Земли по орбите). Направление на звезду в плоско­сти эклиптики периодически меняется, и звезда совершает кажу­щиеся колебания в пределах угла δθ = 41". Найти скорость Земли на орбите.

240. Показать, что преобразование угла ft между направле­нием распространения света и осью χ при переходе от К- к К -си­стеме отсчета определяется формулой

_η α, cos Φ—β

cos V^t =S _Ί—5—-α,

1 — β cos ν

где β = V/c_y V — скорость /('-системы относительно /(-системы. Оси χ и х^г обеих систем отсчета совпадают.

238. Найти угол полураствора конуса, в котором будут видны звезды, расположенные в полусфере для земного наблюдатели, если двигаться относительно Земли с релятивистской скоростью V_t отличающейся от скорости света на 1,0%. Воспользоваться форму­лой из предыдущей задачи.

239. Найти условия, при которых заряженная частица, движу­щаяся равномерно в среде с показателем преломления /г, будет излу­чать свет (эффект Вавилова — Черенкова). Найти также направле­ние этого излучения.

Указание. Рассмотреть интерференцию колебаний, воз­буждаемых частицей в разные моменты времени.

238. Найти наименьшие значения кинетической энергии элек­трона и протона, при которых возникает черенковское излучение в среде с показателем преломления η = 1,60. Для каких частиц это значение кинетической энергии 7\_шн = 29,6 МэВ?

239. Определить кинетическую энергию электронов, которые в среде с показателем преломления η = 1,50 излучают свет под углом Φ = 30° к направлению своего движения.

5.7. Тепловое излучение. Квантовая природа света

Φ Энергетическая светимость:

M₃ = -^-U, (5.7а)

где и —объемная плотность энергии теплового излучения. Φ Формула Вина и закон смещения Вииа:

«ω = (ω/Γ), TK_m - b, (5.76)

где X_m—длина волны, соответствующая максимуму функции и Φ Закон Стефана — Больцмана:

M_a = σΤ*, (5.7в)

где σ — постоянная Стефаиа — Больцмана. Φ Формула Планка:

1

"ω"—^TferZl · (5.7г)

Φ Формула Эйнштейна для фотоэффекта:

^mvI_taKC

П<о=А + (5.7д)

Φ Эффект Комптона:

Δλ=2πλ₀ (1 —cos θ), j[5.7e)

где ^_c = Itjmc—комптоновская длииа волны.

238. Показать с помощью формулы Вина, что

а) наиболее вероятная частота излучения о_вер со Г;

б) максимальная спектральная плотность теплового излучения

(Омакс Г³;

в) энергетическая светимость M_a с\э T*⁴.

238. Имеется два абсолютно черных источника теплового излу­чения. Температура одного из них T₁ = 2500 К. Найти температуру другого источника, если длина волны, отвечающая максимуму его испускательной способности, на Δλ = 0,50 мкм больше длины вол­ны, соответствующей максимуму испускательной способности пер­вого источника.

239. Энергетическая светимость абсолютно черного тела M_a = = 3,0 Вт/см². Определить длину волны, отвечающую максимуму испускательной способности этого тела.

240. Излучение Солнца по своему спектральному составу близко к излучению абсолютно черного тела, для которого макси­мум испускательной способности приходится на длину волны 0,48 мкм. Найти массу, теряемую Солнцем ежесекундно за счет излучения. Оценить время, за которое масса Солнца уменьшится на 1%.

241. Найти температуру полностью ионизованной водородной плазмы плотностью ρ = 0,10 г/см³, при которой давление теплового излучения равно газокинетическому давлению частиц плазмы.

Иметь в виду, что давление теплового излучения ρ = и/3, где а — объемная плотность энергии излучения, и что при высоких темпера­турах вещества подчиняются уравнению состояния идеальных газов.

5.251. Медный шарик диаметра d = 1,2 см поместили в отка­чанный сосуд, температура стенок которого поддерживается близ­кой к абсолютному нулю. Начальная температура шарика T₀ = = 300 К. Считая поверхность шарика абсолютно черной, найти, через сколько времени его темпе- радура уменьшится в η = 2,0 раза.

.2 45.252. Имеются две полости (рисг"5.39) с малыми отверстиями одинаковых диаметров d = 1,0 см и абсолютно отражающими наруж­ными поверхностями. Расстояние

между отверстиями I = 10 см. В полости 1 поддерживается по­стоянная температура T₁ = 1700 К- Вычислить установившуюся температуру в полости 2.

Указание. Иметь в виду, что абсолютно черное тело явля­ется косинусным излучателем.

253. Полость объемом V = 1,0 л заполнена тепловым излуче­нием при температуре T = 1000 К. Найти:

а) теплоемкость C_v; б) энтропию S этого излучения.

253. Считая, что спектральное распределение энергии тепло­вого излучения подчиняется формуле_чВина α (ω, Τ) = Асо³е^_а(й/^г, где а = 7,64 пс· К/рад, найти для температуры T = 2000 К наибо­лее вероятную:

а) частоту излучения; б) длину волны излучения.

253. Получить с помощью формулы Планка приближенные выражения для объемной спектральной плотности излучения α_ω:

а) в области, где йсо ^ kT (формула Рэлея — Джинса);

б) в области, где йсо kT (формула Вина).

253. Преобразовать формулу Планка для объемной спектраль­ной плотности излучения α_ω от переменной ω к переменным ν (ли­нейная частота) и λ (длина волны).

254. Найти с помощью формулы Планка мощность излучения единицы поверхности абсолютно черного тела, приходящегося на узкий интервал длин волн Δλ = 1,0 нм вблизи максимума спек­тральной плотности излучения, при температуре тада/Т = 3000 K- X STSSS^Ha рис. 5.40 показан график функции ц(х)₉ которая ха­рактеризует относительную долю общей мощности теплового излу­чения, приходящуюся на спектральный интервал от 0 до х. Здесь χ = XfX_m (X_m — длина волны, отвечающая максимальной спек­тральной плотности излучения).

Найти с помощью этого графика:

а) длину волны, которая делит спектр излучения на две энерге­тически равные части при температуре 3700 К;

б) долю общей мощности излучения, которая приходится на видимую часть спектра (0,40—0,76 мкм) при температуре 5000 К;

в) во сколько раз увеличится мощность излучения в области длин волн λ > 0,76 мкм при возрастании температуры от 3000 до 5000 К.

У Dfi

О?

Dfi Dfi Dfi Dfi Dfi D₃I

О O₁Z Dfi Dfi Ofi Ifi Ifi Ifi Ifi Ifi^Zfi 2,2 Я Рис. 5.40.

259. Найти с помощью формулы Планка выражения, опреде­ляющие число фотонов в 1 см³ полости при температуре T в спект­ральных интервалах (ω, ω + άω) и (λ, λ + άλ).

260. Точечный изотропный источник испускает свет с I = = 589 нм. Световая мощность источника P = 10 Вт. Найти:

а) среднюю плотность потока фотонов на расстоянии г = 2,0 м от источника;

б) расстояние от источника до точки, где средняя концентра­ция фотонов η = 100 см"³.

259. Показать с помощью корпускулярных представлений, что импульс, переносимый в единицу времени плоским световым потоком, не зависит от его спектрального состава, а определяется только потоком энергии Ф₉.

260. Лазер излучил в импульсе длительностью τ = 0,13 мс пучок света с энергией E = 10 Дж. Найти среднее давление такого светового импульса, если его сфокусировать в пятнышко диаметром d = 10 мкм на поверхность, перпендикулярную к пучку, с коэффи­циентом отражения ρ = 0,50.

_f· 5.263. Короткий импульс света с энергией E = 7,5 Дж в виде узкого почти параллельного пучка падает на зеркальную пластинку с коэффициентом отражения ρ = 0,60. Угол падения Ό = 30°. Определить с помощью корпускулярных представлений импульс, переданный пластинке.

264. Плоская световая волна интенсивности / = 0,20 Bt/ci\i³ падает на плоскую зеркальную поверхность с коэффициентом отра­жения ρ = 0,8. Угол падения ft = 45°. Определить с помощью корпускулярных представлений значение нормального давления, которое оказывает свет на эту поверхность.

265. Плоская световая волна интенсивности / = 0,70 Вт/см² освещает шар с абсолютно зеркальной поверхностью. Радиус шара R = 5,0 см. Найти с помощью корпускулярных представлений силу светового давления, испытываемую шаром.

266. На оси круглой абсолютно зеркальной пластинки нахо­дится точечный изотропный источник, световая мощность которого Р. Расстояние между источником и пластинкой в η раз больше ее ра­диуса. Найти с помощью корпускулярных представлений силу све-- тового давления, испытываемую пластинкой.

267. В /(-системе отсчета фотон с частотой ω падает нормально на зеркало, которое движется ему навстречу с релятивистской скоро­стью V^r. Найти импульс, переданный зеркалу при отражении фотона:

а) в системе отсчета, связанной с зеркалом;

б) в /(-системе.

264. Небольшое идеально отражающее зеркальце массы т = = 10 мг подвешено на невесомой нити длины I = 10 см. Найти угол, на который отклонится нить, если по нормали к зеркальцу в горизонтальном направлении произвести «выстрел» коротким им­пульсом лазерного излучения с энергией E = 13 Дж. За счет чего зеркальце приобретет кинетическую энергию?

265. Фотон с частотой со₀ испущен с поверхности звезды, масса которой M и радиус R. Найти гравитационное смещение частоты фо­тона Δω/ω₀ на очень большом расстоянии от звезды.

266. При увеличении напряжения на рентгеновской трубке в η = 1,5 раза длина волны коротковолновой границы сплошного рентгеновского спектра изменилась на Δλ = 26 пм. Найти первона­чальное напряжение на трубке.

267. Узкий пучок рентгеновских лучей падает на монокри­сталл NaCl. Наименьший угол скольжения, при котором еще наб­людается зеркальное отражение от системы кристаллических пло­скостей с межплоскостным расстоянием d = 0,28 нм, равен α = 4,1^. Каково напряжение на рентгеновской трубке?

- 5.272. Найти длину волны коротковолновой границы сплошного рентгеновского спектра, если скорость электронов, подлетающих к антикатоду трубки, ν = 0,85с_у где с — скорость света.

273. Определить красную границу фотоэффекта для цинка и максимальную скорость фотоэлектронов, вырываемых с его поверх­ности электромагнитным излучением с длиной волны 250 нм.

274. При поочередном освещении поверхности некоторого ме­талла светом с длинами волн X₁ = 0,35 мкм и X₂ = 0,54 мкм обнару­жили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в η = 2,0 раза. Найти работу выхода с по­верхности этого металла.

275. До какого максимального потенциала зарядится удален­ный от других тел медный шарик при облучении его электромагнит­ным излучением с длиной волны λ = 140 нм?

276. Найти максимальную кинетическую энергию фотоэлектро­нов, вырываемых с поверхности лития электромагнитным излуче­нием, напряженность электрической составляющей которого ме­няется со временем по закону E = а (1 + cos со/) cos со₀/, где а — некоторая постоянная, ω = 6,0- IO¹⁴ рад/с и со₀ = 3,60· IO¹⁵ рад/с.

277. Электромагнитное излучение с длиной волны λ = 0,30 мкм падает на фотоэлемент, находящийся в режиме насыщения. Соот­ветствующая спектральная чувствительность фотоэлемента J = — 4,8 мА/Вт. Найти выход фотоэлектронов, т. е. число фотоэлек­тронов на каждый падающий фотон.

278. Имеется вакуумный фотоэлемент, один из электродов ко­торого цезиевый, другой — медный. Определить максимальную скорость фотоэлектронов, подлетающих к медному электроду, при освещении цезиевого электрода электромагнитным излучением с дли­ной волны 0,22 мкм, если электроды замкнуть снаружи накоротко.

279. Фототок, возникающий в цепи вакуумного фотоэлемента при освещении цинкового электрода электромагнитным излучением с длиной волны 262 нм, прекращается, если подключить внешнее задерживающее напряжение 1,5 В. Найти величину и полярность внешней контактной разности потенциалов данного фотоэлемента.

280. Составить выражение для величины, имеющей размер­ность длины, используя скорость света с, массу частицы т и постоян­ную Планка h. Что это за величина?

281. Показать с помощью законов сохранения, что свободный электрон не может полностью поглотить фотон.

282. Объяснить следующие особенности комптоновского рас­сеяния света веществом:

а) независимость смещения Δλ от природы рассеивающего вещества;

б) увеличение интенсивности смещенной компоненты рассеян­ного света с уменьшением атомного номера вещества, а также с ро­стом угла рассеяния;

в) наличие несмещенной компоненты в рассеянном излечении.

273. Узкий пучок монохроматического рентгеновского излу­чения падает на рассеивающее вещество. При этом длины волн излу­чения, рассеянного под углами O¹₁ = 60^q и Ф₂ = 120°, отличаются друг от друга в η — 2,0 раза. Считая, что рассеяние происходит на свободных электронах, найти длину волны падающего излучения.

274. Фотон с энергией Ηω = 1,00 МэВ рассеялся на свободном покоившемся электроне. Найти кинетическую энергию электрона отдачи, если в результате рассеяния длина волны фотона измени­лась на η = 25%.

275. Фотон с длиной волны λ — 6,0 пм рассеялся под прямым углом на покоившемся свободном электроне. Найти:

а) частоту рассеянного фотона;

б) кинетическую энергию электрона отдачи.

5.286. Фотон с энергией /ζω = 250 кэВ рассеялся под углом θ = 120° на первоначально покоившемся свободном электроне. Оп­ределить энергию рассеянного фотона.

5.287* Фотон с импульсом ρ = 1,02 МэВ/с, где с — скорость света, рассеялся на покоившемся свободном электроне, в результате чего импульс фотона стал p^r = 0,255 МэВ/с. Под каким углом рассе­ялся фотон?

288. Фотон рассеялся под углом O¹ = 120° на покоившемся свободном электроне, в результате чего электрон получил кинети­ческую энергию T = 0,45 МэВ. Найти энергию фотона до рассеяния.

289. Найти длину волны рентгеновского излучения, если мак­симальная кинетическая энергия комптоновских электронов Т_макс = - 0,19 МэВ.

290. Фотон с энергией Λω = 0,15 МэВ рассеялся на покоив­шемся свободном электроне, в результате чего его длина волны из­менилась на Δλ = 3,0 пм. Найти угол, под которым вылетел компто- новский электрон.

291. Фотон с энергией, в η = 2,0 раза превышающей энергию покоя электрона, испытал лобовое столкновение с покоившимся свободным^ электроном. Найти радиус кривизны траектории элек­трона отдачи в магнитном поле В = 0,12 Т. Предполагается, что электрон отдачи движется перпендикулярно к направлению поля.

292. Фотон, испытав столкновение с релятивистским электро­ном, рассеялся под углом О = 60°, а электрон остановился. Найти комптоновское смещение длины волны рассеянного фотона.

Ч а с τ ь 6

АТОМНАЯ И ЯДЕРНАЯ ФИЗИКА*)

/ 6.1. Рассеяние частиц. Атом Резерфорда—Бора

φ Угол на который рассеивается заряженная частица кулоновским полем неподвижного ядра, определяется формулой:

tg

2 ЬТ^У

Φ ЯгЯг

(6.1а)

где и q₂ — заряды частицы и ядра, 6 —прицельный параметр, Г —кинети­ческая энергия налетающей частицы.

/φ Формула Резерфорда. Относительное число частиц, рассеянных в элементарном телесном угле <iQ под углом θ к первоначальному направ­лению их движения:

fqiq₂\² dQ

^п[ж) ШШ' ^(6Лб)

где л —число ядер фольги на единицу ее поверх­ности, dQ~ sinO¹ d-& d<p.

φ Обобщенная формула Бальмера (рис. 6.1):

те⁴

^ttsaweUf-

Рис. 6.1.

^{1 П} ^ (6.1в)

п%

где ω —частота перехода (рад'с) между энергетическими уровнями с квантовыми числами Πχ и n₂, R — постоянная Ридберга, Ζ — порядковый номер водородо- подобиого иона.

1. Вычислить согласно модели Томсона радиус атома водорода и длину волны испускаемого им света, если известно, что энергия ионизации атома E = 13,6 эВ.

2. Альфа-частица с кинетической энергией 0,27 МэВ рассея­лась золотой фольгой на угол 60°. Найти соответствующее значение прицельного параметра.

3. На какое минимальное расстояние приблизится α-частица с кинетической энергией T = 0,40 МэВ (при лобовом соударении):

а) к покоящемуся тяжелому ядру атома свинца;

б) к первоначально покоившемуся легкому свободному ядру Li⁷?

п J
		tir	\ г
	TV	Серия ,г Пашен а
HW	Серия бальмера Серия и Лайма на

<W N

*) В этой части все формулы даиы в гауссовой системе.

4. Альфа-частица с кинетической энергией T = 0,50 МэВ рассеялась под углом ft = 90° на кулоновском поле неподвижного ядра атома ртути. Найти:

а) наименьший радиус кривизны ее траектории;

б) минимальное расстояние, на которое она сблизилась с ядром.

5. Протон с кинетической энергией T и прицельным пара­метром b рассеялся на кулоновском поле неподвижного ядра атома золота. Найти импульс, переданный данному ядру в результате рассеяния. *

6. Протон с кинетической энергией T = 10 МэВ пролетает на расстоянии Ь = 10 пм от свободного покоившегося электрона. Найти энергию, которую получит электрон, считая, что траектория протона прямолинейная и за время пролета электрон остается прак­тически неподвижным.

7. Частица с кинетической энергией T рассеивается на сфери­ческой потенциальной яме радиуса R и глубины U_0j т. е. полем, в ко­тором потенциальная энергия частицы имеет вид

-ί ° I -U₀

( 0 при г

при г CR₉

где г — расстояние от центра ямы. Найти связь между прицельным параметром частицы b и углом ft, на который она отклонится от пер­воначального направления движения.

8. Неподвижный шар радиуса R облучают параллельным потоком частиц, радиус которых г. Считая столкновение частицы с шаром упругим, найти:

а) угол ft отклонения частицы в зависимости от ее прицельного параметра Ь;

б) относительную долю частиц, которые после столкновения с шаром рассеялись в интервале углов от ft до ft + dft;

в) вероятность того, что частица, испытавшая соударение с ша­ром, рассеется в переднюю полусферу (ft < π/2).

9. Узкий пучок α-частиц с кинетической энергией 1,0 МэВ падает нормально на платиновую фольгу толщины 1,0 мкм. Наблю­дение рассеянных частиц ведется под углом 60° к направлению падающего пучка при помощи счетчика с круглым входным отвер­стием площади 1,0 см², которое расположено на расстоянии 10 см от рассеивающего участка фольги. Какая доля рассеянных α-частиц падает на отверстие счетчика?

10. Узкий пучок α-частиц с кинетической энергией T = = 0,50 МэВ и интенсивностью / = 5,0· IO⁵ част./с падает нормально на золотую фольгу. Найти ее толщину, если на расстоянии г = 15 см от рассеивающего участка под углом ft = 60° к направлению па­дающего пучка плотность потока рассеянных частиц J = = 40 част./(см²-с).

11. Узкий пучок α-частиц падает нормально на серебряную фольгу. За ней установлен счетчик, регистрирующий частицы,

12. рассеянные в соответствии с формулой Резерфорда. При замене серебряной фольги на платиновую той же массовой толщины число регистрируемых в единицу времени α-частиц возросло в η = 1,52 раза. Найти порядковый номер платины, считая, что порядковый номер серебра и массовые числа обоих элементов известны.

13. Узкий пучок α-частиц с кинетической энергией T = = 0,50 МэВ падает нормально на золотую фольгу, массовая толщина которой ρd = 1,5мг/см². Интенсивность пучка I₀ = 5,0· IO⁵ част./с. Найти число α-чаетиц, рассеянных фольгой за τ = 30 мин в интер­валах углов:

а) 59—61°; б) свыше ft₀ = 60° ·

14. Узкий пучок протонов, имеющих скорость ν = 6-IO⁶ м/с, падает нормально на серебряную фольгу толщины d == 1,0 мкм. Найти вероятность рассеяния протонов в заднюю полусферу (ft > > 90°).

15. Узкий пучок α-частиц с кинетической энергией T = — 600 кэВ падает нормально на золотую фольгу, содержащую η = = 1,1-10¹⁹ ядер/см². Найти относительное число α-частиц, рассеи­вающихся под углами ft < Oⁱ₀ = 20°.

16. Узкий пучок протонов с кинетической энергией T = = 1,4 МэВ падает нормально на латунную фольгу, массовая тол- щийа которой pd = 1,5 мг/см². Весовое отношение меди и цинка в фольге равно соответственно 7 : 3. Найти относительное число протонов, рассеивающихся на углы свыше ft₀ = 30°.

17. Найти эффективное сечение ядра атома урана, соответст­вующее рассеянию α-частиц с кинетической энергией T = 1,5 МэВ в интервале углов свыше ft₀ = 60°.

18. Эффективное сечение ядра атома золота, отвечающее рас­сеянию моноэнергетических α-частиц в интервале углов от 90 до 180°, равно Δσ = 0,50 кб. Определить:

а) энергию α-частиц;

б) дифференциальное сечение рассеяния do/d£i (кб/ср), соответ­ствующее углу ft = 60°.

19. Согласно классической электродинамике электрон, дви­жущийся с ускорением w, теряет энергию на излучение по закону

dE 2е² 2

— = w

dt Зсз »

где е — заряд электрона, с — скорость света. Оценить время, за которое энергия электрона, совершающего колебания, близкие к гармоническим с частотой ω = 5-IO¹⁵ рад/с, уменьшится в η = = 10 раз.

20. Воспользовавшись формулой из предыдущей задачи, оце­нить время, в течение которого электрон, движущийся в атоме водорода по круговой орбите радиуса г = 50 пм, упал бы на ядро. Для простоты считать, что вектор w все время направлен к центру атома.

21. Показать, что частота ω фотона, возникающего при пере­ходе электрона между соседними круговыми орбитами водородо- подобного иона, удовлетворяет неравенству ω_η < ω < ω„₊₁, где ω_η и ω_η+1 — частоты обращения электрона вокруг ядра на этих круговых орбитах. Убедиться, что при о частота фотона ω ->■ ω_η.

22. Частица массы т движется по круговой орбите в централь­но-симметричном потенциальном поле U(г) = /ег²/2. Найти с по­мощью боровского условия квантования возможные радиусы ор­бит и уровни энергии этой частицы.

23. Вычислить для атома водорода и иона He⁺:

а) радиус первой боровской орбиты и скорость электрона на ней;

б) кинетическую энергию и энергию связи электрона в основном состоянии;

в) потенциал ионизации, первый потенциал возбуждения и длину волны резонансной линии (n' = η = 1).

24. Вычислить круговую частоту обращения электрона на второй боровской орбите иона He⁺.

25. Найти для водородоподобных систем магнитный момент μ„, соответствующий движению электрона на п-й орбите, а также отношение магнитного момента к механическому μ_η/Μ_η. Вычислить магнитный момент электрона, находящегося на первой боровской орбите.

26. Вычислить индукцию магнитного поля в центре атома водорода, обусловленного движением электрона по первой боров­ской орбите.

27. Рассчитать и изобразить в шкале длин волн спектраль­ные интервалы, в которых заключены серии Лаймана, Бальмера и Пашена для атомарного водорода. Выделить на этой шкале ви­димую область спектра.

28. Какой серии принадлежит спектральная линия атомар­ного водорода, волновое число которой равно разности волновых чисел следующих двух линий серии Бальмера: 486,1 и 410,2 нм? Какова длина волны этой линии?

29. Вычислить для атомарного водорода:

а) длины волн первых трех линий серии Бальмера;

б) минимальную разрешающую способность λ/δλ спектраль­ного прибора, при которой возможно разрешить первые 20 линий серии Бальмера.

30. Излучение атомарного водорода падает нормально на дифракционную решетку ширины I = 6,6 мм. В наблюдаемом спектре под некоторым углом дифракции Φ оказалась на пределе разрешения (по критерию Рэлея) 50-я линия серии Бальмера. Найти этот угол.

31. Какому элементу принадлежит водородоподобный спектр, длины волн линий которого в четыре раза короче, чем у атомарного водорода?

32. Сколько спектральных линий будет испускать атомарный водород, который возбуждают на п-й энергетический уровень?

33. Какие линии содержит спектр поглощения атомарного водорода в диапазоне длин волн от 94,5 до 130,0 нм?

34. Найти квантовое число /г, соответствующее возбужден­ному состоянию иона He⁺, если при переходе в основное состояние этот ион испустил последовательно два фотона с длинами воли 108,5 и 30,4 нм.

35. Вычислить постоянную Ридберга R, если известно, что для ионов He⁺ разность длин воли между головными линиями серий Бальмера и Лаймана Δλ = 133,7 ιιμ.

36. У какого водородоподобного иона разность длин волн между головными линиями серий Бальмера и Лаймана равна 59,3 нм?

37. Найти длину волны головной линии той спектральной серии ионов He⁺, у которой интервал между крайними линиями Δω = 5,18 - IO¹⁵ рад/с.

38. Найти энергию связи электрона в основном состоянии водородоподобных ионов, в спектре которых длина волны третьей линии серии Бальмера равна 108,5 нм.

39. Энергия связи электрона в основном состоянии атома Не равна E₀ — 24,6 эВ. Найти энергию, необходимую для удаления обоих электронов из этого атома.

40. Найти скорость фотоэлектронов, вырываемых электро­магнитным излучением с длиной волны λ = 18,0 нм из ионов He⁺, которые находятся в основном состоянии и покоятся.

41. С какой минимальной кинетической энергией должен двигаться атом водорода, чтобы при неупругом лобовом соударе­нии с другим, покоящимся, атомом водорода один из них оказался Способным испустить фотон? Предполагается, что до соударения оба атома находятся в основном состоянии.

42. Покоившийся атом водорода испустил фотон, соответствую­щий головной лйнии серии Лаймана. Какую скорость приобрел атом?

43. В условиях предыдущей задачи найти, на сколько про­центов энергия испущенного фотона отличается от энергии соответ­ствующего перехода в атоме водорода.

44. Покоящийся ион He⁺ испустил фотон, соответствующий головной линии серии Лаймана. Этот фотон вырвал фотоэлектрон из покоящегося атома водорода, который находился в основном состоянии. Найти скорость фотоэлектрона.

45. Найти скорость возбужденных атомов водорода, если при наблюдении их излучения под углом ft = 45° к направлению движения данных атомов длина волны головной линии серии Лаймана оказалась смещенной на Δλ = 0,20 нм.

46. Согласно постулату Бора — Зоммерфельда при периоди­ческом движении частицы в потенциальном поле должно выполнять­ся следующее правило квантования:

где ρ — импульс частицы, dr — ее элементарное перемещение, η — целые числа. Воспользовавшись этим правилом, найти разре­шенные значения энергии частицы массы т, которая движется:

а) в одномерной прямоугольной потенциальной яме ширины I с бесконечно высокими стенками;

б) по окружности радиуса г;

в) в одномерном потенциальном поле U = α,γ²/2, где а — по­ложительная постоянная;

г) по круговой орбите в центральном поле, где потенциальная энергия частицы U — —α/r, а — положительная постоянная.

47. Найти с учетом движения ядра атома водорода выражения для энергии связи электрона в основном состоянии и для постоян­ной Ридберга. На сколько процентов отличается энергия связи и постоянная Ридберга, полученные без учета движения ядра, от соответствующих уточненных значений этих величин?

48. Найти для атомов легкого и тяжелого водорода (Н и D) разность:

а) энергий связи их электронов в основном состоянии;

б) длин волн головных линий серии Лаймана.

49. Вычислить расстояние между частицами системы в основ­ном состоянии, соответствующую энергию связи и длину волны головной линии серии Лаймана, если системой является:

а) мезоатом водорода, ядром которого служит протон (в мезо­атоме вместо электрона движется мезон, имеющий тот же заряд, но массу в 207 раз большую);

б) позитроний, который состоит из электрона и позитрона, движущихся вокруг общего центра масс.

6.2. Волновые свойства частиц

φ Дебройлевская длина волны частицы с импульсом р:

Ί ^2ПН 1С о ν

λ . (6.2а)

P ^ν

φ Соотношение неопределенностей:

Δ* ■ Ap_x > й. (6.26)

φ Временное и стационарное уравнения Шрёдингера:

(6.2в)

где Ψ —полная волновая функция, ψ— ее координатная часть, Г² —оператор Лапласа, E и U- полная и потенциальная энергии частицы. В сферических координатах:

V= = JLo. 2.д ,_! д / д ] I . *

^ ¹ г dr ^ r2 Sind дЪ V дЪГ г* Sin²A θφ2· ^{(Ь Г)}

X о

dx

- V2т (U-E)

D ^ ехр

где X₁ и X₂- координаты точек, между которыми U>E.

50. Вычислить дебройлевские длины волн электрона, про­тона и атома урана, имеющих одинаковую кинетическую энергию 100 эв.

51. Какую энергию необходимо дополнительно сообщить элек­трону, чтобы его дебройлевская длина волны уменьшилась от 100 до 50 пм?

52. Нейтрон с кинетической энергией T = 25 эВ налетает на покоящийся дейтон (ядро тяжелого водорода). Найти деброй­левские длины волн обеих частиц в системе их центра инерции.

53. Две одинаковые нерелятивистские частицы движутся пер­пендикулярно друг к другу с дебройлевскими длинами волн X₁ и λ₂. Найти дебройлевскую длину волны каждой частицы в системе их центра инерции.

54. Найти дебройлевскую длину волны молекул водорода, соответствующую их наиболее вероятной скорости при комнатной температуре.

55. Вычислить наиболее вероятную дебройлевскую длину волны молекул водорода, находящихся в термодинамическом равно­весии при комнатной температуре.

56. Получить выражение для дебройлевской длины волны λ релятивистской частицы, движущейся с кинетической энергией T. При каких значениях T ошибка в определении λ по нерелятивист­ской формуле не превышает 1% для электрона и протона?

57. При каком значении кинетической энергии дебройлевская длина волны электрона равна его комптоновской длине волны?

58. Найти дебройлевскую длину волны релятивистских элек­тронов, подлетающих к антикатоду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра λ_κ = 10,0 пм?

59. Параллельный поток моноэнергетических электронов па­дает нормально на диафрагму с узкой прямоугольной щелью ши­рины Ь =1,0 мкм. Определить скорость этих электронов, если на экране, отстоящем от щели на расстояние / = 50 см, ширина центрального дифракционного максимума Ax = 0,36 мм.

60. Параллельный поток электронов, ускоренных разностью потенциалов U = 25 В, падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми d = 50 мкм. Опреде­лить расстояние между соседними максимумами дифракционной картины на экране, расположенном на расстоянии / = 100 см от щелей.

61. Коэффициент прозрачности потенциального барьера JJ (х):

    Узкий пучок моноэнергетических электронов падает под углом скольжения ft == 30° на естественную грань монокристалла

62. алюминия. Расстояние между соседними кртеталлическими плоско­стями, параллельными этой грани монокристалла, d = 0,20 нм. При некотором ускоряющем напряжении U₀ наблюдали максимум зеркального отражения. Найти U₀₉ если известно, что следующий максимум зеркального отражения возникал при увеличении уско­ряющего напряжения в η = 2,25 раза.

63. Узкий пучок моноэнергетических электронов падает нор­мально на поверхность монокристалла никеля. В направлении, составляющем угол ft = 55° с нормалью к поверхности, наблюда­ется максимум отражения четвертого порядка при энергии электро­нов T = 180 эВ. Вычислить соответствующее значение межплос­костного расстояния.

64. Узкий пучок электронов с кинетической энергией T = = 10 кэВ проходит через поликристаллическую алюминиевую фоль­гу, образуя на экране систему дифракционных колец. Вычислить межплоскостное расстояние, соответствующее отражению третьего порядка от некоторой системы кристаллических плоскостей, если ему отвечает дифракционное кольцо диаметра D = 3,20 см. Рас­стояние между экраном и фольгой I = 10,0 см.

65. Пучок электронов, ускоренных разностью потенциалов U_y падает на поверхность металла, внутренний потенциал которого U₁ = 15 В. Найти:

а) показатель преломления металла для электронов с U = 150 В;

б) отношение UfU_iy при котором показатель преломления от­личается от единицы не более чем на η = 1,0%.

66. Частица массы т находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна L Найти возможные значения энергии частицы, имея в виду, что реализуются лишь такие состояния ее движения, для которых в пределах данной ямы укладывается целое число деброй- левских полуволн.

67. Интерпретировать квантовые условия Бора на основе волновых представлений: показать, что электрон в атоме водорода может двигаться только по тем круговым орбитам, на которых укладывается целое число дебройлевских волн.

68. Оценить наименьшие ошибки, с которыми можно опре­делить скорость электрона, протона и шарика массы 1 мг, если координаты частиц и центра шарика установлены с неопределен­ностью 1 мкм.

69. Оценить с помощью соотношения неопределенностей не­определенность скорости электрона в атоме водорода, полагая размер атома I= 0,10 нм. Сравнить полученную величину со скоростью электрона на первой боровской орбите данного атома.

70. Показать, что для частицы, неопределенность местополо­жения которой Δ* = λ/2π, где λ — ее дебройлевская длина волны, неопределенность скорости равна по порядку величины самой ско­рости частицы.

71. Свободный электрон первоначально был локализован в области размером / = 0,10 нм. Оценить с помощью соотношения неопределенностей время, за которое ширина соответствующего волнового пакета увеличится в η = 10 раз.

72. Оценить с помощью соотношения неопределенностей мини­мальную кинетическую энергию электрона, локализованного в области размером I = 0,20 нм.

73. Электрон с кинетической энергией T 4 эВ локализо­ван в области размером I = 1 мкм. Оценить с помощью соотношения неопределенностей относительную неопределенность его скорости.

74. Электрон находится в одномерной прямоугольной потен- циальной яме с бесконечно высокими стенками. Ширина ямы равна /. Оценить с помощью соотношения неопределенностей силу дав­ления электрона на стенки этой ямы при минимально возможной его энергии.

75. Частица массы т движется в одномерном потенциаль­ном поле U = £х²/2 (гармонический осциллятор). Оценить с по­мощью соотношения неопределенностей минимально возможную энергию частицы в таком поле.

76. Оценить с помощью соотношения неопределенностей ми­нимально возможную энергию электрона в атоме водорода и соот­ветствующее эффективное расстояние его от ядра.

77. Параллельный пучок атомов водорода со скоростью ν = ™ 600 м/с падает нормально на диафрагму с узкой щелью, за ко­торой на расстоянии I = 1,0 м расположен экран. Оценить с по­мощью соотношения неопределенностей ширину δ щели, при ко­торой ширина изображения ее на экране будет минимальной.

78. Найти частное решение одномерного временного уравнения Шрёдингера для свободно движущейся частицы массы т.

79. Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины / с абсолютно непро­ницаемыми стенками (0 << χ < /). Найти вероятность пребывания частицы в области V₃1 ^ χ ²/₃/.

80. Частица находится в одномерной прямоугольной потен­циальной яме с бесконечно высокими стенками. Ширина ямы равна L Найти нормированные волновые функции стационарных состояний частицы, взяв начало отсчета координаты χ в середи­не ямы.

81. Доказать, что волновые функции стационарных состоя­ний частицы в одномерной потенциальной яме с бесконечно высокими стенками являются ортогональными, т. е. удовлетворяют условию

\ ψ/ζψν dx= 0, если η' Φ п. Здесь / — ширина ямы, η — целые о

числа.

82. Электрон находится в одномерной прямоугольной по­тенциальной яме с бесконечно высокими стенками. Ширина ямы / такова, что энергетические уровни расположены весьма густо.

Найти плотность уровней dN/dE, т. е. их число на единичный интервал энергии, в зависимости от £. Вычислить dN/dE для E = 1,0 эВ, если / == 1,0 см.

83. Частица массы т находится в двумерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Найти:

а) возможные значения энергии частицы, если стороны ямы равны Z₁ и /₂;

б) значения энергии частицы на первых четырех уровнях, если яма квадратная со стороной /.

84. Частица находится в двумерной прямоугольной потен­циальной яме с абсолютно непроницаемыми стенками (0 << χ < < α, 0 <С У <ib). Определить вероятность нахождения частицы с наименьшей энергией в области 0 <ι < а/3.

85. Частица массы т находится в трехмерной кубической по­тенциальной яме с абсолютно непроницаемыми стенками. Сторона куба равна а. Найти:

а) собственные значения энергии частицы;

б) разность энергий 3-го и 4-го уровней;

в) энергию 6-го уровня и соответствующее ему число состояний (кратность вырождения).

86. Показать с помощью уравнения Шрёдингера, что в точке, где потенциальная энергия частицы U(x) имеет конечный разрыв, волновая функция остается гладкой, т. е. ее первая производная по координате непрерывна.

87. Частица массы т находится в одномерном потенциальном поле U(x)_t вид которого показан на рис. 6.2, где U(O) = ос. Найти:

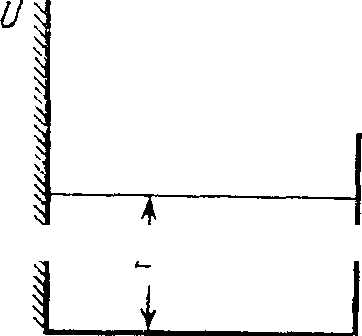
о»

где Iz= уЪпЕЩ. V₀

Показать с помощью графиче­

а) уравнение, определяющее возможные значения энергии частицы в области E < U₀₁ при­вести это уравнение к виду

sin kl = ±kl Yh²/2ml²U

ского решения данного уравне- о ι χ

ния, что возможные значения

энергии частицы образуют дис- Рис. 6.2.

кретный спектр;

б) минимальное значение величины I²U₀, при котором появля­ется первый энергетический уровень в области E < U₀, При каком минимальном значении I²U₀ появляется п-й уровень?

88. Воспользовавшись решением предыдущей задачи, опре­делить вероятность нахождения частицы с энергией E = UJ2 в области л: > /, если I²U₀ = (³A^jt)² №/т.

89. Найти возможные значения энергии частицы массы /и, находящейся в сферически-симметричной потенциальной яме U(г) = = 0 при г < г₀ и U(r) = оо при г — г₀, для случая, когда движение частицы описывается волновой функцией -ф(г), зависящей только от /\

Указание. При решении уравнения Шрёдингера восполь­зоваться подстановкой ψ(>) = x{r)/r.

90. Имея в виду условия предыдущей задачи, найти:

а) нормированные собственные функции частицы в состояниях, где зависит только от г\

б) для основного состояния частицы наиболее вероятное значение /*_вер, а также вероятность нахождения частицы в области г << г_вер.

91. Частица массы т находится в сферически-симметричной потенциальной яме U(г) = 0 при г < г₀ и U(г) = U₀ при г > г₀.

а) Найти с помощью подстановки ψ(/*) = %(r)/r уравнение, определяющее собственные значения энергии E частицы при E << U_0j когда движение описывается волновой функцией if>(/·), зависящей только от г. Привести это уравнение к виду

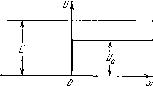
sin kr₀ ■= ± kr₀ Y~ft²/2mrbU₀, где k = У2тЕ/Н.

б) Определить значение величины r₀U_0t при котором появляется первый уровень.

92. Волновая функция частицы массы т для основного со­стояния в одномерном потенциальном поле U(x) = kx²/2 имеет вид = Ae-^aX²_t где А — нормировочный коэффициент, а — положительная постоянная. Найти с помощью уравнения Шрё­дингера постоянную сс и энергию E частицы в этом состоянии.

93. Определить энергию электрона атома водорода в стацио­нарном состоянии, для которого волновая функция = А (1 + + аг)е~^аг, где A_t а и α — некоторые постоянные.

94. Волновая функция электрона в основном состоянии атома водорода имеет вид ψ^) =Ле~~где А —некоторая постоянная, V₁ — первый боровский радиус. Найти:

а) наиболее вероятное расстояние между электроном и ядром;

б) среднее значение модуля кулоновской силы, действующей на электрон;

в) среднее значение потенциальной энергии электрона в поле ядра.

95. Найти средний электростатический потенциал, созда­ваемый электроном в центре атома водорода, если электрон нахо­дится в основном состоянии, для которого волновая функция = = А е*"'/'¹, где А — некоторая по­стоянная, г_г — первый боровский радиус.

6.94. Частицы с массой т и энергией £ движутся слева на потен­циальный барьер (рис. 6. 3). Найти: _Рис, 5.3, а) коэффициент отражения R

этого барьера при E > U_0t

б) эффективную глубину проникновения частиц в область χ > 0 при E < U_0t т. е. расстояние от границы барьера до точки, где плотность вероятности нахождения частицы уменьшается в е раз.

6.95. Воспользовавшись формулой (6.2д), найти для электрона с энергией E вероятность D прохождения потенциального барьера, ширина которого / и высота U_0y если барьер имеет форму, пока­занную:

U (		1¾
	с	5— 1—	V

а) на рис. 6.4;

-I О I Рис. 6.6.

X

б) на рис. 6.5.

		"в
/t
		X

Рис. 6,4.

6.96. Найти с помощью формулы (6.2д) вероятность D про­хождения частицы с массой т и энергией E сквозь потенциальный барьер (рис. 6.6), где U(x) = U₀( 1 — χ²//²).

6.3. Свойства атомов. Спектры

φ Спектральные обозначения термов: ^x(L)_y, где κ = 25+1 — мультиплет- ность, L_y S_i / — квантовые числа,

L = 0, 1, 2, 3, 4, 5, б, ...

(L); S_t P_i D_i F_i G_i H_t I_t ...

φ Термы атомов щелочных металлов:

(6.3а)

2 »

R

T =

(η+ а)

где R — постоянная Ридберга, а —ридберговская поправка, На рис. показана схема термов атома лития, φ Механические моменты атома:

(6.36)

M₁ = h YL (L+1), аналогично M_s и M_j.

φ Правила Хунда:

1. наименьшей энергией обладает терм с максимальным значением S при данной электронной конфигурации и максимально возможным при этом S_MaKC значении L;

2. для основного (нормального) терма J = \L — S|, если подоболочка заполнена менее чем наполовину, и J = L + S в остальных случаях,

0 Распределение Больцмана:

Si

— M^--(E_t-E₁)ZkT

(6.3в)

N,

где gi и g₂ — статистические веса (кратности вырождения) соответствующих уровней,

φ Вероятности переходов атома в единицу времени между уровнем ί и более высоким уровнем 2 —для спонтанного и индуцированного излучения и поглощения:

PII=^aM- P^u^=B_ilU_ta, Я™"=B_liU_uj, (б.Зг)

где A₂It B₂i, B_i2 — коэффициенты Эйнштейна, U_id — спектральная плотность излучения, отвечающая частоте ω перехода между данными уровнями.

E Π г—

-4 -J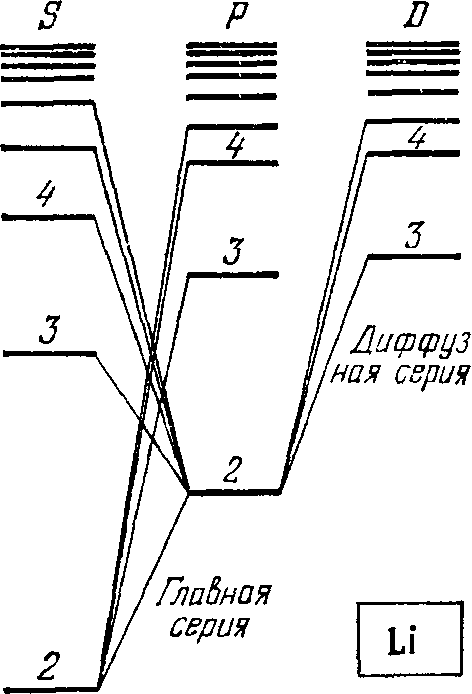

Рис. 6.7.

N

ι ι

S3

^cS

M

Резная серия

К

л

IJMfr ^

L-серия

«а

/Гл/

β

/Г,

К-сери я Рис. 6.8.

φ Связь между коэффициентами Эйнштейна:

Jt²C³

giBn = g2B_n, B₂₁ = -—A_ti. (б.Зд)

φ Схема возникновении рентгеновских спектров (рис. 6.8). φ Закон Мозли для К_а-линий:

где σ —поправка, равная для легких элементов единице.

φ Магнитный момент атома и фактор (множитель) Ланде:

μ = ,/7(7Τ1)μ_β, g=l + ^{J(J+1) +} ^_/+¹⁾-^L(f' ^{+ 1)}· (6.3Ж)

0 Зеемановское расщепление спектральных линий в слабом магнитном поле:

Δω = (/H₁S₁ — т<£₂) μ_βΒ/Η. (б.Зз)

0 При излучении вдоль магнитного поля зеемановские компоненты, обу­словленные переходами mj = т₂, отсутствуют.

6.97. Энергия связи валентного электрона атома лития в состоя­ниях 2S и 2P равна соответственно 5,39 и 3,54 эВ. Вычислить рид- берговские поправки для 5- и Р-термов этого атома.

98. Найти ридберговскую поправку для ЗР-терма атома натрия, первый потенциал возбуждения которого 2,10 В, а энергия связи валентного электрона в основном 35-состояиии 5,14 эВ.

99. Найти энергию связи валентного электрона в основном состоянии атома лития, если известно, что длина волны головной линии резкой серии X₁ = 813 нм и длина волны коротковолновой границы этой серии λ₂ — 350 нм.

100. Определить длины волн спектральных линий, возни­кающих при переходе возбужденных атомов лития из состояния 35 в основное состояние 25. Ридберговские поправки для 5- и P- термов равны —0,41 и —0,04.

101. Длины волн компонент желтого дублета резонансной линии натрия, обусловленной переходом 3P->3S, равны 589.00 и 589,56 нм. Найти величину расщепления ЗР-терма в эВ.

102. Головная линия резкой серии атомарного цезия пред­ставляет собой дублет с длинами волн 1358,8 и 1469,5 нм. Найти интервалы в частотах (рад/с) между компонентами следующих линий этой серии.

103. Выписать спектральные обозначения термов атома водорода, электрон которого находится в состоянии с главным квантовым числом η = 3.

104. Сколько и каких квантовых чисел J может иметь атом в состоянии с квантовыми числами SuL, равными соответственно:

а) 2 и 3; б) 3 и 3; в) 5/2 и 2?

98. Найти возможные значения полных механических мо­ментов атомов, находящихся в состояниях ⁴P и ⁵D.

99. Найти максимально возможный полный механический момент и соответствующее спектральное обозначение терма атома:

а) натрия, валентный электрон которого имеет главное кванто­вое число /г = 4;

б) с электронной конфигурацией ls²2/?3d.

98. Известно, что в F- и D-состояниях - число возможных значений квантового числа J одинаково и равно пяти. Определить спиновый механический момент в этих состояниях.

99. Атом находится в состоянии, мультиплетность которого

равна трем, а полный механическии момент — H V20. Каким может быть соответствующее квантовое число L?

98. Найти возможные мультиплетности κ термов типа:

a) ^yD_2f б) *Рз_/з; в) "F₁.

98. Некоторый атом, кроме заполненных оболочек, имеет три электрона (s, ρ и d) и находится в состоянии с максимально возможным для этой конфигурации полным механическим моментом. Найти в соответствующей векторной модели атома угол между спиновым и полным механическими моментами данного атома.

6.111 Атом находится в состоянии со спиновым квантовым чис­лом S=I, имея полный механический момент й ]/Ί3. В соответ­ствующей векторной модели угол между спиновым и полным механическими моментами # = 73,2°. Написать спектральный символ терма этого состояния.

112. Выписать спектральные символы термов двухэлектронной системы, состоящей из одного р-электрона и одного d-электрона.

113. Система состоит из d-электрона и атома в ²А_/2-состоянии. Найти возможные спектральные термы этой системы.

114. Установить, какие из нижеперечисленных переходов запрещены правилами отбора: ²Dz_fl-^²Pif_i, ⁵P₁-^²Sif₂, ⁵F₃-^³P₂, ⁴Fy_l ⁴D_v,.

6.115 Определить суммарную кратность вырождения ЗО-состоя- ния атома лития. Каков физический смысл этой величины?

116. Найти кратность вырождения состояний ²P₉ ³D и ⁴Z⁷ с максимально возможными значениями полного механического мо­мента.

117. Написать спектральное обозначение терма, кратность вырождения которого равна семи, а квантовые числа LuS связаны соотношением L = 3S.

118. У атома какого элемента заполнены /С-, L- и М-оболоч- ки, 4я-подоболочка и наполовину 4р-подоболочка?

119. Используя правила Хунда, найти основной терм атома, незаполненная подоболочка которого содержит:

а) три р-электрона; б) четыре р-электрона.

116. Найти с помощью правил Хунда полный механический момент атома в основном состоянии, если его незаполненная под­оболочка содержит:

а) три d-электрона; б) семь d-электронов.

116. Воспользовавшись правилами Хунда, найти число элек­тронов в единственной незаполненной подоболочке атома, основной терм которого:

a) ⁵F₂) б) ²Py₂; в) ⁶S_va.

116. Написать с помощью правил Хунда спектральный сим­вол основного терма атома, единственная незаполненная подобо­лочка которого заполнена: ,

а) на 1/3, и S - 1; б) на 70%, и S = 3/2.

116. Единственная незаполненная подоболочка некоторого атома содержит три электрона, причем основной терм атома име­ет L = 3. Найти с помощью правил Хунда спектральный символ основного состояния данного атома.

117. Найти с помощью правил Хунда магнитный момент ос­новного состояния атома, незамкнутая подоболочка которого за­полнена ровно наполовину пятью электронами.

118. Какая относительная часть атомов водорода находится в состоянии с главным квантовым числом п = 2 при температуре

T = 3000 к?

116. Определить отношение числа атомов газообразного на­трия в состоянии 3P к числу атомов в основном состоянии 3S при температуре T = 2400 К. Известно, что переходу 3P ->- 3S соот­ветствует спектральная линия с длиной волны λ = 589 нм.

117. Вычислить среднее время жизни возбужденных атомов, если известно, что интенсивность спектральной линии, обуслов­ленной переходом в основное состояние, убывает в η = 25 раз на расстоянии I = 2,5 мм вдоль пучка атомов, скорость которых ν = 600 м/с.

118. Разреженные пары ртути, атомы который практически все находятся в основном состоянии, осветили резонансной линией ртутной лампы с длиной волны λ = 253,65 нм. При этом мощность испускания данной линии парами ртути оказалась P = 35 мВт. Найти число атомов в состоянии резонансного возбуждения, сред­нее время жизни которого τ = 0,15 мкс.

119. Атомарный литий с концентрацией я = 3,6-IG¹⁶ см"³ находится при температуре T = 1500 К. При этом мощность излу­чения резонансной линии λ = 671 нм (2P->2S) в расчете на еди­ницу объема газа P = 0,30 Вт/см³. Найти среднее время жизни атомов лития в состоянии резонансного возбуждения.

120. Атомарный водород находится в термодинамическом равновесии со своим излучением. Найти:

а) отношение вероятностей индуцированного и спонтанного из­лучений атомов с уровня 2P при температуре T = 3000 К;

б) температуру, при которой эти вероятности станут одинако­выми.

116. Через газ с температурой T проходит пучок света с ча­стотой ω, равной резонансной частоте перехода атомов газа, причем

kT. Показать, учитывая индуцированное излучение, что коэффициент поглощения газа % — κ₀(1 — где κ₀ — коэф­

фициент поглощения при T 0.

116. Длина волны резонансной линии ртути λ = 253,65 нм. Среднее время жизни атоков ртути в состоянии резонансного воз­буждения τ =0,15 мкс. Оценить отношение доплеровского уши- рения этой линии к ее естественной ширине при температуре газа T = 300 К.

117. Найти длину волны iCa-линии меди (Z = 29), если из­вестно, что длина волны TCa-линии железа (Ζ = 26) равна 193 пм.

118. Вычислить с помощью закона Мозли:

а) длину волны /С_а-линии алюминия и кобальта;

б) разность энергий связи К- и L-электронов ванадия.

116. Сколько элементов содержится в ряду между теми, у которых длины волн Ка-лити равны 250 и 179 пм?

117. Найти напряжение на рентгеновской трубке с никеле­вым антикатодом, если разность длин волн Ka-линии и коротко­волновой границы сплошного рентгеновского спектра равна 84 пм.

118. При некотором напряжении на рентгеновской трубке с алюминиевым антикатодом длина волны коротковолновой границы сплошного рентгеновского спектра равна 0,50 нм. Будет ли наблю­даться при этом К-серия характеристического спектра, потенциал возбуждения которой равен 1,56 кВ?

119. При увеличении напряжения на рентгеновской трубке от U_l = 10 кВ до U₂ = 20 кВ интервал длин волн между -ли­нией и коротковолновой границей сплошного рентгеновского спектра увеличился вп = 3,0 раза. Определить порядковый номер элемента антикатода этой трубки.

120. У какого металла в спектре поглощения разность частот

и L-краев поглощения рентгеновских лучей составляет Δω =

- 6,85 . IO¹⁸ рад/с?

116. Вычислить энергию связи К-электрона ванадия, для ко­торого длина волны L-края поглощения X_l = 2,4 нм.

117. Найти энергию связи L-электроиа титана, если разность длин волн головной линии К-серии и ее коротковолновой границы Δλ = 26 пм.

118. Найти кинетическую энергию и скорость фотоэлектро­нов, вырываемых /(_а-излучением цинка с /(-оболочки атомов же­леза, для которого край /(-полосы поглощения λ_κ = 174 пм.

6.КЗ, Вычислить фактор Лайде для атомов:

а) в S-состояниях; б) в синглетных состояниях.

6.144« Вычислить фактор Ланде для следующих термов:

a) "Fu₂; б) Ю_ч· в) ⁵Zy, г) ⁵P₁; д) ³P₀.

145. Вычислить в магнетонах Бора магнитный момент атома:

а) в ^-состоянии;

б) в состоянии ²Г>л_!г\

в) в состоянии с S=I, L = 2 и фактором Ланде g = ⁴/₃.

145. Определить спиновый механический момент атома в со­стоянии D₂, если максимальное значение проекции магнитного момеьта в этом состоянии равно четырем магнетонам Бора.

146. Атом в состоянии с квантовыми числами L = 2, S=I находится в слабом магнитном поле. Найти его магнитный момент, если известно, что наименьший возможный угол между механиче­ским моментом и направлением поля равен 30°.

147. Валентный электрон атома натрия находится в состоянии с главным квантовым числом η — 3, имея при этом максимально возможный полный механический момент. Каков его магнитный момент в этом состоянии?

148. Возбужденный атом имеет электронную конфигурацию Is² 2s² 2ρ 3d и находится при этом в состоянии с максимально возможным полным механическим моментом. Найти магнитный момент атома в этом состоянии.

149. Найти полный механический момент атома в состоянии с S = ³/₂ и L = 2, если известно, что магнитный момент его равен нулю.

150. Некоторый атом находится в состоянии, для которого

S = 2, полный механический момент M = |/"2ft, а магнитный мо­мент равен нулю. Написать спектральный символ соответствующего терма.

145. Атом в состоянии ²Py₂ находится во внешнем магнитном поле с индукцией B = 1,0 кГс. Найти с точки зрения векторной мо­дели угловую скорость прецессии полного механического момента этого атома.

146. Атом в состоянии ²Ptf₂ находится на осп витка радиуса г=5 см с током / = 10 А. Расстояние между атомом и центром витка равно радиусу последнего. Какой может быть максимальная сила, действующая на атом со стороны магнитного поля этого тока?

147. Атом водорода в нормальном состоянии находится на расстоянии г — 2,5 см от длинного прямого проводника с током / = 10 А. Найти силу, действующую на атом.

148. Узкий пучок атомов ванадия в основном состоянии ^Fzj₂ пропускают по методу Штерна и Герлаха через поперечное резко неоднородное магнитное поле протяженностью I₁ = 5,0 см. Расщепление пучка наблюдают на экране, отстоящем от магнита на расстояние I₂ == 15 см. Кинетическая энергия атомов T = 22 мэВ. При каком значении градиента индукции В магнитного поля расстояние между крайними компонентами расщепленного пучка на экране будет составлять δ = 2,0 мм?

149. На сколько подуровней расщепится в слабом магнитном поле терм:

a) ³P₀; б) V_v,; в) 4>._/а?

145. Атом находится в магнитном поле с индукцией B = = 2,50 кГс. Найти полную величину расщепления в электрон- вольтах следующих термов:

a) ¹D; б) *F_r

145. Какой эффект Зеемана (простой, сложный) обнаружи­вают в слабом магнитном поле спектральные линии, обусловленные следующими переходами:

a) ¹P ¹S; б) Ю_Ч2 ²P_v2; в) ^sD₁ ³P₀; г) Ч_ъ *#₄?

145. Определить спектральный символ терма атома, если полная ширина расщепления этого терма в слабом магнитном поле с индукцией В = 3,0 кГс составляет Δ£ = 104 мкэВ.

146. Известно, что спектральная линия λ = 612ΗΜ атома обусловлена переходом между синглетными термами. Вычислить интервал Δλ между крайними компонентами этой линии в магнит­ном поле с индукцией В = 10,0 кГс.

147. Найти минимальное значение индукции В магнитного поля, при котором спектральным прибором с разрешающей спо­собностью λ/δλ = 1,0 · IO⁵ можно разрешить компоненты спектраль­ной линии λ = 536 нм, обусловленной переходом между синглет­ными термами. Наблюдение ведут в направлении, перпендикуляр­ном к магнитному полю.

148. Спектральная линия, обусловленная переходом ³D₁ ->³Р₀, испытывает зеемановское расщепление в слабом магнитном поле. При наблюдении перпендикулярно к направлению магнитного поля интервал между соседними компонентами зеемановской струк­туры линии составляет Δω = 1,32 ■ 10¹⁰ рад/с. Найти индукцию В магнитного поля в месте нахождения источника.

6.163. Длины волн дублета желтой линии натрия (²P ²S) равны 589,59 и 589,00 нм. Найти:

а) отношение интервалов между соседними подуровнями зее- мановского расщепления термов ²Ρη₂ и ²Pι/₂ в слабом магнитном поле;

б) индукцию В магнитного поля, при которой интервал между соседними подуровнями зеемановского расщепления терма ²Py_i

будет в η = 50 раз меньше естественного расщепления терма ²P.

6.164. Изобразить схему возможных пе- ^ реходов в слабом магнитном поле между тер­мами ²Рз/ и ²Stf₂. Вычислить для магнит- ного поля В = 4,5 кГс смещения (в рад/с) зеемановских компонент этой линии.

Рис. 6.9. 6.165. Одну и ту же спектральную ли­

нию, испытывающую аномальный эффект Зеемана, наблюдают в направлении I₉ а также в направлении 2 — после отражения от зеркала (рис. 6.9). Сколько зеемановских компонент будет наблюдаться в обоих направлениях, если спек­тральная линия обусловлена переходом: a) */>.,, ²S ι_/г; б) ³P₂ ³S₁?

6.166. Вычислить полное расщепление Δω спектральной линии ³D₃ ³P₂ в слабом магнитном поле с индукцией B = 3,4 кГс.

6.4. Молекулы и кристаллы

^//Jⁱ///////

-73

φ Вращательная энергия двухатомной молекулы:

E_j=JJ-J (J+ Ib

где /—момент инерции молекулы.

φ Колебательная энергия двухатомной молекулы:

Ε_υ = ηω (v + y₂),

где ω —собственная частота колебаний молекулы.

(б.4а)

(6.46)

φ Средняя энергия квантового гармонического осциллятора при темпера­туре Т:

Ήω

(E)=^ +

(6.4в)

2 ■ _еп' Формула Дебая. Молярная колебательная энергия кристалла:

U — 9RQ

где Θ—дебаевская температура, е/т

19/1

■Π

(6.4г)

(6.4д) (6.4е)

1 _t/TVC x*dx

0 = /to_MaKC/£.

Молярная колебательная теплоемкость кристалла при T <ίθ:

12 / T

T ⁺

θ

φ Распределение свободных электронов в металле вблизи абсолютного нуля:

(6.4ж)

где —концентрация электронов с энергиями E_t E-\-dE. Энергия E отчи­тывается от дна зоны проводимости. φ Уровень Ферми при Т — 0:

(6.4з)

где л— концентрация свободных электронов в металле.

167. Определить угловую скорость вращения молекулы S₂, находящейся на первом возбужденном вращательном уровне, если расстояние между ее ядрами d= 189 пм.

168. Найти для молекулы HCl вращательные квантовые числа двух соседних уровней, разность энергий которых 7,86 мэВ. Рас­стояние между ядрами молекулы 127,5 пм.

169. Найти механический момент молекулы кислорода, вра­щательная энергия которой £ = 2,16 мэВ, а расстояние между ядрами d = 121 пм.

170. Показать, что интервалы частот между соседними спек­тральными линиями чисто вращательного спектра двухатомной молекулы имеют одинаковую величину. Найти момент инерции и расстояние между ядрами молекулы CH, если интервалы между соседними линиями чисто вращательного спектра этих молекул Δω = 5,47 - IO¹² рад/с.

171. Найти для молекулы HF число вращательных уровней, расположенных между нулевым и первым возбужденным коле­бательными уровнями, считая вращательные состояния не завися­щими от колебательных. Собственная частота колебаний этой мо­лекулы равна 7,79 - IO¹⁴ рад/с, расстояние между ядрами — 91,7 пм.

172. Оценить, сколько линий содержит чисто вращательный спектр молекул Br₂, собственная частота колебаний которых ω = = 6,08 · IO¹³ рад/с и момент инерции / = 3,46 * IO"³⁸ г «см².

173. Найти для двухатомной молекулы dN/dE (число враща­тельных уровней на единичный интервал энергии) в зависимости от вращательной энергии Вычислить эту величину для молекулы иода в состоянии с вращательным квантовым числом J= 10. Рас­стояние между ядрами этой молекулы равно 267 пм.

174. 

     

     Найти отношение энергий, которые необходимо затратить для возбуждения двухатомной молекулы на первый колебательный и первый вращательный уровни. Вычислить это отношение для следующих молекул:

Молекула

ω, IO¹⁴ рад/с 8,3 4,35 0,40

d, пм 74 160 267

а) H₂

б) HI

в) I₂

Здесь ω — собственная частота колебаний молекулы, d — рас­стояние между ее ядрами.

167. Собственная частота колебаний молекулы водорода равна 8,25 · IO¹⁴ рад/с, расстояние между ядрами — 74 пм. Найти отно­шение числа этих молекул на первом возбужденном колебательном уровне (и = 1) к числу молекул на первом возбужденном враща­тельном уровне (J — 1) при температуре T = 875 К. Иметь в виду, что кратность вырождения вращательных уровней равна 2J + 1.

168. Вывести формулу (6.4в), используя распределение Больцмана. Получить с помощью нее выражение для молярной колебательной теплоемкости C_vkoji двухатомного газа. Вычислить Cv кол Д^ля газа, состоящего из молекул Cl₂, при температуре 300 К. Собственная частота колебаний этих молекул равна 5,63 · IO¹⁴ рад/с.

169. В середине колебательно-вращательной полосы спектра испускания молекул HCl, где отсутствует «нулевая» линия, запре­щенная правилом отбора, интервал между соседними линиями Δω = 0,79· IO¹³ рад/с. Вычислить расстояние между ядрами мо­лекулы HCl.

170. Вычислить длины волн красного и фиолетового спут­ников, ближайших к несмещенной линии, в колебательном спектре комбинационного рассеяния молекул F₂, если длина волны падаю­щего света λ₀ = 404,7 нм и собственная частота колебаний молекулы ω = 2,15 · IO¹⁴ рад/с.

171. Найти собственную частоту колебаний и коэффициент квазиупругой силы молекулы S₂, если в колебательном спектре комбинационного рассеяния света длины волн красного и фиоле­тового спутников, ближайших к несмещенной линии, равны 346,6 и 330,0 нм.

172. Найти отношение интенсивностей фиолетового и красного спутников, ближайших к несмещенной линии, в колебательном спектре комбинационного рассеяния света на молекулах Cl₂ при температуре T = 300 К, если собственная частота колебаний этих молекул ω = 1,06 · IO¹⁴ рад/с. Во сколько раз изменится это отношение при увеличении температуры вдвое?

173. Рассмотреть возможные типы колебаний следующих ли­нейных молекул:

a) CO₂ (О — С — О); б) C₂H₂ (Н — С — С — Н).

167. Определить число собственных поперечных колебаний струны длины / в интервале частот ω, ω + άω, если скорость рас­пространения колебаний равна v. Считать, что колебания происхо­дят в одной плоскости.

168. Имеется прямоугольная мембрана площадью S. Найти число собственных колебаний, перпендикулярных к ее плоскости, в интервале частот ω, ω + άω, если скорость распространения колебаний равна v.

169. Найти число собственных поперечных колебаний прямо­угольного параллелепипеда объемом V в интервале частот ω, со + άω, если скорость распространения колебаний равна ν.

6.185· Считая, что скорости распространения продольных и поперечных колебаний одинаковы и равны v_y определить дебаев- скую температуру:

а) для одномерного кристалла — цепочки из одинаковых ато­мов, содержащей п₀ атомов на единицу длины;

б) для двумерного кристалла — плоской квадратной решетки из одинаковых атомов, содержащей п₀ атомов на единицу пло­щади;

в) для простой кубической решетки из одинаковых атомов, содержащей п₀ атомов на единицу объема.

186. Вычислить дебаевскую температуру для железа, у ко­торого скорости распространения продольных и поперечных коле­баний равны соответственно 5,85 и 3,23 км/с.

187. Оценить скорость распространения акустических коле­баний в алюминии, дебаевская температура которого Θ = 396 К.

188. Получить выражение, определяющее зависимость тепло­емкости одномерного кристалла — цепочки одинаковых атомов — от температуры T_y если дебаевская температура цепочки равна Θ. Упростить полученное выражение для случая T Θ.

189. Для цепочки одинаковых атомов частота колебаний ω зависит от волнового числа k как ω = о>_макс sin(/az/2), где а>_макс — максимальная частота колебаний, k = 2η/λ — волновое число, соответствующее частоте ω, α — расстояние между соседними ато­мами. Воспользовавшись этим дисперсионным соотношением, найти зависимость от ω числа продольных колебаний, приходящихся на единичный интервал частот, т. е. dN/da>_y если длина цепочки равна /. Зная dN/d&_y найти полное число N возможных продольных колебаний цепочки.

6.ISO. Вычислить энергию нулевых колебаний, приходящую­ся на один грамм меди, дебаевская температура которой Θ = = 330 К.

191. На рис. 6.10 показан график зависимости теплоемкости кристалла от температуры (по Дебаю). Здесь С_кл — классическая теплоемкость, Θ — дебаевская температура. Найти с помощью этого графика:

а) дебаевскую температуру для серебра, если при T = 65 К его молярная теплоемкость равна 15 Дж/(моль · К);

б) молярную теплоемкость алюминия при T = 80 К, если при T = 250 К она равна 22,4 Дж/(моль · К);

в) максимальную частоту колебаний для меди, у которой при T = 125 К теплоемкость отличается от классического значения на 25%.

191. Показать, что молярная теплоемкость кристалла при температуре T Θ, где Θ—дебаевская температура, определя­ется формулой (6.4е).

192. 257

     Можно ли считать температуры 20 и 30 К низкими для железа, теплоемкость которого при этих температурах равна 0,226 и 0,760 Дж/(моль · К)?

9 И. Е. Иродов

6.194. Вычислить среднее значение энергии нулевых колебаний, приходящейся на один осциллятор кристалла в модели Дебая, если дебаевская температура кристалла равна Θ.

Рис. 6.10.

195. Изобразить спектр распределения энергии колебаний кристалла по частотам (без учета нулевых колебаний). Рассмотреть два случая: T = Θ/2 и T = θ/4, где Θ —дебаевская темпера­тура.

196. Оценить максимальные значения энергии и импульса фонона (звукового кванта) в меди, дебаевская температура которой равна 330 К.

197. Воспользовавшись формулой (6.4ж), найти при T= 0:

а) максимальную кинетическую энергию свободных электронов в металле, если их концентрация равна п;

б) среднюю кинетическую энергию свободных электронов, если известна их максимальная кинетическая энергия Т_макс.

195. Сколько процентов свободных электронов в металле при T = O имеет кинетическую энергию, превышающую половину максимальной?

196. Найти число свободных электронов, приходящихся на один атом натрия при T = 0, если уровень Ферми E_f = 3,07 эВ и плотность натрия равна 0,97 г/см³.

197. До какой температуры надо было бы нагреть класси­ческий электронный газ, чтобы средняя энергия его электронов оказалась равной средней энергии свободных электронов в меди при Т=0? Считать, что на каждый атом меди приходится один свободный электрон.

' 6.201. Вычислить интервал (в электронвольтах) между сосед­ними уровнями свободных электронов в металле при T = 0 вблизи уровня Ферми, если концентрация свободных электронов η = = 2,0 · IO²² см~³ и объем металла V = 1,0 см³.

202. Воспользовавшись формулой (6.4ж), найти при T = 0:

а) распределение свободных электронов по скоростям;

б) отношение средней скорости свободных электронов к их максимальной скорости.

202. Исходя из формулы (6.4ж), найти функцию распреде­ления свободных электронов в металле при T = 0 по дебройлев- ским длинам волн.

203. Вычислить давление электронного газа в металлическом натрии при T= 0, если концентрация свободных электронов в нем η = 2,5 · IO²² см^-3. Воспользоваться уравнением для давления идеального газа.

204. Повышение температуры катода в электронной лампе от значения T = 2000 К на AT = 1,0 К увеличивает ток насыщения на η — 1,4%. Найти работу выхода электрона из материала ка­тода.

205. Найти коэффициент преломления металлического натрия для электронов с кинетической энергией T = 135 эВ. Считать, что на каждый атом натрия приходится один свободный электрон.

206. Найти минимальную энергию образования пары элект­рон — дырка в чистом беспримесном полупроводнике, электро­проводность которого возра­стает в η = 5,0 раз при уве­личении температуры от T₁ = 300 К до T₂ = 400 к.

207. При очень низких температурах красная грани­ца фотопроводимости чистого беспримесного германия λ_κ = = 1,7 мкм. Найти темпера­турный коэффициент сопро­тивления данного германия при комнатной температуре.

208. На рис 6.11 показан график зависимости логариф­ма электропроводности от обратной температуры (T_t кК) дл я некоторого полуп ровод- ника п-типа. Найти с помощью

Рис. 6.1 и

этого графика ширину запрещенной зоны полупроводника и энер­гию активации донорных уровней.

202. 9*

     Удельное сопротивление некоторого чистого беспримес­ного полупроводника при комнатной температуре ρ = 50 Ом-см. После включения источника света оно стало р_А = 40 Ом-см, а через t = 8 мс после выключения источника света удельное сопро-

259

,тавление оказалось р₂ — 45 Ом-см. Найти среднее время жизни электронов проводимости и дырок.

202. При измерении эффекта Холла пластинку из полупро­водника р-типа ширины /г = 10 мм и длины / = 50 мм поместили в магнитное поле с индукцией В — 5,0 кГс. К концам пластинки приложили разность потенциалов U = 10 В. При этом холлов- ская разность потенциалов оказалась V_h — 50 мВ и удельное сопротивление ρ = 2,5 Ом-см. Найти концентрацию дырок и их подвижность.

203. При измерении эффекта Холла в магнитном поле с ин­дукцией В = 5,0 кГс поперечная напряженность электрического поля в чистом беспримесном германии оказалась в η = 10 раз меньше продольной напряженности электрического поля. Найти разность подвижностей электронов проводимости и дырок в данном полупроводнике.

204. В некотором полупроводнике, у которого подвижность электронов проводимости в η = 2,0 раза больше подвижности дырок, эффект Холла не наблюдался. Найти отношение концентра­ций дырок и электронов проводимости в этом полупроводнике.

6.5. Радиоактивность

φ Основной закон радиоактивного распада:

N = N_Qe-M. (6.5а)

φ Связь между постоянной распада λ, средним временем жизни τ и период дом полураспада Т:

^λ=Τ = ^r- <⁶·⁵⁶)

Q Удельная активность —это активность единицы массы вещества.

202. Зная постоянную распада λ ядра, определить:

а) вероятность того, что оно распадется за промежуток вре­мени, от 0 до t;

б) его среднее время жизни τ.

202. Какая доля радиоактивных ядер кобальта, период полу­распада которых 71,3 дня, распадется за месяц?

203. Сколько β-частиц испускает в течение одного часа 1,0 мкг изотопа Na²⁴, период полураспада которого равен 15 ч?

204. При изучении β-распада радиоизотопа Mg²³ в момент t = 0 был включен счетчик. К моменту t_x = 2,0 с он зарегистрировал N₁ β-частиц, а к моменту I₂ = St₁ — в 2,66 раза больше. Найти среднее время жизни данных ядер.

vj 6.218: Активность некоторого препарата уменьшается в 2,5 раза за 7,0 суток. Найти его период полураспада.

6.219. В начальный момент активность некоторого радиоизотопа составляла 650 част./мин. Какова будет активность этого препа­рата по истечении половины его периода полураспада?

220. Найти постоянную распада и среднее время жизни радио­активного изотопа Со⁵⁵, если известно, что его активность умень­шается на 4,0% за час? Продукт распада нерадиоактивен.

221. Препарат U²³⁸ массы 1,0 г излучает 1,24· IO⁴ α-частиц в секунду. Найти период полураспада этого изотопа и активность препарата.

222. Определить возраст древних деревянных предметов, если известно, что удельная активность изотопа С¹⁴ у них составляет 3/5 удельной активности этого изотопа в только что срубленных деревьях. Период полураспада ядер С¹⁴ равен 5570 лет.

223. В урановой руде отношение числа ядер U²³⁸ к числу ядер Pb²⁰⁶ η = 2,8. Оценить возраст руды, считая, что весь свинец Pb²⁰⁶ является конечным продуктом распада уранового ряда. Период полураспада ядер U²³⁸ равен 4,5 · IO⁹ лет.

224. Вычислить удельные активности изотопов Na²⁴ и U²³⁵, пе­риоды полураспада которых равны соответственно 15 ч и 7,1 · IO⁸ лет.

225. В кровь человека ввели небольшое количество раствора, содержащего радиоизотоп Na²⁴ активностью А = 2,0* IO³ расп./с. Активность 1 см³ крови, взятой через t = 5,0 ч, оказалась A^r = = 16 расп./(мин-см³). Период полураспада данного радиоизотопа T = 15 ч. Найти объем крови человека.

226. Удельная активность препарата, состоящего из актив­ного кобальта Со⁵⁸ и неактивного Со⁵⁹, составляет 2,2 · IO¹² расп./(с · г). Период полураспада Со⁵⁸ равен 71,3 суток. Найти отношение массы активного кобальта в этом препарате к массе препарата (в %).

227. Некоторый препарат содержит две β-активные компонен­ты с различными периодами полураспада. Измерения дали следуй- щую зависимость натурального логарифма активности препарата от времени t в часах:

t o 1 2 3 5 7 10 14 20

In Л iio 3,60 3,10 2,60 2,06 1,82 1,60 1,32 .0,90

Найти периоды полураспада обеих компонент и отношение чисел радиоактивных ядер этих компонент в момент t = 0.

220. Радиоизотоп P³², период полураспада которого T = = 14,3 сут, образуется в ядерном реакторе с постоянной скоростью q = 2,7-10⁹ ядер/с. Через сколько времени после начала обра­зования этого радиоизотопа его активность станет А = 1,0 χ X IO⁹ расп./с?

221. Радиоизотоп A₁ с постоянной распада X₁ превращается в радиоизотоп A₂ с постоянной распада λ₂. Считая, что в начальный момент препарат содержал только ядра изотопа A₁, найти:

а) закон накопления радиоизотопа A₂ со временем;

б) промежуток времени, через который активность радиоизо­топа A₂ достигнет максимума.

220. Решить предыдущую задачу, если X₁ = X₂ = λ.

221. Радиоизотоп A₁ испытывает превращения по цепочке Ai -+· A₂-+ Аз (стабилен) с соответствующими постоянными рас- вада λχ и λ₂. Считая, что в начальный момент препарат содержал только ядра изотопа A_i в количестве N_10f найти закон накопления стабильного изотопа A₃.

222. Радиоактивный изотоп Bi²¹⁰ распадается по цепочке

Bi²¹⁰_irPo^2l0-^Pb²⁰⁶ (стабилен),

где постоянные распада K₁ — 1,60· IO^re с"¹, λ₂ = 5,80· IO^-sC"¹. Вы­числить а- и β-активности препарата Bi²¹⁰ массы 1,00 мг через месяц после его изготовления.

220. а) Какой изотоп образуется из α-активного Ra²²⁶ в ре­зультате пяти α-распадов и четырех β'-распадов?

б) Сколько а- и β-'распадов испытывает U²³⁸, превращаясь в конечном счете в стабильный изотоп Pb²⁰⁶?

220. Покоившееся ядро Po²⁰⁰ испустило α-частицу с кинети­ческой энергией T_a = 5,77 МэВ. Найти скорость отдачи дочернего ядра. Какую долю полной энергии, освобождаемой в этом процессе, составляет энергия отдачи дочернего ядра?

221. Определить количество тепла, которое выделяет 1,00 мг препарата Po²¹⁰ за период, равный среднему времени жизни этих ядер, если известно, что испускаемые α-частицы имеют кинетиче­скую энергию 5,3 МэВ и практически все дочерние ядра образуются непосредственно в основном состоянии.

222. Альфа-распад ядер Po²¹⁰ (из основного состояния) сопро­вождается испусканием двух групп α-частиц с кинетическими энергиями 5,30 и 4,50 МэВ. В результате испускания этих частиц дочерние ядра оказываются соответственно в основном и возбужден­ном состояниях. Найти энергию γ-квантов, испускаемых возбужден­ными ядрами.

223. Средний пробег α-частицы в воздухе при нормальных условиях определяется следующей формулой R = 0,98· IO"²⁷ vl см, где v₀ (см/с) — начальная скорость α-частицы. Воспользовавшись этой формулой, найти для α-частицы с начальной кинетической энергией 7,0 МэВ:

а) ее средний пробег;

б) среднее число пар ионов, которые образует данная α-частица на всем пути R_y а также на первой половине его, считая, что энергия образования одной пары ионов равна 34 эВ.

220. Найти энергию Q, выделяющуюся при β"- и β⁺-ρ3αιадах и при К-захвате, если известны массы материнского атома M_u9 дочернего атома М_д и электрона т.

221. Найти с помощью табличных значений масс атомов максимальную кинетическую энергию β-частиц, испускаемых яд­рами Be¹⁰, и соответствующую кинетическую энергию отдачи до­черних ядер, которые образуются непосредственно в основном со­стоянии.

222. Оценить количество тепла, выделенного за сутки в кало­риметре β"-3ΚΤΗΒΗΒΐΜ препаратом Na²⁴, масса которого т 1,0 мг.

Считать, что β-частицы в среднем имеют кинетическую энергию, ДО равную V₃ максимально возможной при данном распаде. Период полураспада Na²⁴ T = 15 ч.

220. Вычислить с помощью табличных значений масс атомов кинетические энергии позитрона и нейтрино, испускаемых ядром С¹¹ в случае, если дочернее ядро не испытывает отдачи.

221. Найти кинетическую энергию ядра отдачи при позитрон- ном распаде ядра N¹³ в том случае, когда энергия позитрона макси­мальна.

222. Определить с помощью табличных значений масс атомов скорость ядра, возникающего в результате /(-захвата в атоме Be⁷, если дочернее ядро оказывается непосредственно в основном состоянии.

223. Возбужденные ядра Ag¹⁰⁹, переходя в основное состояние, испускают или γ-кванты с энергией 87 кэВ, или конверсионные /(-электроны (их энергия связи 26 кэВ). Определить скорость этих электронов.

224. Свободное покоившееся ядро Ir¹⁹¹ с энергией возбуждения E = 129 кэВ перешло в основное состояние, испустив γ-квант. Вычислить относительное изменение энергии γ-кванта, возникающее в результате отдачи ядра.

225. С какой относительной скоростью должны сближаться источник и поглотитель, состоящие из свободных ядер Ir¹⁹¹, чтобы наблюдалось максимальное поглощение γ-квантов с энергией ε = = 129 кэВ?

226. Источник γ-квантов расположен на h = 20 м выше по­глотителя. С какой скоростью необходимо перемещать вверх ис­точник, чтобы в месте расположения поглотителя полностью ском­пенсировать гравитационное изменение энергии γ-квантов, обуслов­ленное полем тяготения Земли?

227. На какую минимальную высоту необходимо поднять источник γ-квантов, содержащий возбужденные ядра Zn⁶⁷, чтобы при регистрации на поверхности Земли гравитационное смещение линии Мёссбауэра превзошло ширину этой линии? Известно, что регистрируемые γ-кванты имеют энергию ε = 93 кэВ и возникают при переходе ядер Zn⁶⁷ в основное состояние, а среднее время жизни возбужденного состояния τ = 14 мкс.

6.6. Ядерные реакции

φ Энергия связи ядра:

E_cb = Zm_n + (A-Z) Ht_n-M_i (6.6а)

где Ζ—заряд ядра (в единицах е), Л —массовое число, т_н, т_п и M -—массы атома водорода, нейтрона и атома_л соответствующего данному ядру.

Для расчетов удобнее пользоваться формулой:

^CB = ^ΖΔΗ + (Л - Ζ) Δ„ - Δ, (6.66)

где Δ_Η, Δ_η и Δ —избыток массы атома водорода, нейтрона и атома, соответ­ствующего данному ядру.

φ Энергетическая схема ядерной реакции

т + m' + M'+Q (б.бв)

показана на рис. 6.12, где т + М и m' + ΛΓ·— суммы масс покоя частиц до и

~ -ν

после реакции, T и T' — суммарные кинетические энергии частиц до и после реакции (в системе центра инерции), Е* — энергия возбуждения промежуточ- j ного ядра, Q —энергия реакции, E и E^f —

энергии связи частиц т и т^г в промежу­точном ядре, 1> 2у 3 — уровни энергии про­межуточного ядра.

φ Пороговая (минимальная) кинетиче­ская энергия налетающей частицы, при ко­торой становится возможной эндоэнергетиче- ская ядерная реакция:

Q

пор

M

Рис 6.12.

_ m + Λί

(б.бг)

где т и М — массы налетающей частицы и ядра мишени.

220. Альфа-частица с кинетической энергией T_a = 7,0 Мэв упруго рассеялась на первоначально покоившемся ядре Li⁶. Опре­делить кинетическую энергию ядра отдачи, если угол между направ­лениями разлета обеих частиц Θ — 60°.

221. Нейтрон испытал упругое соударение с первоначально покоившимся дейтоном. Определить долю кинетической энергии, теряемую нейтроном:

а) при лобовом соударении;

б) при рассеянии под прямым углом.

220. Определить значение максимально возможного угла, на который рассеивается дейтон при упругом соударении с перво­начально, покоившимся протоном.

221. Считая радиус ядра равным R = 0,13]/Л~ пм, где А — его массовое число, оценить плотность ядер, а также число нукло­нов, в единице объема ядра.

222. Написать недостающие обозначения (χ) в следующих ядерных реакциях:

а) В¹⁰ (х₉ а) Be⁸;

б) О¹⁷ (d, п) х;

в) Na²³ (р₉ х) Ne²⁰;

г) х(р, п) Ar³⁷.

220. Показать, что энергия связи ядра с массовым числом А и зарядом Z может быть определена по формуле (6.66).

221. Найти энергию связи ядра, которое имеет одинаковое число протонов и нейтронов и радиус, в полтора раза меньший

радиуса ядра Al²⁷.

220. Найти с помощью табличных значений масс атомов:

а) среднюю энергию связи на один нуклон в ядре О¹⁶;

)	I )		yZ	i	I
	/
1	f				T
Oltll '		\	1 . >	\
				Q
				' \	f
	ε		Eit >	' т'*н' E'
	\	,1	f \	f

м*

б) энергию связи нейтрона и α-частицы в ядре B¹*;

в) энергию, необходимую для разделения ядра О¹⁶ на четыре одинаковые частицы.

220. Найти разность энергий связи нейтрона и протона в ядре В¹¹. Объяснить причину их различия.

221. Вычислить энергию, необходимую для разделения ядра, Ne²⁰ на две α-частицы и ядро С¹², если известно, что энергии связи на один нуклон в ядрах Ne²⁰, He⁴ и С¹² равны соответственно 8,03, 7,07 и 7,68 МэВ.

222. Вычислить в а. е. м. массу:

а) атома Li⁸, энергия связи ядра которого 41,3 МэВ;

б) ядра С¹⁰, у которого энергия связи на один нуклон равна 6,04 МэВ.

220. Известны энергии связи E_l9 E₂, E₂ и E_i ядер, участвую­щих в ядерной реакции A₁ + A₂-+ A₃ + Л₄. Найти энергию этой реакции.

221. Считая, что в одном акте деления ядра U²³⁵ освобожда­ется энергия 200 МэВ, определить:

а) энергию, выделяющуюся при сгорании одного килограмма изотопа U²³⁵, и массу каменного угля с теплотворной способностью 30 кДж/г, эквивалентную в тепловом отношении одному килограмму U²³⁵;

б) массу изотопа U²³⁵, подвергшегося делению при взрыве атом­ной бомбы с тротиловым эквивалентом 30 килотонн, если тепловой эквивалент тротила равен 4,1 кДж/г.

220. Сколько тепла выделяется при образовании одного грамма He⁴ из дейтерия H²? Какая масса каменного угля с теплотворной спо­собностью 30 кДж/г эквивалентна в тепловом отношении полученной величине?

221. Вычислить с помощью табличных значений масс атомов энергию на один нуклон, которая выделяется при протекании- термоядерной реакции Li⁶ + H² 2Не⁴. Сравнить полученную величину с энергией на один нуклон, освобождающейся при делении ядра U²³⁵.

222. Определить энергию реакции Li⁷ + ρ 2Не⁴, если -из­вестно, что энергии связи на один нуклон в ядрах Li⁷ и He⁴ равны соответственно 5,60 и 7,06 МэВ.

223. Найти энергию реакции N¹⁴ (а, р) О¹⁷, если кинетичес­кая энергия налетающей α-частицы T_a = 4,0 МэВ и протон, выле­тевший под углом # = 60° к направлению движения α-частицы, имеет кинетическую энергию T_p = 2,09 МэВ.

224. Определить с помощью табличных значений масс атомов энергию следующих реакций:

а) Li⁷(/?, п) Be⁷;

б) Be⁹ (я, γ) Be¹⁰;

в) Li⁷ (а, п) В¹⁰;

г) О¹⁶ (d, а) N¹⁴.

220. ; Найти с помощью табличных значений масс атомов скорости продуктов реакции Β¹⁰(η,α) Li⁷, протекающей B₁ резуль­тат

тате взаимодействия весьма медленных нейтронов с покоящимися ядрами бора.

220. Протоны, налетающие на неподвижную литиевую мишень, возбуждают реакцию Li⁷ (ρ, я) Be⁷. При каком значении кинети­ческой энергии протона возникший нейтрон может оказаться поко­ящимся?

221. Альфа-частица с кинетической энергией T = 5,3 МэВ возбуждает ядерную реакцию Ве⁹(а, я) С¹², энергия которой Q = = +5,7 МэВ. Найти кинетическую энергию нейтрона, вылетев­шего под прямым углом к направлению движения α-частицы.

222. Протоны с кинетической энергией T = 1,0 МэВ бомбар­дируют литиевую мишень, в результате чего наблюдается ядерная реакция ρ + Li⁷ -»■ 2Не⁴. Найти кинетическую энергию каждой α-частицы и угол между направлениями их разлета, если разлет происходит симметрично по отношению к направлению налетаю­щих протонов.

223. Частица массы т налетает на покоящееся ядро массы Λί, возбуждая эндоэнергетическую реакцию. Показать, что пороговая (минимальная) кинетическая энергия, при которой эта реакция становится возможной, определяется формулой (б.бг).

224. Какую кинетическую энергию необходимо сообщить про­тону, чтобы он смог расщепить покоящееся ядро тяжелого водо­рода H², энергия связи которого E_cb = 2,2 МэВ?

225. При облучении моноэнергетическим пучком протонов мишеней из лития и бериллия было обнаружено, что реакция Li⁷(p, я) Be⁷ — 1,65 МэВ идет, a Be⁹ (/?, я) B⁹ — 1,85 МэВ не идет. Найти возможные значения кинетической энергии протонов.

226. Для возбуждения реакции (я, а) на покоящихся ядрах В¹¹ пороговая кинетическая энергия нейтронов T¹_nop = 4,0 МэВ. Найти энергию этой реакции.

227. Вычислить пороговые кинетические энергии протонов для возбуждения реакций (/?, я) и (р, d) на ядрах Li⁷.

228. Найти с помощью табличных значений масс атомов по­роговую кинетическую энергию α-частицы для ядерной реакции Li⁷(a, я) В¹⁰. Какова при этом скорость ядра В¹⁰?

229. Нейтрон с кинетической энергией T = 10 МэВ возбуж­дает ядерную реакцию С¹²(/г, a) Be⁹, порог которой T_nop = 6,17 МэВ. Найти кинетическую энергию α-частиц, вылетающих под прямым углом к падающим нейтронам.

230. На сколько процентов пороговая энергия γ-кванта пре­восходит энергию связи дейтона (Е_св = 2,2 МэВ) в реакции у + H² я + р?

231. Протон с кинетической энергией T= 1,5 МэВ захва­тывается ядром H². Найти энергию возбуждения образовавшегося ядра.

232. Выход ядерной реакции С¹³ (d, я) N¹⁴ имеет максимумы при следующих значениях кинетической энергии T_i налетающих дейтонов: 0,60, 0,90, 1,55 и 1,80 МэВ. Найти с помощью табличных значений масс атомов соответствующие энергетические уровни про­межуточного ядра, через которые идет эта реакция.

233. Узкий пучок тепловых нейтронов ослабляется в η — 360 раз после прохождения кадмиевой пластинки, толщина которой d = 0,50 мм. Определить эффективное сечение взаимодействия этих нейтронов с ядрами кадмия.

234. Определить, во сколько раз уменьшится интенсивность узкого пучка тепловых нейтронов после прохождения слоя тяже­лой воды толщиной d = 5,0 см. Эффективные сечения взаимодейст­вия ядер дейтерия и кислорода для тепловых нейтронов равны я соответственно O₁ — 7,0 б и σ₂ — 4,2 б.

235. Узкий пучок тепловых нейтронов проходит через пла­стинку из железа, для которого эффективные сечения поглощения и рассеяния равны соответственно о_а = 2,5 б,O_s= Π б· Определить относительную долю нейтронов, выбывших из пучка в результате рассеяния, если толщина пластинки d = 0,50 см.

236. Выход ядерной реакции с образованием радиоактивных изотопов можно характеризовать двояко: либо отношением w числа ядерных реакций к числу бомбардирующих частиц, либо величиной k — отношением активности возникшего радиоизотопа к числу бомбардировавших частиц. Найти:

а) период полураспада образующегося радиоизотопа, считая, что w и k известны;

б) выход w реакции Li⁷ (р, п) Be⁷, если после облучения литие­вой мишени пучком протонов (в течение t = 2,0 ч при токе в пучке /= ЮмкА) активность изотопа Be⁷ оказалась А = 1,35· IO⁸ расп./с, а его период полураспада 7 — 53 сут.

220. Тонкую золотую фольгу, состоящую из стабильного изо­топа Au¹⁹⁷, облучают по нормали к поверхности тепловыми нейтро­нами, плотность потока которых J = 1,0· IO¹⁰ част ./(с-см²). Масса фольги т = 10 мг. В результате захвата нейтронов возникает β-активный изотоп Au¹⁹⁸, эффективное сечение образования кото­рого σ — 98 б и период полураспада T = 2,7 сут. Найти:

а) время облучения, за которое число ядер Au¹⁹⁷ уменьшится на η = 1,0%;

б) максимальное число ядер Au¹⁹⁸, которое может образоваться в процессе длительного облучения.

220. Тонкую фольгу из некоторого стабильного изотопа об­лучают тепловыми нейтронами, падающими по нормали к ее поверх­ности. В результате захвата нейтронов возникает радиоактивный изотоп с постоянной распада λ. Найти закон накопления этого радиоизотопа N(t) в расчете на единицу поверхности фольги. Плот­ность потока нейтронов равна J_t число ядер на единицу поверх­ности фольги η и эффективное сечение образования активных ядер о.

221. Золотую фольгу массы т = 0,20 г облучали в течение 1 — 6,0 ч потоком тепловых нейтронов, падающим по нормали к ее поверхности. Через τ = 12 ч после окончания облучения ак­тивность фольги оказалась А = 1,9· IO⁷ расп./с. Найти плотность потока нейтронов, если эффективное сечение образования ядра радиоактивного изотопа σ = 96 б, а его период полураспада T = = 2,7 сут.

222. Сколько нейтронов будет в сотом поколении, если про­цесс деления начинается с /V₀ = 1000 нейтронов и происходит в среде с коэффициентом размножения к = 1,05?

223. Найти число нейтронов, возникающих в единицу времени в урановом реакторе, тепловая мощность которого P = 100 МВт, если среднее число нейтронов на каждый акт деления ν = 2,5. Считать, что при каждом делении освобождается энергия E = = 200 МэВ.

224. В ядерном реакторе на тепловых нейтронах среднее время жизни одного поколения нейтронов τ = 0,10 с. Считая коэф­фициент размножения к = 1,010, найти:

а) во сколько раз увеличится количество нейтронов в реакторе, а следовательно и его мощность, за время ί = 1,0 мин;

б) период реактора T, т. е. время, за которое его мощность увеличится в е раз.

6.7. Элементарные частицы

φ Выражения для полной энергии и импульса релятивистской частицы:

Е — т^ + Т, рс = Ут {Т + 2(TIqC²)₉ (6.7а)

где Г —кинетическая энергия частицы.

® При рассмотрении столкновения частиц полезно использовать инвариант­ную величину;

Е* — р*-с* = т*с*., (6.7 б)

где E и р — полная энергия и импульс системы до столкновения, m_Q—масса покоя образовавшейся частицы.

φ Пороговая (минимальная) кинетическая энергия частицы т, налетающей на покоящуюся частицу M_i для возбуждения эндоэнгргетической реакции т+М /¾-+/?½ + ... :

пор 2М ' '

где m, M_t пц₉ т₂, ... — массы покоя соответствующих частиц. φ Квантовые числа, приписываемые элементарным частицам: Q —электрический заряд, L — лептониый заряд, В — барионный заряд,

Г —изотопический спин, 7^ —его проекция, S—странность, S~2 (Q)-B_t К —гиперзаряд, +

φ Связь между квантовыми числами сильно взаимодействующих частиц:

¢=^+-2-=^+-¾^- <⁶-.^7г>

φ При взаимодействии частиц выполняются законы сохранения Q, L и В зарядов. В сильных взаимодействиях выполняются также законы сохранения 5 (или К), T и его проекции T_z.

220. Вычислить кинетические энергии протонов, импульсы которых равны 0,10, 1,0 и 10 ГэВ/с, где с — скорость света.

221. Найти средний путь, проходимый π-мезонами с кине­тической энергией, которая в η = 1,2 раза превышает их энергию покоя. Среднее время жизни очень медленных π-мезонов τ₀ = 25,5 не.

222. Отрицательные л>мезоны с кинетической энергией T = = 100 МэВ пролетают от места рождения до распада в среднем рас­стояние / = И м. Найти собственное время жизни этих мезонов.

223. Имеется узкий пучок π'-мезонов с кинетической энергией T₉ равной энергии покоя данных частиц. Найти отношение потоков частиц в сечениях пучка, отстоящих друг от друга на / — 20 м. Собственное среднее время жизни этих мезонов τ₀ = 25,5 не.

224. Остановившийся я⁺-мезон распался на мюон и нейтрино. Найти кинетическую энергию мюона и энергию нейтрино.

225. Найти кинетическую энергию нейтрона, возникшего при распаде остановившегося 2~-гиперона η + π").

226. Остановившийся положительный мюон распался на по­зитрон и два нейтрино. Найти максимально возможную кинети­ческую энергию позитрона.

227. Покоившаяся нейтральная частица распалась на про­тон с кинетической энергией T = 5,3 Мэв и π'-мезон. Найти массу этой частицы. Как она называется?

228. Отрицательный π-мезон с кинетической энергией T = = 50 МэВ распался на лету на мюон и нейтрино. Найти энергию нейтрино, вылетевшего под прямым углом к направлению движе­ния π-мезона.

229. 2⁺-гиперон с кинетической энергией T^t₂ = 320 МэВ рас­пался на лету на нейтральную частицу и я⁺-мезон, который вылетел с кинетической энергией T_n = 42 МэВ под прямым углом к направ­лению движения гиперона. Найти массу покоя нейтральной части­цы (в МэВ).

230. Нейтральный π-мезон распался на лету на два γ-кванта с одинаковой энергией. Угол между направлениями разлета γ-квантов θ == 60°. Найти кинетическую энергию π-мезона и энергию каждого γ-кванта.

231. Релятивистская частица с массой покоя т в результате столкновения с покоившейся частицей массы M возбуждает реак­цию рождения новых частиц: т + M т_г + т₂ + где справа записаны массы покоя возникших частиц. Воспользовавшись инвариантностью величины E² — р²с², показать, что пороговая ки­нетическая энергия частицы т для этой реакции определяется формулой (6.7в).

232. Позитрон с кинетической энергией T = 750 кэВ нале­тает на покоящийся свободный электрон. В результате анниги-

ляции возникают два γ-кванта с одинаковыми энергиями. Опреде­лить угол между направлениями их разлета.

220. Найти пороговую энергию γ-кванта, необходимую для образования:

а) пары электрон — позитрон в поле покоящегося электрона;

б) пары π~ — π⁺-мезонов в поле покоящегося протона.

220. Протоны с кинетической энергией T налетают на непод­вижную водородную мишень. Найти пороговые значения T для следующих реакций:

а) р + р->р + р + р+р; б) ρ + ρ->ρ + ρ + π°.

220. Водородную мишень облучают π-мезонами. Вычислить пороговые значения кинетической энергии этих мезонов, при ко­торых становятся возможными следующие реакции:

а) π- +р-> Κ+ + Σ-; б) π° + ρ->#⁺ + Λ°.

220. Найти странность S и гиперзаряд Y нейтральной элемен­тарной частицы, у которой проекция изотопического спина T_s = = +V₂ и барионный заряд В = +1. Что это за частица?

221. Какие из нижеследующих процессов запрещены законом сохранения лептонного заряда:

     1. п-+ p + e~ + v; 4) p + r->M+v;

     2. π+-νμ⁺ + £- + £⁺; 5) μ⁺->£+ + ν + ν;

     3. л"-ν μ~ +ν; 6) /(" μ~ + ν?

222. Какие из нижеследующих процессов запрещены законом сохранения странности:

     1. π- + ρ->Σ~ + Κ⁺; 4) и + р->Λ° + Σ+;

     2. π^- +ρΣ+ +/С~; 5) + Ξ~ + Κ⁺ + Κ~\

     3. _η- + ρ-*Κ⁺ + Κ- + η; 6) /С~ + ρΩ- + + K⁰?

223. Указать причины, запрещающие нижеследующие про­цессы:

     1. Σ~->Λ°+π~; 4) Α + ρ->Σ+ + Λ°;

     2. π- + ρ-νK⁺ + Κ- 5) π-->μ- + £+ + έτ;

     3. /C" + tt->Q- + /C⁺ + /C°; 6) μ--**- + ν_β + ν_μ.

ОТВЕТЫ И РЕШЕНИЯ

1. ϋ = //2τ=3,0 км/ч.

2. (υ) = 2υο(υί + ν₂)/(2νο+υχ+υ₂)

3. β

   £

   2 7 0 -,1

   <г;>/шт = 15 с

'J

4. a) IO см/с; б) 25 см/с; в) Z₀= г) 2,5 и 0,7 см/с²»

5. (rj-r₂)/l T_i-T₂ I = (V₂-V₁)/! V₂-V₁1-

6. v'=yv$ + v²+2v₀v cos φ?=» 40 км/ч, φ' = 19*.

/ У

7. M==T at _W9 —3,0 км/ч.

: (I -VllV'*)-¹¹²-I

1¾. ft=arcsin (1/η) + π/2= 120\ 1Л0. I=VofV2(1-sin ^jO¹) = 22 м.

11. / = (¾ + г>₂) K ^1¾/^ == 2,5 м.

12. ί = 2α/3ϋ.

/

4

/

						/
					/
				у	/
		Xy
wX
С i						ч
	2	3	H	5	В	7	t

¢)

Рис. ί<

1.13. Из рис, I, а видно, что скорость сближения точек ^rA и В равна Ό — и cos α, где угол α зависит от времени. Для встречи точек необходимо, чтобы были выполнены два условия:

τ %

J (v — a cosa) H = U § ν cosa dt = ux_f о о

где τ—искомое время. Из этих двух выражений следует, что

1.14. ^xi — ^x2 = /— (* +τ/2) =0,24 км. Навстречу поезду со скоростью V = 4,0 м/с. \

^1.15. а) 0,7 с; б) соответственно 0,7 и 1,3 м.

j IiV₂-I₂Vi 1

^υ\Λ-^νΙ

17. CDt=IlVn²-I-

18. См. рис. 1, б.

(ο)=πΚ/τ=50 см/с; б) | (ν) | = 2Я/т = 32 см/с; в) | <w> [=2яЯ/τ²

_t O₁Z₁ + V₂I₂

16. t_m =

^миа —¹

10 CM/C2.

(1 — £/2τ) ο₀ί при t ^ τ; [1 + (1-*/τ)²] ο₀ί/2

при ^ τ.

/1.20. a) v=a(l— 2at)_t w = —2aa = const; 6) Δ^= 1/cc, s=a/2os.»

1.21. a) *=о</(1—^/2τ); б) 1,1, 9 и 11 с; в) S =

Соответственно 24 см и 34 см.

22. a) O = Gt²*/2, α> = α²/2; б) <o)=tcc/s/2.

23. a) s = (2/За) ojj^/2; б) ί = 2 KtWa.

^1¾ a) ί/=— л^/а²; 6) v=ai— 2bt]> w = — 26j, o=Ka² + 4W a>=26; в) tg a == a/2bt; r) <v>=ai —WJ, | <v> | =Va²+^².

25. а) y = x—х²ос/а; 6) o=aKl +(1 — 2a0²» a> = 2aa=const; в) ^₀= 1/a.

26. a) s-αωτ; 6) π/2.

27. O₀ = K 0+я²) ω/2b.

    I		I I
    		1 .·: I I ι	I
    		I V I I , ^t у	I ^r ' I 1
    		$	г г

28. ffmct

    Ct

    ⁱD

    a) r = v^ + g*²/2; б) <ν>^ν₀££ί/2, ,(ν)^vq-zS^/^j

(j.2| a) r = 2(o₀/g) sin α;

б) h — (vl/2g) sin²,a, / = (0½) sin 2a, a = 76^s;

в) у = χ tg a — (g/2o§ COS² a) x²;

r) jRi = cos a, =cos² a.

30. См. рис. 2.

31. /=8/ι sin a.

32. 1.33. At =

    = U с.

    Через 0,41 или 0,71 мин в зависи­мости от начального угла.

2v₀ sin (fly ϋ·₂)

_N g COS O¹₁ -{- COS Ov

(1.34.) a) x—(a/2vo) у²; б) J^ao₀, w_t

Рис. 2.

= cPy/V 1 + (ay/^_t W_n = CpQ)/ 1 + (CiyIv₀)*. 1.35. а) у = (bj$a) x²; 6) # = V²Iw_n = ^/Jz^rш²- w\ = (a/6) [ 1 + (хЬ/а)Ц^3/2 .

1.37. w = aV 1 + (4лл)²=»0,8 м/с²' (1.39) tga = 2s/_JR.

Y.40. а) α>₀=α²ω²/£ = 2,6 м/с², ш_(а|=асо²=3,2 м/с²; б) к>_миа =

άω² Y1 — (R/2a)² = 2,5 м/с², = + a \^г 1 - R*/2a² = ± 0,37 м.

41. R — cP]2bs, w=a Vl + ^bs^/αψ.

42. а) ay = 2ao², tf=l/2a; б) ш = £у²/<?², R=a?/b.

43. ο = 2#ω = 0,40 м/с, α> = 4#ω²=0,32 м/с².

(1¾) a; = (o/i) Kl+ 4a²/⁴ = 0,7 м/с².

45. ω=2κην/1 = 2,0 · IO³ рад/с.

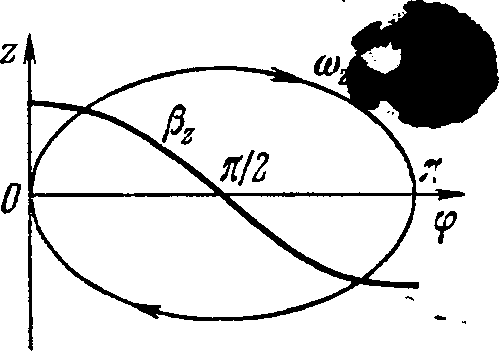
45. Рис. 3.

    w

    центру колеса;

    г) <ω>=2α/3=4 рад/с, <β) = ^3α?=6 рад/с²; б) β = 2|/*3α5 = = 12 рад/с².

46. f=JT(4/a) tgcs=7 с.

47. <ω> = ω₀/3.

. 1.4¾ а) φ = (1 —ω₀/α; б) o=o₀e-< •

50. ω_ζ = + }/ 2¾ sin φ⁴, см. рис. 3.

51. a) y = v'²/$x (гипербола);

    5. у = \/2χ;χ/ω (парабола).

52. а) иJ_i=OⁱJR = 2,0 м/с², вектор

направлен всё время к

6. ш

   s=8/? = 4,0 м.

1.53. а) Уд = 2^= IO см/с, ν_β = V 2 wt = 7 см/с, ⁼ ^

= 2w V1 + (at²/2R)²=5,6 см/с²,

— ^2/2//^=:2,5 СМ/С².

1.54.>Я_д=4г, R_B=2V2r.

!.55. ω=|/ω? + ω|=5 рад/с, β = 0)^2 =12 рад/с².

(ΐ5δ) а) К 1+'(Μ/α)*=8 рад/с, β=α К 1 + (2W/a)*= 1Д рад/с²; б) 17^е.

175/. а) ω== у//? cos a = 2,3 рад/с, 60°; б) β = (ϋ//?)^ tg рад/с².

Ь53. ω = CD₀ Kl +(βοίΜ)² = 0,6 рад/с, β = β_α /1+^ = 0.2 рад/А .^5¾ Am = 2mwf(g + ш).

1.60. W:

то + тх + щ

mi -j- m₂

F =

/7¾ — & (Щ~\~ ^т2)

= и |Л+(1 —^2/^)2^=2,5 см/с²,

(1 +к)щ m₀ + Zra₁ + т₂ ^2g'

1.61. а) F= mjtn,g c.as а к_лт₁₊к,щ

J " ^т2 ^mI 4" ^rnI

ί.62. £ = [(η² — 1)/(η²+1)] tga=0 16.

1.63. а) mjm\ > sina-f fecososi_6) m Itrij <sina—fecoscs; в) sina — &соза< < sin a 4- k cos a.

(\ .64.⁴ W₂ = g (η—sin otf—k cos α)/_(η + 1) = 0,05

65. При t sc t₀ ускорения w₁=w₂ = at/(mi + m₂); при t^t_Q Wf^kgm₂Jm_l, W₂ — (at—km₂g)Jm₂. Здесь Z₀=^gm_l (m₃ + -|-ш₂)/йт_:·. См. рис. 4. -

66. tg2a = — 1/&, a = 49°; f„._IH = = I₁O c.

67. tg β=^; ' Т_шт = mg (sin a +

+k cosa)/j/l+^²·

- ν ^mZ² cos a _Л //2¾³ cos a

65. a ν= . ₉—; 6) s = _g g _д ^ ' Vry^rTin⁹ⁱ n^r ' ⁷ 6fl oinⁱ 01—

,4^69^ ν = V (2g/3a) sin a.

70. τ = К2//(Зш+

71. ay Wj = —— ILJ^Ji

Щ + Щ

Am^m₂

(g —w₀).

m_t + m₂

ш₀ =

1.72. w = 2* (2η —sin a)/(4r)-f- 1).

173 w — + (^1-^2)

* χ ¹ 4/77^2 + /770 (m₁-\-m₂)

^74. V_xp = 2lmMf(M — m) t².

^1.75. (4 + η)/3^ (2 — η) = 1,4 с.

76. H = 6/ιη/(η + 4)=_ί0,6 м.

77. w_A = g/(\ +ηctg²^), +

78. ш.

    ш

    макс

    w=g V21(2 + k + M/m). 1.79_ν w_uliH=g (I —£)/(1 +&)·

= g (1 + k Ctg Gt)/(ctg Ct — k)<

1.81. w=gsin оо cos сс/(sin²cc + пц/т^

rog sin ос _т

M+ 2т (I — cosa) ^β

1.83. a) I <F> J =2 j/2 mu²/jx/?; б) |<F>| = ™sy_f. |Г84>2,1, 0,7 и 1,5 кН.

85. a) W=^gY l + 3cos²fl, 7=3mgcosfl; б) T = mgV3; в) cos θ = 1 /j/З, A = 54,7°.

86. ¢=^53³.

87. ft = arccos(2/3) <=w48⁹, v = Y2gRjb.

88. ε = 1/(Η//^ω²~ I). От направления вращения не зависит.

Ϊ.90. S=¹I_zR V(kg/w_x)*—I=QO м.

91. о^сс У kg/a-

92. T = (ctg θ+ω²^) mg/2.

93. а) Рассмотрим малый элемент нити на блоке (рис. 5). Вследствие его невесомости dT~dF_T?=k dF_n и dF_n = Tdoo. Отсюда dT/T=k da. Проин­тегрировав это уравнение, получим k = (\n η₀)/π; б) w = g (η — η₀)/(η + η₀).

i) F = (mvyR) cos² α.

95. F = —/πω²!*, где г-радиус-вектор частицы относительно начала коор^ динат; F = Zmo² V χ²+у²·

96. a) Δρ = m%t\ б) ] Δρ J =— 2m

97. a) p = at³/6; 6) s=aT*/\2m.

1.82. яу =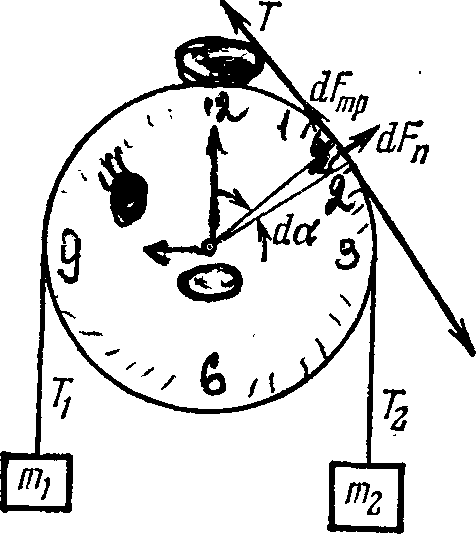

T+dT

Рис. 5.

U98. s = (ωί — sin Ы) F^ты², см. рис. 6. 1.99.-^ = π/ω; s=2F₀/wco²; г>_макс = F(,//mo.

1.100. а) и = и₀е ^irI^m_i t-+co; б) v = Srfm_i S_nord= ; в) (и) = η-I

Со

η In η

1,101. t= , .

v₀v In (ν₀/υ)

102. s=~tga, и_мак_с ^{sin α α} · Указание. Чтобы привести

уравнение движения к виду, удобному для интегрирования, надо представить ускореняе как dufdt и затем произвести замену переменных по формуле dt = dxfv.

102. S = ¹IqQ 't—toflm, где to=kmgfa — момент времени, с которого нач­нется движение. При t^t₀ путь s = 0.

103. ν' = v₀/Vl + ku$/mg.

104. a) v = (2Ffm®)sm (ωί/2); б) As = SFfmGp_t (υ) =AFfKma.

105. ν= v₀/(\ + cosφ). Указание. Здесь = — w_x, поэтому υ = = — V_x+const» Из начального условия следует, чю Const = Ii₀- Кроме того, V_x = V cos φ.

106. w=[ 1 —cos (IfR)] RgfL

107. а) ν = VZgRiS; б) cos A₀^ , где

108. " При ncU включая и отрицательные значения, ry_CT = (mv²/a)^lK^l~ⁿK

109. Если (i>²R > g, то имеются два положения равновесия: ^f=O и — = arccos (gfafiR). Если tfRcg, то положение равновесия только θι=0. Пока существует одно нижнее положение равновесия, оно устойчиво. При появлении же второго положения равновесия (оно всегда устойчиво) нижнее положение становится неустойчивым.

110. h ^ (cos²/u) sin ф = 7 см, где ω — угловая скорость вращения Земли.

111. F = Tn Vg² + ωV²+(2ν'ω)²=8 Η.

112. F_K0? = 2m(tfr Ϋ1 + (с/₀/шг)² = 2,8 Η.

113. ¾) w' = &R; 6) F_m=mtfr VVRfryi-X.

114. F_a6 = mo)²RV5f9 = 8 Η, F_scop = %maj²R Vb + SgfZtfR = 17 Η.

115. a) F=2mv® sin φ = 3,8 кН, где ω —угловая скорость вращения Земли вокруг собственной оси; б) F = та (ω/? cos φ ± 2v) sin φ, F₊ = 33 кН, F^ =25 кН, где знак плюс соответствует движению с запада на восток, знак минус — наоборот, R — радиус Земли.

116. Отклонится на восток на расстояние χ ^ %ω/ι γ2hjg = 24 см. Здесь ω-·угловая скорость вращения Земли вокруг собственной оси,

117. A = F (г₂—Γι)==— 17 Дж.

118. А=таЧУ8.

119. F — 2as V 1 + (*/#)²·

120. A=mg(h + kiy

121. A = — kmglj(\ — k ctg а) = — 0,05 Дж.

122. F_Mim = (mi + m₂f2)kg.

123. Л = — (1 —η) ryngift = — 1,3 Дж.

124. (P) =0, P = mg(gt—^₀Sina).

125. P = mRat_t <P) = mRatf2.

126. a) (P) = —kmgv₀/2 = ~2 Вт; б) Р_маКс = - ¹Itfivl

127. А = ¹Jzmto² {г\ — η) = 20 Лж.

128. A_mn^kk(Al)², где £ = ^2/(^1+¾)-

129. Л=3т^/4а» AU ^mg/2а.

130. а) /·₀ = 2α/6, устойчиво; б) F^_KZ = b^/27a². См. рис. 7·

102. а) Нет; б) эллипсы, отношение полуосей которых α/6 = V^P/⁰^» ^тож^ эллипсы, но с а/Ь = $/а.

103. Потенциальным является второе поле сил.

104. 's=bl/2g (sin α + & cos α), A =— (£-J-Igct);

105. ^7//2; s_MaKc=ff.

U 36. и = ²/з /gh/3* 1.137. и_ичн = /5^/; T^3mg. - 1.138. t = l²/2voR.

139. Δ/= ( 1+/1 +2kl/mg) mg/k.

140. i; = /l9g/₀/32 = l,7 м/с. '

1 141. Λ = , . ,Il^c0s^ . -0,09 Дж.

2 (sin Φ+& cos ϋ) COS Ό¹

142. Λ = κ/2η(1+η)/2(1—где <η=/?2ω²/κ.

143. w_c = g (т± — m₂)²/(mi -f-/тг₂)².

145. r = (g/<o²)tgfl = 0,8 см, T = mg/cos ¹O¹=S Η.

146. a)F_Tp = mg[sina + (o)²//g)cosa] = 6Η; 6) ω </g(*—tg «)//(!+*tg α) = 2 рад/с.

147. a) V = б) Г = μ (ν* — v₂)²/2, где μ = ■= Hi₁Tn₂Km₁ т₂).

148. Я = Я +

149. £ = μ (of + t/§)/2, где μ = m^m₂/(m₁ + m₂). -

150. P = Po-K^g/, где P₀ = ZTZV₁-^m₂V₂, /72 = /?*! + //½; r_c = v_Qt-fg'²/2, где V₀= (/Tc₁V₁ + m₂ v₂)/(mj + т₂).

151. O_c = XYyitn₁Km_l + w₂).

152. а) /_ма*с = 'о + ^7и> 'мин — б) l_mKc = i+2m₁F/yi(m_i+m₂)_t /_ΜΗΗ='ο·

153. а) Δ/ > 3mg/x; б) /1= (1 + κ Δ l/mg) mg/8x = 8mg/K*

154. V₁==-mv/(M—m), v₂=Mv/(M-m).

- ice ^tU . ^m^

W=V₀- дг^ч; V_nep=V₀+ _(M+m)2 U.

, 14 2т _оч m(2iW + 3m)

^|Л5в· ^{0 νι =} ~Ж+Ш^{Щ 2) v}^ (M+m)(/H+2m) ^i-¹ + + т/2 (Λί + m) > 1.

157. ρ = ²/₃m 1^7=3,5 кг · м/с.

158. Ap = т V^gh (1 + η)/(1 —η) = 0,2 кг · м/с.

159. а) 1 = TJ-^—Γ; 6) F = — ^m^ ^d^

M +/n ' ' Λί+m ^

157. l = /nl'/2/W.

158. τ=(ρ cosa — M Ϋ2§1 sin a)JMg sin ct.

159. a) w = (2Ai/m)/g/sin(^/2); 6) η^Ι—m/Λί.

160. h=Mv*l2g(M + m).

161. 1) A=-Hgh_t где \K = mMj(r.i +M)\ 2) Да.

166. ν = 1,01 + 2,0] — 4,0k, м/с.

167. AT = — μ (v_t — v₂)²/2, где μ = Znjm₂Am₁ + ^).

168. a) r\=2m_l/(m_l + m₂); б) ц=Am^m₂!(m_x-\-m₂)K

169. a) /Tz₁Zm₂= 1/3; 6) Hi₁Zm₂ = I +2 cos 6 = 2,0.

170. η = ¹I₂ cos² α ==0,25.

171. С'_макс = 0 (ι + /2 (η -1)) = 1,0 км/с.

172. Будет двигаться в ту^ же сторону, но со скоростью и' =

= (1 — Vx —2η) ϋ/2. При η < 1 скорость¹ у' ^ ηυ/2 = 5 см/с.

166. ΔΓ/Γ = (1 +/n/Λί) tg² θ + m/M — 1 = — 40%. ' ,

167. а) ρ = μ Υυ\ + υ\\ б) T = ^ιΙ₂μ{ν] + ν\). Здесь μ = т^т₂1 (т^ + т₂).

168. sin ^_m3KC = Щ/Щ.

169. ν' =—ν (2 — η²)/(6 — η²). Соответственно при η меньшем, равном и большем /2.

178. Пусть в некоторый момент t ракета имела массу m и скорость ν (относительно интересующей нас системы отсчета). Рассмотрим инерцнальную систему отсчета, имеющую ту же скорость, что и ракета в данный !момент. В этой системе отсчета приращение импульса системы «ракета —выброшенная порция газа» за время dt есть dp = m rfv+μ dt ■ u = F dt. Дальнейшее очевидно.

179. ν——u In (/По/т).

180. m = m₀e"^^/w.

181. a = (Ufv₀) In (т₀/т).

F . то P

178. V = —In г , W =

μ т₀ — μ( * т₀ —μ/ *

178. V= FfM, (1+μ///»_α), W= F/m₀(l+μ///η₀)².

179. ν = V2gh In (Ilh).

180. N=21iVajb.

181. M = ¹I₂WgVot² cos α; M = (mv^ftg) sin² a cos a = 37 кг · м²/с.

182. а) Относительно всех точек прямой, перпендикулярной к стенке и проходящей через точку 0; б) | ΔΜ\ = 2mvl cosa.

183. Относительно центра окружности. | ΔΜ ) =2 Vl — (g/ω²/)² tngljib.

184. |ΔΜ\ = hmV.

185. M^nmvlt². . . ...

186. m=2kr\/v\.

187. 00=/2^7/008^.

188. F=m®lr*/r\

189. M_z = Rmgt.

190. M = Rmgt sin α. He изменится.

191. M' = M — [г_ср]. В случао, когда р = 0, т. е. в системе центра инерции.

198. M = ¹I_zImv₀.

199. вмакс mv\/Yl\* Решение удобно проэести в системе центра инерции.

200. T = 2nyM/v^z=225 суток.

201. а) В 5,2 раза; б) 13 км/с, 2,2.10-4 м/с².

202. Т = п V(r + R)^z/2yM. Достаточно рассмотреть движение по окруж­ности, радиус которой равен большой полуоси данного эллипса, т. е. (r-\-R)/2~* по Кеплеру период обращения будет тем же.

203. Падение тела на Солнце можно рассматривать как движение по очень вытянутому (в пределе вырожденному) эллипсу, большая ось которого практически равна радиусу R земной орбиты. Тогда по Кеплеру (2τ/Γ)² = = [(#/²)/#Р> ^рД^е τ—время падения (время половины оборота по вытянутому

эллипсу), Г —период обращения Земли вокруг Солнца. Отсюда τ=774/2 = с= 65 сут.

Ic204. Не изменятся.

J .205. I=VyM (Т/2π)².

1.206. a) U — ym₁m₂/r; б) U = —y (mMjl) 1η(1+//α), F=ymM/a (α + Ο­Ι .207. M = m У2ym_cr_xr₂/{r_x + r^_t где /п_с—масса Солнца.

208. E = T + U = — ymm_c/2a_> где т_с —масса Солнца.

209. r_m = ~—[\ ±/ΐ—(2 — η) η sin²a], где η = г^Цут₀ т_с— масса Солнца.

^ь210· ^HH^iV^c/^o) [У ¹ +(^lvIIy^mC)²- ¹J^ где /л_с—масса Солнца.

211. а) Рассмотрим сначала тонкий сферический слой радиуса ρ и массы

δΜ. Энергия взаимодействия частицы с элементарным поясом 0S этого слоя есть (рис. 8)

dU = — у (т δΜ /21) sin ft dft. (*)

Для треугольника OAP по теореме косинусов I²=р² + г²—2рг cos ft. Най­дя дифференциал этого выражения, преобразуем формулу (*) к виду, удобному для интегрирования. После интегрирования по всему слою найдем 6U = — ут δΜ//·. И наконец, интег­рируя по всем слоям шара, получим U = — утМ/г; б) F_r = — дИ/дг = = — утМ/г².

211. Рассмотрим сначала тонкий сферический слой вещества (рис. 9). Постровм конус с малым углом раствора и вершиной в точке А. Площади участков, вырезанных этим конусом в слое, dSt: dS₂=r\ : r\. Массы же выре­

212. занных участков пропорциональны площадям этих участков. Поэтому силы притяжения к ним частицы А равны по модулю и противоположны по направо лению. Дальнейшее очевидно.

ι
	/φ M

3

'Fi

(Im₁^dS_j

dm₂ ~ dS%. Рис. 9.

3 D

-дП

Рис. IO_j

1.213. A=—s/₂ymM/R.

1214 G=<! ~(^/Я³)г при г ^R.

(уМ/г*)т при г ^R; ~^zl₂(l—r²/3R*)yM/R при г ^ft

уМ/r при г ^R. См. рис. 10,

215. G = —⁴/з^ур1. Поле внутри полости однородное.

216. р = ³/₈ (1— r²/R²)yM*/nRK Около 1,8-10® атм.

217. 1.214. G=| -{

     а) Разобьем сферический слой на малые элементы, каждый массы δ/η. Тогда энергия взаимодействия каждого элемента со всеми остальными W=—ymbm/R. Суммируя по всем элементам и учитывая, что каждая пара взаимодействующих элементов войдет в результат дважды, получим U = —ym²!2R; б) U= — 3ym²/5R.

3/2

2я

-г

1.218. At-

_ С 4,5 сут (6 = 0),

VyM 3Δ/-/2/- + 6 ι 0,84 ч (δ =2).

219. щ : W₂: W₃ = 1 : 0,0034 : 0,0006.

220. 32 км; 2650 км.

221. h = R!(2gR/vl — \).

222. h= RigRlv²-1).

223. г =VyM (772л;)² = 4,2- IO⁴ км, где M и Г — масса Земли и ее пе­риод обращения вокруг собственной оси; 3,1 км/с, 0,22 м/с².

224. 0 км/с,

     M = (^Jt²R³IyT²) (1+Τ/τ)²=6· 10^ кг, где Г —период обращения Земли вокруг собственной оси.

1.225. о'=^ +

T ¹VR ~ R² у ¹ T

= 4,9 м/с². Здесь М — масса Земли, Т —ее период обращения вокруг собствен­ной оси.

226. В 1,27 раза.

227. Убыль полной энергии E спутника за время dt есть — dE = Fv dt. Представив E и ν как функции расстояния г между спутником и центром Луны, преобразуем это уравнение к виду, удобному для интегрирования.

В результате получим τ ^ (/η—l) m/aVgR·

226. V₁ = 1,67 км/с, ϋ₂=2,37 км/с.

227. Au = VyMjR (1-/¾ = —0,70< км/с, где M и R-масса и радиус Луны.

228. Av = J^gi? ()^2-1) = 3,27 км/с, где g—нормальное ускорение сво­бодного падения, # —радиус Земли.

229. r = nRf(l = 3,8 · IO⁴ км.

230. A^ym (M₁IR₁+ M₂IR₂) = 1,3 · IO⁸ кДж, где M и Я-масса и ра­диус Земли и Луны.

231. v^V 2v\ + (Vi-\f V²_i^ 17 км/с. Здесь ^ = M₃ и Я —

масса и радиус Земли; V^yM_cIr_f M_c-масса Солнца, /- — радиус орбиты Земли.

226. I = ZaF₂Imw= 1,0 м.

227. N = (aB — bA)k, где к —орт оси ζ; / = | аВ — ЬА j//Л² + £².

228. 1=\аА — ЬВ |!VA² + B².

229. Z⁷_paBH = 2/⁷. Эта сила параллельна диагонали AC_f а точка приложе- ния ее расположена на середине стороны ВС.

230. а) /=VsroJ²; б) / =¹I^m (а²-}-б²).

231. а) /=!/2^6^ = 2,8 г-м²; б) I =*i_umR*. 1.249. I = ^lUmR².

241. / = (37/72) тЯ² = 0,15 кг-M²

242. / = ²/₃т£².

243. a) <d=gtlR(\ + Ml2m); б) T=mg²t²/2 (1 +Mfim).

244. T = ¹I₂Tng_i w₀=gmr²II.

245. ω= sin φ/ш/.

ι 24β ο I ^2-fflilg T_i ^ m_t (m + 4m_a) ¹^^to- P (_{Ш1 + та + т}/2)^ ' T₂ т₂(т + Ьт_г)·

1 247. /4=- ^²~-^m^ ^kmIg^2t* m + 2 (m_} + m₂)

248. n = ( 1 + £²) (&lRl$nk (k +1) g.

249. t = ZI_i(S)Rfkg.

250. < ω) = VaW₀.

251. Р = 2т#х/#/(Л1 + 2т).

252. a) fc ^²/? tg α; 6) T = *f_umg*t² sin² a.

253. a) T=Ve^ff^=IS H, $ = *f₃gfR=5. IO² рад/с²; 6) P = y_zmg4.

254. w' = ²/₃(g-w₀), F = ^lf_zm (g — w_c).

255. w=g sin a/(l + Ifmr²)= 1,6 м/с².

!.256. F_mKz = Zkmgfi2-Zk)\ w_mKC = 2kg/(2-Zk).

, 257 д) a, F(c.osa-rfR) ^ F²t²(^a-rfRf

257. a) w- _{m{1 + ?)} , б)Л- 2m {1+β) '·

258. T¹ = Vio^ffW-

•1.259. w = 3j (M + 3m)/(M + 9m + //tf²).

260. a=

mt (m_t + m₂) ' 2m_x (m_x + m₂)

260. To₁ =/7("¾ + ²/?"¾); W₂ = ²I₁-Jχ.

261. a) t = ^lIz¹^QRjkg'* 6) /4 = -Ve^ffzwO^jR^a-

262. ω = l/l0g(tf + r)/17r².

263. = γ ¹JsgR (7 cos α-4)= 1,0 м/с,

260. V₀ = V^rSgR,

261. Ύ = Trvti¹.

262. T = y₁₀mv² (1 + W²/R²).

269. N = ¹IumtoW sin 2ft.

270. cosft = ³/₂g/cD²/.

271. Ax = ¹Izka.

272. 1/=(0(,///1+3m/Ai-

273. SMu²

     v,6)F = _T

     (1+4 Af/3m)²

     3m+4 Al

     F = ^kp²Iml = 9 H. 3m—4M

1.274. a) v'=·

1.275- a) V = (Mlm) V²Isgl sm (al2); 6) Ap = MV¹Ugl sin (a/2); в) х^²/₃/, 1.276. а) ω = (1 + 2т/Μ) ω₀; 6) A = ¹l₂m<x>lR²(\ + 2mlM).

dt ' (O)₁- (O₂)².

2 Iii₁ + т₂ hh

2т₁ -f m₂ I₁M₁ + Ι₂ω₂

2mi ^_{4 λΤ} Ui₁M₂R dv'

φ'; б) Л^ =

277. а) φ =

278. 

     Рис. IU

     а) ω =

б) Л==

/1 + /2 ' 2 (Z₁+ Z₂)

277. ν' = ν(4 — η)/(4 + η), ω= 12и//(4 +η). При η = 4 и η>4.

278. а)Л₉₀о = 1/2/^/(/ + /₀), Л₁₈₀О = 2/^//; б) N = +1₀).

279. ω = /2^/7 = 6,0 рад/с; F = Tngl_fJl = 25 Н.

280. а) M = ¹I₁Imayl² sin ft, M_z = M sin ft; б) ] AM | = Vi₂^/² sin 2ft; в) N=¹I₂^m(X)²I² sin 2ft.

281. а) со' = т£г//ш = 0,7 рад/с; 6) F =

= mco'²/ sin ft = 10 мН. См. рис. 11.

277. ω = (£+ω) l/nnR² = 3- IO² рад/с.

278. ω' = ml Vg² + W²I/ω = 0,8 рад/с. Век­тор ω' составляет с вертикалью угол ft = = arctg (w/g) = 6°.

279. F' = ²/₆m#W// = 0,30 кН.

280. F_m8KC = = 0,09 кН.

281. N = 2mlv/R = 6 κΗ·μ.

282. Рдоб === 2jm/iVtf/ = 1,4 кН. На такую величину сила. давления на наружный рельс возрастет, а иа внутренний—уменьшится.

283. р = аЕАТ=2>2· IO³ атм, где а—коэффициент теплового расширения.

284. а) ρ ^ O_mArfr = 20 атм; б) ρ ^ 2o_mAr/r = 40 атм. Здесь a_m —предел прочности стекла.

285. п = /2а_ш/р/я/ = 0,8 · IO² об/с, где —предел прочности, р—плот­ность меди.

286. ίΐ = /σ_ί7ί/ρ/2π# = 23 об/с, где G_m- предел прочности, р — плотность свинца.

287. JC Ymgl2itd²E = 2,5 см.

288. B = ¹ItF₀IES.

289. T = ¹IzmtoH (l-r²/l²)_y Al = ¹I₃₉U²IyE, где ρ-плотность меди.

290. AV^r = (1—2μ) Fl/E = \,6 μλι», где μ — коэффициент Пуассона меди.

291. а) At = ¹I₂Pgl²IE; б) AV/V = ({-2μ) AljL Здесь ρ-плотность, μ — коэффициент Пуассона меди.

1.299. а) AWV=-3(1-2μ)ρ/£; б) β = 3(1-2μ)/£.

300. R = i/_QEh²/pgl²=0,\2 км, где ρ —плотность стали·

301. а) Здесь N не зависит от х и равеи N₀. Интегрируя дважды исход­ное уравнение с учетом краевых условий dyjdx (0)=0 и у (0) = 0, получим y = (N₀/2EI) χ²* Это уравнение параболы. Стрела прогиба K = N₀l²/2EI_t где /=aV 12.

б) В данном случае N (x) = F (1-х) и y=(F/2EI) (I — χβ) х²\ λ = №/3ΕΛ где / то же, что и в предыдущем пункте·

300. Л=/Ч³/48Е7.

301. а) λ = ³/2Ρgl*IEh²\ б) X^/₂pgl^/Eh². Здесь ρ —плотность стали.

302. λ = ⁹/δβρI^bJEh²_t где ρ —плотность стали.

303. а) ^ = (Ifinr³ArG)-N; б) φ= (21/кгЮ). N.

304. N = K (d* — d\)Gq)/32l=0,5 кН · м.

305. P = V₂JtA⁴Gqxo= 17 кВт.

306. N = ¹I₂^m (r$-r*)/(ri~rl).

307. i/=1/₂тЕ&²/р = 0,04 кДж, где р —плотность стали.

308. а) i/ = Ve^²i³p²g²/^; 6) U = ²I₃Kr²IE (Alβ)². Здесь ρ — плотность стали.

309. л ^VeJi²ZtS³E/i = 0,08 кДж.

310. U = ¹I_lKr^²Il = I Дж.

311. U = ¹I₂G^r²Il².

312. м = VzP (pgA)² = 23,5 кДж/м³, где β — коэффициент сжимаемости.

313. pi>p_2> U₁ < Плотность линий тока растет при переходе от точки 1 к точке 2.

314. Q = S₁S₂ V2gAhj(Sl — S²₁).

315. Q = S V^2gAftp₀/p.

316. υ = V2g (h_x+/i₂p₂/pi) = 3 м/с, где pi и ρ₂ — плотности воды и керосина.

317. Л = 25 см; /_маКс = 50 см.

318. h = ¹/₂v²ig — h₀ = 20 см.

319. p = p₀-J-pg/i (1 —tff /г²), где #i<r<#₂, р₀ —атмосферное давление.

320. A = ¹I₂PV³Is²I²_t где р —плотность воды.

321. τ = Y"2hjgS/s.

322. и = ω/ι /2///1-1.

326. F = 2pgSA/ι=0,50 Η.

327. F = pgbl (2h — l) = b Η.

328. N =PlQ²Im² = OJ H ■ м.

329. F = pgh(S — s)²/S = 6 Η.

330. а) Параболоид вращения: z = ((d²/2g) r²_t где ζ—высота от поверх* ности жидкости на оси сосуда, г —расстояние от оси вращения; б) р = р%-\- -f- ι/₂ρω²ή.

331. Ρ = πηω²/?4/Α = 9 Вт.

1 ЧЧ2 d-D ^{1П Ь332}· ^U-^Uoln (R_lfR₂) ·

,.388. а, б) N^r^^L·.

334. а) Q = Vtfrcw₀R²; б) T = ¹^nlR²PVl; в) Ρ_τρ = 4πη/υ₀; г) Δρ = 4ηίυ₀/β².

335. В левом конце трубки дополнительный напор Ah = 5 см сообщает кинетическую энергию жидкости, втекающей в трубку. Из условия ри²/2 =»

= PgAh получим u = /2gA/t=l,0 м/с.

334. Искомое отношение равно е^аЛ*=5.

335. V₂=V_i ^Гг9Л =5 мкм/с.

3 г jg η2

334. d = Л/ — = 5 мм, где р₀ и ρ — плотности глицерина и

V (Р — Po) Ро£

свинца.

334. / = In лг = 0,20 с.

18η

334. ν = с /η (2 —η) = 0,1с, где с —скорость света.

335. a) P=α (l +)/4—3β²); б) Р = а (/П^+/4ЙГ²). Здесь β = 1//с.

336. /₀ = /1^(1 — β³ sin² ft)/( 1 — β²) = 1,08 м, где β = ν Jc.

337. a) tgiV^-^^- _у отсюда ft'= 59°; б) S = S₀ — β² cos² ^ = = 3,3 м². Здесь β = vjc.

338. v = c у - = 0,6- 10» _M/Ce

339. I₀=CM^f ]Л—(Δ//Δ/')² = 4,5 м.

340. s=сА/1 — (Δ^ο/Δ^)² = 5 м.

341. а) Δ^ο = (//и) Y1 — (и/с)² = 1,4 мкс; б) /' = //l—(и/с)² =0,42 км.

342. l₀ = vMjY\ — (vjcf = 17 м.

343. Z₀ = /Ax₁Ax₂ = 6,0 м, и=с/ί^Δ^/Δ^ = 2,2 · IO⁸ м/с. ^Ыб(К \+ (kjcMf *

351. Частица, двигавшаяся впереди, распалась позже на время Δ/ = = /β/с (1 — β²) = 20 мкс, где β = vjc.

352. a) ; б) t_A-t_B={\-V\-(vjcf) I₀Jv или ^-^=(¹+^¹"^)²)

353. a) t (В) = I₀Jv_i t (B^f) = (I₀Jv)Y \-{vJcf\ б) t (A) = (I₀Jv)V(ν Jcf, t (A^t) = Ufv.

354. С «точки зрения» /(-часов см. рис. 12.

A^f

β-θ-θ-Φ-θ-θ-θ* θ-Φ-θ-ώ-θ-θ-Φ-^

Рис. 12.

351. *=(ΐ-]Λ-β²)^/β, где β = ν^.

352. Для этого необходимо убедиться в том, что при tsi—h—к> О ^и M^t = V₂-V_i > 0.

1.357. а) 13 нс; б) 4,0 м. Указание. Воспользоваться инвариантностью интервала.

_ У(у_х-У)*+УЦ1-У*Ю

¹^³⁵⁸- * 1 -V_xVfc² ·

359. а) о = If₁-+¾= 1,25с; б) v = (v₁ + v₂)f(\+V₁V₂Ic²) =Q$\c.

360. /=/₀(1-β²)/(1+β²), где β = vfc.

361. а) ν = Vvf+ Vl; б) ν = V+ ^ — [V₁V₂Ic)².

362. S = Ai₀I/ ^⁸+O-P²) _где

V (1 — β²) (ι -V²/с²)

359. tgft' = "Г ^s^J где β = Vfc.

^ъ cos ft — Vjv ^г

359. tg ^ = V^tVIc²V^-(Vfc)².

360. a) w' = w (1 — β²)^3/2/(1 — βυ/с)³; б) w' = w( 1—β²). Здесь β = Wc.

361. Воспользуемся связью между ускорением ш' и ускорением ш в системе отсчета, связанной с Землей:

«/=( ι-νψη-w .

Эта формула приведена в решении предыдущей задачи (пункт а), где следует положить V = v. Проинтегрировав данное уравнение (при a/ = const), получим

v = w'tfY \-\~(w'tfc)². Искомый путь I = (Vl +(Wife)²— 1) C²Jw^f= 0,91 светового года; (c—v)fc = y₂(cfw^ft)² = 0A7%.

359. Имея в виду, что v = w't/Vl + (Wtfc)², получим 0

360. т/т₀ ^ 1//2 (1 — β) ^ 70, где β = vfc.

361. ν = с

где с —скорость света. Здесь исяоль- зовано определение плотности как отношение массы покоя тела к его объему,

359. (с— г;)/с=1-[1+(т₀с/р)²Г^1/2 =0,44%.

360. ν = (cfr\) /η²-1 = V₂C V^ 1*372. А = 0А2т&² вместо O_fHm₀C².

373. V = ¹I₂C /3 = 2,6. 108 _М/Св

374. При ε<1 отношение TVm₀C² <⁴/₃ε ^ 0,013.

375. ρ = /Г (T + 2/п₀с²)/с = 1,09 ГэВ/с, где с —скорость света,

376. F = (Ifec) VT (Г + 2/?2ос²), P = TIfe.

377. ρ = 2nmv²f(\—v²jc²).

378. tF=fci///nJc²+F^ai⁸, I = /(m₀c²/F)² +с²**_^/f.

379. F = HibC²fa.

380. а) В двух случаях: F Ц ν и F J_ ν; 6) F=/?ζ₀νν/]Λ — β², F^ =

= m₀w/( 1 — β*)³/², где β = и/с.

382. ε' = ε/(1-β)/(1+β), где $ = Vfc, V=³/₅c.

383. E² — p²c² = mlc^y где m₀ —масса покоя частицы.

384. a) T = 2т₀с² (/l + Г/2т₀с²- 1) = 777 МэВ, p = /v_am₀r = 940 МэВ/с; б) К = с /77(Г + 2т₀с²) = 2Д2 · IO⁸ м/с.

385. М₀ = /2т₀ (Г+2т₀с²)/с, 1/= с/77(Г + 2ет₀с²).

386. Г = 2Г(Г+2т₀с²)/т₀с²=1,43. Юз ГэВ.

387. £_lMaKC= ^mS + ^m"~(^m2 + ^m3)³ _С2, Частица /¾ будет иметь наи-

Im₀

большую энергию в том случае, когда энергия системы двух других частиц т₂ и т₃ будет наименьшей, т. е. когда они движутся как единое целое.

ι ооо , 1 — WmA^2ulc _π

382. V C = —-—. Воспользоваться законом сохранения импульса

1 +(mjm₀)^^c

(подобно решению задачи 1.178) и релятивистской формулой преобразования скорости.

1. m = pl/Ap/p₀ = 30 г, где р₀ — нормальное атмосферное давление,

2. P = V₂(PiTyr_l-Ap) = O_jIO атм.

m₁/m₂ = (i —а/М₂)/(а/M₁-1) = 0,50, где a = mRT/pV.

^2Л' ^{р =} RT (In₁IM₁ + т₂/М₂) ^{= 1} '^{5 Г/л}' *·' 2.5. а) ρ =^₁ + v₂ + V₃) R TlV = 2,0 атм; б) M = (V₁M₁ +V₂M₂+ ν₃Μ₃)/(νχ + + v₂ + v₃) = 36,7 г/моль.

2.6. Г= Γοη' (η²—1)/η (η^/2—1) = 0,42 кК. 27 _Λ = ^ΪΠη

8. p = p₀e7^a/V-

9. f=(V/C) In η = 1,0 мин.

10. AT = (mg+p₀AS)l/R = 0,9 K-

2.И. а) Г_мзКС = ²/₃ (р₀/#) /pi/За; б) Г_маКС= р₀/ерЯ.

12. р_мв„ = 2/?/o7V

13. dT/dh = MgIR = 33 мК/м» " 2.14. dT/dh= — Mg(n—\)jnR.

    15. 0,5 и 2 аТм.

    16. a) Zi = ЯГ/Mg=8,0 км; б) h^^RT/Mg=0,08 км.

15. р_ид = р#77М = 280 атм; p = ptf 77(М —р&) —ар²/М² = 80 атм.

16. a) T = a(V — b)(\+Ti))/RV(r\V + b) = l2>2> К; б) р = — — 01/1/2 = 9,9 атм.

17. α = V² (T^t₁P₂ — Т₂р₁)/(Т₂ — T¹₁) = 185 атм · л²/моль²; 6 = 1/ — /? X X (T₂ - Т₁)/(р₂ - pi) = 0,042 л/моль.

18. κ = V² (V -b)²/[RTV³-2а (V - b)²].

19. T>a/bR.

20. i/ = pF/(v-1)=10 МДж.

IIS

15. AT = ¹I₂Mv² (у-\)fR.

16. T = T₁T₂ (P₁V₁^P₂V₂)KP₁V,T₂ +P₂V₂T₁)) ρ = (P₁V₁ + P₂V₂W₁ + V₂).

17. AU = —ρ₀ν AT/Tq (у— 1)= —0,25 кДж, Q^f=-AU_f

18. Q = Ay_i^y- 1)-7 Дж.

19. Л = ЛАГ = 6,60 кДж, AU = Q-RAT= 1,00 кДж; y = Q/(Q — R&T) =

с= 1,6.

15. Q=vRTq (1 — 1/я) = 2,5 кДж.

^r v₁jv₂-1) +v₂ (vi-i)

34. с_к=0,42 Дж/(г - К), с_р = 0,65 Дж/(г · К).

35. A = RT (η— I— In п). .

36. ^' = ρ₀1/₀1η[(η + 1)2/4η].

37. γ = 1 + (я— l)/(Qf$RTo— In η) = I ,4.

38. См. рис. 13, где У— изохорический процесс, р —изобарический Г — изотермический, S — адиабатический.

о

й)

V

34. а) Γ=Γοη^(ν"^1)/ν = 0,56κΚ; б) Л' = ЯГ₀ (η^(ν~^1)/ν— 1)/(γ- 1) = = 1,6 кДж.

При адиабатическом сжатии дольше в « = (r|^{v 1} — 1 )/(γ — 1) 1 η rj = = 1,4 раза. I

34. Γ = Γ₀[(η+1)ν4η]^{ν"^1)/2.

35. v = }^r2yRT/(y— 1) M = 3,3 км/с.

36. <2 = ΛΔΓ(2-ν)/(ν-1)·

    45. С_п = Й(п-у)1(п-\)(у — 1); C_n <0 при 1 <п<у.

    46. C = R(n-^y)/(n — i) (у—\)= —4,2 Дж/(К ■ моль), где « = 1ηα/1ηβ.

    47. а) ρ=Λ(η-ν)ΔΓ/(«-1) (у-1) = 0,11 кДж; б) А = -RAT/(n- 1) = = 0,43 кДж.

- 2.48. а) А/У = аУ2(п²-1)/(у--1); б) A =V₂aV% (η²-1); в) C = ¹I₂RX

X (γ+ΐ)/(γ —1)·

49. a) C= -tf/(_v-l); 45) ΓΚ<^ν_:1)/2 = const; в) Л=2ЯГ₀ X

Χ(1-η^(ν"^1)/2)/(γ-1)-

49. а) Л = (1-а) ЛАГ; б) C = RKy-l) + R (1 -а); С <0 при а> >Y/(Y-1).

50. a) A = AU(y-\)/a; Q = AU [1 +(γ- 1)/α]; б) C=tf/(y-1) + Λ/α.

Рис. 13.

X_aJf Ь g ^х^лллиг, (L^JiL J

49. a) C = C_y+RJaV; б) C = C_y+Rj( 1+aV).

50. a) C=yR/(y-i)+aRjp₀V; 6) MJ = p₀ (V₂-V₁)Ky-I); A = ₌ P₀ (V₂-V₁)^a In (V₂IV₁); Q = YPo (V₂- VMy -1) + α In (V₂JV₁).

51. a) C = C^Rr₀AxV; 6) Q=aC_p (K₂-V₁) + /^ In (V₂JV₁).

52. a) V<r^aTl^R = const; б) =const; в) V-ar = const.

53. а) Л ='α In η — RT₀ (η — 1)/(γ — 1); 6) pV4^a^-^l^^v = const.

54. ^ = In ^^+α^-, где α и 6 - постоянные Ван-яер- Ваальса.

V b

49. = CLlV_i-CLlV_i = Q_tW кДж; б) Q = RT In ^=-.=2,,8 кДж.

50. a) T (V-bf^Cv =const; 6) C_p-C_y= _l __{2q (V}__t)8/Rryr

51. MT= —Λ/^ . _T7\ =—3,0 к.

V KK_i(K₁^K₂)

49. Q = v²a (^2-^)/^2 = 0,33 кДж.

50. n = p/kT = 1 .!Of. см"®; (/> = 0,2 мм.

51. ρ = (1 + η) m/?77VWV = l,9 атм* где Μ —масса моля азота N₂.

52. n = (pJkT—p/m₂)/(l — Hi₁Jm₂)= 1,6 · IO¹⁹ см~³, где mi и т₂ —массы моЛекул гелия и азота.

53. p = 2timv² cos² ΰ¹ = 1,0 атм, где т —масса молекулы азота.

54. i = 2J(pv²Jp-1) = 5.

55. v/v_KB = V(Г£2)Щ; а) 0,75; б) 0,68.

/ — 3)67¹ для объемных молекул,

t (3N— 5/₂) kT для линейных молекул. Соответственно 1/2 (AZ^r — 1) и \J(2N—*/₃). - ..

2.69. a) C_v=V₂R_i γ=⁹/₇; _б) C_y=(W-IJ₂) R_t γ = (6W-3)/(6^-5); в) C_K=3(W-1)K, γ—(Ν —²/₃)/(N — 1).

2 70 AjQ- / 1/(3^ — 2) для объемных молекул, \ ij(sn-⁹j₂) для линейных молекул. Для одноатомных молекул AJQ = ²J_bt

2.71. Ai = — ^_v/) ^{= 32 г}/^м°ль; = 2/(cyk^ — 1) = 5.

.2.72. a) i =2 (C_pJR-1) = 5; б) i = 2 [C/R + l/(«-l)] = 3_t где η = ¹J₂-по­казатель политропы.

73. γ = (5ν₁ + 7ν₂)/(3ν₁+5ν₂).

74. Увеличится на ApJp = Mv²JiRT =1,2%, где I = 5.

75. a) V_kb=Vzrtjm=0,47 км/с, <е>=з/₂£г=б,о.to-²* д_ж;^) _Гкв== — zv2ktjnpd3=0a5 м/с.

76. В η¹ = 7,6 раза.

77. Q = ¹J₂(Tn²-I)ImRTJM = IO кДж.

78. ®KB=VkT/I = 1,4- IO⁹ рад/с.

79. (ε)_Βρ = 67'₀η²Λ" = 0,7 · IO^-20 Дж. "

80. Уменьшится в η(* + ΐ)/ΐ _{ра3) где}

81. Уменьшилась в η^(Ι"~¹⁾^^ί~'²⁾ = 2,5 раза.

82. C=V_a/?(i + l) = 3R.

■2.83. ^вер —ν"2ρ/ρ=0,45 км/с, (и) =0,51 км/с, г;_кз = 0,55 км/с.

2.84. а) б^ = (8//л)е-^ = 1,6бо/₀;б) bNlN = \2Vbj2R е~^3/20т] = 1,85о/₀.

W. T- Ζ'"'·-°·> -330 К; б) ..yib^. 2.87. T = ^N;_J =0,37 кК.

2*88. _км/с, ρ Щ

89. T = ¹Izmv²Ik.

90. -[-^J^f2^^{mv2f2k7 2}M₁Ctv^dv_x4

91. <и*> = 0, <|^[)=УЖМт.

92. (v²_x) = kTjm.

93. V = Ven <»>· где (у) = Y ZkTfcmi;

⁰⁰ 2 /

89. p = J 2/п^. (¾) = nkT, где dn (о,) = (т/2я^Г)^1/2 п · f ^mv^^2k7 ^o_x.

о

89. <l/u> = V2m/itW=4/n <и>.

90. cfJV/JV = 2π (π&Τ)™^3/2г d&; E_3ep = ¹I₂MT; нет.

91. 6NJN = 3/б/яе~^3/26т] = 0,9%.

92. Искомая величина

OO

ι*

^{ΔΛί 2π} *-^rIz-ZW dz.

N /ттЬ'П³/²

(nkT)

ε₀

Главную роль в значении интеграла играют наименьшие значения ε, а именно

ε =¾= B₀. Медленно изменяющийся множитель Ye можно вынести из-под знака интеграла, взяв его значение при ε = ε₀· Тогда

ANfN = 2 YEjzikT е~ ^^{ik т}.

89. а) р_вер =/3WJm; б) е_пер = £7\

OO

89. dv= ί dn(i/Q/4n)i;cos^ = /i(2^r/nm)^1/2sm^cosO^.

π/2

89. tfv= ί dn(dQ/4n)wcosO = «(m/2jifer)^3/2e~^mir2/2A7,o^arf».

90. F = (kTlAh) In η — Ο,9 · 10~¹⁹ Η.

91. ЛГ_д = (6ДГЫ³Лр£/г) In η =¾= 6,4 . 10» моль"*.

92. η/η₀ =^^a**--^aj^^{7i7jr 7} =1,39.

(OT₂-AI₁) g

89. Не изменится.

»« А

89. (U) = kT. He зависит,

In /t

TT=T'

я-1

2.109. M = ^pln η._

(Ρ — Po) (rj — r\) ⁰⁾² '

1. = Y (2RTI Ml*) In η =280 рад/с.

2. a) dN = n₀e-^arS/kT4nr*dr; 6)

в) dN/N = (a/nkT)^d/2e"^ar2/kT 4nr*dr; г) увеличится в η^3/2 раза.

3. a) d/V = (2rr/z₀/a^3/2) е"^⁷' ^O^r б) U_BQp = i/₂kT. 2.^13. Во втором случае.

114. а) η = I — ti^] ~~^v = 0,25; б) η= 1 — rt¹^—¹ = 0,18.

115. 8=(1-η)/η = 9.

116. η= 1-27^(7^ + 7¾.

117. η = 1 —я¹"^ = 60%.

118. TJ=I-я—<^{1 —}

119. η=1—(/ί + γ),/(1+γ/ζ).

120. я In я *

     В обоих случаях η= I

2.121. В обоих случаях η= I

2.122. η= 1 — -V-^-

' я In я

пУ—1

; б) η = 1 ~

2.123. а) η = 1 — γ —-—_г, . —

' ¹ г ^Y — 1 ' ¹ γ (/г— 1) /гУ"1 *

2.124. а) η= I ГГТ λ t

^{7 1} я — 1 + (γ — 1 )п Ьт η

2 125 л (T-I)Inv

Д125. η-_{τ1ην + (τ}„_1)/(γ__1} .

2.126. η= (T-I)In/.

Рис. f4.

^У{П~¹⁾ ; б) η-l "-1+(Т-1Ппя

γ(«—1)

τ In я + (τ — 1) γ/(γ — 1) '

127. η= 1-2 У+ ^^x

(1+7)(1+/τ)

127. Неравенство jj — ^

0 только усилится, если заменить T₁ иа Г_макс и Г₂ — на Г_ман. Тогда Qi/r_MaKC — —С2/Г_Мин<0· Отсюда

Qi^gL_< Т-^жс-T_mih ^ _{или η<η}

Vl * BiaKc К ар по

127. По теореме Карно MlbQ₁^dTfT. Найдем выражения для ЬА и 6Q_X. Для бесконечно малого цикла Карно (его можно считать параллелограммом 1234, показанным на рис. 14)

-1

я

M = dp ■ dV = (др/дТ) _v dT - dV_t 60ι = dU₁₂ +ρ dV = [(di/,W)_r + ρ] dK. Остается подставить последние два выражения в первое. 10 и. Е. Иродов

127. a) AS = ^p= 19 Дж/(К·моль); б) AS = ^~^ = 25 Дж/(К-моль).

128. я =

129. AS = vR In « = 20 Дж/К.

130. AS= In п = -10 Дж/К-

131. AS = (γ In α —In β) vRj(y — 1)= — 11 Дж/К-

132. 

     Рис. 15.

     S₂-S₁ = VJR (In α ^ΐΩ ^

_t , = 0,5 Дж/К.

V-I/

127. AS= ^twTT?* In τ.

(η — 1) (γ — 1)

127. AS= ^v(V+l)fl ΐη_α = 46 Дж/К-

V-I

127. V_m = yp₀Ja (1+γ).

128. Γ == T₀ + (/?/α) In (V^rZV^r₀)-

129. AS In l(V₂ — b)/(Vi — b)].

130. AS = C_v, In (^₂Zr_i) + ^ In [(V^r₂ — 6)/(V^r₁ — 6)].

131. S = αΤ³/3.

132. AS = m [α In (Tyr₁)+ 6 (T¹₂-T₁)] =2,0 кДж/К-

133. C = Sfn; Cc 0 при η < 0.

134. Г=Г₀е⁽⁵~~^5о)/С, см. рис. 15.

135. a) C=-α/Γ; б) Q = a In (Т\/Г₂); в) Л = а In (T₁JT₂)+ C_v(T₁-T₂).

136. а) η = (η—1)/2я; б) η = (« — !)/(« +1).

137. AS = vR In я = 20 Дж/К-

138. AU = (2Y^_1 — 1) RT₀f(y— 1), AS = #ln2.

139. После быстрого расширения давление будет больше.

140. AS = ViR In (1 + n)+v₂R In (1 + 1 Jn) = — 5,1 Дж/К.

141. О

     AS = Iii_lCi In (TfT₁) + т₂с₂ In (TJT₂) = = 4,4 Дж/К, где T = (M₁C₁T₁ + m₂c₂T₂)J(m\Ci + Hi₂C₂), c₁ и C₂ — удельные теплоемкости меди и воды.

2.153. AS = C_y In ^(TlfJf >0-

к т

Ig 2

2.154. a) P= \J2^M; б) N

80, где т~10 5с—среднее время

пролета атомом гелия расстояния порядка размера сосуда.

W

2.156. Р„ =

mV

N

.; соответственно ¹J_32i ⁵J_32i ²⁰J_32t ²⁰J_32t ^J_32t ι fa.

η ! (Ν —η)! 2'

2.157. P_n——, ,

^п η ! (Ν —η) ί

^Ν' ρ^η (I-p)^N~ⁿ_t где P = VJVο.

158. ά = Υ6/π«₀η² = 0,4 мкм, где n_Q — число Лошмидта; (ti)=\Jrf = = 1,0. 106.

159. Увеличится в Ω/Ω₀ = (1 +ATjT_Q)^tMА/2 = IO^{1l3b 1021} раз.

160. 2.155. Q_iiep = N IJKNJ2) Ι]® = 252. P_м/2 = S_Bep/2^N = 24,6°/₀.

     a) Ap = ^aJd= 13 атм; б) Ap = 8a/d = l,2· 10~³ атм.

158. A=4a/pgd = 21 см.

159. a = ¹JsPod (1 -η³/η)/(η²-1).

160. p=p₀ + pg/i + 4a/ii = 2,2 ^а™' Л- 1,-fii.

161. h=[po(n*-\)+*a(n²-\)!d)!₉g=$ м. ^ ~

2.1«. η=»(Λ —1)/(JV —I); η=1/(ΛΤ + 1).

Qt=Zstn (qH-#TfM) = 2,4 МДж, где <7 — удельная теплота парообра­зования. ^р⁷^⁷¹⁴

Ю—тсАТ) £ р F^w.

190. ft «а ρ ς (i+qM/RT) =20 см, где с—удельная теплоемкость воды,

AT= 100 К» <7 — удельная теплота парообразования воды, Т — ее температура кипения.

190. A=mc(T~T₀) RT 1цМ=2Ъ Дж, где с— удельная теплоемкость воды, Г —начальная температура пара, равная температуре кипения воды (это видно из условия), q—удельная теплота конденсации пара.

191. d =¾ 4αΛί/ηρ#Γ = 0,2

мкм, где ρ — плотность воды.

190. μ=ηρ₀ VMftnRT =0,35 г/(с-см²), где р₀ —нормальное атмосферное давление.

191. ρ = μν^Γ2πβ77Λί =0,9 нПа. 2.195; Ap = a/VM= 1,7. IO⁴ атм. 2.196. P_i я» ρ?. Приблизительно 2- IO⁴ атм.

2.198. в=²⁷/в4Я²71р/Р_Кр = 3,6 атм · л²/моль², & = ι/₈#Γ_κρ/ρ_κρ = 0,043 л/моль, 10* " 291

199. У^_р = ³/₈#Г_кр/Л4р_кр = 4,7 см*/г.

200. (π-f 3/ν²)(3ν — 1) = 8τ_β τ= 1,5.

201. a) V_MaKC = ^tSbmjM = 5,0 л; 6) p_mKC = aJ27b² = 230 атм.

202. Г_Кр = ^sI₂₁CifbR = 0,30 кК, р_ко = ¹UMjb = 0,34 г/см*.

203. т) = ⁸/зЛ^Ркр/рЯ:г_Ко = 0,25, где р — плотность эфира при комнатной температуре.

204. Применим уравнение (2.4д) к обратимому изотермическому циклу 1-2-3-4-5 — 3-1:

T§dS = §d^TJ + §pdV.

Так как первые два интеграла равны HyvTO, то и ^pdV = O. Последнее может

быть только при равенстве площадей I и II.

Заметим, что эти рассуждения не применимы, например, к циклу 1 — 2 — 3 — 1. Он необратим, ибо включает совершаемый в точке 3 необратимый переход из однофазного состояния в двухфазное.

199. ц = с \ t\/q = 0,25, где q — удельная теплота плавления льда; при / = —80 ⁰C.

200. AT= — (TAV'/q) Ap=—7,5 мК, где q — удельная теплота плавле-

*

ния льда.

199. V^f_nn qATjTAp= 1,7 м³/кг, q — удельная теплота парообразования, T = 373 К.

200. р_нп P₀ (I + qMATjRT²) = 1,04 атм, где <7 —удельная теплота паро­образования, р₀ —нормальное атмосферное давление, AT⁴=I_iI К·

201. Amjm = (qMjRT — 1) ATjT = Sy₀.

2.210. р = ро exp

qM ( 1 1 '

Эти упрощения допустимы для не

R \ Tq T

слишком широкого интервала температур, значительно меньших критической.

211. ύ\ ^cpTAVIq² = O_f03, где с —удельная теплоемкость льда, T^273 К, q — удельная теплота плавления.

212. а) 216 К, 5,1 атм; б) соответственно 0,78, 0,57 и 0,21 кДж/г.

213. AS ^m [с In (T₂JT₁) + q/T₂ + RjM\ = 7,6 кДж/К-

214. As ^ Q_mJT₁ +с In (T₂IT₁)+q_napjT₂+RfM = 9,0 Дж/(г ■ К)·

215. AS = mcln (TJT₁) = —10 Дж/К, где с —удельная теплоемкость меди, T = 273 К (при данных условиях лед растает частично).

216. а) При m₂c₂t₂ < m^q лед растает не весь и

AS = т₂с₂ — 1 — In ) = 9,2 Дж/К;

б) при m₂c₂t₂ > m_tq лед растает весь и

AS=-^+e₂ Im₁ In ~ - т₂ In γ¹)= 18 Дж/К.

Tn₁T₁^m₂T₂-Tn₁Qfc₂ т₁ + т₂

211. AS = mq j^j + mc^A— 1 — In -^) = 0,48 Дж/К.

212. C = C_p-qMjT= — 74 Дж/(К ■ моль), где C_p = Ryf(y — 1).

213. AS = qM/T₂ +C₀ In (T₂ZT₁).

2-.220. a) η ««0,37; 6) η ^ 0,23.

221. λ = Δ//1π η.

222. а) Р = е~«'; 6) {t) = \J<x.

223. а) λ = 0,06 мкм, τ= 0,13 не; 6) λ = 6 Мм, τ = 3,8 ч.

224. В 18 раз.

225. %=(2πΝд/Щ²¹* (kT_QjV2np_Q) = M нм.

226. V = τίά²ρ_ϋΝд Y 2у J MRT₀ =5,5 ГГц.

227. а) 0,7 Па; б) 2 - IO¹⁴ см'³, 0,2 мкм.

228. a) M = Yiiid²Tt (v) = 0,74 . 10« _C"i; б) V = ¹J₂Yfnd²n² (ν) = 1,0 χ χ 102« (T¹-CM"*, где n = p₀!kT₀, (υ) = VSRTJnM.

229. а) λ = const, ν — Vf; 6) λ~Τ, v~l//f.

230. а) λ = const, ν увеличится в У ft раз; 6) λ уменьшится в η раз,, ν увеличится в η раз.

231. а) V₉ ν— V-V⁵; б) λ~ρ~^5/7, ν~ρ^6/7; в) λ~Τ~^5/2₃ ν ^ T³.

232. а) λ~ν, v-F-i"+¹^; б) v~p<ⁿ + ^lV²ⁿ; в) λ- ^,_Tl/(l-n)_{t ν}^_Τ(η+ί)/2(η-ί)₉

233. a) C=V₄^ (1+2/) = 23 Дж/(К ■ моль); б) C=Va^ (i + 2) = = 29 Дж/(К · моль).

234. n = n₀e~^t/x, где x = 4V/S(w), <»> = VWT/πΜ.

235. Увеличится в (1+η)/(ΐ+Κη) раз.

236. Увеличилось в α³/β = 2,0 раза.

237. a) D увеличится в ft раз, η = const; б) D увеличится в я^3/2 раза, η — в Yn раз.

238. D уменьшится в я⁴/⁵ ^ 6,3 раза, η увеличится в /г^1/5^1,6 раза.

239. а) л = 3; б) п = 1; в) n=h 2.240.4),18 нм. -

241. d_ArJd_lie= 1,7.

242. ^V₁ 2πηω^3/Δ^_; р = У~2 Wlnd²FifS_iR = OJ Па.

243. η = (1/Α?-1/β!) Αν4πω.

244. Ν = 7₂ίΐηωα⁴ΖΛ.

245. N = ¹I^atp VnMf2RT.

2 246 ц-_-

·^μ 16η£Γ /

247. Г = (X₁T¹₁ZZ₁ + κ₂Γ₂//₂)/(κ₁//₁ + κ₂//₂).

248. x^t/i + Zj/ft/Xi + ia/Xa)·

249. Г (jp) = T₁ (T₂JT₁)^xS¹; q = (α//) In (T₂Zr₁).

250. ΔΓ = (ΔΓ)₀β-«', где Ol = (IIC₁^IJC₂) SkJL

251. 7 = 7^1+(*//) [(TVT₁)³/²-1]}²/³, _где расстояние от пластины с температурой T₁.

2iR^3/2 (т|^/2 —Т^3/2)

²·²⁵²· ^q = Q_nV²IdtN ΥΈ ^^{4,0 ВТ/М2> ГД6 ί==3, d}-эффективный диа- метр атома гелия.

2.253. λ = 23 мм > /, следовательно, газ ультраразрежеииый; ? = (^-ω/θΤ(γ-1) = 22 Вт/м*. где = ^8#Τ/πΛί. T = V₂(T₁^T₂).

2.254. T = T_i+ ,^T' Jlⁱ, In ^Г

In (R₂IR₁) Ri '

²-²⁵⁵-^r=^ri+wik(i-T)·

256. Г = Г₀ + (Я² —r²)w/4x.

257. T = T₀ + (R²-T²)WjbK.

1. Отношение F₉JF_rp равно соответственно 4» IO⁴² и 1 · IO³*; q/m=0,86- 10-ю ^л/кг.

2. Около 2· 1016 Н.

3. dq/dt=³f₂a V2m₀mg!l.

ЧЛ η - _r __ п Vq₂+T₂ VQj

ЪЛГг +V^f ³" VTi+ Гь ⁹ 3.5. Δ7¹ = ^ЯЯо

8Jt⁵V² '

3.6. E = 2,7i — 3,6j, E = 4,5 кВ/м.

37 £_

V2 пв₀(1²+х²)³¹²' .

QO /7 Я

^£ "" 2π²ε₀β² ·

9. E = —f-—оГолГ· При напряженность E^—-— как для

4πε₀ (г +/ ) 4яе₀/²

точечного заряда. £_Макс —— при l = rlV%·

6 V 3 яе₀г²

9. E- ³^

4πε₀Λ^ * qX

3.11. T⁷

4 ne₀R

12. a) E = —; б) £ = l·⁰^ , при напряженность

4ε₀Κ 4е₀ (лг ;

О A^f

12. a) E = ; б) £ = - . В обоих случаях при

4πε₀Γ V^a2 + г² 4πε₀ (г²—a²)

Г^>а напряженность γ,

^ 1V2

12. E= - Вектор E направлен под углом 45° к иити» ^з·¹⁵·^{а) б)}

    16. E= -¹I₃SLrfe_0t

    17. E = — ¹I₃IiGje_0t где к —орт оси ζ, от которой отсчитывается угол О. Как видно, поле внутри данной сферы однородное.

    18. E= -¹I_etSiR²Ie₀.

    19. IQj = ¹Z^Zfye₀, Знак Φ зависит от выбора направления нормали к кругу.

3.20. |Ф| =— 1 — —_г

¹ ε₀ V Vl+ту

нормали к кругу.

21. I Φ I =VaJipr₀ (Л^а — г5)/8о.

22. E_mΚ0 = λ/πε₀/.

23. E = ¹Z₂O₀JE_0t причем направление вектора E соответствует углу φ = π«

24. PoR³

    при г ^ R_y E

    при г ^R; б) E_mKZ

    Po

    Φ = 4nRa.

3 г

3.25. a) ^=-^-(¹

4R j " "" Г2е₀г²

= V₉Potyeo при г _т = ²I₃R.

3.26. q = 2nR²<x_t E = ¹I₂CtIz₀.

и E

3ε₀α г² *

^⁰ (1 — е~^аг3). Соответственно E ^

3.27. E =

3ε₀

3ε₀α г²

28. E = ¹/₃ар/8₀.

29. 1 —

    E=V2^aP/^o» ^гД^е вектор а направлен к оси полости q I. 1 '

3.30. Δφ =

2JiE₀R \ ]Л +(α/Я)² У λ

31. φί — фг~ "о 1πη = 5 кВ,

32. (P = ¹I₂ORlE_0t E = ¹UOIE₀.

33. =г\ При I —> 0 потен·

    φ=—(/f+WO²--!), Е = —(\

2ε₀^χ' 2ε₀\

циал(р = |£, ^JL; _{при />й} потенциал где

<7 = σπ#².

31. y = oR/TiE₀.

32. E=—а, т. е. поле однородное.

3.26. a) E= — 2a(xi— у)); б) E=-~a(yi+x}). Здесь i, j —орты осей ж, у. См. рис. 16, соответствующий случаю а> 0.

Рис. 16.

3.37. E = — 2 (OATi + fck)^ E = 2 Va² (χ² + _{+ а)} Эллипсоид

). Знак Φ зависит от выбора направления

вращения с полуосями ]Λρ/α и /φ/б. б) При φ > 0 однополостной гиперболоид

вращения, при φ = 0 прямой круговой конус, при <р<0 двуполостной гипер­болоид вращения.

R.

3 R*

3.38. а) фо — ^_p ·; б) <p = <p₀(l

Sne₀R

Y\ +3 cos² О, где E_r- радиальная, а Е$-

4пг₀г³

— ρ

3.39. E = уEⁱ_r +E^

перпендикулярная к ней составляющие вектора Е.

3.40. E_z =

4πε₀

ρ 3 cos² O¹ — 1 _г P 3 sin O¹ cos Φ

E _L ρ в точках,

лежащих на боковой поверхности конуса с осью вдоль ζ и углом полураствора θ, для которого cos ft= 1/^3 (#1 = 54,7°, ft₂ = 123,5°). В этих точках E = E_χ =

= рУ'2

4 Л E₀A³ 3.41. R-у 4_πεο£_ο ·

ql

и _п „ λί

f> ·

42. 0)¾^ cos ft, E^ ₀

^т 2 πε₀/· 2πε₀/·²

42. ψ= _t^ql _ £* =

^p где H_v-Проекция

4πε₀ (/?² + *²)³⁷² " 4πε₀ (R* + x²) вектора E на ось Графики этих зависимостей показаны на рис. 17. При

. ₀ и E_x

2л&о^³ *

Я¹ „ π _ Я¹

* I > Я потенциал φ

^cc			ГХ
\		/		4^a
	\ У \ /	в /

Рис. 17,

V
	<7

Рис. 18.

3.44. φ

E γ — —

jc \

3.45. φ

2 e₀

с/

2ε₀ Vx² + R* at

1

Vχ²+ R- / '

etRz

2ε₀(χ² + £²)^3/2

См. рис. 18.

При Xp-R по­

2ε₀ (λ'² + R?f²

тенциал ^tP^⁵-^и E ^' 2пе х? ' ^ГД6 P^^z ® формулах для φ знак

плюс соответствует пространству со стороны положительно заряженной пла­стины, а знак минус —со стороны отрицательно заряженной пластины.

3.46. a) F = O; б) F= ; в) F

3 P²

= 2,1 - 10-16 н.

2πε₀/⁴

λρ

2леоГ² *

3.47. F =

3.48. φ= — αχ*/-j-const.

49. = —*^SJ +const.

50. φ = — у (йх + bz) + const,

51. ρ — 6ε₀α*.

52. ρ = 2e₀Ayjd²\ E = pd/e₀.

53. ρ = —6ε₀α.

54. q = 41 Уnsokx.

q²

49. Л- _16πεο/ .

50. 3ρ²

    _а) ,Jm=M_lQE-2 (l

' \ 5 K 5 /

3 57 F = ^{2V2^^0g2

3.58. /⁷ =

32πε₀/⁴ '

' 2π(/² + Κ²)^3/3 4πε₀ 4^(1+1/4(^/0²] ⁷ ' 4πε₀

^χ"/τ(^ι~ yr+4(//tf)²)* ³·⁶³· ^cP=T^r-

³⁶⁴ '-T^ (Ι-^+лт)·

b , j 1/Λ—1/α при

¢2= -- ¢1, V= 4Й5Г 1 (1 — A/a)/r при г

66. а) ^₂₃ = AyJd₁ £_i2 = ^₃₄ = ^2^23-" ^б) | Οχ | = O₄ = ¹I₂Z₀AyId* O₂ = 1 O₃1 = = *'₂e₀Aq>Jd.

67. q_x = —q (I-X)Jl_i q₂ = —qxjl. Указание. Если заряд q мысленно «размазать» равномерно по плоскости, проходящей через этот заряд и парал­лельной пластинам, то ясно, что заряды q_x и q₂ не изменятся. Изме­нится только их распределение, и электрическое поле станет простым для расчета.

I. 3.68. dFJdS = ¹J₂O²Je₀.

а²

69. F= _{QO п}„ =0,5 кН.

32л ε₀^²

69. F = ¹UnR²Oye₀. пор

3.71. N = ^Tjj^rp- = 3 · IO³, где щ — концентрация молекул. 3βρ³

3.72. F =

4п²е₀И ·

3.73. a) X = RfV27 б) х = { ^UR ("Р^{итяжение})' '

t 0,29R (отталкивание). См. рис. 19·

Г_я

4

³'⁷⁶· 9внутр = — i? (е — 1)/с, ^наруж = ?^ — 1)/8.

77. См. рис. 20.

78. 8-1

    3.74. P =

    

    3-1 q' = —д.

    Рис. 19.

    E = Kcos^ O₀ + ε² sin² α₀

= 5,2 В/м; tg α = ε tg α₀» отсюда α = 74°; σ' = ⁸°^{(ε 1}} E₀cos α₀ = 64 пКл/м²,

Ψ
I — I
I
I- Е/
ι V ЛУ

0

77. а) φ

78. a)£ = {^p//ef0

EdS=-—-JiR²E₀ cosft

; 6) D dr = — ε₀ (ε — 1) /£₀ sin ft.

I pd/e₀ при /> d_F

ρ/²/2εε„ при /^d, -(dfa + l — fypdfo при /^d.

^б) Ρ'==—Ρ(ε—1)/е, o^f=pR χ

Графики зависимостей E_j^ (χ) и φ (*) см. на рис.21, б) с'=Odie-IVe P'=-P (8-1)/6.

		I
-а о		I а χ
-Г

Рис. 21.

3.81. а) Е = /^р'^{/3ввв При}

I ρΡ³/3ε₀Γ2 при г > R;

X (8—1)/Зе. См. рис. 22.

82. Е = -<*Р/4е₀Я·

83. E= —Po (1 —x²/d²)/e₀, U = ЫР₀]Ъе₀.

84. a) £ι=2ε£₀/(ε+1), £₂ = 2£₀/(ε +1), D₁=D₂ = 2e8₀£₀/(8 + l); б) Ei*= E_0f E_z=Eо/г, D₁ = D₂ = E₀E₀.

85. a) E₁ = E₂ = E₀, D₁ = B₀E₀. D₂=ED₁; б) £₁₌=£₂=2£₀/(8+1), D_x = = 2ε₀£₀/(ε + 1), D₂ = eD_v

86. £ = q/2mo (ε + l)r².

87. ρ = ρ₀ε/(ε —1) = 1,6 г/см³, где ε и р₀ —диэлектрическая проницае­мость и плотность керосина.

88. ^_акс=(е-1)ео£ = 3,5 нКл/м², / = π^²(ε-1)ε₀£ = 10 пКл.

89. а) Воспользовавшись непрерывностью нормальной составляющей век­тора D на границе диэлектрика, получим о'= — ql (ε — \)βπή (ε +1), при I-+ ο σ' 0; б) ^=-9(8-1)/(6+1).

90. £ = ?² (ε- 1)/16πεο/² (ε + 1).

391 £^/?^/2jl(1+8)^r2~^{B вак}УУ^ме'

\ е?/2я (1+ε) г²—в диэлектрике;

^riI-

cp=q/2n&Q (1 + ε) r J

92. σ'=^i (ε—1)/2^8(8+1); при 1-+0 α'

93. ο' = ql (ε — 1 )/2π/-³ε.

94. E₁ = Pfyeod (в зазоре), E₂= — (1 — λ/d) Ρ/ε₀, D₁ = D₂ = Pfyi.

95. ρ' = —2α, т. е. от г не зависит.

96. a) E= — Ρ/3ε₀.

97. E₀ = Vs (8 + 2) Ε.

98. Ε = 3Ε₀/(ε+2), Ρ = 3ε₀Ε₀(ε—1)/(ε+2).

99. E = —P/2e₀.

100. Ε = 2Εο/(ε+1); P = 2^E₀*ε— l)/(e +1). η _1Α1 γ 4πε₀ε^₁

^{31 ь} ~ 1 + (6-1)¾/¾'

102. Напряженность уменьшилась в Va (⁸+0 Р^аз; (е —1)/(ε+·1).

103. a) C=-^_r7-; б) a'= BjJ (¾-¾) +

104. a) 0=80(62-8^5/^^(82/8!); б) р'=— q (ε₂ — z^/dSe².

105. C = AnEQaIlxi(R₂IR₁).

106. При условии E₁R₁Ei_m = e₂R₂E_2m.

107. U = R₁E₁ [In (£2/^1) + (81/82) In (¾/¾)]-

108. С ^ πεο/1η (ί>/α).

109. С sis 2πεο/1η (b/a).

110. С^2ябо8а. Указание. При b^>a можно считать, что заряды распределены по поверхности шариков практически равномерно.

111. С^4ле₀а.

112. a) C_o6ul=C₁-I-C₂-I-C₃; б) C_o6lll=C.

113. a) C = 2eoSl3d; б) C = Se₀Sftd.

114. U ^U₁(\+C₁lC₂)=9 кВ. 3.115; ί/ = £/(1+3η + η(")=:10 В.

£ = σ/2πε₀(1+ε) г* .

¹HB вакууме и в диэлектрике.

3.116. C_x=C (V5 — 0/2=0,62С. Поснольку цепь бесконечна, все звенья, начиная со второго, могут быть заменены емкостью C_xf равной искомой.

117. U₁ = QfC₁ = ЮВ, U^ = qfC^ = 5 В, где <7 = (<Рд-<Рд + £) X X C₁C₂HC₁ + C₂).

118. i/_x = (^₂ — 1 + С_х/С₂), V₂ = (S₁^g₂)I[XJ_rC₂IC₁).

119. я=\Ш₁-^<ё_г\С₁С₂1(С₁ + С₂).

120. φ_Α-φ_β=8 (C^q^ + Q) ' ^ПрЙ У^словйй =

^312Ь ^ 1/с_{1 +} 1/с₂ + 1/Сз ^мКл·

122. q_x = %C₂, q₂ = — ^C₁C₂I(C₁ + C₂).

123. </х = ^C₁ (C₁ - C₂)KC₁ + C₂)=- 24 мкКл, q₂ = ЩС₂ (C₁ - C₂)f(C_t + C₂)= = -36 мкКл, = S (C₂-C₁)= +60 мкКл.

124. φ_Α-_Ψΰ = (Сβ, - C^₁)/(C_j + C₂ + C₃).

125. _φι = ^С₂+|зС₃-^С₂ + С₃) ^ ^

^ ^iCi + ^₂C₂ — ^₃ (C! + C₂)

Cx + C₂+C₃

122. 6) 1^ = (/2 —4) <?²/4πε₀α; в) №

     С_общ = ^2С'^ + ^С'^+^С'>

С1 + С2+2С3 3.127. a) W = (f2+4) q*/4n&₀a; -Y 2 q²j 4πε_Όα.

4πε₀ α

129. \V=—q²fSnE₀L

130. W =q₁q₂/4ne₀L

131. AW=-¹I₂V²C₁C₂KC₁ + C₂) =-0,03 мДж.

132. Q = &²CC₀/(2C + C₀).

133. 3.134. W = W_± + W₂ + W₁₂ =

     Q = ¹I₂C^b Интересно, что полученный результат не завгкит от ^₁,

, Jl + 4πε₀ ^ 2R₂ R₂ J'

135. a) W = 3q²f20m₀R; б) W₁IW₂=Ifb.

136. W = (q²/SnEoE)(lfa—\fb) = 27 мДж.

137. A = (q²lSne₀) (IlR₁-IlR₂). Я(Яо + Я/2) ( 1 1 \

3.138. Л

Si

4πε₀

139. F₁ = σ²/2ε₀.

140. Λ = (ί7²/8πε₀) (1/а —1/6).

141. a) A = q² (χ₂ — ^/^oS; 6) A = e₀SU² (X₂-X^X₁X₂.

142. а) А = ¹I₂CV^2f^K 1 — η)² = 1,5 мДж; б) A = ¹I₂CU²^e (е- 1)/[ε-η X χ (ε— 1)]² = 0,8 мДж.

143. Ap = e₀e (e—\)U²/2d² = 7 кПа = 0,07 атм.

144. h = (e²-I) σ²/2ε₀ε²ρ£.

145. F = kRe₀ (ε — 1) U²Id.

146. N = (ε— \) e₀R²U²IU.

147. I =2nE₀aEv = 0,S мкА.

148. 1^2ле₀(е — \)rvUfd = 0,\\ мкА.

149. а) α = (α!+ηα₂)/(1+η); б) α (а₂ + ηα₂)/( 1 + η).

150. ^₁C₁ + ^f₃C₃-e₂ (Ci+ C₃)

     C1 + C2 + C3

     а) б/₆Я; б) V12R\ в) ³UR.

151. R_x = R {УЗ -1).

152. R = (l+УI+AR₂IR₁) Rifi = 6 Ом. Указание. Поскольку цепь бесконечна, все звенья, начиная со второго, могут быть заменены сопротивле­нием, равным искомому сопротивлению R.

153. Подключим мысленно к точкам Лий источник напряжения U. Тогда U= IR = I₀Roy где / — ток в подводящих проводах, I₀-ток в провод­нике AB.

Ток I₀ можно представить как суперпозицию двух токов. Если бы ток / «втекал» в точку А и растекался по сетке на бесконечность, то по провод­нику AB- из симметрии —шел ток I/А. Аналогично, если бы ток I поступал в сетку из бесконечности и «вытекал» из точки В, то по проводнику AB шел тоже ток //4. Наложив друг на друга оба эти решения, получим I₀ = Iβ. Поэтому R = R₀/2.

139. R = (Pfinl) In (Ь/а).

140. R = p (b — a)/Anab. При b-+ со # = ρ/4πα.

141. p = AnMabl(b — α) С In η.

142. R = pl2na.

143. a) j = 2alUIpr^_i б) R = plAna.

144. a) j = IUfipr² In (//а); б) R_l = IpIn) In (Ija),

145. I = UCIpEE₀ = 1,5 мкА.

146. RC = PEE₀

147. σ = D_n = D cos α; j = D sin α/εε₀ρ.

148. I = US (O₂-O₁)Idln(O₂Ia_i) = S нА.

165. <7 = ε₀ (р₂ — pi) I*

166. O = E₀U (ε₂ρ₂ — 4Pi)l(Pidx+pid₂)_t σ = 0 при ειρι = ε₂ρ₂·

167. g = e₀I (E₂P₂-E₁P₁).

168. p = 2e₀U (η — l)/d² (η +1).

169. a) R₁ = 2nalS²; 6) E = 2naIjS².

170. t= -RC In(I-UlU₀) = Qfi мкс.

171. ρ = τ/ε₀ε In 2 = 1,4 · 10¹³ Ом · м.

172. /=[(η-l)SlR]e-W^RC.

173. U = Sl(n + 1) = 2,0 В.

174. φι-φ2 = (£ι-&) *ι/(*ι + Я₂) - £ι = -4 В.

175. R = R₂-Rv Αφ = 0 у источника тока с внутренним сопротивле­нием /?₂.

176. а) I = а\ б) Ф^ —Ф_£ = 0.

177. V_a-V_b=(S₁-S₂) R₁^R₁ +R₂)=-0,5 В.

178. /! = ^2/(^1 + ^2 + ^) = 1,2 A, I₂ = I₁R₁IR₂ = O_iS А.

179. = + — *)*//]1 при Я >tf₀ U^UqX/L

180. ^=(^2+^1)/(/?!+¾). Ri = RMRi +Rz)-

181. I = (R₁S₂-R₂Si)KRRi +RiR₂ +0,02 А, направление тока— слева направо (см. рис. 3.44).

182. a) I₁ = [R₃ (S₁ -S₂) + R₂ (Si + SsMRiR₂ + R₂Rs + RsRi) = 0,06 А;

^б) ΦA-VB = ^I-¹I^rI=⁰*^{9 В}·

165. / = [£ (Я_а + R_B) + S₀RMR (R₂ + R₃) + R₂R₃].

166. ^β

= — 1,0 в.

187. R_AB = r(r + 3R)l(R + 3r).

188. U = ¹Z₂SQ-е-2//ЯС).

189. a) Q=^kq²RjAt; б) Q = V₂ In 2 ·

190. R = SR₀.

192. Q = I (S — U) = 0,6 Вт, P = -IU= —2,0 Вт,

193. I = U/2R; P_mKC = U²jAR; η = Va-

194. На 2η = 2%.

195. T — T₀ = (\ —U²IkR.

196. R_x = R_lR₂KRi +R₂)= \2 Ом.

197. R = R_xR₂KRi +R₂); QmK = (%iR2 + %*Ri)²№iR₂{Ri +R₂V

198. H = YNrlR = S.

199. Q = ¹I₂CS²RiKRi +R₂) = 60 мДж.

200. a) AW =—V₂CU²v)K η)=—0,15 мДж; ^6) A = ¹I₂CU^KX — η) = 0,15 мДж.

201. AW = -¹I₂ (ε— 1) CU²= —0,5 мДж, Л_мех = V₂ (ε— 1) CU² = O_iS мДж.

202. h^a ¹I₂E₀ (ε— 1) U²Ipgd²_j где ρ —плотность воды.

203. a) q = q<£~^t/e°^eQ; б) Q = (l/a — X/b) ^/8πε₀ε.

204. а) 7 = 7о(1-е-^т^^с) = ОЛ8мКл;б)а = (1-е~^2т/яс)^/2С = 82 мДж.

205. а) I = (U₀jR) б) Q = ¹UCU²₀.

206. ejm = ^rjqR=XS· 10Д Кл/кг,

207. р = Umfe = OАО мкН · с.

208. S = enl (v)jj ~ IO⁷- м, где п — концентрация свободных электрйнов, {ν) — средняя скорость теплового движения электрона.

209. а) t=enlSlI = 3 Mc; б) F=enlpl = 1,0 MH, где р —плотность меди.

210. E = (Ifim₀r) VmfieU = 32 Β/м, Δφ = (//4πε₀) /m/2eU = 0,80 В.

211. а) ρ (χ)=—V_98oax-2/3. б) / = ν₉ε©α^3/2/2ё/т.

212. η = Idje (и++ и^) US = 2,3- ICH см~з.

213. «₀ = ω₀/²/2(/₀.

214. а) = см~з . c~i; б) n = ]/^/r=6« IOT см~з.

215. (η— 1)1 Vrh_i =13 мс.

216. t = E₀x\U!enid² = Afi сут.

217. /=ev₀e°^.

218. / = (е°^—1) enila.

219. а) В = μ₀//2# = 6,3 мкТ; б) B = ^₀R²Ifi (R²+x²f^/2 = 2,3 мкТ.

220. В = ημ₀Ι tg (nln)finR. При nсо B = ^₀IfiR.

221. β = Ayi₀Ijnd sin φ = 0,10 мТ.

222. 

     3.185, /χ = [Я₃ (φι - Фг) + Я₂ (φι —Фз)1/(Я1Я₂ + ад₃+^ι)==0,2 Α.

     U

     Ri + R₂

     идет от точки С к точке D.

     1 =1,0 А, Ток

     β = (π— φ + tg φ) μ₀//2π# = 28 мкТ.

μο£ 4π

224. B ^yi₀IiIjAn²Rr_i где г —расстояние от прорези.

225. β = μ₀//π²£.

3.226. а) β = (μο/4π)(π//Λ); б) β = (μ₀/4π) (1 +3π/2) //Я; в) β = (μ₀/4π) X Х(2 + я)///?·

,_r 3.227. Д = (|1о/4л)/ /2// = 2,0 мкТ.

228. а) ΰ = (μ₀/4π)/4 + π²//^ = 0,30 мкТ; б) β = (μ₀/4π)/2+ 2π + π² χ χ///? = 0,34 мкТ; в) β = (μ₀/4π) |/"2 ///? = O_vIl мкТ.

229. а) β = μ₀ί*/2; б) £ = μ₀* между плоскостями и B = 0 вие плоскостей.

о оол и ί ^{виутри пластииы}>

О.ZoU. JD = \ . ,

I μο/α вие пластины.

231. В том полупространстве, где находится прямой провод, Β = μ₀Ι/2пг_ш ^ — расстояние от провода, В другом полупространстве B = 0.

232. Даииый интеграл равен μ₀/.

233. Β = Γ^/2μ°»^{Γΐ ПРИ}

I VaHo fjr] R²Zr² при г^Д.

231. B = ¹^oIjl]* т. е. поле в по­лости однородное.

232. /(Γ) = (6/μο)(1+α)Γ«-ι.

233. В = μ₀η//)/Ί + (2R/1)².

234. а) β = ν₂μ₀«/ О - я/У*² 4" S²), где χ > 0 вие соленоида и х < О

виутри соленоида; см. рис. 23; б) X₀=R (1 — 2ц)/2 |/η(1 —η) 5¾ SR.

3 238 Л = i ^/h) Vl-mR)² = 0,29 мТ, г < Я, \ (μ₀/4π) 21 jr = ОДИ мТ, г >

239. η = 8- IO².

240. Φ = (μο/4π)/=1,0 мкВб/м.

241. Φ = Φ₀/2 = μ₀η/5/2, где Ф₀ —поток вектора В через поперечное се­чение соленоида вдали от его торцов.

242. Φ = (μο/4π) 21 Nh In η = 8 мкВб.

243. р_т = 2π#³£/μ₀ = 30 мА · м².

244. р_т = ^f₂NId² = O_iS А· м².

245. а) В = = ^{7 ΜκΤ}ϊ ^б) Pm = ¹I^IN (а² + аЬ + Ь²) = 15 мА ■ м²,

246. a) B = ¹Z₂^₀OteR; б) р_т = ¹Z^nateRK

247. В = ²/₃μ₀σωjR = 29 пТ.

248. P_m=Z¹IbqKto; p_m/M = q/2m.

249. Β = ν2μο<*ω#².

250. F_mZFq = μο^ο^² = (νZc)² = 1,00 · 10~β.

251. a) F₁ = Ii₀I^R = 0,20 мН/м; 6) F₁ = ^₀I²Znt = 0,13 мН/м.

252. Б== Zid²Q_mZARI = S кТ, где о_т — предел прочности меди.

253. B = (2pgS/I)\gft=\0 мТ, где р —плотность меди.

254. В = AmgifNIS = 0,4 Т.

255. a) F = 2μ₀//₀/л (4η² — 1) = 0,40мкН; б) Α = (μ₀αΙΙ₀Ζη) X X 1π[(2η + 1)/(2η-Γ)]==0,10 мкДж.

256. R да /μο/εο (In η)/л = 0,36 кОм.

257. 

     Рис. 23.

     In (14-b/a).

     3.258. F₁ =

     μο 2/i/a 4л 6

     F₁ = V₀I²Zn²R.

259. F₁ = B²^nо.

260. Во всех трех случаях F₁ = — β|)/2μ₀. Сила действует вправо. Ток в листе (проводящей плоскости) направлен за чертеж.

261. Ap = IBfa = 0,5 кПа.

262. ρ = μ₀/²/8π²Α*.

263. ρ = ¹^ort²/³-

264. I_up = V^cIF„р/ЦолЯ.

265. P = v²B²d²R;(R + pi/5)²; при R = pd/S мощность Р = Р_ткс = =^ ¹Ifl²B²ClSfp.

266. U = ¹U^I²In²Rrne = 2 пВ.

267. U = IBleE= 2,5-IO²⁸ м"¹; почти 1 : 1. 3.2G8. U₀ = \/г\В = 3,2 . 10-3 м²/(В-с).

269. a) F = 0; б) F = (μ₀/4π) 2/p_m/r², F [| В; в) F = (μ₀/4π) 2/p_m/r², F fir.

270. Ρ=(μ₀/4π) 3nR²Ip_m/(R² + x²f^f2.

271. F = 3l^₀p_lmp_2mlnl* = 9 нН.

272. Г ^ 2Bx³^₀R² = 0,5 к A.

273. B^r = B Yμ² sin² α + cos² α.

3.274. a) φ H dS = Ji^²S cos θ-(μ— 1)/μμ₀; 6) φ B dr = (Γ— μ) Bl sin Φ-

/У

J

0

S

Рис. 24.

3.275. a) Γ_ηθΒ = χΙ; 6) /;₆ = χ/;

в

B

противоположные стороны.

276. См. рис. 24.

277. B= ^μι,^μ2 JL.

μι + μ₂ яг

276. Β = 2Β₀μ/(1+μ).

277. Β = 3Β₀μ/(2 + μ).

278. H_c = NIll = 6 кА/м.

279. H 6β/μ₀πίί = 0,10 кА/м.

280. При b R проницаемость 2яДβ/(μ₀/Υ/ — 6Б) = 3,7 . 10*.

μ

276. Я = 0,06 кА/м, μ_Μ3κο^Κ°· 1°⁴·

277. Из теоремы о циркуляции вектора H получаем

В

μ₀ΝΙ μ₀π^

# = 1,51 -0,987Я (кА/м).

6 b

Кроме того, между В и H имеется зависимость, график которой показан на рис. 3.76. Искомые значения H и В должны удовлетворять одновременно обоим уравнениям. Решив эту систему уравнений графически, получим H^ 0,26 кА/м, B^ 1,25 T и μ = β/μ₀#^4. 10».

276. Fa* ¹UxSB²Iμ₀.

277. a) x_m = MV^\ б) χ = μ₀Γ_Μ3ΚΟ/^/ΐ/Β_δ⁹ = 3,6.10-4.

278. A ¹UxVB²_fP₀.

279. S_i = ByVWa .

280. I = BvV(R^R_v), где R_ix = R₁R₂I(R^R₂).

281. а) Δφ = ι/_2ω2α-/7ΐ^ = 3,0 нВ; б) Δφ \'₂ωβα² = 20 мВ. С

282. \ E dr = — ¹Z₂QB d²= —10 мВ. >1

3.292. S_i = ¹U (—I)ⁿ Ba$t_y где п = \, 2, ... —номер полуоборота, которому принадлежит данный момент Л График S_i (t) показан на рис. 25, где t_n =

S_i

/7

B²I² g sin α

/„„„ = а!г, где a = ¹Un₀Iv I InR. μ₀ 2Ia²v

An χ (х+ а) 3.295. S_i ^ ¹U (ωα³£² + 2mg sin mgR sin α

3.296. ϋ = ·

3.297. ш =

298. (P)=¹I₂(Udia²B)VR.

299. B = ¹UqRlNS = 0,5 Т.

= γ 2лп/р.

3.293· ¹пнд 3.294. S_i =

μ₀β/ . Ъ 4- а

З'ЗОО* q⁼ 2nR~ ~Ί)~—(ΐ* ^Т* ^е' ^{от не зависит}·

Рис. 25.

3.301. a) / = J^lnA 2л R а

302. a) S = VjtnRll²B¹; б) Q = VamciJ.

ρ

303. о = · -(1— где α =BH²_tImR.

am ⁴ " <

303. а) По круговому проводнику —по часовой стрелке, в перемычке тока нет; б) во внешнем проводнике —по часовой стрелке; в) в обоих круговых проводниках —по часовой стрелке; в перемычке тока нет; г) в левой части «восьмерки» — по часовой стрелке.

304. I = ^lUidB₀ (а~Ь)/р = 0,5 А.

305. S_im = ¹Una²NaB₀.

306. %_t = *l₂wlBP = 12 мВ. ¹U^oⁿIr при г < а, ^ι/₂μοnla²lr при г > α.

3.311. ω =

З.ЗЭ9. / = ¹AiM^SdZVp ==2 мА, где р —удельное сопротивление меди· 3.310. E = ¹Uab (η— 1)/(η + 1). Я

в Μ.

2т

о з|2 Г. - W²V^{2 r}Iмакс *

313. Q = Vsa²T³//?.

314. I = ¹Uib²-α²)βΛ/ρ.

315. I = Y^nl₀LI\ι₀ =0,10 км. «г I^jlO ^mR

316. L = — _t где ρ и р₀ —удельное сопротивление и плотность меди.

317. j ! _ώ

     f ¹U 1.308. E = I

     X ¹U

     /= —4 In (1 -η) = 1,5 с.

318. 305

     τ = -L = 0,7 мс, где ρ — удельное сопротивление, р₀ — плот*

ность меди.

3.319. I₁ =J^-In η = 0,26 мкГ/м,

320. L=-V^ μΝ*α In j.

321. L₁ = VohIb = 25 вГ/м.

322. L₁ = J^ In (η -1).

JT

320. a) ! = Jia²BlL; 6) A = ¹I₂JiWB²IL·

321. / = /₀(1+η) = 2 A.

322. / = — - = 50 A,

-К-·)

320. /=| [l +(η—I) e-'^].

321. / = ~ (l — e~^iR/2L).

K

320. Z_i=-Ik-, /₂₌

Я Oi+W ^г K (L₁+ L₂) ·

320. In (l +-у).

321. L_ie=JJsfc_nA

2π α

320. a) Li2 «a ¹I₂Vona²Ib; 6) Φ₂ΐ=ν₂μοπα²//6.

321. p_m = 2aRqlv₀N.

322. Li₂BS¹I₂VOnatIP-

323. Z₂=-^ (I-

К

³·³³⁵· ^Q=2R*(1+R₀/R)=^{3 м}"Д^ж·

336. W⁷=V₂MDZ = O₁S Дж.

337. W⁷ = 5Яπ²α²6 = 2,0 Дж, где H = If₂NIfnb.

338. а) IT₃/Ц7^bfnd = 3,0; б) ,^f^² =0,15 Г.

О Л"/JA

336. W₁ = μολ²ω²α²/8π.

337. £ = 5/Кё^ц"=3· 10« В/м.

338. ш_м/ш₉ = SoHoW²O⁴//² =1,1 · 10"¾ , а) £_общ = 21; б) 1_0бщ=1/2.

3.344. L₁₂ = ^^rL₁L₂.

346. ^₁₂ =I₁I₂ cos ft·

347. а) J_cm= — j; б) /_ΟΜ = <7/ε₀ερ.

348. Кроме тока проводимости следует учесть ток смещения.

349. E_m = I_mlE₀toS = 7 В/см.

350. H = H_m cos (arf-J-α), где H_m = V ^²+(ε₀εω)^, а α определяется

формулой tga = 8₀ea)/a.

при г С R_f при г>#.

у ulwil v^ uw иции/^ и .

г, .. ί ¹^Sr

'•351. Jсм = <

I ^яя²/'

Здесь S = p₀n/_mG)² sin ωί. 306

о.ои*. «/ _JCM— , JCM-

353. X_m = Oj /см макс ^я 4ддЗ ·

354. H=^{9 [νΓ}'

4ЯГ³

353. а) Если В (/), то V X E= — OBfOt Φ 0. Не равенство же нулю про­странственных производных Е-поля (V X E φ 0) возможно только при наличии электрического поля.

б) Если B(^)₁ то Vx E= — OBfdt Φ 0. В однородном же поле VxE=O.

в) По предположению, Е = аf(t), где а—вектор, ие зависящий от коорди­нат, /(^ — произвольная функция времени. Тогда —dBfdt = V XlL = O, т. е, В-поле не зависит от времени. Вообще говоря, это противоречит уравнению VxH = ODfdt₉ ибо левая часть его в данном случае оказывается ие зависящей от времени, правая же часть —зависящей. Исключением является случай, когда f(f)— линейная функция, В этом случае однородное Е-поле может быть переменным во времени.

353. Возьмем дивергенцию от обеих частей уравнения VxH = J+dD/d/. Имея в виду, что дивергенция ротора всегда равна нулю, получим O = V-j +

+ -щ (V · D). Остается учесть, Что V · D = р,

353. Возьмем дивергенцию от обеих частей первого уравнения. Так кап дивергенция ротора всегда равна нулю, то V-(dB/d0 = 0_f или -^-(V-B) = O,

Отсюда V >B = const, что действительно ие противоречит второму уравнению.

353. V χ Е = [оВ].

354. E' = [vB].

355. σ = ε₀ϋΒ = 0,40 пКл/м².

356. ρ=—2еоО)В=—0,08 иКл/м³; σ=ε<,αωΒ = 2 пКл/м².

357. B-^iJ=L

4я г³

364. Е' = 6г/г², где г—расстояние от оси t\

CL frv]

364. B^r=—где г—расстояние от осн г\

C¹ г ^Δ

367. a) E =EV^r-—V^2cos2a =9 кВ/м; tg ее' =-M^r, откуда a' ^

V ι-β² /ι-β²

_жБ1·; б) В'=M^= 14 мкТ. _€γ\ β2

367. a) F = ^^=1,4 иВ/м; б) В>=В ΐ/ΊΞΕ^^ _Т.

cY 1 — pa V 1 — β²

α· г=»51°_# ,

370. B^t = BYl-(EfcB)* «530,15 мТ.

371. Пусть заряд q движется в положительном направлении оси я /С-системы отсчета. Перейдем в /С-систему, в начале координат которой этот заряд покоится (оси х' и χ обеих систем совпадают, оси у' н у — параллельны).

1 Q

В /("-системе поле заряда имеет наиболее простой вид: E' = r'_f

4πε₀ г'⁸

11* 307

H В ПЛОСКОСТИ X_t у

Теперь совершим обратный переход в исходную /(-систему. В момент, когда заряд q проходит через начало координат /(-системы, проекции х, у вектора г связаны с проекциями х', у' вектора г' соотношениями

X = г Cosft = X' V \ — (υιcf, у = г sin θ=у\

Кроме того, согласно преобразованиям, обратным (З.би),

E_x = E^rI E_y = EyiVl-(Vjcf.

Решив совместно все эти уравнения, получим

^ул 4ле₀ гЗ (1 — β³ sin² Ф)

Следует обратить внимание на то, что в данном случае (v = const) вектор E -ксшшнеарен вектору г.

370. V = Y^j_2tQlelm = Xb км/с.

371. tga = -2p-"|/

2eV^% '

370. а) х = 2Е₀/а; б) w = qE₀fm.

371. fJ^ + ^-SJ) не.

сеЕ

370. с²

     w ^βΕ

т₀ (1 + T/m₀c*f *

_e£t -

370. а) tgft = у 1 —(щ/с)-, где е и /л₀ — заряд и масса прогона;

HIqVQ

б) υ_χ = V JV 1+(1- Vjjc*) (βΕέ/^ψ.

370. a = arc sin (dB ) ^{= 30}°*

371. a) V = TeBjm= 100 км/с, T = 2nmjeB = S,b мкс;

6) v = clV\ +(WbCjreBf =0,51 c, T= ^2jxmQ ==4,1 не.

eB V I-(Olc^s)

370. a) ρ = qrB\ 6) T = m₀c² {V1 + (qrBjm₀Cf — l); в) да=

371. Г = Tjm₀C². Соответственно 5 кэВ и 9 МэВ.

372. Δ/ = 2π V^rnUJeB² cos α = 2,0 см.

п поп ; 8π²ί7

3.384. /· = 2ρ j sin (φ/2) I, где ρ = -^-sin α, φ= ^

еВ ^Ύ mv cos α

3.385. r_MaKC^ae^tw6, где

U U

3-386. ^_m = .

rB In(^a)' г^аВ^а In (&/А) *

_{0 00}_ 2л~тЕп* V₀B 3.387. a) ^=—J₅- ; б) tga =

qB² ' ^{7 &} 2л£п * 308

3.38S. ^ligyⁱу; при г</ это уравнение упрощается; у =¾

(ZmEfql²B²) ζ².

389. F = mEIfqB = 20 мкН.

390. = tg φ = 6 см.

3.392. а) χ = α (ωί —sin ω^); */ = α (1 — cos ωί), где a = mEfqB², ω = ςΒ Траекторией является циклоида (рис. 26). Движение частицы представляет собой

у

движение точки иа ободе круга радиусом а, катящегося без скольжения вдоль оси χ так, что его центр перемещается со скоростью v = E;B; б) S=SmEigB²I В) (V_x) = Е/В.

3.393. (/ = 2 ^ M² In I-.

/га \ 4д j о

s.m.B^^f'^-u.

3.395. у=t sin ωΛ x = -^^ (sin ω^—ω* cos atf), где a = qE_mfrn. Траек­тория имеет вид раскручивающейся спирали. 3.396. U > 2jt²v²mrAr/e=0,10 MB.

397. a) T=^f-= 12 МэВ; б) V_mhh = ^ =^{20 ΜΓ}«·

K²VfTtr² 4H^V²/?2/'²

397. a) ^=—-^j— = 17 мкс; б) ^^— = 0,74 км. Указание.

N _

Здесь S^ 2 ~Σ^^rt* ^гД^е Уа~"^СК0Р^0СТЬ частицы после м-го Прохожде­нии

^Ν _ ^Ν __

«ия ускоряющего промежутка. Так как N велико, то ^У] =¾ J in.

ι о

397. n = 2nvWfeBc* = 9.

398. ω=ω₀/}^Α l+αί» где id_Q=qBfm₁ a = qBAW[лт²с\

399. V = ¹UrqBfm,. .ρ = г/2.

400. N = WfeΦ = 5· IO⁶ оборотов, s = 2HrN = 8· IO³ км.

401. С одной стороны,

^dP ^eE = J-

dt 2кг dt *

где р — импульс электрона, г —радиус орбиты, Φ— магнитный поток внутри нее.

С другой стороны,, dpjdt молено найти, продифференцировав соотношение ρ = €ГВ при г = const. Из сравнения полученных выражений следует, что ιIB₀Jdt = ¹I₂ (dB/dt). В частности, это условие будет выполнено, если B₀ = ¹I₂(B)₉

397. г₀ = У2В₀13а.

398. dEldr = B{r₀) — ¹I₂(B) = O.

399. AW'=2nr²eB/At = 0,\0 кэВ.

400. a) W = (V\ + (reB/rrioc)² — l) т₀с²\ б) S=WAtIreB. 4.1. а) См. рис. 27; б) (ϋ_Λ-/αω)² + (χ/α)² = 1 и W_v= —

4.2. а) Амплитуда равна а/2, период T = π/ω, см. рис. 28, д; 6} = «=4ω²χ(α — χ), см. рис. 28,6.

Рис. 28.

3. X=U cos (со/-J-ос) = — 29 см, V_x =—81 см/с, где α=γχ% + (υ_χ0/ω)²_β и = arctg (— ϋ_χ0/ωχ₀).

4. ω=ν(ϋΙ-νΙ)Ι(χΙ— xf), a = V(Olx%-vl*i)l(v\-vl)· 4.5· a) <ϋ) = 3α/Τ = 0,50 м/с; 6) (v) = €>alT = 1,0. м/с.

4.6. а) б) | <_v> ) =αω; в) (_у)^IiirJ^_0i0e

ί ^α [л + 1—cos (ω/—mi/2)], л —четное,

\ α [л + sin (со/—ля/2)], л —нечетное. Здесь л—целое число отношения 2ω//π.

8. s = 0,6 м.

9. dP/dx = 1 /π Va²-X².

10. В обоих случаях a ===7.

11. ^макс = 2»⁷³ αω.

12. 47,9 и 52,1 рад/с, 1,5 с.

13. 18 или 26 Гц.

14. a) x²ja²+y²/b²=l, по часовой стрелке; б) W= — о²г.

15. а) у² = 4х² (1 — x²j(X²)I б) у = а (I — 2х²/а²). См. рис. 29.

Рис 29.

8. Τ2 = π Vmfa²U₀* '

9. Т = 4паУта/Ь²,

10. Г = π VlnliF — 0,2 с.

11. Г = 2л; VV/g (η —1) = 1,1 с.

12. Г=2 [π/2 + arcsin (α/β)].

.οι , Ί/"2ΛΓ V^rT=Pn—V^r^zzrTl

8. /=|/ / ^{ JL——_t где η = ш/g·

г α» ί —V 1 —η

8. T = )^4jim/pgr² = 2,5 с.

9. T = 2π У ц (1—η) т/х=0,13 с. •4.24. Г «2π V^rZnAHi+ X_a) .

   25. Γ = 2π V^mM» ^ГД£ κ = ^1^2/(^1"+«г)·

   26. ω = Г о/т/.

   27. Γ=2π VWspg (1 +cosθ) = 0,8 е..

   28. Γ = π )^2//^ = 1,5 с.

   29. a) λ'+(g/β) jc = 0, где χ—смещение тела относительно центра Земли. R—ее радиус, g—нормальное ускорение свободного падения; б) τ=^V Rlg = = 42 мйн; в) Ji = V^r^ = 7*9 км/с.

   30. Γ = 2π V^r^lg-Wj «0,8 с, где | g — w | = /^+tci²—2gm сое β.

4.31,. Γ = 2π/Υх/т—ω² = 0,7 с, ω^/κΛ^ΙΟ рад/с.

32. £ = 4π²α/£Γ2 ==0,4.

33. a) O = 3,0° cos 3,5/; б) 0=4,5° sin 3,5/; в) d = 5,4· сое (3,5/ + 1,0). Здесь t в секундах.

34. F=(m_i-\-m₂)g±:m_ia(d² = 60 и 40 Н.

2Я ωί

36. а) у = (1 — cos о/) tngjy,) где ω = Υκ/т; б) F_MaKC = 2mg, T

37. 0.

    МИН'

    4.35. a) F = mg(^l + ΐψ. cosω/), см. рис. 30; б) сн;

    см.

    ш) а = (ω Y2hig — 1) g/ω* = 20

    (xfroF + afa/vо)^а=1..

36. a) = (1 — cos ω/) ш/ω²; б) у = (ω/— sin ω/) α/ω*. Здесь ω = V κ/л*.

37. ДА_маКс = mg/k = \0 см, E = m-gy26 = 4,8 мДж.

38. α = (mg/κ) Yl+Zhx/mg, E = /ngA-j-m²g²/2κ.

. 4.41. a=(mg/K) Yl +2/гх/(т + Λί)^.

42. Запишем уравнение движения в проекциях на оси χ и */:

* — ω*/, # = — ωχ, где ω = α/т. Их интегрирование (с учетом начальных условий) дает χ = (ν₀1ω) (1—cos (of), у = (Vajid) sin ω/. Отсюда (χ — ϋ₀/ω)² + Это уравнение окружности

радиуса ι>₀/ω с центром в точке X₀ = ^₀/ω, ι/₀ = 0.

42. Увеличится в Yl 4~²/₅ (Я//)² раз. Здесь учтено, что вода до замерзл- вия движется поступательно, и система ведет себя как математический маятник.

Y

4.44. ω

1 +

21

2κ/ \ Mg )'

45. a) T = 2ii YIftg- 1,1 с; б) £ = V₂^a² = 0,05 Дж.

46. rp_m = фо К1 + , £ = ¾^.

47. (T) = ¹Umglbl + ¹Zi₂ZnZ²^J. 4г48. Γ = 4π/ω.

    49. / = ш/² (ω;—gll)!(a>\ — ω|) = 0,8 r-м².

    50. ω = YUtidj + IfptW₁ + h)·

    51. χ = //2/3, T_mni = 2л Vllg j/ З .

    52. Г = л V^rSSzi^r. I_np = h/2.

    53. ω₀ = Υ'ΖααΡβΙ.

" "4.54. ω₀ == Yxi(m+//7?²).

2/rcg cos a

55. ω₀- _{и/ MR + 2mR(X + sin α)} -

56. Г = 2л/3 (R — r)fig.

57. Г = л|/3т/2х.

^; 4.58. ω₀ =/κ/μ, где μ == Hi₁Hi₂Knii + /7½).

1. а) ω = }Λί/μ = 6 рад/с; б) £ = ^1^ = 5 мДж, a = V₁Jid =2 см. Здесь μ = Hi₁W₂Jim₁+т₂).

2. T = 2л Yl⁷Jk у где /' = Z₁Z₂ZfZ₁+ /₂).

3. ω₂/ωι = ]/ΐ+2га₀/т_с^ 1,9, где т₀ и т_с—массы ашов кислорода в углерода.

4. O = S Y2yp₀/mV_0t где γ—показатель адиабаты,

5. q = 4h Yns₀mg (η² — 1) = 2,0 мкКл.

6. Индуиция поля увеличилась в η²=25 раз,

7. χ = (ν₀/ω) sin ω/, где (O = IBYmL.

8. х = (\—cosotf)g/o>², где о^ = IBlΫmL.

9. a) O₀ и α₀ω; б) = -j— ^arctg + nnj, где η = О, 1, 2,

• 4.68. а) φ(0)=~βψ₀, φ (О) = (β²—ω²) φ₀; 6) Z_7t = ^arctg + шг),

где/*=* Ο, 1, 2, ...

ι .V₀1 Γ —я/2, е:ли дг₀>0,

69. a) Q₀ = -^_l а = < .

' ⁰ ω ⁹ { +я/2, если *₀<0;

йу Oq= IX₀1 Yl + (β/ω)*, α = arctg (— β/ω), причем —π/2 < α < O₁ ссла *ο> О, и я/2 <а<л, если < 0.

69. β = ω Yη³— 1=5 с"¹.

70. a) ο (0=% V^r^TF²e'^;,6) о (0== i*o 1 Y^ +(β/ω)²

71. Ответ зависит от того, какой смысл вкладывать в данный вопрос!. Во времени затухает быстрее первое колебание. Если же взять дяя каждого колебания его естественный масштаб времени —период T_t то за это время быстра затухает второе колебание.

72. λ = ηλο/Υ 1+(1-/2²) (λ₀/2π)² = 3,3, η' =Y\ + (2π/λ_β)² = 4,3 раза.

73. T = |/*(4π* + λ²) Axfg=OJQ с.

74. Q = Tinfln η = 5 * IO².

75. S^ I (1 +е~^Л/2)/( 1 ~е-^А/2) =2 м.

76. Q = V₂]/"71¾-¹ =¹'ЗЛО²,

77. Г=/»/ (4π* + λ²)#/£ = 0,9 с.

80. η=2Ш/лЯ*7\

81. χ =2Rifa*B*.

82. a) T = 2л j/~m/x=0,28 с; 6) η = (χ₀—Δ$4Α = 3,5 колебания, здесь A~kmgfx.

ϊ** ! hi

80. а; = ₀ ⁰ (cos — cos ωί).

CO^z — COq

4.84» Уравнения движения и их решения:

t τ, л + сф:=Ffm_t χ = (I — cos ω₀ί) Ffk_t /^τ, £+0)^ = 0, χ = α cos [ω₀ (/—x) + aj,

где (i>l = kfm, а и α — произвольные постоянные. Из условия непрерывности χ и χ в момент t=x находим искомую амплитуду:

а — (ZFjk) \ sin (ω₀ί/2)

η g _ XF₀M / 4л»\

P^e3 ~~ ρ 1 + (λ/2π)² д/ » ^aP^e3 4jimgf \ λ²/

86. ω_ρ63=!^(ω?+ω1)/2 = 5,1 . IO² рад/с.

87. a) Cd₀ = V^rCO₁O₂; б) β = | со₂ — ωχ |/2/зГ, ω = /ωιω₂ — (со₂—ωι)²/12^

88. η = (1+λ²Ζ4π²) лД=2,1.

89. A = naF₀ sin φ.

90. a) Q=V₂ γ _φ -I =0,35; 6) /4 =Jima² (ω²—ω«) tg φ

6 мДж. Здесь ο)₀ = Yy_tJm.

86. a) (P) = ; 6) _ω=(θο. <P>„_aKC=f*/4p«.

4 92 (^pWc-(P) 100

²· (Р)накс -

4.93. a) A = -n_WmN_m sin «; 6) Q=^^coa«+^У^тУ-' .

i? A sin CX

■ 4.94. 0) = 1/7^^=1,65.10^ рад/с.

95. V²+ I²LJC = Vf_n.

96. a) / = /_msin ωΛ где /_т«(/_т/C/L,'©o =IZ^^rLC; 6) S_i = CZ_mYS".

97. Л = (η² —

98. a) T=^fInYb (C₁+ C₂) =0,7 мс; б) Z_m = CZ /(C₁ +C₂)/L=8 А.

99. t/ = ^х/₂ (1 ± cos ω/) CZ₀, где знак плюс—для левого конденсатора, знак минус —для правого; ω = Y 2 JLC.

100. Z = -^ cos (f/УТС).

Kti 1 β

95. tf²C

    a) = —; б) f_rt=—arctg -^+jin. Здесь η=0, I_i 2, ...

4.102. t/o/t/m = ]/"¹

4L '

4.103. JT_c = I_m YL/C е-β' sin (ω/+α), причем tg α = ω/β; U_c (0)=I χ

*γ

C (1 +β²/ω²)

104. W_LjW_c = L/CR²=5.

105. L = Z,_X+L₂, /? = ¾+¾.

106. f = —- In η=0,5 с.

πν

⁴·^,()7· «Чг/гда--¹-¹⁸·

108. = 1 ¹ g-i—^— = 0.5¾.

ω₀ Y1 + l/(2Qp 8 Q²

108. a) ft?„ = V>£- (L+CR ')/(r + tf )2=2,0 мДж; 6) «7 = W₀c~^m = 0,10 мДж.

^ In η= 1,0 мс.

Γ ι ] ι A4_R2_C

111. a) ω = ]/ — ; 6) Q —y]/ — 1. При решении

следует учесть, что dqfdt=l —Ι', где q—заряд конденсатора, / — ток чере=* катушку, /'—ток утечкн (J^f = UfR).

111. 0^2¾ j/"^ = ¹'⁰'¹⁰²·

112. (P)=R(IZ)=If₂RIZ_rn = 20 мВт,

113. 4.115. ω=]/^—

     (P)=If₂RCUmfL = S мВт.

1

117. 4.110. ft=»

     I=^-t<r^t/VLC ; I = = ~ в момент ^ =

118. / = [cos (ω/—φ) — cos φ - tg<p=oL/fl.

/Я²+CO²L²

£/

[cos (ωί—φ)—cos φ « e ^^c], tgq) =

YR²+ If(H)Cf ~ ~ ' <&RC *

120. Ток отстает по фазе от напряжения на угол φ» определяемый урав-

нением tgy=^ .

120. Ток опережает по фазе напряжение иа угол φ=60®, определяемый уравнением tg y^VWmfRImf — 1.

121. a) U' = U_Q+U_m cos (ωί—α), где U_m = U₀/Yl + (оДС)², α =

«= arctg (o#C); 6) RC=Vrf—I/ω=22 мс.

120. /я

     4.119. / =

     См. рис. 31.

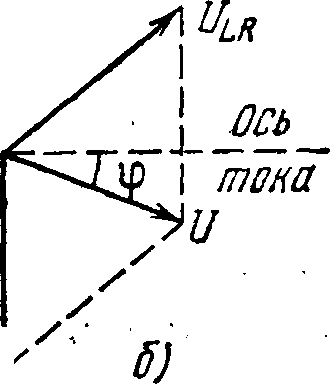
Un^

Un₀ ^тка G)

Рис. 31.

GiL-IfidC R

4.124. a) I_m=UjVR*+{(&L— IjaCf = AS А; б) tg<p =

φ= — 60° (ток опережает напряжение); я) U q = I _mfaC=0,65 кВ, = ~/m/#² + fi>²L² =0,50 кВ.

125. а) ω = /ω§ — 2β²; 6) ω = ω^/ω* — 2β², где ω^Ι/LC, β = £/2Ζ,.

126. При C = -I_r = 28 мкФ; t/_L = t/_m /1 + (ωί,/fl)² = 0,54 кВ; U_c

ω²Ι

= U_mULfR = OM κΒ.

U₁

4.127. Z = /_mcos (otf+φ), где Z_m = --^ + (ω/^С)² и tg<p=G>flC.

К

4.130. Q =

« ч iy ^ л Γ

[.128. =

С — Мз) 4.129. Q =/я² —1/₄.

LTT

4 ·

(я-I)²

, 4.131. a) ω_ΰ = ]Λ^; 6) Q=J/ ^^^ _Т -

133. I₀/I=Yl + (Q* + ^lU) (η³ —1)²/η²> соответственно 2,2 и 19.

134. t = ^lUnt₀. 2 , , _ „

R

136. V=-^J-Yv_i-1 =2 кГц.

137. Ток отстает по фазе от напряжения на φ = arccos JZ^rI — {X JZ)²

Г/2 ,

^37°, P = ^yW-Kl= 0,16 кВт.

U²

136. При R = aL — r = 0,20 кОм; Р_маКС = -^- = 0,11 кВт.

137. Увеличилось на Yn-1^:30%.

138. При Q>1 отношение Δω/ω₀^¹I₂Yn- 1/Q=0,5%·

139. P₂ = V₂ (U²-Ul-UI)/R = 30 Вт.

140. P₁ = V₂ (/²-/? —/1 R = 2,5 Вт,

141. Z=tf/j/"l + (toCtf)² = 40 Ом,

142. 1,15Ζ₀; б) I=-P--I₀^ I₁IlZ₀.

     4.135. a) I = -P- Z₀ ' /3

     См. рнс. 32.

j
Ось		К
напряжений Vo	N	<J
Ir 1lr	Il	в)

Ось

φ Напряжении \

\

L147. Z = j/~·

4 14fl /F \ (Q²UL₁₂Il dl₁₂

4.1^. + дх '

₁₅₀ ^2/

151. Δ([ = j (X₁ — X_i) cos α + — ί/₂) cos β + (Z₁ —Z₂) cos γ

/ ^егг λ

151. k = o Ь —+ — .

\ V₁ V₂ V₃ j

151. E = acos [(1 — ν/ν)ωί—kx'], где ν = ω/&

155. R²+ω² L²

     a) α/λ = 5,1 . 10 5; б) »,„ = И см/с, 3,2- 10^; в) (d£/dx)_m = 3,2 · 10"*, {dydt)_m = v(dydx)_my где ι»=0,34 км/с—скорость волны.

156. См. рис. 33.

Рис. 33.

4.157. Δφ=-~£In (1-η) ^ ^=0,3 рад.

158. г = (0114 + ^)/(*¾ + ¾).

ч ^1п (η^ο/г) _{Л ЛО} - 2nva_f,

158. а) γ = ид/; ^_{qq8 м}-_х. _б) ^_m=-

= 15 см/с.

Г .V

' Гл ⁴J

Рис. 34.

4.160. а) См. рис. 34, а. Частицы среды в точках на сплошных прямых (у=х + пХ, л = 0, 1, 2, ...) колеблются с максимальной амплитудой, на пунк­тирных же прямых—не колеблются вовсе.

б) См. рис. 34,6. Частицы среды в точках на прямых y=x + rik* ± (я it¹/₂) λ и у=х±(п± ¹U) λ колеблются соответственно вдоль этих пря« мых, перпендикулярно к ним и движутся по окружностям (здесь л = 0, 1. 2, ...). В остальных точках частицы движутся по эллипсам. 4.161. <ш) = ²/₃ш₀.

1

4.162. <Φ)==2π/²/₀( 1

ул+тг.

163. (Q) = PfVl+(ZRjhf Вт.

164. =20 мкВт.

     а) и б)—см. рис. 35; в)—см. рис. 36.

t=Q

δξ/dx

р(х)

t-T/B

Рис. 35.

4^s- dt

/-•ν

/ ν

j \ / {

—\ < p / —a >

X #

4 ^T /

О

ч у ^ .

Рис. 37.

4.165. а) Юр=»^^»²®²sin²fe*.cos²ω/; 6) w_k=¹Z^a²Q^acos⁸fej · sin² ω*. См. рис. 37.

166. Ямакс=5 мм; третьему оберюну.

167. ^- = Т/"Й1Н)=1,4.

Vi Г Tli (1 + Лг)

Х' 1 д у¹

166. Увеличится в η = ■ ^ ^ ^—=2 раза·

167. ε>=2/ν = 0,34 км/с.

ϋ г

166. а) х_п = ~ (2ra-fl), шесть колебаний; б) ν,,=-^ (л+1), тоже

шесть колебаний. Здесь л = 0, 1, 2, ... 2 и -4-1 £

166. v,j=——⁼⁼⁼³»8(2/г+1) кГц; четыре колебания с часто­тами 26,6, 34,2, 41,8 н 49,4 кГц.

167. а) Г_макс=У₄то)²а*_акс; б) <Г> = V₈^aJ_{1 акс},

168. Ψ = ^UnSpaPa²Ik.

169. v=2v₀y«/(y²— w²)^2v₀tt/P=l,0 Гц.

170. и = (V^rI + (v/vo)²-1)^^-=0,5 м/с·

V₀ ZVo

166. ω = (V^rI + (Δν/Vo)² -1) = 34 рад/с.

167. V=V₀ZF^rI +2w*/i> = 1,35 кГц.

168. а) ν = ν₀/(1 ~η²)=5 кГц; б) г = I V1+^=0,32 км,

169. Уменьшается на 2u/(v + и)=2,0%,

170. ν=2v₀uj(v+ и) =0,60 Гц.

171. γ=¹"/^^ = 6-10-3 м-1.

2(Г₂ — T₁)

166. a) L^f = L—20γ* Ig е = 50 дБ; б) х = 0,30 км.

167. a) L=L₀+201g(r₀/r) = 36 дБ; б) г >0,63 км· ,

168. β = (1ηΛ)/τ = 0,07 с

169. а) Рассмотрим движение плоского элемента среды толщиной dx с единичной площадью поперечного сечения. Согласно второму закону Ньютона

pdx- t,= — dp, где dp—приращение давления на длине dx. Учитывая, что

ζ=ν² (д^/дх²)—волновое уравнение, перепишем предыдущее равенство в виде

d²l·

Проинтегрировав это уравнение, получим

_Л dl·

Ap=-QV² —[-const.

В отсутствие деформации (волны) избыточное давление Δρ=0. Отсюда Const=O.

166. <Φ>=π£²(Δρ)^/2ρνλ=11 мВт.

167. a) (Ap)_m = VpvPftnr² = B Па, (Ap)_m/p=5 .104; б) а=(Лр)_т/2лур*« Ss 3 мкм, σ/λ=5·10~^β.

168. P =Anr²C^2yrI₀- IO^l= 1,4 Вт, где L в белах.

169. Δλ=(ΐ/Τ^ε~—1) c/v= —50 м.

170. Ijc In Ce₁Ze₂).

4.191» ///_CM = a/2nvee₀ = 2.

192. N=^r V^rVf¹O cos (ckt), где с—скорость волны в вакууме.

193. a) U=C_zE_m Vl^J^ cos kx = — 0,30e_z; б) Н==е*Е_ш/¾¾ χ X cos (ckt₀ — &x) = 0,18e_z. Здесь е_г — орт оси z_y H в А'м.

194. $_инд = /£_ш [cos ωί—cos (ωί — ωΖ/с)] = 25 cos (ω/ + π/3) мВ, Здесь Ы/с=л/ 3.

196. (S) = V₂^oC²Em/⁰*.

197. а) /_см = π ^e₀VE_m = 0,20 мА/м²; б) (5) = ν₂ε₀^ = 3,3 мВт/м*.

198. Здесь *>7\ где Г —период колебаний, поэтому W = V₂ Κεε^/μ^ χ X EhnRH = Ъ кДж.

199. B = B_r7z sinfex- sin ωί, где B_m 1 Е_ш, причем B_m = E_mIc.

200. S_x = *иг₀сЕ% sin 2/гх · sin 2ωί, <S_A.)=0.

201. r_M/r₃ = V8^oO)²/^2 = 5,0. 10-АЗ.

202. ^₉/^_Μ = ν₈ε₀μοω²^² = 5,0. 10^2.

204. Ф₅=/^гЯ.

205. 5 = /²/ίη/Μ7/4π²ε₀Γ².

207. Слева.

208. Φ = ί/7.

209. (Φ) =V₂^oZo cos φ.

4.211. Электриче;кий дипольный момент системы ρ = er. = (elm) Mr_r^

где Λί —масса системы, г_с — радиус-вектор ее центра инерции. Так как мощ-

.«2 "2 "

ность излучения ρ ^ г_с, а в нашем случае г^ —0, то и P = 0. ⁴·²¹²· ^=¾-^=⁵-¹⁰"^{5 Βτ}·

- J_ _ / ^{2,5 (}

'""!Г" \ 1,6.

ϊ 2 ί qe² γ 1 ne*q²

214. ν, о ч a « ·

(4лг₀)³ Зс³тЧ>0³

214. АГ /Г = V₃^BIEqcW = 2 · 10-м.

215. Г = T₀e~^at, где a = ^lI^B²Jnt₀Pm*. Через

, 2,5 с для электрона,

L

Ю¹⁰ с = 0,5 · IO³ лет для протона.

214. S_t/S₂ = tg² (td//c) = 3.

215. а) Пусть t—момент времени, когда частица находится в определен-· ной точке у окружности, a f — момент, когда информация об этом доходит до точки Р. Обозначив наблюдаемые значения ^-координаты в точке P че­рез у' (см. рис. 4.40), запишем

С

Искомое ускорение найдем двукратным дифференцированием у' по f: dy' _ dy dy dt dry' __ dt d (dy'\ ν² v/c — y;R

df dt' dt dt' dt* dt' dt \dt'j R (i —_Vy!cR)% где учтено, что χ = R sin at, у = Rcosat и a = vJR.

б) Плотность потока энергии электромагнитного излучения S пропорцио­нальна квадрату «/-проекции наблюдаемого ускорения частицы. Отсюда SifS₂ = (\ ^vfcff(X-Vfc)*.

214. <Р> =V₃Jtr²S₀.

215. (w)=s/_sP₀fnr*c.

216. Р = ¹/_вр²(й*/пе₀сК

217. (P)/(S) = (e²fm)yifin.

4 223 (Ρ)!(S) — ^ (e²fm)² ω*

4.224. ^ = ЗР/1бясурМ_с^0,6 мкм.

1. а) 3 и 9 мВт; б) O = V₂ (V_i + K₂) Ф_э/Л = 1,6 лм, где Л = 1,6 мВт/лм, ViH V₂-значения относительной с ектральной чувствительности глаза для данных длин волн.

2. Em = Ι^μο/εο ΛΦ/2πΛ²Κ_λ, отсюда E_m = I_tI В/м, #_m = 3,0 мА/м. Здесь А = 1,6 мВт/лм, V χ —относительная спектральная чувствительность глаза для данной длины волны.

3. a) (E)=V₂^ о; б) (E) =^{l it}^ ^-50 лк.

4. M = ²f₃nL₀.

5. a) O = JtLAS sin² θ; б) Λί=πΔ.

6. h^R, E = LSfAR² = AO лк.

7. / = /₀/cos³ft, Φ = nl₀R²fh² = Ъ · IO² лм.

8. Емакс = (9/16л pESfR² = 0>2\ лк, на расстоянии RfV^ от по­толка.

9. E =^^r ziL.

10. E = nL.

11. M = £₀ (1 + h²fR²) = 7 · IO² лм/м².

12. E₀ = nLR²fh² = 25 лк.

13. е' =е—2 (en) п.

14. Пусть M₁, п₂, п₃ — орты нормалей к плоскостям данных зеркал, а е₀, ®ί» ^е2» е₃ —орты первичного луча и лучей, отраженных от первого, второго и третьего зеркал. Тогда (см. ответ предыдущей задачи):

C₁ = C_ft-2 (C₀Ii₁) щ, е₂ = C₁ — 2 (C₁Ii₂) п₂, е₃ = е₂ —2 (е₂п₃) п₃.

Сложив почленно левые и правые части этих выражений, нетрудно показать» что е₃=—е₀.

15. fti = arctgrt = 53⁰.

16. _Л1/Л₂=1)Л^Л = 1,25.

17. x = [l-V(i-sin² $)f(n² - sin² fl)] d. sin θ = 3,1 см.

18. h' = (iHn² cos³ Ъ)!(η² — ύη² ϋ)^3/2.

21. 0 = 83°.

22. От 37 до 58^э.

23. α = 8,7°.

2 sin (θ/2)

21. Δα =—.. ^{ν 1} ' Δ/ΐ = 0,44*.

V 1 — η² sin² (θ/2)

27. a) / = /β/(1 — β²) = 10 см; 6) /-/βιβ₂/(β₂-β^ = 2,5 см.

28. /' = p/o/W-5)2 = 2,0-103 кд.

5.29. Пусть <$ —точечный источник света и S'— его изображение (рис. 38), По принципу Ферма оптические длины всех лучей, вышедших из S и собрав* шихся в S', одинаковы. Проведем окружности из центров S и S^f радиусамя SO и S'M. Тогда оптические пути (DM) и (OB) должны быть равны:

л -DAi = л'· OB. (*)

Но для параксиальных лучей DM ¢=¾ АО + ОС, где AO^h²/(—2s) и CC да* e^h'^fiR. Кроме того, OB-=OC-ВС ¢=¾¾'³pR — h'²/2s'. Подставив эти выра-ι жения в (*) и имея в виду, что ft' ¢=¾ ft, получим n'js' —- /г/s = (/г' — n)lR·

Рис. 38«

^5Ж '=IqM¹-j^HSu?)· ^=^(,-1)/(. + 1).

31. 6,3 см.

32. а) β = 1—<*(л—1)/лД= — 0,20; б) E = nnW²L/4d*=42 лк. Б.ЗЗ.'а) Ф== Ф₀ (л —л₀)/(л —1) = 2,0 дп, /' = — /=л₀/Ф = 85 см; б) Φ =э

= Va^jDoprt-«о— 1)/(л — 1) = 6,7 дп, /=1/Ф^ 15 см. /' = л₀/Ф«*20 см. Здесь л и я₀—показатели преломления стекла и воды.

35. Δχ^Δ//2/(/-/)2== 0,5 мм.

36. а) /=[/² — (Δ/)²]/4/ = 20 см; б) /=/Уц/(\ +/ΐ[)² = 20 см.

37. ft = Yh^rJf=3,0 мм.

38. E = (1—a) TiLD^%/4p = 15 лк.

39. а) Не зависит от D; б) пропорциональна D².

40. f — n_QR/2 (/г_х — /г₂) = 35 см, где л₀—показатель преломления воды.

41. /=#/2 (2л—1) = 10 см.

42. а) Справа от последней линзы на расстоянии 3,3 см от нее; б) I =г 17 см.

43. а) 50 и 5 см; б) отодвинуть на 0,5 см.

44. T=Djd.

45. =0,6'.

46. Г' = (Г + 1) ———^_t-1=3,1, где л₀—показатель преломления

^rtO \^п — *)

воды.

35. Г ^ Ztyd₀ = 20.

36. Г = 60.

37. а) Г=2а/₀/<2₀= 15, где /₀ —расстояние наилучшего видения (25 см); б) r^2a/₀/d₀.

5.50. Главные плоскости совпадают с центром линзы. Фокусные расстоя* ния в воздухе и воде: /= — 1 /ф = —11 см, = л₀/Ф = + 15 см. Здесь Φ S= (2я — по — 1)/R_t где η и п₀ — показатели преломления стекла и воды. Узло­вые точки совпадают и расположены в воде на расстоянии х=/'-|-/=3,7 см от линзы.

5.51. См. рис. 39.

H H^t

•		4		/ Fr
i	.		f 4

а)

H

H^f

4	k	1 A	\ I
		! F	F'\	F
		I I	\
1	f	I I \	' !

б)

Рис. 39.

54. а) Оптическаи сила системы Φ = Φι+Φ₂ — όΦχΦ₂= +4 дп, фокусное расстояние равно 25 см. Обе главные плоскости расположены перед собираю­щей линзой: передняя — на расстоянии 10 см ст собирающей линзы, задняя — на расстоянии 10 см от рассеивающей линзы (х=^Ф₂/Ф и χ' = — <2Φι/Φ); б) d = 5 см; около ⁴/₃.

55. Оптическая сила данной линзы Ф = Ф₁-+Ф₂—(d[n) Ф_гФ₂, χ=■ =э ^Ф₂/лФ=5,0 см, χ' =—άΦ₁/ηΦ=2_>5 см, т. е. обе главные плоскости рас* положены вне линзы со стороны ее выпуклой поверхности.

f f

54. /=2—τ^β—-τ-. Линзу надо поместить в передней главной плоскости

/IT/2""

системы, т. е. на расстоянии *=fW/(fi+/₂ — d) ^от первой линзы.

54. Ф = 2Ф' —2Ф'²///г₀=3,0 дп, где Ф' = (2л — n_Q — 1)/Я, η и п₀ — пока­затели преломления стекла и воды.

55. a) d = nAR/(n —1)=4,5 см; б) if = 3,0 см.

56. а) Φ= d(n— 1)²/лД²;>0, главные плоскости лежат со стороны вы­пуклой поверхности иа расстоянии d Друг от друга, причем передняя главная плоскость удалена от выпуклой поверхности линзы на расстояние R/(n— 1); б) O = (IfR₂-IfR₁) (п — 1)/п < 0; обе главные плоскости проходят через общий центр кривизны поверхностей линзы.

57. ά = 4₂η (R_i +R₂)f(n —1)=9.0 см, T = R₁ZR₂=M.

58. Φ = 2 (л²—1)//г²Л = 37 дп.

5.63. р = 3· 10? ы; gradrt = 1,6-10^7 м-*.

65. 1,9а.

66. Представим k-e колебание в комплексном виде

ь — ee'"^+« - _

где а* = ае^г^ ^—— комплексная амплитуда. Тогда комплексная амплитуда результирующего колебания

k = \

После умножения А* иа комплексно сопряженную величину и извлечения квадратного корня получим действительную амплитуду

- cos Mp sin А = а I/ —_; = а—г

γ 1 — COS φ SIl

sin (φ/2)

67. a) cos φ = (£ — ф/2л) Xjd_f к = O_t it 1, ±2,...; б) φ=π/2, d/X => = 6+¹/^ £ = 0, 1, 2, ...

68. Δφ = 2π [£ — (d/X) sin (Ш + α)], где £ = 0, ±1, ±2, ...

69. λ = 2ΑχΑΗβ (η — 1) = 0,6 мкм.

5.71. a) Ax = X (b + r)ftar = 1,1 мм, 9 максимумов; б) сдвиг картины δχ = = (b/r)6l = 13 мм; в) картина будет еще достаточно отчетлива, если δχ^Δχ/2, отсюда Ь_тК(. = (\+г/Ь)Х/Аа = АЪ мкм. £ 5.72. λ = 2αΔχ = 0,64 мкм.

73. а) Ах = Х[/а = 0ЛЪ мм, 13 максимумов; б) полосы будут наблюдаться еще достаточно отчетливо, если δχ=<:Δχ/2, где δχ—сдвиг интерференционных картин от крайних элементов щели, отсюда б_макс =λ/²/2α& = 37 мкм.

74. Х = 2а0 (η — I) Δχ/(α-f-fr) = 0,6 мкм.

75. Δχ ^ λ/26 (η —η') = 0,20 мм.

76. Полосы сместятся в сторону перекрытой щели иа расстояние Ax = hi (п— l)/d = 2,0 мм.

77. п' = п + NXll =1,000377.

78. а) Пусть векторы Е, E' и Е* соответствуют падающей, отраженной и проходящей волнам. Из непрерывности тангенциальной составляющей на границе раздела следует, что

(1)

Плотность потока энергии S = [E Η], а так как H V\Wo = E V^o, или H ~пЕ,

где η = Vг—показатель преломления, то S^nE² и по закону сохранения энергии

ⁿi^Ei = ⁿi^E'x+ⁿ2^EC- (2)

Исключив Е'_х из (1) и (2), получим

E^E_xH_lKn_l +η ₂). (3)

Отсюда видио, что знаки E_x и E_t совпадают, т. е. на границе раздела коле­бания световых векторов соответствующих волн происходят всегда синфазио. б) Из (!) и (3) следует, что

Εχ = E_x (/I₁ — п₂)1(п_г + /½),

т. е. при > /г_г знаки Е% и E_x противоположны —на границе раздела проис­ходит скачок фазы отраженной волны иа π. Если же то скачка фазы иет.

73. d = ¹I_4tX (I +2k)/Vn² — sin² A₁ = O_iH (1 +2k) мкм, где £ = 0, 1, 2, ...

74. d_MHH = 0,65 мкм.

75. d = ¹UX(\+2k)/Vn_t где £ = 0, 1, 2, ...

_ _ПЛ „ Vn²-sin² θ

73. d = X ■ . _ой =Io мкм.

sin 2ϋ · oft

(Λ/φ/2)

φ

d(r}-r I). ⁵·⁸³' 4nl²(i-k) '

5.84. Δχ= ^λεο8θί

2α |/~/г³ — sin² Oi'

85. a) Q = ¹I₂Xlnte = V; 6) Δλ/λ «d Δλ:// = 0,014.

86. Ar^¹ItXRlr.

87. /-' = ]/> —2ΑΔΑ = 1,5 мм.

88. г = Vrl + (ft — ¹I₂) XR = 3,8 мм, где ft = 6.

89. X = ¹I₄ (d\ — dl)/R (k₂ — k_x) = 0,50 мкм, где kf и номера темных колец.

90. Ф = 2 (η— I) (2ft — I) λ/ί/²=2,4 дп, где ft — номер светлого кольца.

91. а) г = V2kX (η — I)/ф = 3,5 мм, где Zfe = IO; б) r' = r/|/7z7=3,0 мм, где /г_а—показатель преломления воды.

92. г = V¹I₂ (I +2k) XRln₂ = 1,3 мм, где ft = 5.

93. ^ = ¹I₂X₁I(X₂-X₁)=IAO.

94. Условие перехода от одной четкой картины к следующей:

(ft + I) λί = £λ₂,

где ft — некоторое целое число. Соответствующее перемещение Δ/г зеркала опре­деляется уравнением 2Ah=kX₂. Из этих двух уравнений получим

^{М =} 2W = ⁰'^{3 ММ}·

85. а) Условие максимумов: 2rfcosd = ^; отсюда следует, что с ростом угла θ* т. е. радиуса колец (см. рис. 5.18), порядок интерференции k убывает, б) Взяв дифференциал от обеих частёй предыдущего уравнения и имея в виду, что при переходе от одного максимума к следующему k изменяется на еди­ницу, получим δθ = ¹Z^fd sin ft; отсюда видно, что угловая ширина полос уменьшается с ростом угла ft, т. е. с уменьшением порядка интерференции.

86. а) &макс ~2^/λ = 1,0 · 10*; б) AX = Xfk = X²/2d = 5 пм,

OO

5.97. I₀ =

^ I (г) г dr.

bNX

о

5.98. b = ar*f(kXa—г²) = 2,0 м. . 5.99. λ = (rl — rl) (a + b)f2ab = 0,60 мкм.

100. а) / =¾ 4/₀, /^2/₀; б)

101. а) /^0; б) / ^ 1^2.

102. а) /ι«»·/ιβ^ο. ^ = VJe. Z₃ = Vie^. h = / ^ (1—<φ/2π)²/₀;

б) /₆^^2δ/ιβ'ο> /?^⁴ⁱ7ie'o, /g = /₆> /^(1+φ/2π)²/₀. Здесь φ— угол, закрываемый экраном.

100. a) А = λ (ft + ³/₈)/(я—1) = 1,2 (ft + ³/₈) мкм; б) A= 1,2 (ft+%) мкм;

в) A= 1,2ft или l,2(ft + ³/₄) мкм. Здесь ft = 0, I, 2, ...

100. A=X(ft + ³/₄)/(rt— ^гД^е ^ = ²» ■··; ^б) /макс^в/в-

101. Амин — λ (ft + ⁶/_§)/(rt —1)-2,5 мкм, где k = 2. Τίθ6Γ"7Ξ=^λ^/(^--/)==0,90^ мм, где ft=l, 3, 5, ...

107. Ь' = ЬЩ²= 1,0 м.

108. а) у' = ybja = 9 мм; б) А_мин ^abXjD (α + 6) = 0,10 мм.

109. f=abfta + b) = 0,Q м. Это значение соответствует главному фокусу, помимо которого существуют и другие.

110. a) h = 0,60 (2k+ \) мкм; б) Л = 0,30 (2k +1) мкм. Здесь fe = 0, 1, 2,...

111. а) /макс/^мин^ 1.7; б) Х = 2 (Ax)²Jb (v₂ —1^ = 0,6 мкм, где v% _и V₂—соответствующие значения параметра на спирали Корню.

112. /_сер/Лср^2,6.

113. λ = (ΔΛ)²/26 (и₂— C₁)²=0,55 мкм, где н V₂ — соответствующие зна« чения параметра на спирали Корню.

114. h^X(k + 3U)!(n— 1), где fe = 0, 1, 2, ...

115. /2//^1,9.

116. 2,8/(,.

117. /t:/₂:/₃c=«l :4:7,

118. /r=5/„.

119. со (sin² α)/α², где α = (π/?/λ) sin Α; έ>5ίηΑ = &λ, £ = 1, 2, 3, ...

120. Условие максимума приводит к трансцендентному уравнению tga = е= а, где а = (nblX) sin А. Решение этого уравнения (графически или подбором) дает следующие значения корней: α_λ = 1,43π, α₂ = 2,46π, α₃ = 3,47π. Отсюда b sin A₁ = 1,43λ, b sin A₂ = 2,46λ, b sin A₃ = 3,47λ.

121. b (sin A— sin A₀) = kX\ для k=+\ и £= — 1 углы А равны.соот­ветственно 33° и 27°.

122. a) AA = arcsin (η sin Θ) —Θ=7,9°; б) из условня b (sin Aj- η sin 6) = = ±λ получим ΔΑ=Α₊|— Α_ϊ = 7,3°.

123. λ«*(α²—α§) <2/2fc = 0,6 мкм,

125. 55°.

126. <i = 2,8 мкм.

127. X = (d sin ΔΑ)/Κ 5—4cos ΔΑ = 0,54 мкм.

128. а) 45°; б) 64°. *

129. x = 2JR/(«— 1) Y(djVf— 1 = 8 см.

130. Из условия d [п sin Θ — sin (6 + Aj_fe)] = kX получим A₀=-Ie_iS*, θ_+ί = 0°; й„акс=+6, Α₊₆=+78,5^β. См. рис. 40.

131. h_k = X(k—^lk)l(n— 1), где fe=l, 2, α siηΑί=λ/2.

132. V = XvffAx= 1,5 км/с.

г d

Рис. 41.

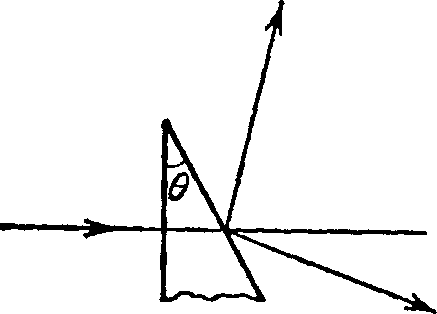
^AiOKC &

Рис. 40.

к=0

L

5.133. Каждая звезда дает в фокальной плоскости объектива свою дифрак­ционную картину, причем их нулевые максимумы отстоят друг от друга на угол ψ (рис. 41). При уменьшении расстояния d угол А между соседними максимумами в каждой дифракционной картине будет увеличиваться, н когда А

станет равным 2ψ, наступит первое ухудшение видимости: максимумы одной системы полос совпадут с минимумами другой. Таким образом, из условия 0=21]? и формулы sin O¹ = λ/ί/ получим if>^X/2<i = 0,06*.

134. a) D = kfdV 1 — (kXfdf = 6,5 угл.мин/нм, где k = 2; б) D =

^kfdy^rX-(kXfd — sin A₀)²== 13 угл.мин/нм, где £=4.

134. d$fdX = (tg$)fX.

135. ΔΑ == 2XjNd Y1 — (kX/d)² = 1 Г.

139. θ = 46°.

140. а) В четвертом; б) δλ_ΜΗΗ^λ²//=7 пм·

141. a) <2 = 0,05 мм; б) 1 = 6 см.

142. а) 6 и 12 мкм; б) в первом порядке нет, во втором да.

143. Согласно критерию Рэлея максимум линии с длиной волны λ должен совпадать с первым минимумом линии λ + δλ. Запишем оба условия для угла наименьшего отклонения через оптические разности хода крайних лучей (см. рис. 5.28):

bn — (DC+CE) = 0, Ь (η+δη) — (DC+CE)=X + SX.

Отсюда ЬЬп «й λ. Дальнейшее очевидно.

139. a) XfbX=2bBfX^z\ соответственно 1,2- 10* и 0,35-10⁴; б) 1,0 см.

140. Около 20 см.

141. R = 7-IO⁴, Ау_ишя&4см.

142. Около 50 м.

143. Пусть Δψ и Aif' — минимальные угловые расстояния, разрешаемые соответственно объективом трубы и глазом (Δψ=1,22λ/0, Δψ' = 1,22 Xfd₀)* Тогда искомое увелH¹IeHne трубы Г_мин = Δψ'/Δψ = Djd₀=XZ.

144. <i_MlTH=0,61 λ/sin α = 1,4 мкм.

145. Пусть d_MWH—наименьшее разрешаемое расстояние для объектива микроскопа, Δψ—угол, под которым виден объект с расстояния наилучшего видения I₀ (25 см), и Αψ—минимальное угловое расстояние, разрешаемое глазом (Δ·ψ'= 1,22 Xfd₀). Тогда искомое увеличение микроскопа Г_мии = Δ-ψ'/Αψ = с= 2 (Infd₀) sin α = 30.

146. 26, 60, 84, 107 и 134®.

147. α = 0,28 нм, 6=0,41 нм.

148. Пусть α, β и γ —углы между направлением на дифракционный максимум и направлениями решетки вдоль периодов a, b и с соответственно. Тогда значения этих углов определятся из условий: а( 1—cos α) = k_xX, 6 cos β =□ = β₂λ и с cos γ=Имея в виду, что cos² α + cos² β + cos² у = 1, получим

- 2¾fa

2 ³ ί т

139. X = —у — sina=244 пм, где k=2> т—масса молекулы NaCl·

140. d= _{2 5ΐη}^λ(_α/2) Vkl + 4—2k_tk₂ cos (α/2) =0,28 нм, где k_± и

-порядки отражения.

139. r = /tg2a = 3,5 см, где а—угол скольжения, определяемый уело·» вием 2dsina=kk·

140. /₀/4,

- 5Л58. *) /<,; б) 2Z₀.

159. £ = πΦ₀/ω=0,6 мДж.

160. η = V₂ (cos φ)² ^-^ = 0,12.

161. /₀//= , ². ^60.

τ³ cos⁴ φ

159. /_пол//ест = Я/(1--Р) = 0,3.

160. Ρ = (η —1)/(1-η cos 2φ) = 0,8.

161. а) Представим естественный свет в виде двух взаимно перпендику-— лярных составляющих с интенсивностями I₀. Пусть каждый поляризатор про­пускает в своей плоскости долю а_х света с плоскостью колебаний, параллелыюй плоскости поляризатора, и долю O₂ — в перпендикулярной плоскости- Тогда при параллельных и перпендикулярных плоскостях поляризаторев системы интенсивность прошедшего через нее света будет равна соответственно

¹H=^aI¹Q+ «Уо» ⁷X = ^α1^α2^;0 +Ct₂Ct₁Z₀,

причем по условию

С другой стороны, степень поляризации, создаваемая каждым поляриза­тором в отдельности,

Po = («ι—α₂)/(αι+0¾). Исключив и O₂ из этих формул, получим

Po = V {ц-~\ )/(η + 1) = 0,905, б) P = V^rI — 1/η3 =0,995.

159. Относительные изменения интенсивностей обоих пучков в случаях < А и В равны

(М/1)_А = 4 ctg (φ/2). δφ, (MfI)₈ = 4 tg (φ/2) · δφ.

Отсюда η = (ΔΖ/Ζ)^/(ΔΖ/Ζ)_β = ctg² (φ/2), φ= 11,5°.

159. 90°.

160. a) ρ = ^l/a (л² — 1 )²/(η² + I )² = 0,074; 6) =

= 0,080. Здесь η~ показатель преломления стекла.

159. Z = Z₀ (I — ρ)//ι = 0,72Ζ₀, где η — показатель преломления воды.

160. р = [(л^а—1)/(л^а + 1)] sin*φ = 0,038, где /г — показатель преломления воды.

161. P₁ = P₃=I, P₂ — — = 0,087, =0,17.

I—ρ 1 — 2р (1 — р)

159. а) В этом случае коэффициент отражения от каждой поверхности пластинки ρ = (/ζ² — 1 ψ!(ti² + 1 )², поэтому

Z₄ = Z₀ (1 -ρ)²= 16Ζ₀Λ«/(1 +/г²)² = 0,725/₀;

П ι —(1—р')^а (1+П²)⁴—16л4 _Λ1β , _

^б> 1+(1-р')^{2 =} (1+/ΖΨ+16/Ζ^{4 ГДе} P-коэффициент ,отра-

жени я той составляющей света, световой вектор которой колеблется перпенди­кулярно к плоскости падения.

159. a) Ρ = (ΐ—α^47ν)/(ΐ+α^4Λ0, где а=2/г/(1 + /г²), л—показатель пре­ломления стекла; б) соответственно 0,16, 0,31, 0,67 и 0,92.

5.173. а) р = (я—1)²/(л+ 1)² = 0,040; б) ΔΦ/Φ = 1 — (1 — p)^2;v = 0,34, где N — число линз.

175. а) 0,83; б? 0,044.

176. См. рис. 42, где о и е—обыкновенный и необыкновенный лучи#

175. δ ^ 11°.

176. Для правой системы координат:

     1. круговая, против часовой стрелки, если смотреть навстречу волне;

     2. эллиптическая, по часовой стрелке, если смотреть навстречу волне; большая ось эллипса совпадает с прямой у = х\

     3. плоская поляризация, вдоль прямой у = —х.

177. а) 0,490 мм; б) 0,475 мм.

178. λ = 4^Δη/(2£+1); 0,58, 0,55 и 0,51 мкм соответственно при δ= 15, 16 и 17.

179. Четыре.

180. 0,69 и 0,43 мкм.

181. d = (fc — ν₂)λι/Δ/ζ = 0,25 мм, где £=4.

182. An = λ/ΘΔχ = 0,009.

183. Обозначим интенсивность прошедшего света при скрещенHbnt поля­роидах а при параллельных — /ц, тогда:

/^ = 1/2/0 ^{sin2 2<}Р ' ^sin2 (^δ/²)»

/ = i/₂/₀ [1 — sin² 2<р - sin² (δ/2)]·

Условия максимума и минимума:

Поляроиды	^макс	[ ^мин ;
J-	Δ = (fc+V2) λ, φ = π/4	Δ=&λ, φ — любое
Il	Δ = &λ, φ —любое	•Δ = (fc +V2) λ> φ = π/4

Здесь Δ—оптическая разность хода обыкновенного и необыкновенного лучей, £ = 0, 1, 2, ...

^! "'5.Ϊ87. а) Если свет правополяризованный по кругу (для наблюдателя), то за пластинкрц в четверть волны он становится линейно поляризованным, причем направление колебаний светового вектора составляет угол +45° с осью кристалла OO' (рис. 43, а); для левополяризованного света этот угол будет равен —45° (рис. 43, б).

б) Если при вращении поляроида (расположенного за пластинкой) при любом положении пластинки интенсивность прошедшего света не меняется—свет есте­ственный, если меняется и падает до нуля, то свет поляризован по кругу; е£ли

О

Рис. 43,

меняется, но не падает до нуля, то свет—смесь естественного и поляризован·· ного по кругу.

188. a) Δχ = ¹I₂X (п_е — п₀} 0, б) d (п'₀~п'_е) = — 2 (п_е — п₀) θδχ < 0.

189. Δ/ι=αλ/π = 0,71 .10~⁴, где а — постоянная вращения.

190. а = π/Δχ tg 6=21 угл.град/мм, I (χ) ~ cos² (πχ/Δχ), где χ—расстоя* нне от максимума.

191. ^MHH = (IZ^a) arcsin Y^t] = 3,0 мм.

192. 8,7 мм.

193. [а] =72 угл.град/(дм · г/см³).

194. а) Е_мин= 1/)/457= 10,6 кВ/см; б) 2,2-108 прерываний в секунду.

195. А/г=2сЯК/о>, где с—скорость света в вакууме*

196. K = V₂ (<Pi—ф₂)//Я = 0,015 угл. мин/А.

197. Если смотреть навстречу вышедшему лучу и положительное направ­ление отсчитывать по часовой стрелке, то φ = (a—VNH)ll_t где N — число про* хождений луча через вещество (на рис. 5.35 число N = S).

198. Hмин = π/4Vl = 4,0 кА/м, где V—постоянная Верде. Направление, в котором пропускается свет, изменится на противоположное.

199. ί=/η«ι)ο/λ/ = 12 ч. Несмотря на чрезвычайную малость этого эффекта, его наблюдали как для видимого света, так и для сантиметровых волн.

200. а) α=6Ε₀/^ω² = 5 · 10~i® см, где Е₀=|/~2//8₀с, ο=αω = 1,7 см/с; б) /у/ч = 2,9 . IO"¹¹.

201. а) ε=1—/гое²/8₀тш², v = cY\ + (n^²lAn4^)X².

202. Но = (4π²ν²/ηε₀/6²) (1— я²) = 2,4 . IO⁷ см~з.

203. /г —1 = — п₀е²Х²18л²готс²= —5,4 · 10~⁷, где щ — концентрация элект* ронов в углероде.

204. а) x = a cos (ω/+φ), где α и φ определяются формулами

а

Y (ω§ —ω²)²+4β²ω² Здесь β = γ/2^ί, = т — масса электрона, б) (P)=

2

ω?

ω

_ т / g£p γ 4β I т )

(Ρ) макс

при ω = ω₀.

eEolm 2βω

tgq>

(0)5 — ω²)²+4β²ω² »

188. Запишем уравнение волны в форме A = Α₀ε^1(ω*где &=2π/λ. Если η' = η + ικ, то ft = (2π/λ₀) η' и

или в вещественной форме

А = Л₀е^х'* cos (ω/—ft'*),

т. е. свет распространяется в виде плоской волны, амплитуда которой зависит от χ. При κ<0 амплитуда убывает (затухание волны за счет поглощения). Если п' = Ы, то

A = A₀^^x cos ωΛ

Это стоячая волна с экспоненциально убывающей (при κ<0) амплитудой. В этом случае свет испытывает полное внутреннее отражение в среде (без поглощения).

188. п₀ = 4пЧ₀тс*/еЧ|=2,0 · 10® см"*

208. а) « = ³/₂с>; б) u=2v; в) U=¹Z_sV.

209. ε=1+Λ/ω²> где А —постоянная.

210. V = Cja= 1,83-IO⁸ м/с, и = [1 + (λ/η) (dn/άλ)] с/п= 1,70· 108 м/с.

211. Достаточно провести рассуждение для трех гармонических состав­ляющих волнового импульса (проще всего с помощью графика).

' 5.212. I = Iz₂I₀Z-*¹ sin² φ, где φ = VlH.

213. а) / = /о(1 —р)²(1 + р² + р⁴+ ...) = /₀(1 —р)²/(1 —P²); б) I =

«=/₀(1—ρ)²σ(1+σ²ρ²+σ4ρ4+...) = /^(1-р)а/(1—_a2p2)_{f где а}=ехр(—raf)·

213. _к ^ ^lnJ^r"У =0,35 см-*.

α₂ — "ι

1 Π—ρ)^2;ν

213. X=-Tr_rIn ^ ^—=0,034 см"».

IN X

213. т=(1 —р)² exp [-¹I₂ (^i+ ^2) Ih

214. / = Z₀(I-P)² ^^ .

215. Δλ = 2λ₀Κ(1πη)/α£ί.

216. Z=^(l-p)²e-*<*-«\

217. Уменьшится в exp (μ£ί)=0,6 · IO² раа.

218. d = 0,3 мм.

219. d = (ln 2)/μ= 8 мм.

220. N = (In η)/1π 2 = 5,6.

221. c=2lz (n₂ —/^) = 3,0- IO⁸ м/с.

222. Прежде всего отметим, что при о<с время течет практически одинаково в системах отсчета, связанных как с источником, так и с приемни­ком. Представим себе* что источник испускает короткие импульсы с интерва­лами T₀. Тогда в системе отсчета, связанной с приемником, расстояние между двумя последовательными импульсами вдоль линии наблюдения λ = CT¹₀- O_rT_0t где лучевая скорость источника (i>_r=t>cos ф). Частота принимаемых импульсов v=c/X=v₀/(\ — v_r/c)_t где V₀=I/T₀. Отсюда (ν—v₀)/v₀=(νJс) cos <h

223. Δλ= —XVZTZmc* cos O= —26 им.

224. Γ = 4π/?λ/ίδλ=25 сут, где Я — радиус Солнца.

225. d = (Δλ/λ),_η<ττ/π = 3·10⁷ км, ™ = (Δλ/λ)^<:³τ/2πγ = 2,9. 10²° кг, где γ —гравитационная постоянная.

226. ω = ω₀(1+β)/(1—β), где р = о)^о)₀(1+2К/с).

227. υ — ¹J^KAv ^ 900 км/ч.

228. После подстановки в равенство (dt—kx^w't' — k'x' величин f и χ''· (из преобразований Лоренца) получим

ω = ω' (1 + βί/^Γ^β², k = k' (1 + βί/ΖΤ^β², где β= V/с. Здесь учтено, что =

213. Из формулы ω' = ω γ₍\ _β)/(1 +β) получим β = ^ = 0,26·

214. v = c I =7,1 . IO⁴ км/с.

215. ω = ω₀ Υ-3/7.

216. Δλ = λΤ//η₀^² = 0,70 нм, где m₀ — масса атома.

217. а) ы = щ!У 1 — β²=5,0 · IO¹O рад/с; б) W = W₀Zi^^2-=US-IOio рад/с. Здесь β =

218. Заряд электрона вместе с положительным индуцированным в металле зарядом образует диполь. В системе отсчета, связанной с электроном, электри­ческий момент диполя меняется с периодом T' = d'/v, где d^r = d Yl —(ν]с)². Соответствующая «собственная» частота V = vfd^r. Вследствие эффекта Доплера наблюдаемая частота

, Y\— (vie)* vfd

у =Z у — - — ι

1 — (ν/с) COS θ 1 — (vfc) COS ft "

Ей отвечает длина волны λ = c/v = d (c/v — cos θ¹). При ft = 45° и ν ^c длина волны λ «»0,6 мкм.

213. а) Пусть ν_χ—проекция вектора скорости излучающего атома на направление линии наблюдения. Число атомов с проекциями V_xt v_x + dv_x

^п (^vx) ^άυχ ~ ^exP {~^mvli^2kT)' ^άϋχ-

Частота света, излучаемого атомами, скорость которых V_xf есть ω = ω₀ (1+ t>_x/c). С помощью этого выражения найдем распределение атомов по частотам:

η (ω) άω = η (ν_χ) dv_x. И наконец, надо учесть, >Р что спектральная интенсивность излучения

Ι_ω ~ η (ω). б) Δω/ω₀ = 2 Y(2 In 2) kT/tnc².

213. и= ⁰Jⁿ_t^^v . Если V <C_t то 1 + V/сп ^

"4+^-4)-

213. ν = ¹Z₂Cbft = 30 км/с, 5.242. θ'= 8°.

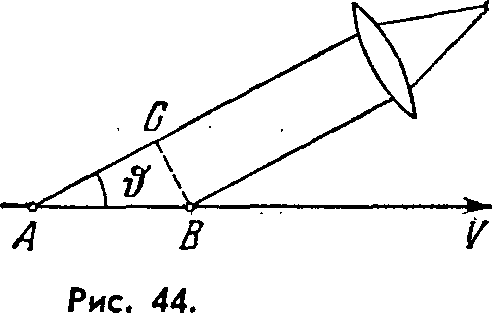
5.243. Движущаяся со скоростью V заряженная частица своим полем воз­буждает атомы среды, и они становятся источниками световых волн. Возьмем две произвольные точки А и В на пути движения частицы. Световые волны, испускаемые из этих точек при прохождении через них частицы, достигнут точки P (рис. 44) за одинаковое время и усилят друг друга, если время рас­пространения световой волны из точки А в точку С будет равно времени про­лета частицей пути AB. Отсюда получим cos θ = о/К, ^гД^е v = c/n—фазовая

скорость света. Видно, что излучение возможно лишь при V ;> ν, т. е. когда скорость частицы больше фазовой скорости света в среде.

244. T_wm = (п/Vn²- 1 — 1) тс²; соответственно 0,14 МэВ и 0,26 ГэВ. Для μ-мезонов.

245. T= ( - - Л тс² = 0,23 МэВ.

\ vn² cos² o-i )

247. T₂ = bT₁ftb + T₁AK)=\J5 кК.

248. λ^ = 3,4 мкм.

249. 5 . 10» кг/с, около IO¹¹ лет.

250. T = Y3cRpjoM = 2 - IO⁷ К, где R — универсальная газовая постоян­ная, М — молярная масса водорода.

251. t = (rp—l)cp d/\8oT% = 3 ч, где с—удельная теплоемкость меди, ρ—ее плотность.

252. T₂ = T₁Vdpl = QA кК.

253. a) C_v=(dU/dT)_v= \&jT*V/c=3 нДж/К, где U = AoTWIc; б) S = = 1баГзК/Зс=1,0 нДж/К.

254. a) G)_Bep = 2Γ/α = 5,24 · IO¹⁴ рад/с; б) К_вер = 2лса/5Т = 1,44 мкм,

255. a) u_tii = (кТ/п²с*) ω²; б) =

^ν3 16я²Шг⁵

247. M_v = U_k =

5.257. АР = 4д²с²ЛГ5ДЯ/Ь5(е^2л^—1) = 0,31 Вт/см², где постоянная в законе смещения Вина.

5.258., а) 1,1 мкм; б) 0,37; в) PzlPi = (T₂IT₁)* (l—y₂)ft\-_У1) = 4,9.

, 1 ω^ω 8πλ~Μλ

259. _η<ύάω=— _/i(d/kT__r ηχάλ = ^^—^.

260. a) <j) = PXI8n²cHr* = 6- ΙΟ*³ см^-с"*; б) r = V РХРЪп/2пс=9 м.

261. dpIdt = Ф_э/с.

262. (р ) = 4 (1 + р) Elnd²CX ^ 50 атм.

263. ρ = (Elc) 1 + р² + 2р cos 20=35 нН · с.

264. р = (//с) (1 + р) cos² 0 = 0,6 нН/см²,

265. /^? = я^²//с = Ь,18 мкН.

266. Р = />/2с(1+г]²).

267. a) Ap=^- _χ ; б) Δρ = Здесь $=Vlc. Видно,

что в системе отсчета, связанной с зеркалом, последнему передается меньший импульс.

259. sin (0/2) :¾ Elmc VW* 0=0,5°.

260. Δω/ωο=— (l — e~~^yM/Rc2) <0, т. е. частота фотона уменьшается,

261. U = 2пНс (1 — 1/η)/βΔλ = 16 кВ.

262. U = nftcled sina = 31 кВ.

263. %_mm = 2nH/rnc(y — 1) = 2,8 пм, где у =Ifyⁱ{ — (vfc)².

264. 332 нм, 6,6- 105 м/с.

265. ^=2π^^²~^λ2/^^}=1,9 эВ. A₂ (η-—ij

266. ф„акс = ⁴»⁴ В.

267. Г_маКс==Й(о)₀ + о>)-- Л_ВЬ1Х=0,38 эВ.

268. w = 2nc1iJ/eX = 0,020.

269. ^_m8Kc = 6,4· 105 м/с.

270. 0,5 В; ее полярность противоположна полярности внешнего напря* же.иия.

271. Ь/тс—комптоновская длина волны данной частицы.

272. Запишем законы сохранения энергии и импульса в системе отсчета, связанной с электроном —до соударения с фотоном: йо) + /я₀с² = /яс². Λω/ce

*=mv, где т = m_Q Y\ —(v/c)². Отсюда следует, что с;=0 или с. Оба резуль* тата физического смысла не имеют.

259. а) Рассеяние происходит иа свободных электронах; б) увеличи·» вается число электронов, которые становятся свободными (под свободными понимаются электроны, энергия связи которых значительно меньше энергии, передаваемой им фотонами); в) наличие несмещенной компоненты объясняется рассеянием на сильно связанных электронах и на ядрах.

260. [sin (^2/2)-η sin (<у2)]/(т]—1) = 1,2 пм.

261. Γ = ^ωη/( 1 +η) = 0,20 МэВ.

1 +ктс/2лН

2лxhj%

259. а) ш'=2яс/(Я+2яй/тс) = 2,2.10²« _рад/_с; б) Г = = 60кэВ.

260. to'= . , _{0 /<8} . _/<V/0 =0,144 МэВ.

1+2 (Иы/тс²) sin (#/2)

259. sin (ft/2) = Yтс (p — p^f)/2pp^f, отсюда ft= 120*.

260. fa)=[l +У\+2тс²!Т sin³ (ft/2)] 772 = 0,68 МэВ.

261. λ = (2nfi/mc) (Kl+2тс^а/Г_маКС—1) = 3,7 пм.

*oon irrn V^H/mcAX— 1 _m ⁵·²⁹⁰· ^tg^ 1 + fito/mc² ' ^³¹ ·

291. p = ²^⁽i^CM·

292. Δλ = (4ti/mc) sin² (ft/2) = 1,2 пм.

1. r = 3e²/2£ = 0,16 нм, λ = (2яс/е) }/mr» =^0,24 мкм.

2. 6 = 0,73 пм.

⁶·³· ^а) ^rMHH=⁰'^{59 б}) ^гмин-(2^²/Г)(1+т_а/т_и)=0,034 пм.

4. а) Рмин=(^²/Г) Ctg² (ft/2) = 0,23 пм; б) г_НЙН = [1+csc (ft/2)] Ze*fT = авр 0,56 пм.

5. р^ 2 Y2mTj[\ + (2bT/Ze²)²].

6. T_e = m_pe*/m_eb²T=4 эВ.

„„ . #n sin (ft/2)

4. 6= . ^{v 7} _гле п=1Л + С/а/Г.

Z1 + n²—2/гcos (ft/2) · ^{д v L}^^Uo/I

4. a) cos (ft/2) = b/(R + r); 6) ^iP=V₂ sin ft dft; в) Я=¹/*

5. 3,3. 10-δ.

6. d=*(4JT^zT²ZnIZ²*) sm* ($/2)=1,,5 мкм, где η — концентрация ядер.

7. Z_pt = Z_Agyr0_ptM_Ag = 78.

8. а) 1,6-106; б) N = Knd(Ze²ZT)² ctg² (fto/2) /₀τ = 2,0. IO⁷, где п — кон­центрация ядер.

9. P = Ktid (Zt?²/mu²)² = 0,006, где л—концентрация ядер.

10. AN/N= 1 —πηΖ4*/Τ* tg² (0/2) = 0,6,

11. = = где Z_i и

Z₂-порядковые номера меди и цинка, Afy и M₂ — их молярные массы, А^д —число Авогадро.

4. Δσ = π (Ze²/Т)² ctg² (О₀/2) = 0,73 кб.

5. а) 0,9 МэВ; б) do/dQ = Δσ/4π sin⁴ (0/2) = 0,64 кб/ср.

6. t=(Зтс*/2е²<й²) In η = 15 не.

7. t ъа гп*<*г*/4е* ** 13 пс.

21. r_n=Vnhjm<i)_t E_n = IiTm_t где я=1, 2, ..., <d = Vk/m*

•	Ги ПМ	Vt 10е м/с	Tt эВ	E , эВ ев*	Ф/, в	Φι, В	λ, HM
H He+	52,9 26,5	2,18 4,36	13,6 54^5	13,6 54,5	13,6 54,5	10,2 40,8	121,5 30,4

21. u> = m<*Z²/hM² = 2fi7 рад/с.

22. \i_n = neti/2mc, μJM_n = e/2mc_t μ_Α = μ_5#

23. £ = m²e⁷/^ = 125 кГс.

27. Серия Брэкета, λ₆^₄=2,63 мкм.

28. а) 657, 487 и 434 нм; б) λ/δλ=^ 1,5 -10».

29. При м>1 значение sin ОIt³KcJlR_i откуда 0^60%

30. He^.

31. AZ=¹M(^-I).

32. 97,3, 102,6 и 121,6 нм.

33. /1 = 5.

34. IO^rt

35. 2=V (176/15) nc/RAX = 3, Li⁺+.

36. λ=(2πτ/Δω) (Ζ Kfl/Δω— l)/(2Z /Λ/Δω— ί) = 0,47 мкм.

37. -Бсв=54,4 эВ (He⁺).

38. £ = £₀+4йД=79 эВ.

39. V 2 (to—4fiR)/m=2,3- IO⁶ м/с, где ш=2ясД.

40. Γ,,ηη = = 20,5 эВ.

41. у = 3tiR/4mc=3,25 м/с, где /я —масса атома.

42. (ε—ε⁷)/ε 3HR/Smc² = 0,55 · 10~^β %, где m —масса атома·

43. ν=2 VfiRjm=3,1 · 10^е м/с, где /и—масса электрона.

44. α=3£Δλ/8π cos 0=0,7* 10« м/с.

45. a) E_n=n²K²Ti²/2ml²\ б) E_n = n²ti²/2mr*; в) Е_я=лй]/аJinv г)

5= — та²/2И²п².

27. £"_св = где μ —приведенная масса системы. Без учета движения ядра эти величины для атома водорода больше на т/М<ы 8*0,055%,' где т и М—массы электрона и протона.

28. E_d-E_h = ZJ мэВ, X_h—λ₀ = 33 пм.

29. а) 0,285 пм, 2,53 кэВ, 0,65 нм; б) 106 пм, 6,8 эВ, 0,243 мкм.

30. 123, 2,86 и 0,186 пм.

31. 0,45 кэВ.

32. Для обеих частиц X = 2nfi (i m_nJm₍/}jV2m_nT = S_tQ пм.

33. 1 = 2 Х^УЦ + Ц.

34. X=2nbjY2mkT = 128 пм.

35. Найдем сначала функцию распределения молекул по дебройлевским длинам волн. Из соотношения / (у) dv = — φ (λ) dX_t где f (ν) — максвелловская функция распределения по скоростям, получим

φ (λ) = Αλ-*ζ~^α/λ\ a = 2n^?fi²jmkT.

Условие ίίφ/<ίλ = 0 дает λ_Βθρ = π П/У mkT = 0,09 нм.

27. λ = 2nhjV~2mT (1 -f Tj2mc²)_t T < 4/η<;²Δλ/λ = 20,4 кэВ (для электрона) и 37,5 МэВ (для протона).

28. T = (f2-i) mc² = 0,21 МэВ.

29. λ = Xjy^rI + mcXjnft = 3,3 пм.

30. v = 4nfilJmbAx = 2fi- IO⁶ м/с.

31. Δ* = 2ntiljd Ϋ2me U = 4,9 мкм.

32. UQ = Tfiti²(2me (ΐ^η — l)² d² sin² θ¹ = 0,15 кэВ.

33. d = KhklY2mT cos (ft/2) = 0,21 нм, где & = 4.

34. d = Tifiki\^r2mT sin ft = 0,23 ± 0,04 нм, где £ = 3 и угол ft опреде­ляется формулой tg2ft = D/2/.

35. a) n = VT+UJ/U= 1,05; б) UjU_i ^ 1/η (2+η) = 50.

36. E_n = n²n²fi²j2ml²_t где η= 1, 2, ...

66. 1 . IO⁴, 1 ■ 10 и 1 . 10-20 _см/с. .

67. Av^fiJml = 1 - IO⁶ м/с; ϋ_χ = 2,2·10⁶ м/с.

69. М^цтР/П^ 10 ¹⁶ с.

70. Г_мин^/*²/2т/²=1 эВ. Здесь взято ρ Ap и Ax = L

71. AvJv ~ TiJl y^r2mT = 1 ·

72. F ^ Ti²Jml^z.

73. Имея в виду, что ρ ~ Ap ~ fi/Ax ~ TiJx_t получим E = T+ LJ^

c^ti²j2mx²-\-kx²j2. Из условия dEjdx = 0 находим х₀ и затем E_jauh^ Ti YkJm = = Tm_t где ω —круговая частота осциллятора. Точный расчет дает /ζω/2.

69. Имея в виду, что p~Ap~TiJAr и Ar~r_t получим E = p²j2m~— — e²jr ^Ti²j2mr²—e²jr. Из условия dEjdr = 0 находим г_Эфф ^ Ii²Jme!¹ = 53 пм, ^мин Vie⁴JZft² = — 13,6 эВ.

70. Ширина изображения Δ % δ + Δ' ^ts δ + /ζ//ρδ, где Δ'—дополнитель­ное уширение, связанное с неопределенностью импульса Ap_y (при прохождении через щель), р — импульс падающих атомов водорода. Функция Δ (δ) имеет

минимум при δ ^Y Mjmv = Ofil мм.

69. Решение уравнения Шрёдингера ищем в виде Ψ=ψ (jc) · f (t). Под­становка этой функции в исходное уравнение и разделение переменных χ и t

привсдит к двум уравнениям. Их решения: ψ (л:) ~e^lkx_t где k = Y2mEjTi_t 336

Ε — энергия частицы, и ^ι<ύί, где (H = EjTu В результате ψ =Seeⁱ^^ettil_t

где α —некоторая постоянная.

6.77. Р=1/з + КЗ/2я = 0,б1.

A cos (nfixjl)y если η = U 3, 5, ...,

A Sm(Rnxjl)_i если п = 2, 4, 6, ...

Здесь Л = γι/Ι.

80. dNjdE = (IjnTi)Vtnj2E; при E=I эВ величина dNjdE =0,8· 101 уровней/эВ.

81. а) В этом случае уравнение Шрёдингера имеет вид

+ Л» = 2 «£/*■.

Возьмем начало координат в одном из углов ямы. На сторонах ямы функ­ция ψ (χу у) должна обращаться в нуль (по условию), поэтому внутри ямы ее удобно искать сразу в виде ψ (х_у у) = а Sink₁X * smk₂y_f так как на двух сто­ронах (дг=0 и у = 0) автоматически ψ = 0. Возможные значения ki и k₂ найдем нз условия обращения ψ в нуль на противоположных сторонах ямы:

= £ι = ± (η/ίί) tit* I₁ = I_f 2, 3, ..., ψ(*, I₂) = 0, k₂ = ±:(njl₂) n₂ = l, 2, 3, ...

Подстановка волновой функции в уравнение Шрёдингера приводит к соотт> шению + &! = £-, откуда

= («ι/^ϊ -ь

б) 9,87, 24,7, 39,5 и 49,4 единиц WjmP.

80. P = V₃-К5/4л;=19,5<%.

81. a) E = (n\+nl + nl)n4²j2ma?, где «₃ —целые числа, не рав­ные нулю; б) AE = n4i²jma-; в) для 6-го уровня n?-f nf +л| = 14 и E = = 7пШ*/та²; число состояний равно шести (оно равно числу перестановок тройки чисел 1, 2 и 3).

82. Проинтегрируем уравнение Шрёдингера по малому интервалу коорч динаты X_f внутри которого имеется скачок U (X)_j например в точке * = 0:

дх

-д

Ввиду конечности скачка U при δ 0 интеграл тоже стремится к нулю· Дальнейшее очевидно.

6.85. а) Запишем уравнение Шрёдингера для двух областей:

OcxcU ΨΓ + *'²Ψι = & = 2m£/fi²,

x>U ψ;—X²Xp₂ = O_f к² = 2т (U₀-E)IhK

Их общие решения

ί.78. φ ==|

* о

(+£)-|·-(-δ)= ) ~ (E-U)^dX.

(л;) = α sin (&*+α), ψ₂ (*) = ^-**+^*.

337

голжны удовлетворять стандартным и граничным условиям. Из условия If₁(O) = O н требованяя конечности волновой функции следует, что α = 0 и C=O. И наконец, из непрерывности ψ (*) н ее производной в точке х=1

■J2 И. Е. Иродов

получим tg&I=—β/κ, откуда

sin kl=±kl Vti²/2ml²U₀-

Изобразив графически левую и правую части последнего уравнения (рис* 45), найдем точки пересечения прямой с синусоидой. При этом корни данного уравнения, отвечающие собственным значениям энергии £, будут соответствовать тем точкам пересечения (£/)/, для которых tg (kl)i < 0, т. е.

участки оси абсцисс выделены на рисунке жирными отрезками). Из графика видно, что корни уравнения, т. е. связанные состояния частицы, существуют не всегда. Пунктиром показано предельное положение прямой, ¢) (ГОо^мин =³ «= Jt²fi²/8m, (I²U₀)_{n мин} = (2п — 1) π²Η²βт.

86. Пусть P_a и Pi—вероятности нахождения частицы вне и внутри ямы. Тогда

OO

С ^^2kx dx

Pg ₌ i 2

P_i i 2+Зя »

\ a² sin² kx dx

где отношение bja можно определить из условия ψι (Z)=^fe (0· Остается учесть, что P_a^P_i= 1; тогда P_tt=2/(4+ Ззх) = 14,9%.

Возможность нахождения частицы в области, где ее энергия EcU_f пред­ставляет собой чисто квантовый эффект. Он является следствием волновых свойств частицы, исключающих одновременно точные значения координаты и импульса, а следовательно, и точное разделение полной энергии частицы на потенциальную и кинетическую. Последнее можно сделать только в пределах точности, даваемой соотношением неопределенностей.

86. В результате указанной подстановки получим

χ" + />2_χ==ο, где k²=2тЕ/П².

Решение этого уравнения ищем в виде χ = α sin (&r + a). Из требования конеч­ности волновой функции ψ в точке г = O следует, что а = 0. Таким образом, yp=(a/r) sin kr. Из граничного условия -ψ (r₀) = О получим кг₀ = пя, где η =а «= 1, 2, ... Отсюда E_n=n²n²n²j2mf%,

86. а) φ (г)= ^ⁿ (^nnrZr₉) 2, б) ^_ep = O/2: 50%.

у 2π/·₀ г

86. а) Решения уравнения Шрёдингера для функции χ (г):

'Со, χι = Л sin (ft/·+а), где k =V^cIftiEjbr г>г₉, = +Cq-w, где χ^Y2т (U₉-E)Jfl.

Из требования ограниченности функции ψ (г) во всем пространстве следует, что CC = O и B = 0, Таким образом:

Из условия непрерывности ψ и ее производной в точке /· = /> получим tgkr₀= — &/κ, или

sin fcr₀ = ± VtPI2mrlU₀ kr_Q.

Это уравнение, как показано в решении задачи 6.85, определяет дискретный спектр собственных значений энергии, б) ^U₀=Ji²H²JSm.

86. a = m<o/2fi, E = Λω/2, где о»=J^iTm.

87. £ ——metJSb², т. е. уровень с главным квантовым числом я=2.

88. а) [Вероятность нахождения электрона на расстоянии г, r + dr от ¹ ядра ίίΡ=ψ²(/·) 4π/*² dr. Из условия максимума функции dP/dr получим

Гвер^п; б) (F)=2e²/r²; в) {U)=-e²Jr_u

86. ψο —^ (р/г) 4яг² dr=e/ri, где ρ =^—объемная плотность заряда,

ψ—нормированная волновая функция.

86. а) Запишем решения уравнения Шрёдингера слева а справа от гра* ницы барьера в следующем виде:

χ < о, ψι (*) = O₁Q^ikl* + he~ ^ikt*> где k± = УЪтЕ/Ъ,

χ > 0, ψ₂ (*) = Oze^ikt* + Ь&Ггде k_z=V2m (E-U₉)Jb.

Будем считать, что падающая волна характеризуется амплитудой Ci₁, а отра* женная — амплитудой 6_а. Так как в области Jt >0 имеется только проходя­щая волна, то ^₂ = 0. Коэффициент отражения R представляет собой отноше^ ние отраженного потока частиц к падающему потоку, или, другими словами, отношение квадратов амплитуд соответствующих волн. Из условия непрерыв­ности ψ и ее производной в точке * = 0 имеем As₁-^b₁ = O_s и а± — bi =s (k₂/ki) α₂, откуда

R=CW³ - {ki-k&Kkt +k₂)K

б) В случае E <1 U₉ решение уравнения Шрёдингера справа от барьера имеет вид

ψ₂ (х) = а₂е^х*+где κ=Y2m (U₉-E)Jb.

Из требования конечности ψ (я) следует, чт& Ct₂=0. Плотность вероятности нахождения частицы под барьером P₂ (л:)=(х) ~ е~^зкл\ Отсюда χ₉φφ = 1/2κ.

95. a) D exp J- Ц- Y2m (U₉—Е) j;

96. D exp [- j/"^- (t/_e-£)l.

97. —0,41 для S-терма и —0,04 для P-терма,

12* 339

96. a = VfiRKEo—eq>i) — 3=—0,88.

97. £_св = tiR/if RX₁X₂PjicAI — 1 )² = 5,3 эВ.

98. 0,82 мкм (3S->2P) и 0,68 мкм (2P-*2S).

99. Δ£ = 2π&:Δλ/λ² = 2,0 мэВ.

100. Δω= 1,05 - IO¹* рад/с.

101. 3S_w 3P_w 3P_w 3D_W 3D_bu.

102. а) 1, 2, 3, 4, 5; б) 0, ί, 2, 3, 4, 5, 6; в) % ⁸Z₂. ⁷/а> ^eZa-

103. Для состояния ⁴P: й j/"3/2, ft ^15/2 и Ii V35/2; для состояния §D:

0, й й/6, ЛуЧЗ, й У"20.

96. a) ²P₇,, M „ =й|/"63/2; б) зр M = 2¾/^

⁷ V* макс ' J > / 4' макс ^г

96. В Р-состоянии M_s = fi Vfy для D-состояния можно лишь устано­вить, что M_s ^ Ti V^f

97. 3, 4, 5.

98. а) 1, 3, 5, 7, 9; б) 2, 4, 6; в) 5, 7, 9. ,

99. 31^е. С

100. ³D₂.

101. IP₁, ^D₂, *Рз, V_0if,* ³D_1j2j3, ^_3j4.

102. Те же, что в предыдущей задаче,

103. Второй и третий.

104. g = 4+6= 10,

105. 4, 7 и 10,

"2 ^ft^

Рис. 46.

перпендикулярных плоскостях. Всего, таким образом, четыре разных колеба­ния. б) См. рис. 46,6; всего разных колебаний семь: три продольных ω₂, <оз) и четыре поперечных (ω₄> <оь) — по два на каждую частоту. 6.182. άΝ_ω =.(l/nv)dto.

183. άΝ_ω = (8/2πν²) ω άω*

184. <*ΑΤ_ω = (Κ/π²ϋ³)ω²<ίω.

185. a) Q = (Hfk)Kvn₀; 6) B=(Hfk) ν V4τΰζ; в) &=(fi/k) ν ^^r6π^₀".

186. θ = (HIk) У 18+2νJ³) == 470 К, где концентрация атомов.

187. ν kB/П I⁷ 6л²л₀ = 3,4 км/с, где л₀ —концентрация атомов. Таблич* ные значения: ^ = 6,3 км/с, t>j_=3,l км/с.

188. Колебательная энергия моля «кристаллая

U = RB

Θ/Τ

/JT\2 С XdX

4 ⁺\ θ ) ) е*—1 о

где χ—Ηω/kT* Отсюда молярная теплоемкость

2Т В

е/г

C = R

в/T

i ^xdx J е*— I

При T ^ θ теплоемкость C^R.

183. a) dN/d<o=2l/nctV^6ytiaKc~~^<i^; б) /V = //а, т. е. равно числу атомов в цепочке.

184. ί/₀ = 9£θ/8μ=4&,6 Дж/г, где μ—молярная масса меди.

185. а) θ «»220 К; б) C^lO Дж/(моль · К); в) о_макс = 4,1. IOi? _рад/_Св

193. Да, так как при этих температурах ^ теплоемкость пропорциональна TK

194. (E)

195. См. рис. 47.

196. Йо^_макс=2в шВ> Й^кс^Ю"^ г · см/с·

197. а) Г_макс =^ (Ззте%)^2>/3 б) (T) = V₆^aKc-

198. η= 1 — 2~^3/3 ^65%.

199. 0,93.

200. ^3 - IO⁴K.

201. (3π%)^1/3=2· 1(>~^эВ«

202. a) dn_v = (m3fn4i*} v*dv; б) (o}/t>_MaKc=

203. άηχ = 8πλ~⁴ ίίλ.

204. р=²/зД (7¹) = (л у^9л;/?²/5т) л^5/3^ 5 . IO⁴ атм.;

205. Л = &Г(л7УДГ—2)=4,5 эВ.

206. rt = Kl + U₀JT = 1,02, где £/₀=Г_макс+Л, Г_макс = {3^«)²%²/2т, Л—работа выхода·

6.207. P мин —

1 до 6.208. a=—-

ρ дТ

26 Γι T₂

-Inii=O,33 эВ.

Ticfl

= —0,05 К'¹,

£Γ²λ_κ

рииа запрещенной зоны.

6.209. AE= —2k =1,2 и 0,06 эВ.

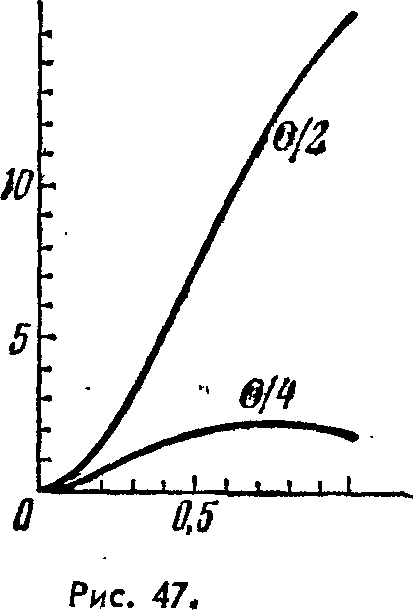
маке

Δ (Г η

210. τ-//In -f Pi) Рг _q ο 1 с.

(P-P₂)Pi

210. n=hBU JelpV _Н = Ь- 10^ _См~з, U₀^lV_nJhBV = 0,05 м²/(В-с).

211. I IQ-U+ | = 1/ηβ = 0,20 м2/(В · с).

212. η⁺/η~ = η² = 4,0.

213. a) P = 1 —ехр (— λ/); б) τ = 1/λ.

214. Около ι/*·

215. 1,2-1015.

216. τ ^ 16 с.

217. T=5,3 сут.

218. 4,6- IO² част./мнн.

219. λ=—(1/0 In (1—η) ^ η//*= 1,1 .10-5 <г\ т = 1/λ= 1,0 года,

220. T = 4,5-10» лет, A=I,2· IO⁴ расп./с.

221. 4,1 ■ Юз _лет.

222. Около 2,0 -10» лет.

223. Соответственно 3,2 · IO¹⁷ н 0,8 ■ IO⁵. расп.Дс · г).

224. V = (AjA^f) ехр (— t Iri 2/Г) = 6 л. , 6.226. 0,19%.

227. F₁ = I,6 ч, T₂ = 9,8 ч; N₂JN₁ = (T₂IT₁) ехр (In A₂-In A₁) = 10.

228. (T/ln 2) In (1 — А/?) = 9,5 сут.

229. a) yvnO-^o^Vie'^-e-^); б) ^IMW .

A₂ — Λί Αχ — A₂

227. a) N₂ (t) = ^Niot ехр (—λί)\ б) Z_m= 1/λ.

228. N₃ (t) = N₁₀ (l + ).

229. = iV^iехр (—λιΟ = 0,72. Юн част./с, N_a=N₀ —е"^II*') X X λιλ₂/(λ₂—λί)= 1,46. IO^III част./с. Здесь N₉ — первоначальное число ядер Bi²¹⁰.

230. а) Pb²⁰⁶; б) восемь α-распадов и шесть β-распадов.

231. ν = VImvTjtn = 3,4-10⁵, м/с; 0,020.

232. 1,6 МДж.

233. 0,82 МэВ.

234. а) 6,1 см; б) соответственно 2,1. 10^ н 0,77 - 105.

250. а) η = 4™ΑΓ/(/η + Α4)²=0,89; б) <r)=2mj(m + М) = ²/_э. Здесь т и Al — массы нейтрона и дейтона.

251. $_MaKc = arcsin (Zn₁Zm₂) = 30°, где т_х и W₂-массы протона и дейтона,

252. 2 . IO¹¹ кг/см³, 1 · IO³⁸ нуклон/см³,

253. a) d; б) Fi⁷; _в) а; г) Cl³⁷.

255. Be», £_св = 56,5 МэВ.

256. а) 8,0 МэВ; б) 11,5 и 8,7 МэВ; в) 14,5 МэВ.

257. E_n-E_p = 0,22 МэВ.

258. Ε = 20ε_Νβ — 2 ·4ε_α— 12е_с=11,9 МэВ, где ε—энергия связи на один

нуклон в соответствующем ядре.

255. а) 8,0225 а. е. м.; б) 10,0135 а. е. м.

256. Q = (E₃ + £4)-(£I + £₂)·

257. а) 8,2- IO¹⁰ кДж, 2,7 . IO⁶ кг; б) 1,5 кг.

258. 5,74- IO⁷ кДж; 2 . IO⁴ кг.

259. 2,79 МэВ; 0,85 МэВ.

260. ρ = 8ε_α—7e_Li = 17,3 МэВ.

261. Q = (1 +rjp) Т_р-(1 —η_α) Τ_α-2 /η_ρη_αΓ_ρΤ_α cos θ= -1,2 МэВ, где

%^^т_Р'^тО> V^^mJ^mO-

255. а) —1,65 МэВ; б) 6,82 МэВ; в) —2,79 МэВ; г) 3,11 МэВ.

256. ι>_α = 0,92. 10? м/с, t> _u = 0,53- IO⁷ м/с.

257. 1,9 МэВ.

258. T_n= β+j¹ "^m^^mC) ^r^_8lS МэВ.

1 + т_п/т_с

6.270 . 9,1 МэВ, 170,5°.

272. T^E^(m_p + m_d)jm_d=3,3 МэВ.

273. В пределах от 1,89 до 2,06 МэВ.

274. Q = — ΐ'/₁₂Γ_ΙΙ0ρ = —3,7 МэВ.

275. Соответственно 1,88 и 5,75 МэВ»

276. 4,4 МэВ; 5,3- IO⁶ м/с.

¹ * (m₄ — /H₁) T ^tH^A- Г_ПОр] = 2,2 МэВ, где т_ъ т_г>

Irt₁-^sTm₂ J

m₃ + m₄

т₄ —массы нейтрона, ядра С¹², α-частицы и ядра Be⁸.

278. На E_CB/2mc² = 0,06%, где т — масса дейтона.

279. E = Q+²/_zT = Q,5 МэВ.

т_с

278. E_i = Eco + T^hi—7^ = 16,7, 16,9, 17,5 и 17,7 МэВ, гдеЕ_св —

^mCi^^mC

виергия связи дейтона в промежуточном ядре.

278. σ = (Λί/Λ^Γρ d) In η=2,5 кб, где Al— молярная масса кадмия до _ число Авогадро, р —плотность кадмня.

279. /₀// = ехр [(2σ!+σ₂) nd]=20, где л —концентрация молекул тяжелой воды.

280. w={\ — ехр[— (σ₅+σ_α) nd]} σ₅/(σ₅+σ_α) = 0,3δ, где η —концентра­ция ядер железа.

281. a) T=(w/k) In 2; б) W = ATejit In 2 = 2 . 10~³.

282. 6.277. T_a =

     a) t= η/σ7 = 3· IO⁶ лет;- б) ' JV_aialtc V_eTyln 2= 1,0 . IO¹³, где N₆—число ядер Au¹⁹? в фольге.

283. Ν = (\—ν~^λ*) JnafX.

284. J=*Aefafetf₀(1 —е^) = 6· IO⁹ част,/(см²*с), где λ —постоянная рас·» пада, N₀-число ядер Au в фольге.

285. W = N₀fe'-*=1,3* IO⁶, где i — число поколений*

286. N=VPfE = 0,8-10¹⁹

287. а) ЛГ/ЛГ₀=4. IO²; б) Г = т/(4 —1)-=10 с.

288. Соответственно 0,05, 0,4 и 9 ГэВ.

289. </} — гг₀ Ι^η (η + 2) = 15 м,

290. T₀ = Imcfy^rT {Τ+2mc²) — 26 не, где m —масса покоя π-мезона.

291. JfJ₀-ехр [— Imclτ₀ V T (7^2//^ = 0,22, где т —масса покоя лг-мезона.

6.295*). Γ_μ = (™_Λ —^)2/2/% = 4Д МэВ, E_v^29,8 МэВ, 6.296*. Τ = [(τη_Σ — т_пу — mj]/2m_s ==19,5 МэВ.

6.297*. F_llaicc == (/π_μ—т_е)²/2т_д = 52,5 МэВ.

6.298*. m = Г + )//n®J + 7* (Г+2яг_р) = IllS МэВ, Λ —частица. 6,299*. = + ^{22 МэВ}'

6.300*. m==)/m|i + /n»~2(m₂ (m_rt + 7*_rt) =0,94 ГэВ, нейтрон.

6.301 *. Т_л = т_л [csc (9/2)-1], Ey = m^f2 sin (β/2). При 0 = 60* энергия

T⁵Ji = Ey =

6.303*. cos (0/2)^l/Kl+2m/7\ отсюда θ = 99<\

6.304*. а) C_nop = 4/¾ = 2,04 МэВ; б) е_пор = 2т_л (1+т_л/т_р) = 320 МэВ. 6.305*. a) T_nop = 6/л_р = 5,6 ГэВ; б) T_nop-т_л (4т_р+т_к)/2т_р=0,28 ГэВ.

306. а) 0,90 ГэВ; б) 0,77 ГэВ.

307. S= — 2, Y^r=-I, Ξ «-частица.

308. Запрещены 1, 2 и 3.

309. Запрещены 2, 4 и 5.

310. Энергетически (1); в остальных процессах не сохраняются: барион* ный заряд (2), электрический заряд (3), странность (4), лептонный заряд (5) и (6) — электронный и мюониый.

*) В ответах задач 6.295—6.305, отмеченных звездочкой, использовано со­кращенное обозначение: т вместо тс^г*

ПРИЛОЖЕНИЯ

1. Основные тригонометрические формулы

sin2 α+cos2 α = 1 sec2 а — tg2a = 1 CSC2 а — ctg2 а = 1 sin а · csc а = 1 cos а · sec а = 1 tg а · ctg а = 1	sin (а ± β) = sin α cos β ± cos α sin β cos (α dt β) = cos α cos β =T sin α sin β tg (α ±β)_ tf . & v 1 -Η tg α ■ tg β Vl ctg β Hr Ctga
1 sina= ■= Y\ +ctg2 а 1 cos а =-.. V 1 + tg2 а sin 2а = 2 sin a cos а cos 2а =cos2 а — sin2 а	. Λ ~ , α + β α —β sin a + sin β = 2 sin —cos — . 0 0 α + β„ί β sin α — sin β = 2 cos —sin —^jl ο ο α + β α —β cos a +cos β = 2 cos—^ cos — o . α + β . α —β cos a —cos β= — 2 sin —~ sin — . , n sin (a ± β) tga ± tgB= 4 & K cos a cos β , 0 sin (a ± β) ctg a±ctg β = ± ; —~ s ь r sm a sin β
. а ЛГ1 — cos а ЯП 2 = у 2 α Ί А1 + cos а cosT^y * 2—	2 sin a sin β = cos (α—β) —cos (α+β) 2 cosa cos β = cos (α—β)+cos (a + β) 2 sin a cos β = sin (a — β) + sin (a + β)
еа — е~а sh а = 2— е« + е~« cha== 2—	e« — e~« tha= ea + e a ,, ea + e~a ctha — ea — e~a

2. Таблица синусов

φ·

О*

40'

О'

20'

Ф^а

40'

20'

0,0000 0,0175 0,0349 0,0523 0,0698

0,0872 0,1045 0,1219 0,1392 0,1564

0,1736 0,1908 0,2079 0,2250 0,2419

0,2588 0,2756 0,2924 0,3090 0,3256

0,3420 0,3584 0,3746 0,3907 0,4067

0,4226 0,4384 0,4540 0,4695 0,4848

0,5000 0,5150 0,5299 0,5446 0,5592

0,5736 0,5878 0,6018 0,6157 0,6293

0,6428 0,6561 0,6691 0,6820 0,6947

2. 2 3

■ 4

8. 9

10 11 12

20. 21 22

0,0058 0,0233 0,0407 0,0581 0,0756

0,0929 0,1103 0,1276 0,1449 0,1622

0,1794 0,1965 0,2136 0,2306 0,2476

0,2644 0,2812 0,2979 0,3145 0,3311

0,3475 0,3638 0,3800 0,3961 0,4120

0,4279 0,4436 0,4592 0,4746 0,4899

0,5050 0,5200 0,5348 0,5495 0,5640

0,5783 0,5925 0,6065 0,6202 0,6338

0,6472 0,6604 0,6734 0,6862 0,6988

0,0116 0,0291 0,0465 0,0640 0,0814

0,0987 0,1161 0,1334 0,1507 0,1679

0,1851 0,2022 0,2196 0,2363 0,2532

0,2700 0,2868 0,3035 0,3201 0,3365

0,3529 0,3692 0,3854 0,4014 0,4173

0,4331 0,4488 0,4643 0,4797 0,4950

0,5100 0,5250 0,5398 0,5544 0,5688

0,5831 0,5972 0,6111 0,6248 0,6383

0,6517 0,6648 0,6777 0,6905 0,7030

0,7071 0,7193 0,7314 0,7431 0,7547

0,7660 0,7771 0,7880 0,7986 0,8090

0,8192 0,8290 0,8387 0,8480 0,8572

0,8660 0,8746 0,8829 0,8910 0,8988

0,9063 0,9135 0,9205 0,9272 0,9336

0,9397 0,9455 0,9511 0,9563 0,9613

0,9659 0,9703 0,9744 0,9781 0,9816

0,9848 0,9877 0,9903 0,9925 0,9945

0,9962 0,9976 0,9986 0,9994 0,9998

60. 61 62

    80. 81 82

        88. 89

0,7153 0,7274 0,7393 0,7504 0,7622

0,7735 0,7844 0,7951 0,8056 0,8158

0,8258 0,8355 0,8450 0,8542 0,8631

0,8718 0,8802 0,8884 0,8962 0,9038

0,9112 0,9182 0,9250 0,9315 0,9377

0,9436 0,9492 0,9546 0,9596 0,9644

0,9689 0,9730 0,9769 0,9805 0,9838

0,9868 0,9894 0,9918 0,9939 6,9957

0,9971 0,9983 0,9992 0,9997 1,0000

0,7112 0,7234 0,7353 0,7470 0,7585

0,7698 0,7808 0,7916 0,8021 0,8124

0,8225 0,8323 0,8418 0,8511 0,8601

0,8689 0,8774 0,8857 0,8936 0,9013

0,9088 0,9159 0,9228 0,9293 0,9356

0,9417 0,9474 0,9528 0,9580 0,9628

0,9674 0,9717 0,9757 0,9793 0,9827

0,9858 0,9886 0,9911 0,9932 0,9951

0,9967 0,9980 0,9989 0,9996 0,9999

3. Таблица тангенсов

20'

О'

φ¹

40'

φ¹

О'

20'

1,0000 1,036 1,072 1,111 1,150

1,192 1,235 1,280 1,327 1,376

1,428 1,483 1,540 1,600 1,664

1,732 1,804 1,881 1,963 2,050

2,145 2,246 2,356 2,475 2,605

2,747 2,904 3,078 3,271 3,487

3,732 4,011 4,331 4,705 5,145

5,671 6,314 7,115 8,144 9,514

1,012

1,048 1,085 1,124 1,164

1,206 1,250 1,295 1,343

1,446 1,501

560. 1,621 1,686

1,756 1,829 1,907 1,991 2,081

2,177 2,282

394. 2,517 2,651

2,798 2,960 3,140 3,340 3,566

3,821 4,113 4,449 4,843 5,309

5,871

561. 7,429 8,556

10,08

12,25 15,60 21,47 34,37 85,94

60. 61 62

    80. 81 82

        88. 89

0,0058 0,0233 0,0407 0,0582 0,0758

0,0934 0,1110 0,1287 0,1465 0,1644

0,1823 0,2004 0,2186 0,2370 0,2555

0,2742 0,2931 0,3121 0,3314 0,3508

0,3706 0,3906 0,4108 0,4314 0,4522

0,4734 0,4950 0,5169 0,5392 0,5619

0,5851 0,6088 0,6330 0,6577 0,6830

0,7089 0,7355 0,7627 0,7907 0,8195

0,8491 0,8796 0,9110 0,9435 0,9770

0,0116 0,0291 0,0466 0,0641 0,0816

0,0992 0,1169 0,1346 0,1524 0,1703

0,1883 0,2065 0,2247 0,2432 0,2617

0,2805 0,2994 0,3185 0,3378 0,3574

0,3772 0,3973 0,4176 0,4383 0,4592

0,4806 0,5022 0,5243 0,5467 0,5696

0,5930 0,6168 0,6412 0,6661 0,6916

0,7177 0,7445 0,7720 0,8002 0,8292

0,8591 0,8899 0,9217 0,9545 0,9884

0,0000 0,0175 0,0349 0,0524 0,0699

0,0875 0,1051 0,1228 0,1405 0,1584

0,1763 0,1944 0,2126 0,2309 0,2493

0,2679 0,2867 0,3057 0,3249 0,3443

0,3640 0,3839 0,4040 0,4245 0,4452

0,4663 0,4877 0,5095 0,5317 0,5543

0,5774 0,6009 0,6249 0,6494 0,6745

0,7002 0,7265 0,7536 0,7813 0,8098

0,8391 0,8693 0,9004 0,9325 0,9657

2

8. 9

10 11 12

20. 21 22

11,43 14,30 19,08 28,64 57,29

4. Таблица десятичных логарифмов

N	0	I	2	3	4	5	6	7	8	9
10	0000	0043	0086	0128	0170	0212	0253	0294	0334	0374
11	0414	0453	0492	0531	0569	0607	0645	0682	0719	0755
12	0792	0828	0864	0899	0934	0969	1004	1038	1072	1106
13	1139	1173	1206	1239	1271	1303	1335	1367	1399	1430
. 14	1461	1492	1523	1553 ,	1584	1614	1644	1673	1703	1732
15	1761	1790	1818	1847	1875	1903	1931	1959	1987	2014
16	2041	2068	2095	2122	2148	2175	2201	2227	2253	2279
17	2304	2330	2355	2380	2405	2430	2455	2488	2504	2529
13	2553	2577	2601	2625	2648	2672	2695	2718	2742	2765
19	2788	2810	2833	2856	2878	2900	2923	2945	2967	2989
20	ЗОЮ	3032	3054	3075	3096	3118	3139	3160	3181	3201
21	3222	3243	3263	3284	3304	3324	3345	3365	3385	3404
22	3424	3444	3464	3483	3502	3522	3541	3560	3579	3598
23	3617	3636	3655	3674	3692	3711	3729	3747	3766	3784
24	3802	3820	3838	3856	3874	3892	3909	3927	3945	3962
25	3979	3997	4014	4031	4048	4065	4082	4099	4116	4133
26	4150	4166	4183	4200	4216	4232	4249	4265	4281	4298
27	4314	4330	4346	4362	4378	4393	4409	4425	4440	4456
23	4472	4487	4502	4518	4533	4548	4564	4579	4594	4609
29	4624	4639	4654	4669	4683	4698	4713	4728	4742	4757
30	4771	4786	4800	4814	4829	4843	4857	4871	4886	4900
31	4914	4928	4942	4955	4969	4983	4997	5011	5024	5038.
32	5051	5065	5079	5092	5105	5119	5132	5145	5159	5172
33	5185	5198	5211	5224	5237	5250	5263	5276	5289	5302
34	5315	5328	5340	5353 -	5366	5378	5301	5403	5416	5428
35	5441	5453	5465	5478	5490	5502	5514	5527	5539	5551
36	5563	5575	5587	5599	5611	5623	5635	5647	5658	5670
37	5682	5694	5705	5717	5729	5740	5752	5763	5775	5786
38	5798	5809	5821	5832	5843	5855	5866	5877	5888	5899
39	5911	5922	5933	5944	5955	5966	5977	5988	5999	6010
40	6021	6031	6042	6053	6064	6075	6085	6096	6107	6117
- 41	6128	6138	6149	6160	6170	6180	6191	6201	6212	6222
. 42	6232	6243	6253 '	6263	6274	6284	6204	6304	6314	6325
43	6335	6345	6355	6365	6375	6385	6395	6405	6415	6425
44	6435	6444	6454	6464	6474	6484	6493	6503	6513	6522
45	6532	6542	6551	6561	6571	6580	6590	6599	6609	6618
46	6628	6637	6646	6656	6665	6675	6684	6693	6702	6712
47	6721	6730	6739	6749	6758	6767	6776	6785	6794	6803
48	6812	6821	6830	6839	6848	6857	6866	6875	6884	6893
49	6902	6911	6920	6928	6937	6946	6955	6964	6972	6981
50	6990	6998	7007	7016	7024	7033	7042 '	7050	7059	7067
51	7076	7084	7093	7101	7110	7118	7126	7135	7143	7152
52	7160	7168	7177	7185	7193	7202	7210	7218	7226	7235
53	7243	7251	7259	7267	7275	7284	7292	7300	7308	7316
54	7324	7332	7340	7348	7356	7364	7372	7380	7388	7396

Продолжение табл. 4

N	0	I	2	3	4	5	6	7	8	9
55	7404	7412	7419	7427	7435	7443	7451	7459	7466	7475
56	7482	7490	7497	7505	7513	7520	7528	7536	7543	7551
57	7559	7566	7574	7582	7589	7597	7604	7612	7619	7627
58	7634	7642	7649	7657	7664	7672	7679	7686	7694	7701
59	7709	7716	7723	7731	7738	7745	7752	7760	7767	7774
60	7782	7789	7796	7803	7810	7818	7825	7832	7839	7846
61	7853	7860	7868	7875	7882	7889	7896	7903	7910	7917
62	7924	7931	7938	7945	7952	7959	7966	7973	7980	7987
63	7993	8000	8007	8014	8021	8028	8035	8041	8048	8055
64	8062	8069	8075	8082	8089	8096	8102	8109	8116	8122
65	8129	8136	8142	8149	8156	8162	8169	8176	8182	8189
66	8195	8202	8209	8215	8222	8228	8235	8241	8248	8254
67	8261	8267	8274	8280	8287	8293	8299	8306	8312	8319
68	8325	8331	8338	8344	8351	8357	8363	8370	8376	8382
69	8388	8395	8401	8407	8414	8420	8426	8432	8439	8445
70	8451	8457	8463	8470	8476	8482	8488	8494	8500	8506
71	8513	8519	8525	8531	8537	8543	8549	8555	8561	8567
72	8573	8579	8585	8591	8597	8603	8609	8615	8621	8627
73	8633	8639	8645	8651	8657	8663	8669	8675	8681	8686
74	8692	8698	8704	8710	8716	8722	8727	8733	8739	8745
75	8751	8756	8762	8768	8774	8779	8785	8791	8797	8802
76	8808	8814	8820	8825	8831	8837	8842	8848	8854	8859
77	8865	8871	8876	8882	8887	8893	8899	8904	8910	8915
78	8921	8927	8632	8938	8943	8949	8954	8960	8965	8971
79	8976	8982	8987	8993	8998	9004	9009	9015	9020	9025
80	9031	9036	9042	9047	9053	9058	9063	9069	9074	9079
81	9085	9090	9096	9101	9106	9112	9117	9122	9128	9133
82	9138	9143	9149	9154	9159	9165	9170	9175	9180	9186
83	9191	9196	9201	9206	9212	9217	9222	9227	9232	9238
84	9243	9248	9253	9258	9263	9269	9274	9279	9284	9289
85	9294	9299	9304	9309	9315	9320	9325	9330	9335	9340
86	9345	9350	9355	9360	9365	9370	9375	9380	9385	9390
87	9395	9400	9405	9410	9415	9420	9425	9430	9435	9440
88	9445	9450	9455	9460	9465	9469	9474	9479	9484	9489
89	9494	9499	9504	9509	9513	9518	9523	9528	9533	9538
90	9542	9547	9552	9557	9562	9566	9571	9576	9581	9586
91	9590	9595	9600	9605	9609	9614	9619	9624	9628	9633
92	9638	9643	9647	9652	9657	9661	9666	9671	9675	9680
93	9685	9689	9694	9699	9703	9708	9713	9717	9722	9727
94	9731	9736	9741	9745	9750	9754	9759	9763	9768	9773
95	9777	9782	9786	9791	9795	9800	9805	9809	9814	9818
96	9823	9827	9832	9836	9841	9845	9850	9854	9859	9863
97	9868	9872	9877	9881	9886	9890	9894	9899	9903	9908
98	9912	9917	9921	9926	9930	9934	9939	9943	9948	9952
99	9956	9961	9965	9969	9974	9978	9983	9987	9991	9996

5. Показательные функции

JC	е*		X	е*	е-*
0,00	1,0000	1,0000	2,00	7,3891	0,1353
0,05	1,0513	0,9512	2,05	7,7679	0,1287
0,10	1,1052	0,9048	2,10	8,1662	0,1225
0,15	1,1618	0.8607	2,15	8,5849	0,1165
0,20	1,2214	0,8187	2,20	9,0250	0,1108
0,25	1,2840	0,7788	2,25	9,4877	0,1054
0,30	1,3499	0,7408	2,30	9,9742	0,1003
0,35	1,4191	0,7047	2,35	10,486	0,09537
0,40	1,4918	0,6703	2,40	11,023	0,09072
0,45	1,5683	0,6376	2,45	11,588	0,08629
0,50	1,6487	0,6065	2,50	12,182	0,08208
0,55	1,7333	0,5770	2,55	12,807	0,07808
0,60	1,8221	0,5488	" 2,60	13,464	0,07427
0,65	1,9155	0,5221	2,65	14,154	0,07065
0,70	2,0138	0,4966	2,70	14,880	0,06721
0,75	2,1170	0,4724	2,75	15,643	0,06393
0,80	2,2255	0,4493	2,80	16,445	0,06081
0,85	2,3396	0,4274	2,85	17,288	0,05784
0,90	2,4596	0,4066	2,90	18,174	0,05502
0,95	2,5857	0,3867	2,95	19,106	0,05234
1,00	2.7183	0,3679	3,00	20,086	0,04979
1,05	2,8577	0,3499	3,05	21,115	0,04736
1,10	3,0042	0,3329	3,10	22,198	0,04505
1,15	3,1582	0,3166	3,15	23,336	0,04285
1,20	3,3201	0,3012	3,20	24,533	0,04076
1,25	3,4903	0,2865	3,25	25,790	0,03877
1,30	3,6693	0,2725	3,30	27,113	0,03688
1,35	3,8574	0,2592	3,35	28,503	0,03508
1,40	4,0552	0,2466	3,40	29,964	0,03337
1,45	4,2631	0,2346	3,45	31,500	0,03175
1,50	4,4817	0,2231	3,50	33,115	0,03020
1,55	4,7115	0,2123	3,55	34,813	0,02872
1,60	4,9530	0,2019	3,60	36,598	0,02732
1,65	5,2070	0,1921	3,65	38,475	0,02599
1,70	5,4739	0,1827	3,70	40,447	0,02472
1,75	5,7546	0,1738	3,75	42,521	0,02352
1,80	6,0496	0,1653	3,80	44,701	0,02237
1,85	6,3598	0,1572	3,85	46,993	0,02128
1,90	6,6859	0,1496	3,90	49,402	0,02024
1,95	7,0287	0,1423	3,95	51,935	0,01925

Продолжение табл. 5

X	е*	ел	X	е*
4,00	54,598	0,01832	6,0	403,43	0,00248
4,05	57,397	0,01742	6,1	445,86	0,00224
4,10	60,340	0,01657	6,2	492,75	0,00203
4,15	63,434	0,01576	6,3	544,57	0,0р184
4,20	66,686	0,01500	6,4	601,85	0,00166
4,25	70,105	0,01426	6,5	665,14	0,001503
4,30	73,700	0,01357	6,6	735,10	0,001360
• 4,35	77,478	0,01991	6,7	812,41	0,001231
4,40	81,451	0,01228	6,8	897,85	0,001114
4,45	85,627	0,01168	6,9	992,27	0,001008
4,50	90,017	0,01111	7,0	1096,6	0,000912
4,55	94,632	0,01057	7,1	1212,2	0,000825
4,60	99,484	0,01005	7,2	1339,4	0,000747
4,65	104,58	0,00956	7,3	1480,5	0,000676
4,70	109,95	0,00910	7,4	1636,0	0,000611
4,75	115,58	0,00865	7,5	1808,0	0,000553
4,80	121,51	0,00823	7,6	1998,2	0,000500
4,85	127,74	0,00783	7,7	2208,3	0,000453
4,90	134,29	0,00745	7,8	2440,6	0,000410
4,95	141,17	0,00708	7,9	2697,3	0,000371
5,00	148,41	0,00674	8,0	2981,0	0,000335
5,05	156,02	0,00641	8,1	3294,5	0,000304
5,10	164,02	0,00610	8,2	3641,0	0,000275
5,15	172,43	0,00580	8,3	4023,9	0,000249
5,20	181,27	0,00552	8,4	4447,1	0,000225
5,25	190,57	0,00525	8,5	4914,8	0,000203
5,30	200,34	0,00499	8,6	5431,7	0,000184
5,35	210,61	0,00475	8,7	6002,9	0,000167
5,40	221,41	0,00452	8,8	6634,2	0,000151
5,45	232,76	0,00430	8,9	7332,0	0,000136
5,50	244,69	0,00409	9,0	8103,1	0,000123
5,55	257,24	0,00389	9,1	8955,3	0,000112
5,60	270,43	0,00370	9,2	9897,1	0,000101
5,65	284,29	0,00352	9,3	10938	0,000091
5,70	298,87	0,00335	9,4	12088	0,000083
5,75	314,19	0,00318	9,5	13360	0,000075
5,80	330,30	0,00303	9,6	14765	0,000068
5,85	347,23	0,00288	9,7	16318	0,000061
5,90	365,04	0,00274	9,8	18034	0,000055
5,95	383,75	0,00261	9,9	19930	0,000050
			10,0	22026	0,000045

ч

6. Греческий алфавит

А,	а	— альфа	I,	ι —йота	Р,	р-ро
В,	β	— бета	К,	κ — каппа	Σ,	σ — сигма
Г,	Y	— гамма	А,	λ — ламбда	Т,	τ—тау
Л,	δ	—дельта	М,	μ — мю	г,	υ— ипсилон
Е,	ε	— эпсилон	Ν,	V — ню	Ф,	φ — фи
Ζ,	ζ	—дзета	S,	ξ—кси	х,
Н,	η	— эта	о,	о—омикрон	ψ.	•ψ — пси
Θ,	Ό,	θ—тэта	п,	π— пи	Ω,	ω—омега

7. Некоторые постоянные числа и приближенные формулы

Постоянные числа	Приближенные формулы <при α < 1)
Jt= 3,1416	(1 ± а)п 1 ±ясх
л2 = 9,8696	еа ¢=¾* 1 +а
Vn = 1,7725	In (1 +ос) ^a
е = 2,7183	sin а ^ а
Ige = 0,4343	cos сс S=S=J 1 — а2/2
In 10=2,3026	tga^cc

I

8. Некоторые сведения о, векторах

a (b + c) = ab+ac [a, b + с] = [abj + [acj ab=axbx+aybtJ+aJbz [a [bc]] = b (ac) —с (ab) i j k [abj= ax ay az = (aybz~azby) \-Y{a^x—axbz) \ + (axby—aybx) k и** by bz
d £ , , ч dSL t dh -^-(a + b) = —+ ^ d da da. Ϊμ-Ϊ'+·Ϊ

9. Таблица производных и интегралов

Функция	Производная	Функция	Производная	Функция	Производная
Xn 1	пхп~ъ 1	sin χ COS X	COS X — sin χ	arcsin χ	1 у 1-х3
X		tg*	1	arccos χ	1
1	η		COS2X		у 1-х2
Xn		ctg X	1	arctg χ	1
V* * е* Qnx а* In χ	1		Sin3X		I+X2
	2 VJ Qx тпх ах In а 1 X				1 1+х2 ch χ sh χ 1 ch2x 1 sh2x
		VH In и и v	ur 2 Vu ut и vuf—υ' и v2	arcctg χ shx eh χ thx cth χ

C dx ,

\ s— — tg л:

J COS²JC

C dx .

χ—τ,— S=-Ct gx J sin² χ °

J г^х dx=e^x f ^dx *

Jrr^^arctg*

C dx

\

ί*

J *

J sin л; dx= — cos χ J cosx dx=Sin χ

J tg x dx = — In cos jc J сtgx dx = ln sin χ

1 = я res in χ

^T)

f _r^dx =In (X+Vtf

Интегрирование «по частямк = — Jydu

Значения некоторых определенных интегралов

OO J XnQTx dx — < О	If п=O- xJ2VlU П = 112 1, 2, д-2	OO J xnQ-x*dx = о	t (VaVrS^ « = 0 , V2- ' я=»1 I 1UVnf /г=2 I V2f « = 3
OO С хп dx	/ 2,31, /г = Va π2/6, л= 1 2,405, л =г 2 л4/15, л = 3 24,9, /г = 4	α	0,225, а=1. 1,18, а = 2 2,56, а1= 3 4,91, α = 5 6,43, α= 10
J е*-1 ~ о		3 О

10. Астрономические величины

Космическое тело	Средний радиус, м	Масса, кг	Средняя плотность, IO3 кг/м3	Период обра­щения вокруг оси, сутки
Солнце Земля Луиа	6,95. 10» 6,37. 106 1,74- 10в	1,97- Юзо 5,96. 1024 7,30. IO3*	1,41 5,52 3,30	25,4 1,00 27,3

Планеты Солнеч­ной системы	Среднее расстояние от Солнца, IO6 км	Период обращения вокруг Солнца в годах
Меркурий	57,87	0,241
Венера	108,14	0,615
Земля	149,50	1,000
Марс	227.79	1,881
Юпитер	777,8	11,862
Сатурн	1426,1	29,458
Уран	2867,7	84,013
Нептун	4494	164,79
Плутон	9508	248,43

11. Плотности веществ

Твердые вещества	р, г/см3	Жидкости	р, г/см3
Алшз	3,5	Бензол	0,88
Алюминий	2,7	Вода	1,00
Вольфрам	19,1	Глнцернн	1,26
Графит	1.6	Касторовое масло	0,90
Железо (сталь)	7,8	Керосин	0,80
Золото	19,3	Ртуть	13,6
Кадмий	8,65	Спнрт	0,79
Кобальт	8,9	Тяжелая вода	1,1
Лед	0,916	Эфир	0,72
Медь	8,9
Молибден Натрий	ν 10,2 0,97	Газы (при нормальных условиях)	р, К Г/Ma
Никель	8,9 7,4
Олово
Платина	21,5	Азот	1,25
Пробка	0,20	Аммиак	0,77
Свинец	11,3	Водород	0,09
Серебро	10,5	Воздух	1,293
Титан	4,5	Кислород	1,43
Уран	19,0	Метай	0,72
Фарфор	2,3	Углекислый газ	1,98
Цинк	7,0	Хлор	3,21

12. Коэффициенты теплового расширения

(при комнатных температурах)

Твердое тело	Коэффициент линейного расширения α, Ю-® K-*	Жидкость	Коэффициент объемного расширения β, IO"4 К"1
Алюминий Латунь Медь Сталь (железо) Стекло обычное • Примечание, а =	22,9 18,9 16,7 И 8,5 1 сU I дТ>	Вода Глицерин Керосин Ртуть Спирт этиловый 1 dV V дТ'	2 Л 5,0 10,0 1,8 11,0

13. Упругие постоянные. Предел прочности

Материал	Модуль Юнга Е, ГПа	Модуль сдвига G, ГПа	Коэффи­циент Пуассона μ	Предел прочности на разрыв iV ГПа	Коэффи­циент сжимаемости β, ГПа~*
Алюминий Медь Свинец Сталь (железо) Стекло Вода Примечание. 1	70 130 16 200 60 <оэффнцие	26 40 5,6 81 30 нт сжимае	0,34 0,34 0,44 0,29 0,25 мости β =	0,10 0,30 0,015 0,60 0,05 1 dV V dp '	0,014 0,007 0,022 0,006 0,025 0,49

14. Давление насыщенных паров воды

0C	Давление,	о	Давление,		Давление·
	кПа	U	кПа	с	кПа
0	0,61	25	3,15	60	19,9
- 5	0,87	30	4,23	70	31,0
10	1,22	35	5,60	80	47,3
15	1,70	40	7,35	90	70,0
20	2,33	50	12,3	100	101

15. Постоянные газов

(при нормальных условиях)

Газ	Относи­тельная		Тепло­провод­ность мВт κ'Μ·Κ	Вязкость	Днаметр моле­	Постоянные Ван-дер-Ваальса
	молеку­лярная масса			мкПа --с	кулы нм	атм-л2	ъ л
						моль2	V* *■ " моль
Не	4	1,63	141,5	18,9	0,20
Ar	40	1,67	16,2	22,1	0,35	1,30	0,032
H2	2	1,41	168,4	8,4	0,27	0,24	0,027
N2	28	1,40	24,3	16,7	0,37	1,35	0,039
O2	32	1,40	24,4	19,2	0,35	Г, 35	0,032
CO2	44	1,30	23,2	14,0	0,40	3,62	0,043
H2O	18	1,32	15,8	9,0	0,30	5,47	0,030
Воздух	29	1,40	24,1	17,2	0,35	—	—
Примечание. В этой таблице приведены средние значения диамет­ров молекул. При более точных расчетах следует иметь в виду, что значения A9 полученные из коэффициентов вязкости, теплопроводности, диффузии и Постоянной Ь Ван-дер-Ваальса, заметно отличаются друг от друга.

16. Постоянные жидкостей и твердых тел

(при нормальных условиях)

Вещество	Удельная теплоемкость Дж ' г. к	Удельная теплота паро­образования <7, Дж/г	Удельная теплота плавления <7, Дж/г	Поверхност­ное натяжение а, мН/м
Вода	4,18	2250		73 *
Глицерин	2,42	—	—	66
Ртуть	0,14	284	—	490
Спирт	2,42	853	—	22
Алюминий	0,90	—	321	—.
Железо	0,46	—	270	—
Лед	2,09	—	333	—
Медь	0,39	—	175	—
Серебро	0,23	—	88	—
Свинец	0,13		25

17. Диэлектрические проницаемости

(относительные)

Диэлектрик	8	Диэлектрик	8
Вода	81	Слюда	7,5
Воздух	1,00058	Спирт	26
Керосин	2,0	Стекло	6,0
Парафин	2,0	Фарфор	6>0
Плексиглас	3>5	Эбонит	2,7
Полиэтилен	2,3

18. Удельные сопротивлении проводников

Проводаик	Удельное сопротивление (при 20 0C) р, иОМ'М	Те мп ературный коэффициент а,
Алюминий	25	4,5
Вольфрам	50	4,8
Железо	90	6,5
Золото	20	4,0
Медь	16	4,3
Свинец	190	4,2
Серебро	15

19. Магнитные восприимчивости пара- и диамагнетиков

(относительные)

Парамагнетики	μ-1, 10—β	Днамагнетики	μ—1. Ю-»
Азот	0,0*13	Водород	—0,063
Воздух	0,38	Бензол	—7,5
Кислород	19	Вода	—9,0
Эбонит	14	Медь	—10,3
Алюминий	23	Стекло	—12,6
Вольфрам	176	Каменная соль	—12,6
Платина	360	Кварц	—15,1
Жидкий кислород	3400	Висмут	—176

Цвет

п,

20. Показатели преломления

Вещество	η	Вещество	η
Воздух Вода Примечан зависят от при ρ Oj приведенные в эт как условные.	1,00029 1,33 и е. Как извс 5ы вещества ой таблице зш	Стекло Алмаз истно, показатели ι и длины волны CBi ачения η следует ра	1,50 2,42 треломления ?та, поэтому осматривать

Исландский шпат

Кварц

Длина волИы λ, нм

п_г

687 красный

656 оранжевый

589 желтый

527 зеленый

486 голубой

431 сине-фиолетовый

486. 1,489 1,491 1,495 1,498

1,653 1,655 1,658 1,664 1,668 1,676 1,683

551. 1,553 1,556 1,559 1,564 1,568

400 фиолетовый

21. Вращение плоскости поляризации

Естественное вращение в кварце (толщина пластинки 1 мм)

λ, HM	φ, град	λ, HM	φ, град	λ, HM	φ, град
217,4 219,4 274,7 328,6	295,65 226,91 220,7 143,3 121,1 78,58	344,1 435,9 491,6 508,6	70,59 58,89 48,93 41,54 31,98 29,72	589,5 656,3 670,8 1040 1450 1770	21,72 17,32 16,54 6,69 3,41 2,28

Магнитное вращение (λ = 589ΗΜ). Постоянная Верде V:

Жидкость	t I > Vi угл. мни/А 1 i	Жидкость	V1 у гл. мии/А
Бензол Вода	2,59 j 0,016	Сероуглерод Спирт этиловый	0,053 1,072

22. Работа выхода электрона из металлов

Металл	А, эВ	Металл	At зВ	Металл	At SB
Алюминий	3,74	Калий	2,15	Никель	4,84
Барий	2,29	Кобальт	4,25	Платина	5,29
Висмут	4,62	Литий	2,39	Серебро	4,28
Вольфрам	4,50	Медь	4,47	Титан	3,92
Железо	4,36	Молибден	4,27	Цезий	1,89
Золото	4,58	Натрий	2,27	Цинк	3,74

M

23. Край К-полосы поглощения

Z	Элемент	Яд, пм	Z	Элемент	λ^, пм
23	V	226,8	47	Ag	48,60
26	Fe	174,1	50	Sn	42,39
27	Со	160,4	74	W	17,85
28	Ni	148,6	78	Pt	15,85
29	Cu	138,0	79	Au	15,35
30	Zn	128,4	82	Pb	14,05
42	Mo	61,9	92	U	10,75

24. Массовые коэффициенты ослабления

(рентгеновское излучение, узкий пучок)

Массовый коэффициент ослабления μ/ρ, см²/г

λ, пм

Воздух

Вода

Свииец

Медь

Алюминий

0,16 0,18 0,29 0,44 0,66 1,0 1,5 2,1 2,8 3,8 12 28 51

10 20 30 40 50 60 70 SO 90 100 150 200 250

0,16 0,28 0,47 1,1

2,0 3,4

5,1

7,4 11 15 46 102 194

0,36 1,5 4,3 9,8 19 32

48. 70 98

131

48. 108 198

9. 14 31 54 90

139

0,48 0,75 1,3 1,6 2,1 2,6 8,7 21 39

25. Потенциалы ионизации атомов

	Атом	Потенциал			Поте-ициал
Z		ионизации	Z	Атом	ионизации
		Ф» В			Ф·» в
1	H	13,59	7	N	14,54
2	Не	24,58	8	О	13,62
3	Li	5,39	9	F	17,42
4	Be	9,32	10	Ne	21,56
5	В	8,30	11	Na	5,14
6	G	11,27	80	Hg	10,44

26. Массы легких а годов

Z	Изотоп	Избыток массы атома At. — Ai а.е.м г .	Z	Изотоп	Избыток массы атома А — At а.е.м. г
0	η	0,00867	6		0,01143
1	W	0,00783		Cia	0
	H2	0,01410		C1S	0,00335
	№	0,01605	1	N13	0,00574
2	Не?	0,01603		NW	0,00307
	He4	0,00260		N1S	0,00011
3	Li0	0,01513	3	019	0,00307
	Lil	0,01601		Oie	—0,00509
4	Bei	0>01693		W	—0,00087
	Be8	0,00531	9	pie	—0,00160
	Be»	0,01219	10	Ne20	—0,00756
	Be10	№1354	11	Na^	—0,01023
5	Вю	0,01294		Na24	—0,00903
	B^	0,00930	12	Mg24	—0,01496
Примечание.		Здесь Ar — относительная атомная масса (в а. е. м.)*
А—массовое число.

27. Периоды лолураслада радиоизотолов

Z	Изотоп	Тип распада	Период полураспада
27	Кобальт Coeo	β	5,2 года
38	Стронций Sr®0	β	28 лет
84	Полоний Po2Ao	α	138 дней
86	Радон Rn222	а	3,8 дня
88	Радий Ra22e	а	1620 лет
92	Уран U2?8	а	4,5-10® лет

28. Единицы физических величин

Обозначения и названия некоторых единиц

А—ампер	дин—дина	H — ньютон
а. -е. м. — атомная единица	Дж — джоуль	П —пуаз
массы	дп—диоптрия	Па —паскаль
Б —бел	К — кельвин	рад—раднан
б—барн	кд—кандела	с—секунда
В—вольт	Кл — кулон	См —сименс
Вб— вебер	л — литр	ср —стерадиан
Вт—ватт	лк —люкс	Т—тесла
Г —генри	лм— люмен	Φ — фарада
г —грамм	м —метр	ч —час
Гс — гаусс	мин—минута	Э —эрстед
Тц—герц	Мкс—максвелл	эВ—элешроявольт