4. Определение частоты попадания предприятий в группы. Результаты в таблице 4.

Таблица 4 - таблица частот

Группы предприятий по среднегодовой стоимости основных производственных фондов	Число предприятий, ед.	Накопленные частоты
215-257	3	3
257-299	4	7
299-341	7	14
341-383	8	22
383-425	6	28
425-467	2	30

Интервал 341-383 имеет наибольшую частоту, следовательно, он является модальным.

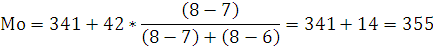
2. Мода выпуска продукции.

   1. Расчет количества групп с помощью формулы Старджесса.

n=1+3,322*lgN,

где N – объём статистической совокупности.

n=1+3,322*lg30=1+3,322*1,47712=1+4,9=5,9≈6

2. Определение ширины интервала группировки.

Интервал группировки определяем по формуле:

,

где n – число групп, X_max и X_min – максимальное и минимальное и минимальное значения суммы активов баланса.

3. Определение границ групп:

Группа 1	XН1= Xmin=175
	XВ1= XН1+i=175+50=225
Группа 2	XН2= XВ1=225
	XВ2= XН2+i=255+50=275
Группа 3	XН3= XВ2=275
	XВ3= XН3+i=275+50=325
Группа 4	XН4= XВ3=325
	XВ4= XН4+i=325+50=375
Группа 5	XН5= XВ4=375
	XВ5= XН5+i=375+50=425
Группа 6	XН6= XВ5=425
	XВ6= XН6+i=425+50=475

4. Определение частоты попадания предприятий в группы. Результаты в таблице 5.

Таблица 5 - таблица частот

Группы предприятий по выпуску продукции	Число предприятий, ед.	Накопленные частоты
175-225	2	2
225-275	4	6
275-325	9	15
325-375	8	23
375-425	4	27
425-475	3	30

Интервал 275-325 имеет наибольшую частоту, следовательно, он является модальным.

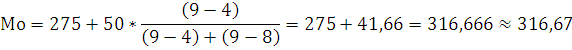
3. Вычисление медианы.

Формул вычисления медианы:

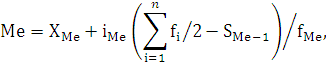
где X_Me – нижняя граница медианного интервала;

i_Me - медианный интервал;

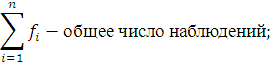
– сумма наблюдений накопленных до начала медианного интервала;

f_Me – число наблюдений в медианном интервале.

1. Вычисление медианы среднегодовой стоимости основных производственных фондов.

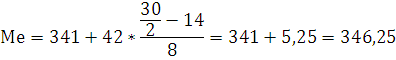
2. Вычисление медианы выпуска продукции.

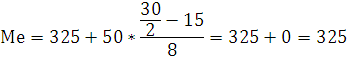
4. Вычисления размаха вариации.

Размах вариации рассчитывается по формуле:

где X_max и X_min – максимальное и минимальное значения варьирующего признака.

1. Размах вариации среднегодовой стоимости основных производственных фондов.

2. Размах вариации выпуска продукции.

5. Вычисление дисперсии.

Дисперсия вычисляется по формуле:

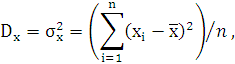
где xi - значение признака;

– среднее значение;

n – число признаков.

1. Вычисление дисперсии среднегодовой стоимости основных производственных фондов.

3534,58

2. Вычисление дисперсии выпуска продукции.

4290,63

6. Нахождение среднего квадратического отклонения.

Формула нахождения СКО:

1. Вычисление СКО среднегодовой стоимости основных производственных фондов.

2. Вычисление СКО выпуска продукции.

7. Вычисление коэффициента вариации.

Формула коэффициента вариации:

1. Вычисление коэффициента вариации среднегодовой стоимости основных производственных фондов.

2. Вычисление коэффициента вариации выпуска продукции.

3. Проверка на сколько близко полученное распределение к нормальному.

   1. Оценка степени колеблимости значений признаков в совокупности.

Степень колеблемости среднегодовой стоимости основных производственных фондов составляет σ=59,5 – колеблемость средняя.

Степень колеблимости выпуска продукции равна σ=65,5 – большая степень колеблимости.

2. Оценка степени однородности по изучаемому признаку.

Совокупность признаков среднегодовой стоимости основных производственных фондов имеет коэффициент вариации равных 17,5% , следовательно, совокупность достаточно однородна.

Совокупность признаков выпуска продукции имеет коэффициент вариации 20,08% , следовательно, совокупность достаточно однородна.

3. Оценка количества попаданий индивидуальных значений признаков в диапазоны

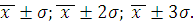
   1. Оценка количества попаданий индивидуальных значений признаков в диапазоны .

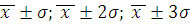Для совокупности признаков среднегодовой стоимости основных производственных фондов в диапазон попадает 66,7%, в диапазон попадает 93,3%, в диапазон попадает 100% всех единиц совокупности (таблица 5). Следовательно, данная совокупность удовлетворяет требованиям нормального распределения.

Для совокупности признаков выпуска продукции в диапазон попадает 60%, в диапазон попадает 93,3%, в диапазон 100% всех единиц совокупности (таблица 6). Следовательно, данная совокупность удовлетворяет требованиям нормального распределения.

Таблица 6 – попадание индивидуальных значений признаков в диапазоны

Для совокупности по признаку среднегодовая стоимость основных производственных фондов				Для совокупности по признаку величина выпуска продукции
	280,50	20	66,7%		260,58	18	60%
	399,50				391,58
	221,00	28	93,3%			28	93,3%
	459,00
	161,50	30	100%			30	100%
	518,50

4. Построение интервального вариационного ряда и гистограммы распределения единиц совокупности.

   1. Построение интервального вариационного ряда и гистограммы распределения для совокупности среднегодовая стоимость основных производственных фондов.

Таблица 7 – интервальный ряд распределения среднегодовой стоимости основных производственных фондов.

Интервалы групп	Число предприятий, ед.
215-257	3
257-299	4
299-341	7
341-383	8
383-425	6
425-467	2

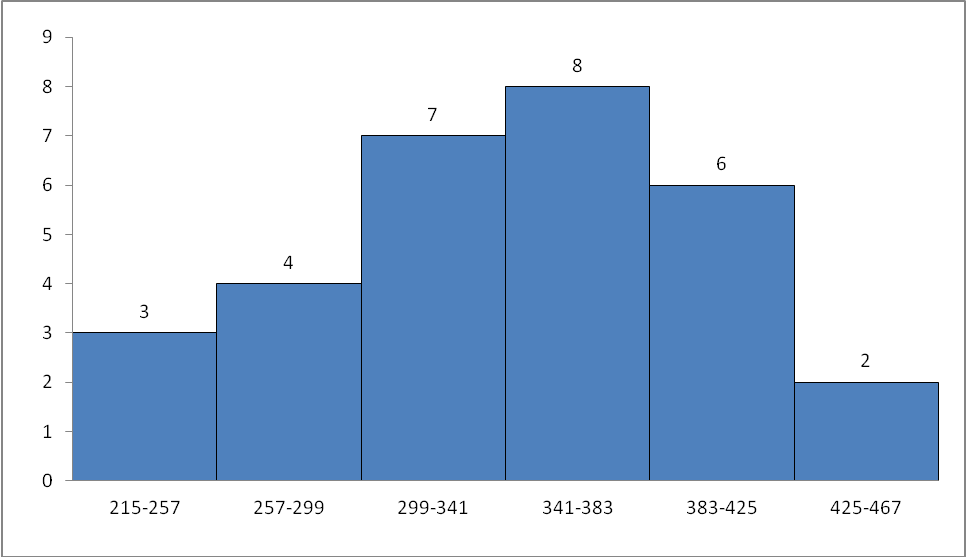
Гистограмма 1 – распределение среднегодовой стоимости основных производственных фондов.

Данное распределение является нормальным, хотя от идеальной кривой нормального распределения есть некоторые отклонения.