Затухание свободных колебаний

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Закон затухания колебаний зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Свободные затухающие колебания линейной системы описываются уравнением:

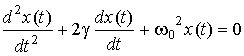, (7.1.1)

где - коэффициент затухания, - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания. Выражение коэффициента затухания через параметры системы зависит от вида колебательной системы. Например, для пружинного маятника 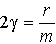где r - коэффициент сопротивления, т.е. коэффициент пропорциональности между скоростью и силой сопротивления. Для затухающих колебаний в колебательном контуре (рис.7.1.1): 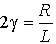, где R - величина активного сопротивления контура.

Для решения уравнения (7.1.1) производится подстановка . Эта подстановка приводит к характеристическому уравнению:

, (7.1.2)

которое имеет два корня:

, . (7.1.3)

При не слишком большом затухании (при ) подкоренное выражение будет отрицательным. Если его представить в виде , где - вещественная положительная величина, называемая циклической частотой затухающих колебаний и равная , то корни уравнения (3) запишутся в виде:

и . (7.1.4)

Общим решением уравнения (7.1.1) будет функция:

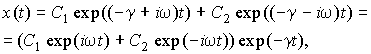(7.1.5)

которую можно представить в виде:

, (7.1.6)

З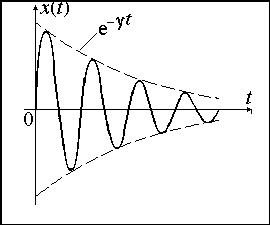 десь и - произвольные постоянные.

В соответствии с (7.1.6) движение системы можно условно рассматривать как гармоническое колебание частоты w с амплитудой, изменяющейся по закону:

. (7.1.7)

Скорость затухания колебаний определяется коэффициентом затухания . В соответствии с выражением (7.1.7) коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда колебаний уменьшается в «e»=2.718 раз. Период затухающих колебаний определяется формулой:

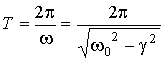. (7.1.8)

При незначительном затухании ( ) период колебаний практически равен 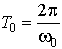. С ростом период увеличивается. Из соотношения (7.1.7) следует, что . Такое отношение амплитуд называется декрементом затухания, а его натуральный логарифм - логарифмическим декрементом затухания:

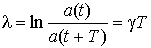. (7.1.9)

Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в «e» раз. Помимо рассмотренных величин для характеристики колебательной системы употребляется величин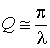а , называемая добротностью колебательной системы. Добротность пропорциональна числу колебаний, совершаемых системой за то время, за которое амплитуда колебаний уменьшается в «e» раз. Большим значениям добротности соответствует малое затухание. Энергия колебательной системы убывает со временем. Это обусловлено наличием затухания. При малом затухании, когда энергия изменяется по закону:

, (7.1.10)

где - значение энергии в начальный момент.

Можно показать, что при слабом затухании добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент времени, к убыли этой энергии за один период колебаний.

С ростом g период колебаний увеличивается. При период обращается в бесконечность, т.е. движение перестает быть периодическим. При выведенная из положения равновесия система возвращается в него, не совершая колебаний.

ДЕКРЕМЕНТ ЗАТУХАНИЯ (от лат. decrementum - уменьшение, убыль) (логарифмический декремент затухания) - количественная характеристика быстроты затухания колебаний в линейной системе; представляет собой натуральный логарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту же сторону. T. к. в линейной системе колеблющаяся величина изменяется по закону (где постоянная величина - коэф. затухания) и два последующих наиб. отклонения в одну сторону X₁ и X₂ (условно наз. "амплитудами" колебаний) разделены промежутком времени (условно наз. "периодом" колебаний), то , а Д. з. .

Так, напр., для механич. колебат. системы, состоящей из массы т, удерживаемой в положении равновесия пружиной с коэф. упругости k и испытывающей трение силой F_T, пропорциональной скорости v (F_Т =-bv, где b - коэф. пропорциональности), Д. з.

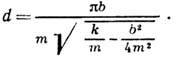
Логарифмический декремент затухания - безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.