11. Момент силы. Момент импульса материальной точки и механической системы. Закон сохранения момента импульса механической системы.

Момент силы.

Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Вопрос 13. Кинетическая энергия при поступательном и вращательном движений твердого тела.

1. Работа и кинетическая энергия

По определению, элементарной работой силы на бесконечно малом перемещении называется скалярное произведение этих двух векторов (рис. 6.1):

                .                  (6.1)

α — угол между векторами и , F_S = F × Cosα — проекция силы на направление перемещения .

Рис. 6.1

Работа силы — скалярная величина, которая может быть как положительной, так и отрицательной.

Формально знак работы определяется знаком косинуса. Если — Cosα > 0 и работа силы положительна. Сила, направленная в сторону противоположную смещению, совершает отрицательную работу. Если вектор силы образует с вектором перемещения или скорости прямой угол, то работа такой силы равна нулю. Так, работу не производит центростремительная сила при движении по круговой орбите, сила тяжести и сила реакции опоры при перемещении тела по горизонтальной поверхности.

Для того чтобы вычислить работу на конечном участке траектории, нужно рассмотреть криволинейный интеграл вектора вдоль этого участка траектории:

                          .                  (6.2)

Если в процессе движения на тело действует система сил , , …, , то работа их равнодействующей равна алгебраической сумме работ каждой силы в отдельности. Показать это несложно. Спроецируем векторное уравнение = + + … + на направление элементарного перемещения :

F_S = F_1S + F_2S + … + F_nS.

Теперь, умножив это уравнение на dS, получим искомый результат:

F_SdS = F_1SdS + F_2SdS + … + F_nSdS,

то есть:

.

Элементарная работа равнодействующей нескольких сил равна сумме элементарных работ этих сил. Это утверждение справедливо и для работ на конечном участке траектории:

.

В системе СИ работа измеряется в джоулях:

1 Дж = 1 Н × 1 м.

Работа, выполняемая в единицу времени, называется мощностью:

.

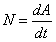Мощность — важная характеристика любого механизма. Единицей мощности является 1 Ватт. Это мощность устройства, которое ежесекундно совершает работу 1 Дж:

1 Вт = .

Теперь обратимся к теореме о кинетической энергии. Работа силы при перемещении материальной точки равна изменению кинетической энергии этой точки. Докажем это положение.

Материальная точка массы m движется под действием силы . Вычислим работу силы на участке 1-2 траектории.

                          .             (6.3)

Здесь мы воспользовались определением вектора силы и кинематическим уравнением движения .

Будем считать, что масса частицы в процессе движения не меняется, тогда:

.

Воспользуемся этим результатом в уравнении (6.3):

                     .             (6.4)

Теперь проделаем следующее очевидное преобразование: так как V² = , то 2VdV = или = VdV.

Используя это равенство в уравнении (6.4), получим окончательный результат:

                .             (6.5)

Величина = Е_к называется кинетической энергией материальной точки.

Уравнение (6.5) является математической записью теоремы о кинетической энергии: работа силы, действующей на материальную точку, равна изменению её кинетической энергии.

Важность и смысл введения понятия «работа силы» объясняется именно тем, что работа связана с изменением кинетической энергии тела:

           .                  (6.6)

Кинетическая энергия системы тел принимается равной сумме кинетических энергий всех элементов системы.

Теорема о кинетической энергии остаётся справедливой и для случая системы тел: работа всех сил, действующих на систему материальных тел, равна изменению кинетической энергии этой системы.

Здесь важно подчеркнуть, что речь идёт о работе не только внешних сил, но и внутренних, то есть сил взаимодействия элементов системы друг с другом.

Теорема Кёнига: скорость частицы и её кинетическая энергия зависят от системы отсчёта, в которой рассматривается движение частицы.

В теореме Кёнига устанавливается правило преобразования кинетической энергии при переходе из одной системы отсчёта в другую.

Рассмотрим сначала одну частицу. Пусть её кинетическая энергия в системе отсчёта S равна Е_к. Какова будет её энергия в системе отсчёта S’, движущейся со скоростью относительно S? Скорости частицы в этих двух системах связаны известным соотношением (смотри преобразования Галилея):

.

Возведём это равенство в квадрат

и домножим на

Таким образом, устанавливается связь кинетических энергий частицы в разных системах отсчёта:

                     .                  (6.7)

Обобщим этот результат на произвольную систему n материальных точек.

Для каждой частицы системы можно записать уравнение (6.7). Теперь сложим все эти уравнения:

                .             (6.8)

Здесь:     = К — кинетическая энергия системы материальных точек в системе отсчёта S.

      = — кинетическая энергия той же системы в системе отсчёта S’.

      = = , где М = — масса системы.

      = = = ,

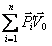где — скорость центра масс системы материальных точек в системе отсчёта S’.

Таким образом, уравнению (6.8) можно придать такой вид:

                    К= + + .                  (6.9)

Если движущуюся систему отсчёта S’ связать с центром масс, то в такой системе = 0. Формула теоремы Кёнига в этом случае упрощается:

                   (6.10)

Подводя итог, сформулируем теорему Кёнига. Кинетическая энергия системы материальных точек равна сумме кинетической энергии всей системы, мысленно сосредоточенной в её центре масс и движущейся вместе с ним и кинетической энергии той же системы в её относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс. Кинетическая энергия вращающегося тела

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить: