2.2.4. Модифицированный метод Ньютона

Рассмотренный в разд. 2.2.3 метод Ньютона требует вычисления производной на каждом шаге решения (итерации). В некоторых случаях это может существенно снизить эффективность метода в смысле затрат вычислительных ресурсов. Поэтому в тех случаях, когда вычисление производной сопряжено с существенными затратами вычислительных ресурсов, используют модифицированный метод Ньютона, в котором производная вычисляется только в точке начального приближения :

, .

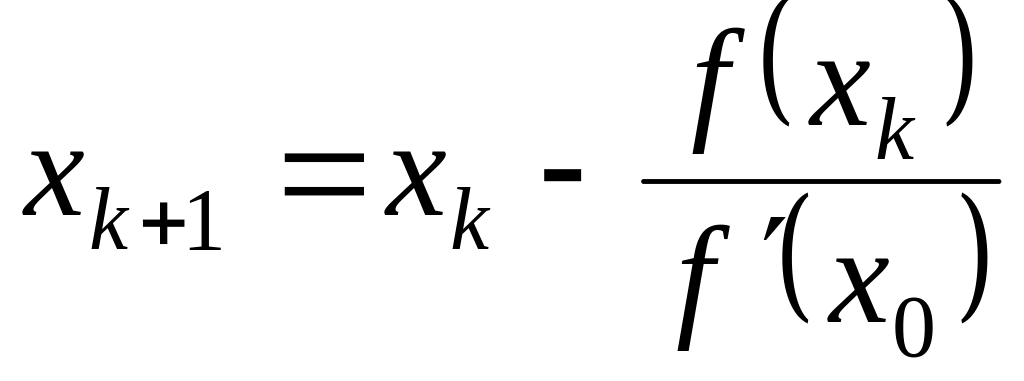Все последующие прямые, после касательной, проведенной к графику функции в точке , будут параллельны ей, поэтому представленная модификация метода Ньютона фактически реализует параллельное смещение касательной из точки начального приближения в направлении корня уравнения. В остальных аспектах модифицированный метод Ньютона аналогичен исходному методу, рассмотренному в разд. 2.2.3.

2.2.5. Метод секущих

Еще одна модификация метода Ньютона основана на математическом смысле производной и связана с приближенным вычислением производной в окрестности точки по формуле

.

Подставляя данное выражение в формулу (2.7), приходим к формуле

, , (2.9)

метода секущих. Название метода связано с его геометрической интерпретацией (рис. 2.11). Секущая, проведенная через точки и , пересекает ось абсцисс в точке , значение которой определяется формулой (2.9).

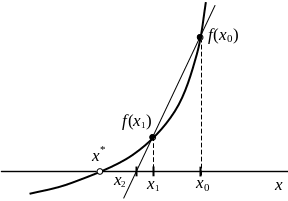
Рис. 2.11. Иллюстрация метода секущих.

Для того чтобы начать итерационный процесс в методе секущих, необходимо задать два начальных приближения: нулевое и первое . На практике, как правило, поступают следующим образом: нулевое приближение выбирают так же как в методе Ньютона, а в качестве первого приближения выбирают величину или , где – заданная точность вычисления корня. Эти значения используются для нахождения последующего (второго) приближения по формуле (2.9). Затем значения и используют для определения третьего приближения и т. д. Для завершения итерационного процесса можно воспользоваться условием (2.6).

Метод секущих уступает методу Ньютона в скорости сходимости, однако он не требует вычисления производной в явном виде, и поэтому оказывается особенно полезным в тех случаях, когда получение аналитического выражения для производной затруднено или невозможно, например, если функция получена в ходе численных расчетов, а не задана аналитически.

По алгоритму метод секущих близок к методу хорд, однако для него начальные приближения могут располагаться как с разных сторон от корня, так и с одной стороны от него. Кроме того, при уточнении корня не требуется проверять знаки функции на концах отрезка его локализации.

2.2.6. Метод итераций

Одним из наиболее важных способов численного решения нелинейных уравнений является метод итераций, частным случаем которого является и метод Ньютона. Пусть дано уравнение , где – непрерывная функция, и требуется определить его вещественные корни. Представим исходное уравнение в виде, который далее будем называть итерационной формой

. (2.10)

Искомый корень при его подстановке в уравнение (2.10) обращает последнее в тождество. Пусть известно начальное приближение к корню ( ), подставив его в правую часть уравнения (2.10) получим новое приближение , затем аналогичным образом получим и т. д.,

, . (2.11)

При определенных свойствах функции определяемая по формуле (2.11) последовательность сходится к корню уравнения .

Теорема 2.1. Если функция непрерывна, а последовательность является сходящейся, то есть существует предел , то предел данной последовательности является корнем уравнения .

Доказательство. Пусть , перейдем к пределу в равенстве (2.11):

или .

Таким образом, предел последовательности при является корнем уравнения и может быть вычислен по формуле (2.11) с любой наперед заданной точностью.

Для практического применения метода итераций требуется установить достаточные условия сходимости данного итерационного процесса.

Теорема. Пусть функция определена и дифференцируема на отрезке , причем все ее значения , то есть область определения функции совпадает с областью ее значений. Тогда, если существует число , , такое что при , то:

1. Итерационный процесс (2.11) сходится независимо от начального значения .

2. Предельное значение является единственным корнем уравнения на отрезке .

3. Числом можно cчитать наименьшее значение 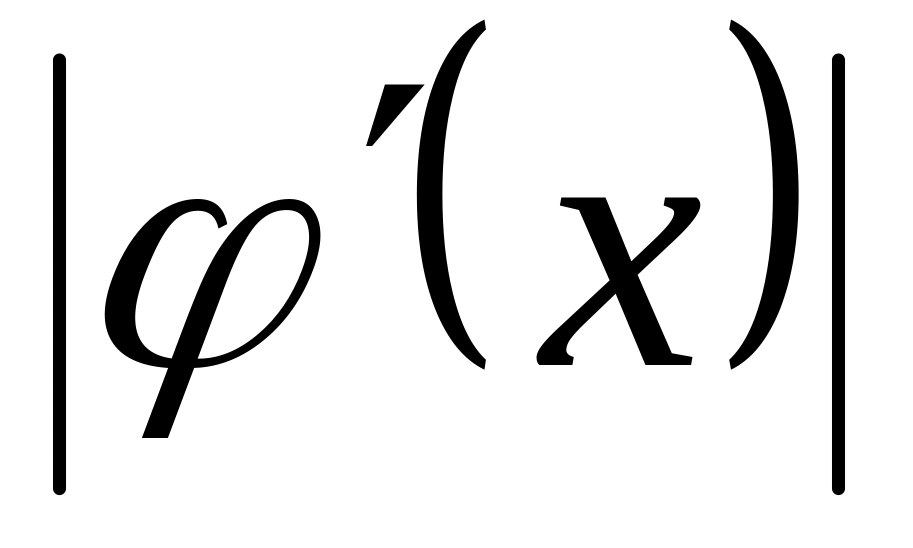на отрезке .

Замечание. Теорема остается верной, если функция определена и дифференцируема на бесконечном интервале , причем при выполнено неравенство .

Замечание. По условиям сформулированной теоремы метод итераций сходится при любом выборе начального значения на отрезке . Благодаря этому он является самоисправляющимся, т.е. отдельная ошибка в вычислениях, не выводящая за пределы отрезка , не повлияет на конечный результат, так как ошибочное значение можно рассматривать как новое начальное значение . Это свойство делает метод итераций одним из надежнейших методов решения нелинейных уравнений.

Процесс получения приближений в методе итераций проиллюстрирован на рис. 2.12. Из графиков видно, что при и при возможны как сходящиеся, так и расходящиеся итерационные процессы. Скорость сходимости зависит от абсолютной величины производной : чем меньше ее значение вблизи корня, тем быстрее сходится итерационный процесс.

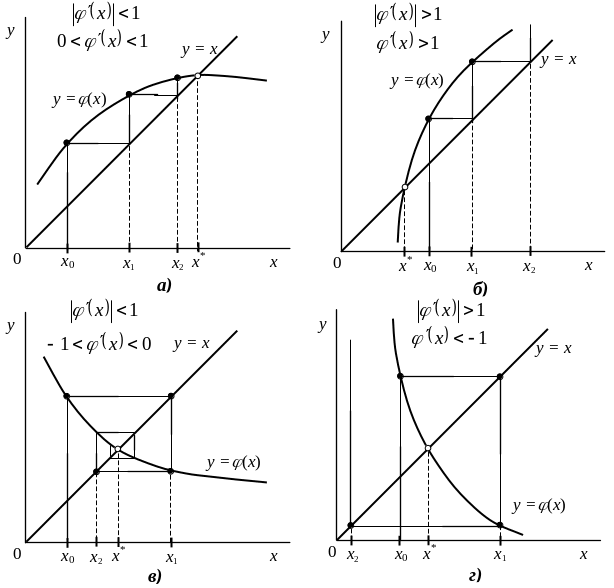
Рис. 2.12. Метод итераций: а) односторонний сходящийся процесс;