Тема 2. Ду высших порядков.
ДУ высших порядков. Основные понятия.
1.ДУ n-ого порядка могут иметь вид
Или
2.Решением уравнения
(1) или (2) называется функция
,
n
раз дифференцируемая и обращающая
уравнение (1) или (2) в тождество. Решение
может быть записано в также в неявном
виде:
и в параметрической форме:
.
График решения называется
интегральной кривой.
3.Задача Коши для уравнения (1) или (2) ставится найти решение уравнения (1) или (2), удовлетворяющее начальным условиям:
4.Наряду с задачей Коши , где все условия задаются в одной точке, для уравнений n-ого порядка можно ставить и граничные задачи и смешанные задачи, когда условия задаются на концах заданного интервала, и в некоторый момент времени (всего должно быть задано n условий).
Пример 1. Найти
решение граничной (краевой) задачи
,
удовлетворяющее граничным условиям
.
Пример 2. Найти
решения смешанной задачи для уравнения
,
удовлетворяющее начальным условиям
и граничным условиям
.
5.Функция
называется общим
решением уравнения (1) или (2) если
а) она имеет непрерывные производные до n-го порядка включительно и удовлетворяет уравнению (1) или (2),
б) система уравнений
разрешима относительно постоянных С1, С2, … , Сn.
в) при любом фиксированном наборе С1, С2, … , Сn мы получим частное решение.
Если общее решение
записано в виде
,
то оно называется общим интегралом.
6. Для уравнений (1) и (2) аналогичным образом формируется теорема Пикара.
7. Решение уравнения n-го порядка называется частным, если в каждой его точке сохраняется единственность решения задачи Коши.
8. Решение называется особым, если в каждой его точке нарушается единственность решения задачи Коши.
9. Задача интегрирования уравнения n-го порядка решается методом понижения порядка.
ДУ интегрируемые в элементарных функциях.
I
а)
Последовательно интегрируя n раз, найдем
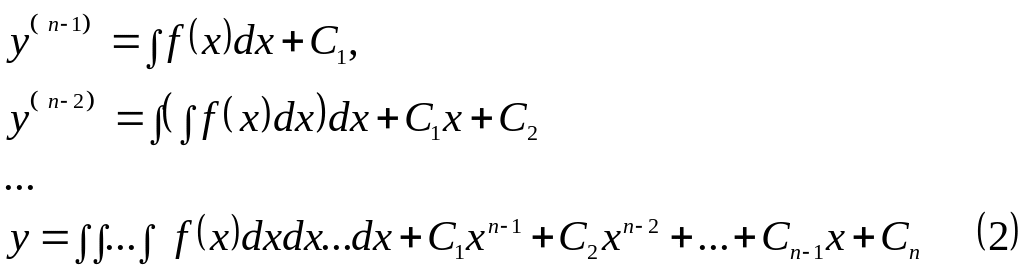
Формула (2) дает общее решение уравнения (1).
б)
Если уравнение
(3) удастся разрешить относительно
, то получим
уравнение вида (1). Пусть (3) не разрешимо
относительно
.
Введем параметр t
по формулам:
,
так, чтобы
.
Из равенства
,
найдем
или
Аналогичным образом из системы
Найдем
и т.д.
В результате найдем
общее решение в параметрической форме:
Пример 1.
.
Решение.
,
тогда
и т.д.
II
а)
Запомним замену
.
Получим уравнение
.
Решая его, найдем
.
Если это соотношение разрешимо относительно z, то получим уравнение вида (1). Если не разрешимо, то уравнение вида (3).
Пример 2.
б)
Введем параметр
t
по формулам
так, что бы
,
т.к.
,
то
и
.
В результате получим систему соотношений
которая рассматривается так же как в
пункте I
б).
Пример 3.
.
III а)
После подстановки
и умножения на
обоих частей полученного уравнения,
получим
Это уравнение можно записать в виде
Отсюда
или
,
где
Тогда уравнение
,
есть уравнение вида
.
Пример 4.
.
б)
Вводим параметр
t
по формулам
,
так что бы
.
Из равенств
.
Найдем
или
или
Это уравнение рассмотрено в пункте II б).
Мы показали, что рассмотренные 6 видов уравнений n-го порядка всегда интегрируются в элементарные функции.
ДУ допускающие понижение порядка.
I.ДУ, не содержащие явно искомой функции и нескольких первых производных:
После замены
получаем уравнение
Которое вообще говоря не всегда разрешимо. Предположим, что его удалось разрешить:
т.е.
Уравнение (3) мы рассмотрели ранее.
Пример 1.
.
Решение. Обозначим
.
Тогда
.
Сделаем замену
.
Тогда
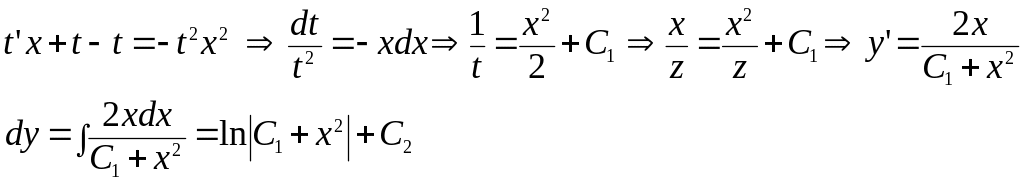
II.
Положим
.
В качестве независимой переменной будем
считать у.
Тогда
и т.д. В результате получим уравнение
Если удается его проинтегрировать, то его общий интеграл
дает ДУ первого порядка, которое всегда интегрируется.
Пример 2.
.
III.ДУ, левая часть которых является точкой производной.
Пусть левая часть уравнения есть производная некоторой функции, т.е. уравнение
можно записать в виде
общий интеграл этого уравнения
есть ДУ (n-1) порядка.
Пример 3.
.