
Тема 1. Ду первого порядка.
III. ОДУ 1-го порядка может быть записано в одной из следующих форм.
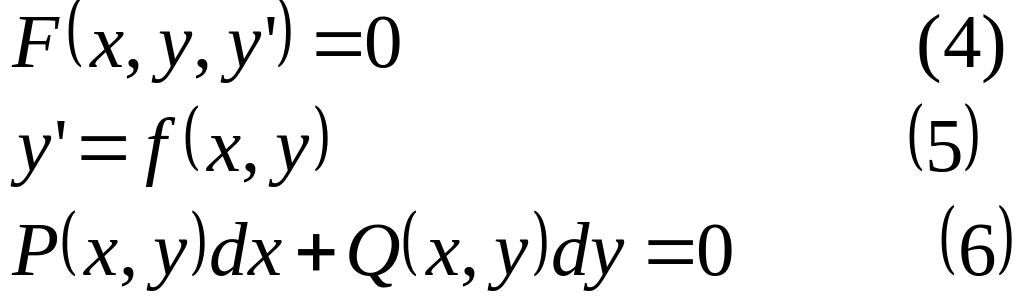
Наиболее удобной
формой является форма (5), где
![]() предполагается непрерывной и однозначной
в своей области определения В.
предполагается непрерывной и однозначной
в своей области определения В.
Решением уравнения
(5) в интервале (а,б)
называется функция
![]() ,
непрерывно-дифференцируемая в (а,б)
и образующая уравнение (5) в тождество.
,
непрерывно-дифференцируемая в (а,б)
и образующая уравнение (5) в тождество.
Общее решение ОДУ (5) будет содержать одну произвольную постоянную С и, следовательно, может быть записано в одной из трех форм:
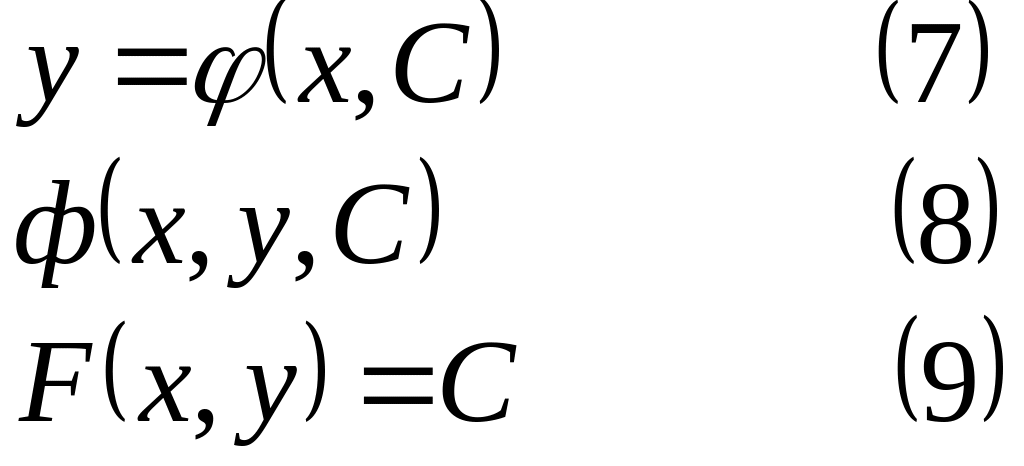
общее решение, записанное в виде (8) и (9) принято называть общим интегралом.
Если в уравнении
(5) функция
стремится к
![]() ,
то наряду с уравнением (5) надо рассмотреть
и уравнение
,
то наряду с уравнением (5) надо рассмотреть
и уравнение
![]()
Решением уравнения (5) считают такие решения уравнения (5’). Если конечно в области В и ≠0, то уравнения (5) и (5’) равносильные.
Пример 8.
![]() .
.
Легко проверить,
что функция
![]() является решением данного уравнения,
т.к.
является решением данного уравнения,
т.к.
![]() при
при
![]() ,
то наряду с данным уравнением рассмотрим
уравнение
,
то наряду с данным уравнением рассмотрим
уравнение
![]() .
Видим, что
.
Видим, что
![]() также является решением уравнения.
Поэтому полное решение уравнения
записывается в виде совокупности решений
,
.
также является решением уравнения.
Поэтому полное решение уравнения
записывается в виде совокупности решений
,
.
IV. По данному общему решению можно восстановить само ОДУ, для которого последнее будет решением. Чтобы сделать это, надо продифференцировать общее решение ОДУ n-го порядка n-раз по x, записать систему из полученных соотношений и самого решения, а затем исключить произвольные постоянные С1, С2, … , Сn из этой системы.
Пример 9. Восстановить
ДУ по его общему решению
![]() .
.
Решение. Составим систему
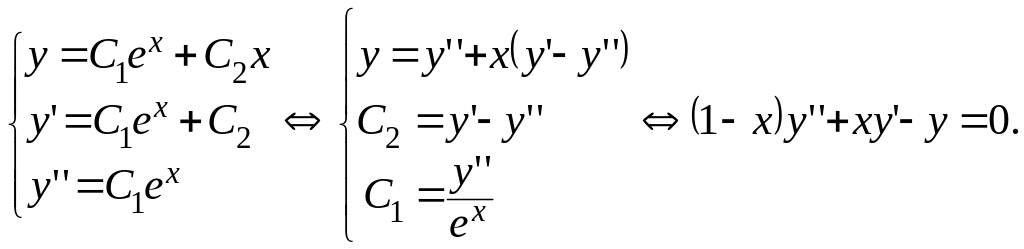
Поле направлений.
Рассмотрим геометрическую интерпретацию ДУ
![]()
и его решения.
Будем рассматривать переменные x и y как координаты точек плоскости. Вспоминая геометрический смысл производной y’, можно сказать что уравнение (1) определяет в каждой точке (x0,y0). Иначе говоря, уравнение (1) задает в каждой точке (x0,y0) направление, т.е. задает поле направлений. Если провести в поле направлений кривую, которая в каждой своей точке имеет направление совпадающее с полем направления, то как раз и получим интегральную кривую (график решения).
Из сказанного следует способ геометрического решения ДУ (1): сначала надо построить поле направлений, т.е. в каждой точке области В определить направление. Очень удобно при этом строить изоклины, т.е. линии, в точках которой поле имеет одинаковое направление. Затем проводится кривая, проходящая через точки изоклин.
Пример. Построить
интегральные кривые уравнения
![]() .
.
Решение. Построим изоклины.
Если
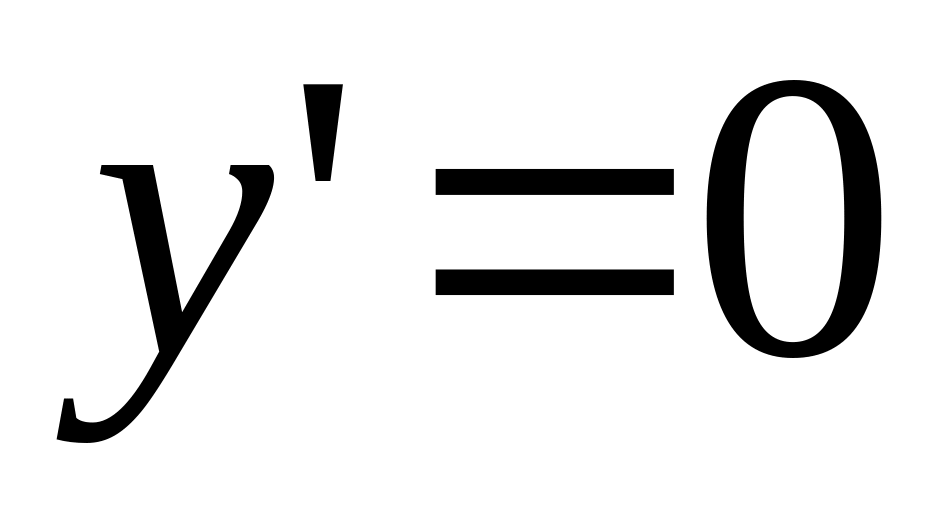 ,
т.е.
,
т.е.
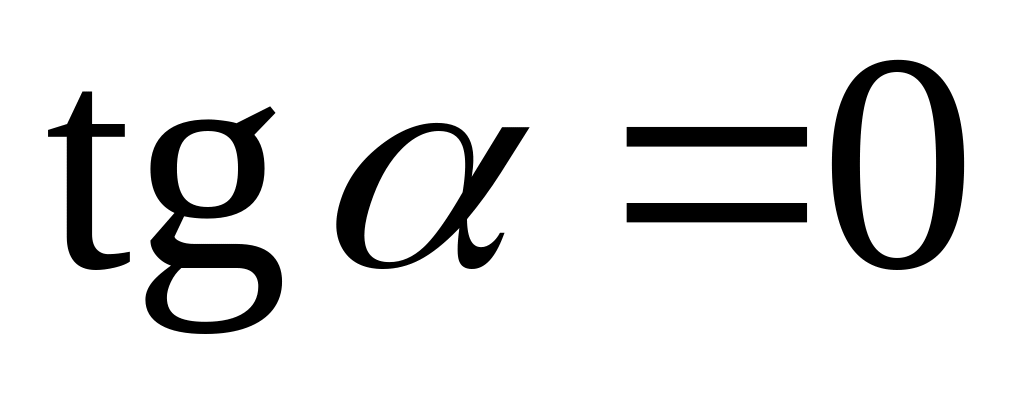 ,
то
,
то
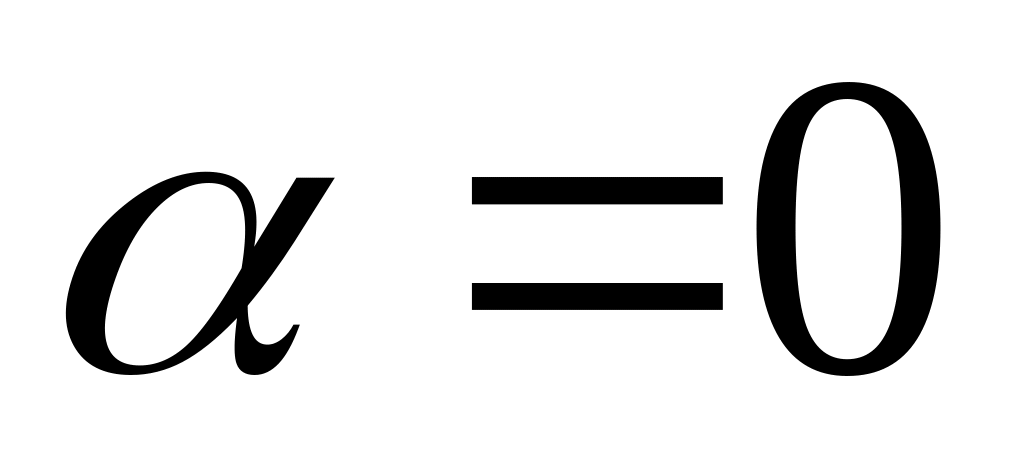 и
и
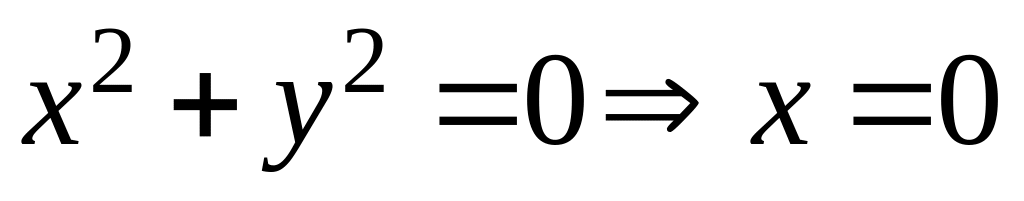 ;
;Если
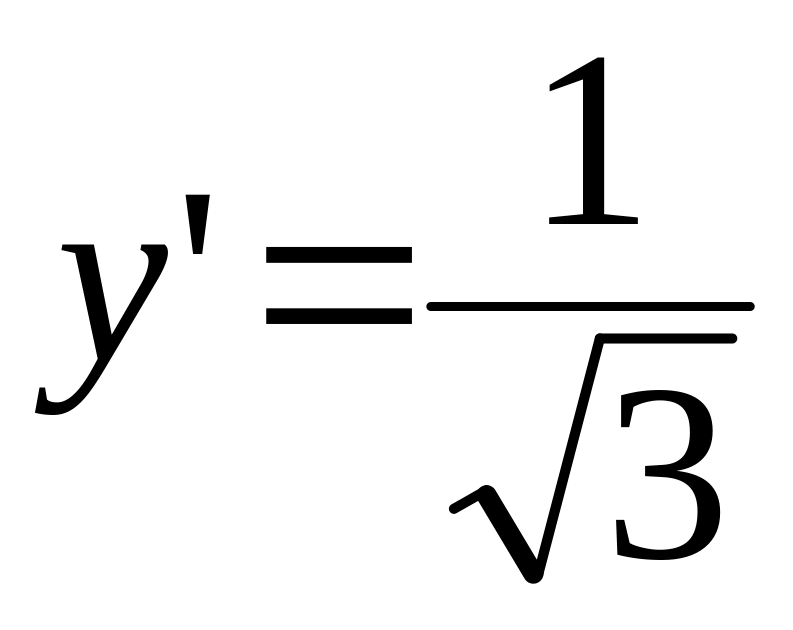 ,
т.е.
,
т.е.
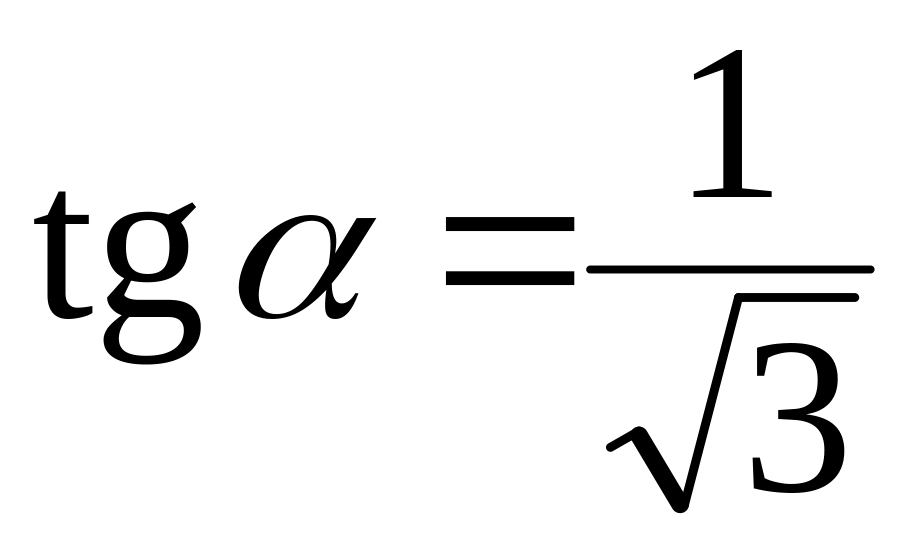 ,
то
,
то
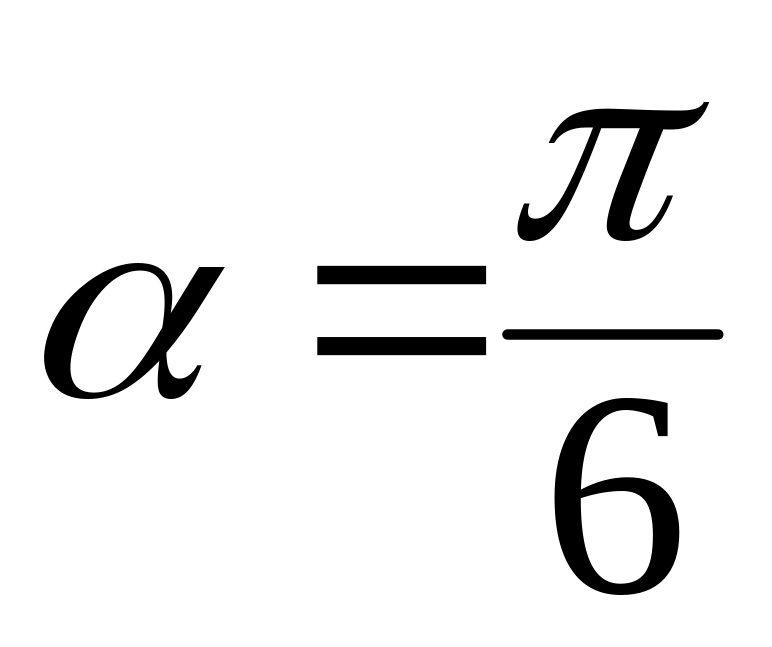 и
и
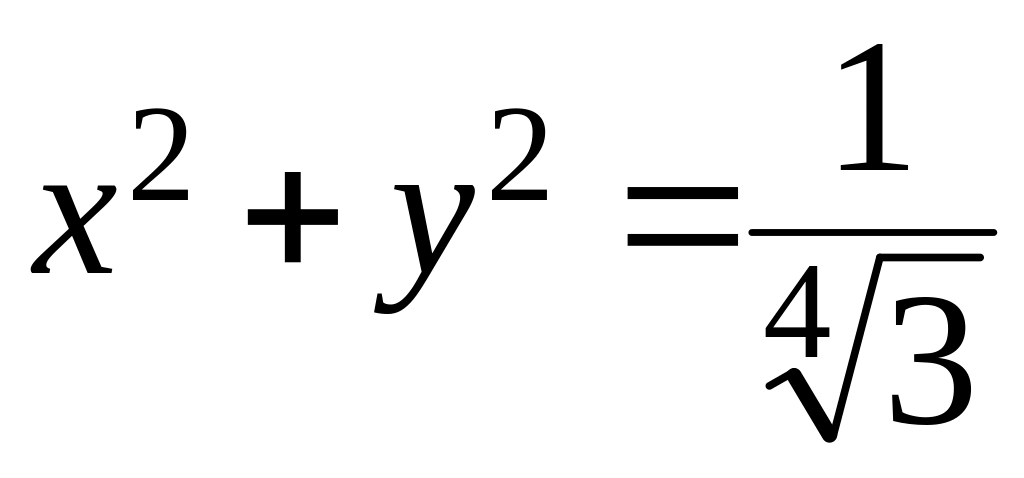
Изоклиной является окружность . В точках этой изоклины поле имеет направление . На окружности рисуем стрелки под углом к оси Ox.
3.
![]() и
и
![]() .
.
На изоклине
рисуем стрелки под углом
![]() .
.
4.
![]() и
и
![]() .
.
На изоклине
рисуем стрелочки под углом
![]() .
.
Чтобы начертить
интегральную кривую надо взять точку
![]() и провести через нее кривую так, что бы
она в каждой своей точке имела направление
совпадающее с направлением поля.
и провести через нее кривую так, что бы
она в каждой своей точке имела направление
совпадающее с направлением поля.
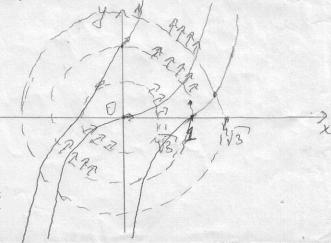
Начальные условия задачи Коши.
Как мы отметили ранее, уравнение
![]()
имеет общее решение которое можно записать в виде
![]()
графиком этого
общего решения является целое семейство
интегральных кривых. Однако очень часто
нам требуется найти не все семейство
интегральных кривых, а лишь одну
интегральную кривую, проходящую через
данную точку
.
Подставляя эту точку в соотношение (2),
найдем
![]() .
Тогда уравнение интегральной кривой,
проходящей через
запишется так:
.
Тогда уравнение интегральной кривой,
проходящей через
запишется так:
![]() .
.
Функция (3) называется
частным решением уравнения (1),
удовлетворяющим начальному условию
![]() ,
а задача отыскания частного решения
называется задачей Коши.
,
а задача отыскания частного решения
называется задачей Коши.
Дадим более строгое определение общего решения.
Определение 1. Решение (2) ДУ(1) называется общим, если:
оно разрешимо относительно С;
при всех значениях С формула (2) дает частные решения.
Пример 1. Решить задачу Коши: найти решение уравнения:
![]() ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию
![]() .
.
Решение. Общее
уравнение имеет вид
.
Начальное условие дает нам
![]() .
Тогда
.
Тогда
![]() - частное решение.
- частное решение.

Всегда ли уравнение (1) имеет решение задачи Коши, а если имеет единственно ли оно? Ответы на эти вопросы дают теоремы Пеано и Пикара, которые мы запишем здесь в упрощенной формулировке.
Теорема Пиано (теорема существования решения задачи Коши).
Если правая часть уравнения (1) определена и непрерывна в области В, то через каждую точку области В проходит по крайней мере одна интегральная кривая.
Теорема Пикара (теорема существования и единственности решения задачи Коши).
Если правая часть
уравнения (1) определена в области В,
непрерывна в ней и имеет непрерывную
частную производную
![]() ,
то через каждую точку области В
проходит одна и только одна интегральная
кривая (т.е. существует единственное
решение задачи Коши).
,
то через каждую точку области В
проходит одна и только одна интегральная
кривая (т.е. существует единственное
решение задачи Коши).
Из теорем Пеано и Пикара следует, что уравнение (1) может иметь решения, которые в каждой своей точке обладают свойством единственности решения, а так же решения, не обладающие свойством единственности.
Определение 2. Решение называется частным решением ДУ(1), если в каждой его точке сохраняется единственность решения задачи Коши.
Если решение получается из общего решения (2) при фиксированном С, то оно всегда частное. Но не всякое частное решение получается из общего.
Пример 2. Решить
уравнение
![]() .
.
Решение. Можно
проверить, что
![]() - решение. Т.к. это решение содержит
произвольную постоянную С,
то это общее решение. Если
,
то правая часть уравнения терпит разрыв.
Поэтому наряду с этим уравнением
рассматриваем уравнение
- решение. Т.к. это решение содержит
произвольную постоянную С,
то это общее решение. Если
,
то правая часть уравнения терпит разрыв.
Поэтому наряду с этим уравнением
рассматриваем уравнение
![]() .
Проверкой убеждаемся, что
также является решением уравнения.
Через каждую точку прямой
(см. рис. 2) проходит только одна интегральная
кривая – сама прямая
- частное. Оно не получается из общего
решения ни при каком С.
.
Проверкой убеждаемся, что
также является решением уравнения.
Через каждую точку прямой
(см. рис. 2) проходит только одна интегральная
кривая – сама прямая
- частное. Оно не получается из общего
решения ни при каком С.
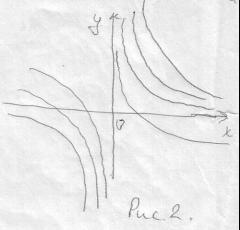
Определение 3. Решение , в каждой своей точке которого нарушается свойство единственности, называется особым.
Особое решение не получается из общего.
Пример 3. Решить
уравнение
![]() .
.
Решение.
![]() - общее решение.
- общее решение.
При x=1
правая часть
![]() терпит разрыв. Поэтому мы должны
рассмотреть так же «перевернутое»
уравнение
терпит разрыв. Поэтому мы должны
рассмотреть так же «перевернутое»
уравнение
![]() .
Легко видеть, что x
=1 – решение
уравнения. В каждой точке решение x
=1 свойству единственности решения не
удовлетворяет, следовательно x=1
– особое решение.
.
Легко видеть, что x
=1 – решение
уравнения. В каждой точке решение x
=1 свойству единственности решения не
удовлетворяет, следовательно x=1
– особое решение.
Замечание.
В дальнейшем будут встречаться следующие формулировки при рассмотрении ДУ:
1. найти общее решение;
2. найти частное
решение, удовлетворяющее условию
![]() ;
;
3. решить уравнение.
Первая формулировка будет означать, что надо найти именно общее решение. При этом не требуется отыскивать частные решения и особые решения. Вторая формулировка означает, что надо в общем решении подобрать постоянную С так, чтобы выполнялось начальное условие. Третья формулировка означает, что надо найти все возможные решения, включая частные и особые.
ДУ с разделяющимися переменными.
а) ДУ с разделенными переменными.
ДУ вида
![]() (1)
(1)
Называются
уравнениями с разделенными переменными.
Будем считать функции
![]() и
и
![]() непрерывными. Пусть
непрерывными. Пусть
![]() - решение уравнения (1). Подставляя
в (1) получим тождество, которое после
интегрирования примет вид
- решение уравнения (1). Подставляя
в (1) получим тождество, которое после
интегрирования примет вид
![]() (2)
(2)
Уравнение (2) есть в общем случае алгебраическое уравнение.
Уравнения (1) и (2) равносильны: каждое решение уравнения (1) является решением уравнения (2) и наоборот.
Определение.
Уравнение
![]() ,
которое определяет решение
,
которое определяет решение
![]() ДУ(1) как неправильную функцию, называется
общим интегралом ДУ(1).
ДУ(1) как неправильную функцию, называется
общим интегралом ДУ(1).
Т.е. формула (2) есть общий интеграл ДУ(1).
Найдя из уравнения (2) функцию , мы найдем общее решение.
Если требуется найти частное решение, удовлетворяющее начальному условию , то общий интеграл надо записать в виде
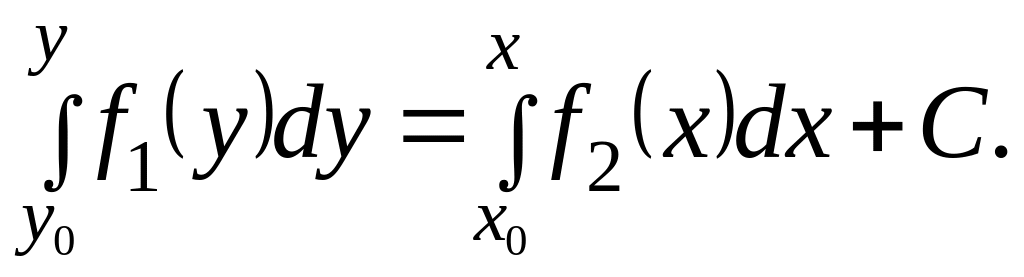
Подставляя начальные уравнения в это уравнение, найдем С=0. В результате частное решение определится из уравнения
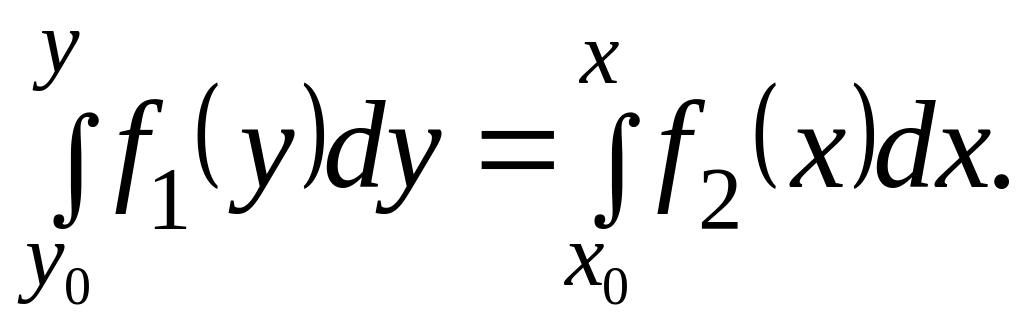
Это уравнению называют частным интегралом.
Пример 1. Решить
уравнение
![]() .
.
Решение. Интегрируя это уравнение, найдем общий интеграл
![]() .
.
Решив это уравнение,
получим общее решение:
![]() .
.
Замечание 1. В большинстве случаев формулировка «найти общее решение» может пониматься как «найти общий интеграл».
б) ДУ с разделяющимися переменными
ДУ вида
![]() (3)
(3)
называется ДУ с разделяющимися переменными.
Здесь функции
![]() могут быть как непрерывными, так и
разрывными.
могут быть как непрерывными, так и
разрывными.
Разделив ДУ(3) на производные , получим ДУ с разделенными переменными

при этом мы можем потерять решения, которые обращают в 0 производные .
Если функции терпят разрыв, то наряду с уравнением (4) следует рассмотреть и перевернутое уравнение
![]() .
.
Пример 2. Решить
уравнение
![]() .
.
Решение. Функция
![]() терпит разрыв при
.
Разделим переменные
терпит разрыв при
.
Разделим переменные
![]()
Интегрируя, найдем
![]() или
или
![]() - общее решение. Проверим являются ли
функции
и
- общее решение. Проверим являются ли
функции
и
![]() решениями. Для этого подставим их в
уравнение
решениями. Для этого подставим их в
уравнение
![]()
очевидно, что и решения. Т.к. они не содержат произвольной постоянной С, то это частные или особые решения. Графическим способом убедимся, что и - частные решения. Точка (0,0) – особая.
в) ДУ, приводящиеся к ДУ с разделяющимися переменными.
Уравнения с правой
частью вида
![]() после введения новой функции
после введения новой функции
![]() станет уравнением с разделяющимися
переменными. Действительно, получим
станет уравнением с разделяющимися
переменными. Действительно, получим
![]()
отсюда
![]() - уравнение с
разделенными переменными.
- уравнение с
разделенными переменными.
Однородные уравнения
Определение 1. Функция называется однородной функцией измерения К, если
![]() .
.
Пример 1.
![]() - однородная функция измерения m+n.
Действительно,
- однородная функция измерения m+n.
Действительно,
![]() .
.
Пример 2.
![]() - однородная функция 0 измерения, т.к.
- однородная функция 0 измерения, т.к.
![]() .
.
Определение 2. ДУ
![]()
Называется однородным уравнением, если однородная функция нулевого измерения.
ДУ(1) можно записать в таком виде
![]()
где
![]() и
и
![]() однородные функции одного и того же а
также в виде
однородные функции одного и того же а
также в виде
![]()
Определение 2’. ДУ(1) называется однородным уравнением если его можно записать в виде (3).
Вид первой части
уравнения (3) наталкивает на подстановку
![]() .
Тогда
.
Тогда
![]() и уравнение (3) примет вид
и уравнение (3) примет вид
![]()
ДУ(4) есть уравнение с разделяющимися переменными.
Пример 3.
![]() .
.
Решение.
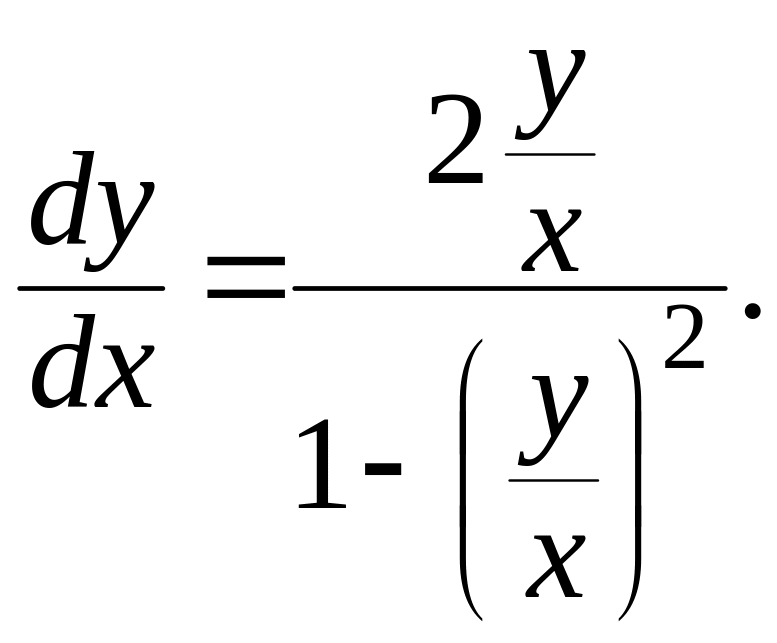
![]()
![]()
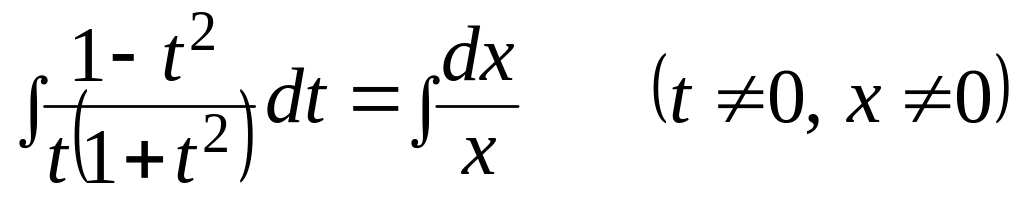
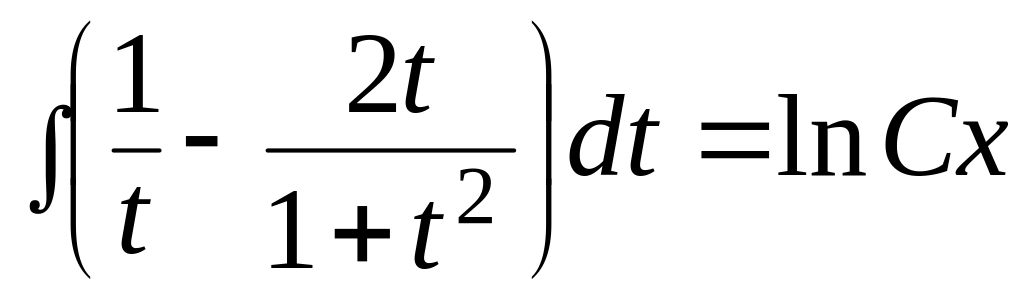
![]() - общий интеграл
в новых переменных
- общий интеграл
в новых переменных
![]() - общий интеграл
в старых переменных.
- общий интеграл
в старых переменных.
Проверкой убеждаемся, что y=0 – частное решение.
ДУ сводящиеся к однородным уравнениям.
Рассмотрим уравнение
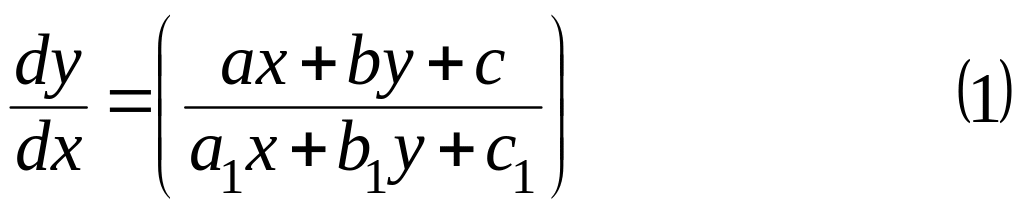
1) если
![]() ,
то
,
то
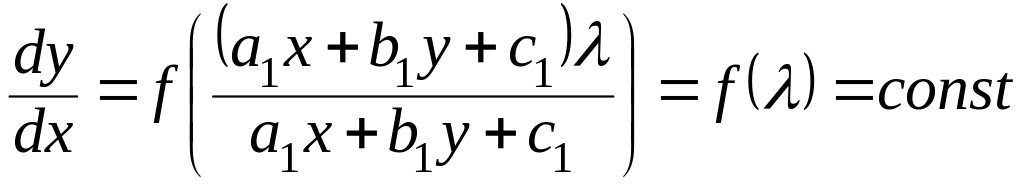 и ДУ(1) имеет решение
и ДУ(1) имеет решение
![]() .
.
2) если
![]() ,
то
,
то
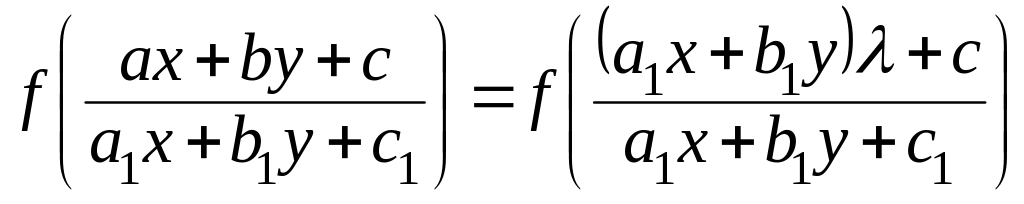 .
.
Введем новую
функцию
![]() .
Тогда
.
Тогда
![]() ,
,
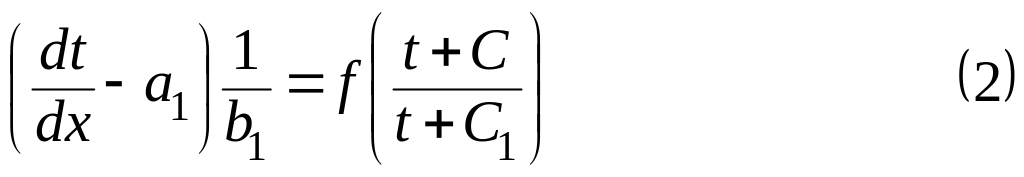
ДУ (2) есть уравнение с разделяющимися переменными.
Пусть
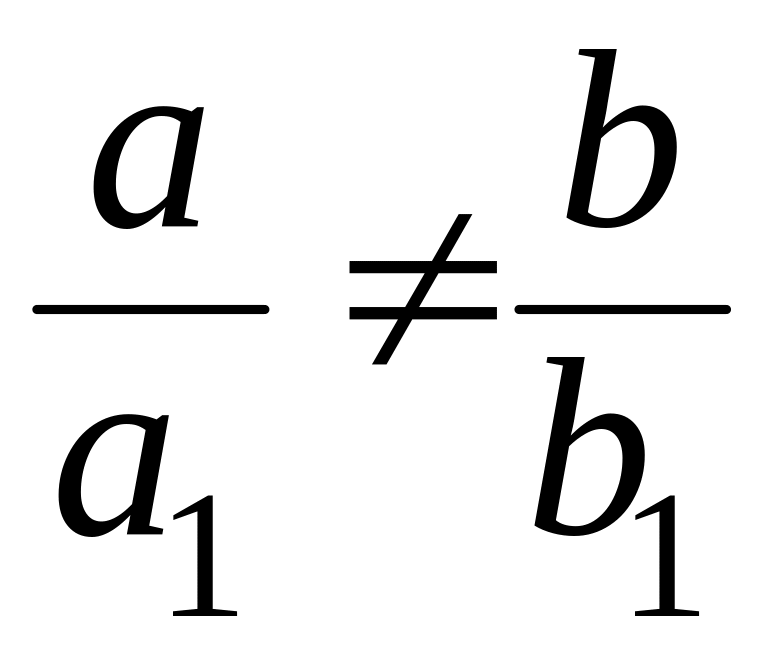
Введем новые переменные по формулам
![]()
где h и k – подбираются специальным образом. Подставляя эти переменные в (1), найдем
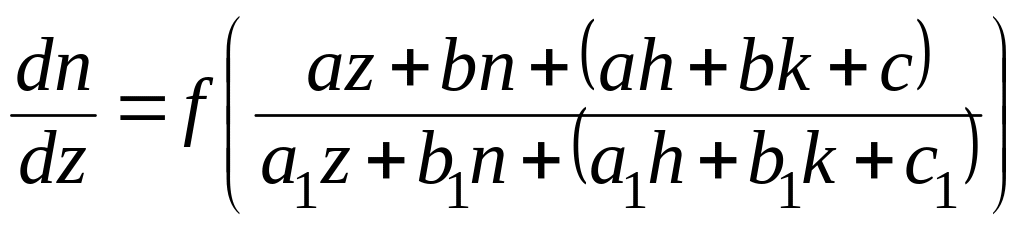 .
.
Подберем коэффициенты h и k так, что бы
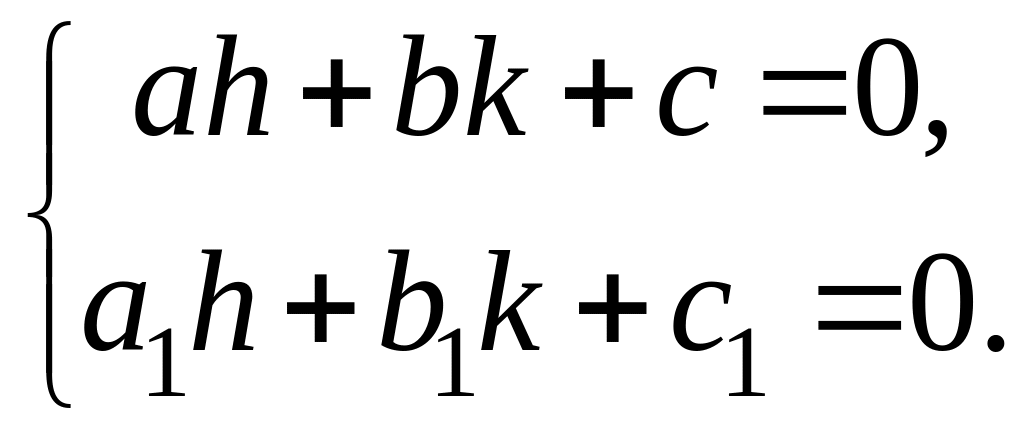
Это можно сделать,
т.к. определитель
![]()
В результате мы получим уравнение
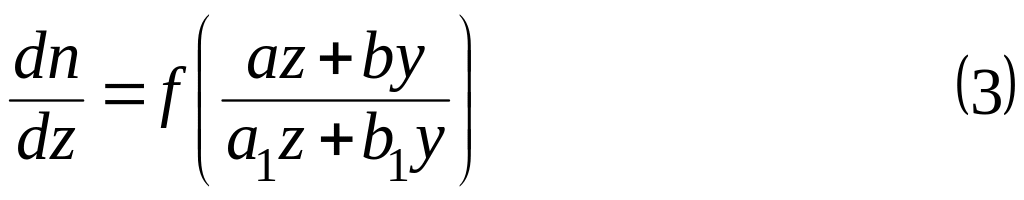
ДУ(3) есть однородное уравнение.
Пример 1.
![]() .
.
Пример 2.
![]() .
.
Решение.
![]() .
.
![]() .
.
Пусть
![]()
Тогда
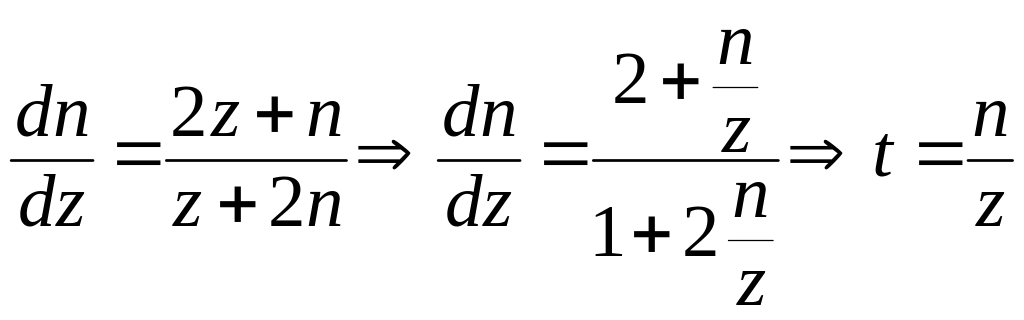 и т.д.
и т.д.
Линейные уравнения
ДУ называется линейным, если оно линейно относительно искомой функции и ее производной. Оно имеет вид
![]()
Если
![]() ,
то получаем однородное уравнение
,
то получаем однородное уравнение
![]()
соответствующее уравнению (1).
ДУ (2) есть уравнение с разделяющимися переменными. Интегрируя его, получим:
![]()
Формула (3) есть общее решение ДУ(2). Если требуется решить задачу Коши с начальным условием , то заменяя неопределенный интеграл интегралом с переменным верхним пределом, найдем
![]()
Начальное условие
![]() дает
дает
![]() .
Тогда решение задачи Коши для уравнения
(2) дает
.
Тогда решение задачи Коши для уравнения
(2) дает
![]()
Решение ЛНДУ (1) найдем методом вариации произвольной постоянной, который заключается в следующем: решение ЛНДУ ищется в том же виде, какой имеет общее решение соответствующего ЛОДУ, лишь вместо постоянной С берется функция С(x). Т.е. будем искать решение ЛНДУ(1) в виде
![]()
Подставляя (5) в (1) получим:
![]()
или
![]()
Отсюда
![]()
В результате формула (5) примет вид
![]()
Как видим, общее решение НЛДУ есть сумма общего решения соответствующего ЛОДУ и частного решения ЛНДУ.
Решение задачи Коши с начальным условием можно записать в виде

Замечание. ЛНДУ можно записать в виде
![]()
Первая часть этого уравнения имеет частную производную по y, непрерывную в области определения уравнения. По теореме Пикара линейное уравнение не имеет особых решений.
Пример 1. Решить задачу Коши:
![]()
ДУ приводящиеся к линейным
а) Уравнение Бернулли
ДУ Бернулли
![]()
легко приводится к линейному уравнению.
При
![]() ДУ(1) есть линейное уравнение. При
ДУ(1) есть линейное уравнение. При
![]() имеем ДУ с разделяющимися переменными.
Пусть
имеем ДУ с разделяющимися переменными.
Пусть
![]() .
Разделив обе части (1) на
.
Разделив обе части (1) на
![]() , где
, где
![]() ,
сделаем замену
,
сделаем замену
![]() .
Тогда
.
Тогда
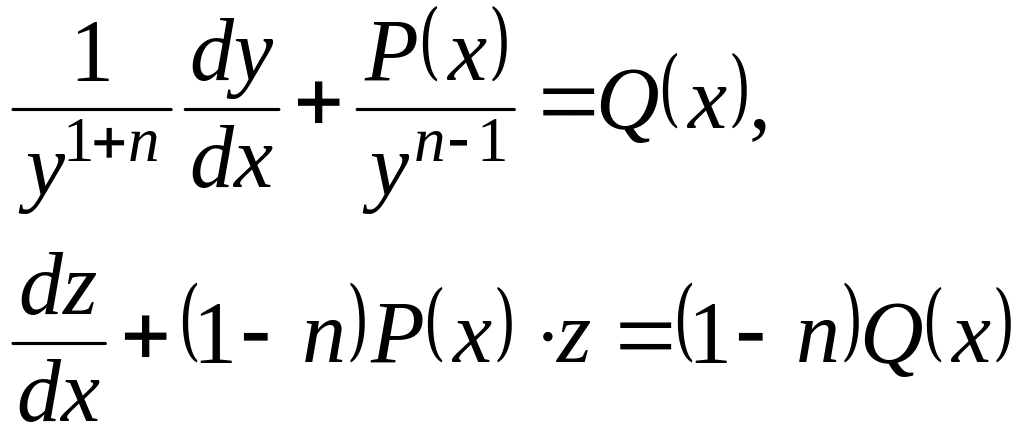
Найдя общее решение этого уравнения и вернувшись к старой функции, получим общее решение уравнения (1).
Легко убедиться, что при n>0 мы имеем еще одно решение .
Пример 1. Решить
уравнение
![]() .
.
б) Уравнение Дарбу.
ДУ вида
![]()
в котором
и
- однородные функции степени m,
и
![]() - однородная функция степени
- однородная функция степени
![]() ,
называется уравнением Дарбу.
,
называется уравнением Дарбу.
С помощью замены
![]() ,
где z
– новая неизвестная функция, уравнение
Дарбу сводится к уравнению Бернулли
относительно функции
,
где z
– новая неизвестная функция, уравнение
Дарбу сводится к уравнению Бернулли
относительно функции
![]() .
.
Пример 2.
![]()
Разделив на
![]() найдем:
найдем:
![]() .
.
Сделаем замену
![]() .
Тогда
.
Тогда
![]()
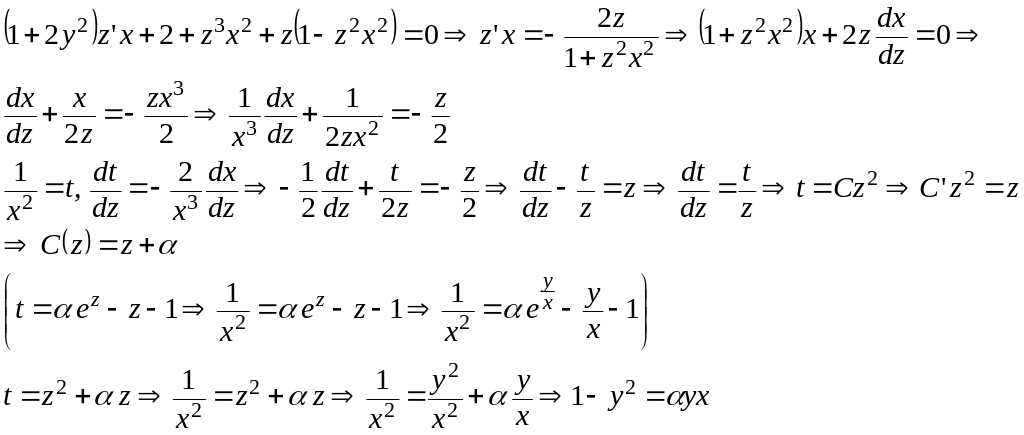 Ответ:
Ответ:
![]() - общее решение,
- общее решение,
![]() - частное решение,
- частное решение.
- частное решение,
- частное решение.
в) Уравнение Риккати.
ДУ виду
![]()
где
![]() называется уравнением Риккати т.к.
правая часть уравнения (3) удовлетворяет
теореме Пикара, то особых решений
уравнение (3) не имеет.
называется уравнением Риккати т.к.
правая часть уравнения (3) удовлетворяет
теореме Пикара, то особых решений
уравнение (3) не имеет.
ДУ (3) сводится к
ЛНДУ если только известно одно его
частное решение у,
с помощью замены
![]() ,
где z
– новая неизвестная функция.
,
где z
– новая неизвестная функция.
Действительно,
![]() .
Тогда уравнение (3) примет вид
.
Тогда уравнение (3) примет вид
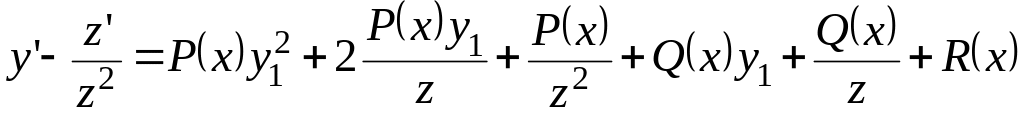
Т.к.
![]() - частное решение уравнения (3), то
- частное решение уравнения (3), то
![]()
В результате
![]() .
.
Получим линейное уравнение.
Пример 3.
![]() .
.
Решение.
![]() - частное решение. Введем новую функцию
- частное решение. Введем новую функцию
![]() ,
и т.д.
,
и т.д.
Уравнения в полных дифференциалах.
Если левая часть уравнения
![]()
представляет собой
полный дифференциал некоторой функции
![]() ,
то оно называется ДУ в полных дифференциалах.
,
то оно называется ДУ в полных дифференциалах.
В этом случае
![]()
и уравнение (1) примет вид:
![]()
Его решение дается
формулой
![]()
Возникают 2 вопроса: 1) как определить, является ли ДУ (1) уравнением в полных дифференциалах; 2) как найти функцию . Ответы на эти вопросы дает теорема 3 о приложениях формулы Грина, рассмотренная нами в разделе «И.И. функции нескольких переменных».
Теорема 3. Для того
что бы выражение
![]() было полным дифференциалом некоторой
функции
Н. и Д. что бы выполнялось условие
было полным дифференциалом некоторой
функции
Н. и Д. что бы выполнялось условие
![]() .
При этом
.
При этом
![]() ,
где криволинейный интеграл не зависит
от пути интегрирования.
,
где криволинейный интеграл не зависит
от пути интегрирования.
В качестве пути
интегрирования обычно берут ломаную
АСВ
или АС1В,
где
![]() (см. рис.1)
(см. рис.1)
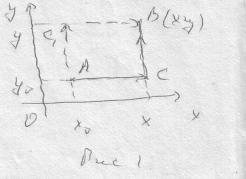
Из формулы (3) и теоремы 3 следует, что общий интеграл может быть представлен в виде
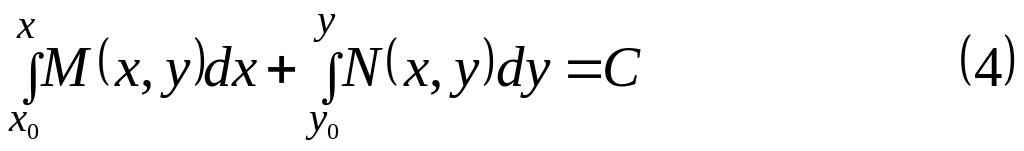
или
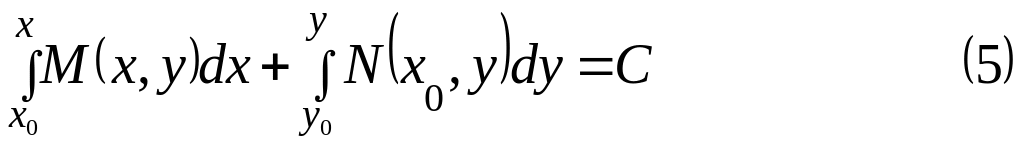
Пример 1. Решить
уравнение
![]() .
.
ДУ, приводящиеся к уравнениям в полных дифференциалах
Если левая часть уравнения
не является полным
дифференциалом, возникает вопрос, нельзя
ли найти такую функцию
![]() ,что
умножив левую часть уравнения (1) на
,
получим полный дифференциал некоторой
функции
.
Функция
называется при этом интегрирующим
множителем. Т.е. если
интегрирующий
множитель, то мы имеем
,что
умножив левую часть уравнения (1) на
,
получим полный дифференциал некоторой
функции
.
Функция
называется при этом интегрирующим
множителем. Т.е. если
интегрирующий
множитель, то мы имеем
![]()
Для всякого ли ДУ первого порядка существует интегрирующий множитель? Ответ положительный, причем число таких множителей бесконечно. Но вот найти эти интегрирующие множители часто оказывается труднее, чем решить само уравнение (1).
Покажем, как можно найти интегрирующий множитель. Из определения интегрирующего множителя имеем
![]()
или
![]()
или
![]()
Уравнение (3) есть уравнение в частных производных. Решение таких уравнений очень сложно. Но все же в некоторых случаях его удается решить.
1 случай. Множитель n зависит только от x.
Тогда
![]() и уравнение (3) примет вид
и уравнение (3) примет вид
![]()
Из формулы (4)
следует, что множитель
![]() существует тогда и только тогда, когда
дробь справа в (4) зависит только от x.
Интегрируя (4), найдем:
существует тогда и только тогда, когда
дробь справа в (4) зависит только от x.
Интегрируя (4), найдем:
![]()
![]()
2 случай. Множитель n зависит только от y.
Совершенно
аналогично показываем, что если дробь
![]() завbсит
от y,
то
завbсит
от y,
то
![]()
3 случай. Множитель
n
зависит от
![]() .
Тогда уравнение (3) примет вид
.
Тогда уравнение (3) примет вид
![]() .
.
Отсюда
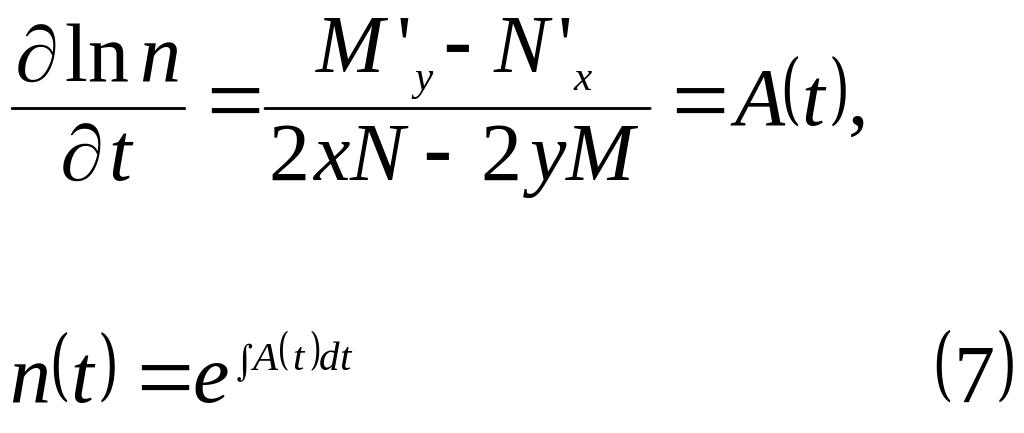
4 случай. Множитель n зависит от t=xy
Тогда уравнение (3) примет вид:
![]()
Отсюда
![]()
Где дробь
![]() зависит только от t=xy
зависит только от t=xy
Пример 1.
![]()
Решение. Будем
искать
![]() .
Из формулы (7) найдем и т.д.
.
Из формулы (7) найдем и т.д.
