Тема 3. Ду, не разделенные относительно производной. Простейшие типы ду, не разделенных относительно производной.

Рассмотрим уравнение

Если это уравнение удается решить относительно , то получаем одно или несколько уравнений

Интегрируя (2), получим решение (1). При этом возможна такая ситуация: каждое из уравнений (2) имеет единственное решение, т.е. через каждую точку области существования решения (область В) проходит одна интегральная кривая, а само уравнение (1) имеет несколько интегральных кривых, проходящих через данную точку. Как быть в этом случае с вопросом о единственности решения. Принято следующее положение. ДУ (1) имеет единственное решение задачи Коши, если через данную точку в данном направлении проходит одна и только одна интегральная кривая.

Пример 1. Решить уравнение

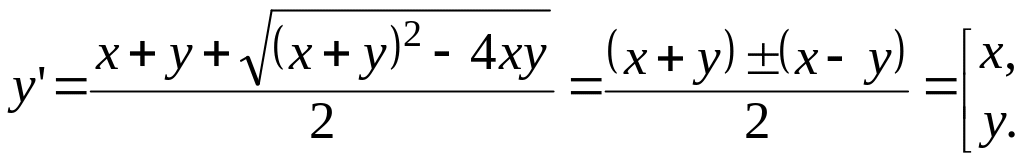
Тогда или , т.е. , или .

Решениями будут являться так же кривые, составленные из 2-х кусков: части параболы , и части гиперболы , если только в общей точке они касаются друг друга.

Для отыскания этих кусков и общей точки надо решить систему из 4-х уравнений

- ищем общую точку.

- ищем среди них точку касания.

Имеем 2 уравнения и 3 неизвестных . Пусть , тогда и .

В частности при имеем , .

Тогда решением также являются составные функци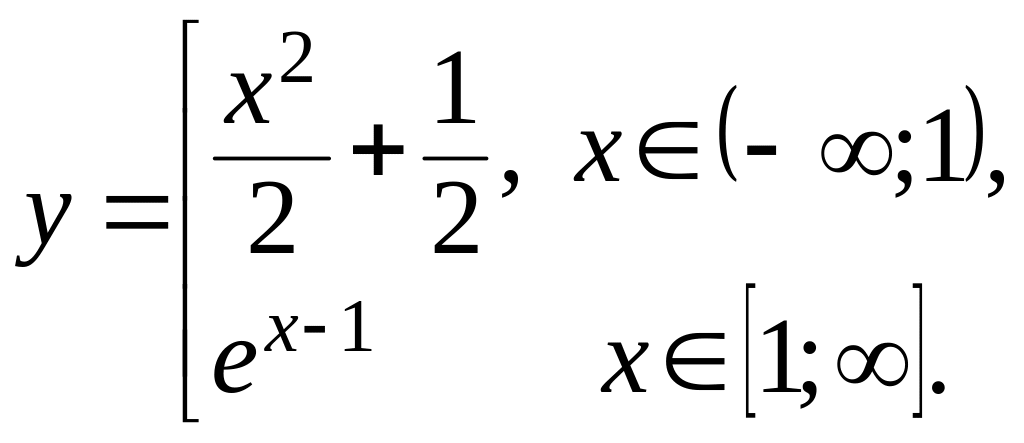и

и

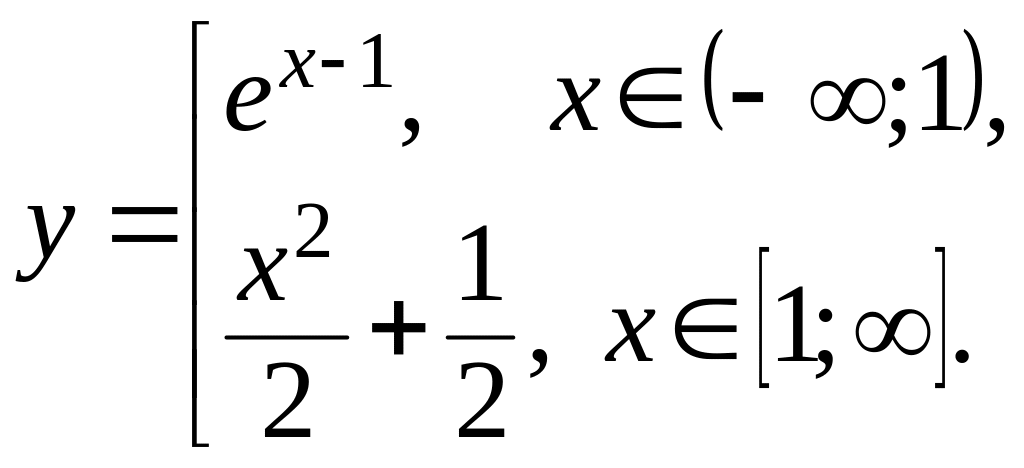
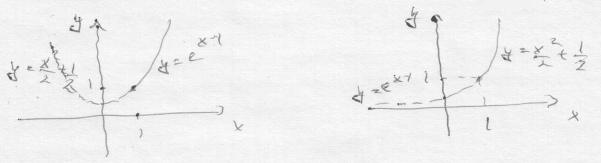
Выяснить вопрос о единственности решения. Интегральные кривые имеют направление и . Следовательно, единственность может нарушаться только на линии . Но эта линия решением не является. Поэтому данное ДУ особых решений не имеет.

ДУ (1) не всегда разрешимо относительно или ДУ (2) трудно интегрируется. Поэтому хочется найти другие способы решения. Рассмотрим частные случаи.

I.

ДУ (3) есть алгебраическое уравнение относительно . Пусть - корень этого уравнения. Тогда и . Следовательно,

- общий интеграл.

Пример 2.

- общий интеграл.

II.

Пусть (4) не разделимо ни относительно , ни . Введем параметр и заменим (4) 2мя уравнениями . Тогда из тождества найдем

Получим решение в параметрической форме

Пример 3.

Решение. Пусть . Тогда

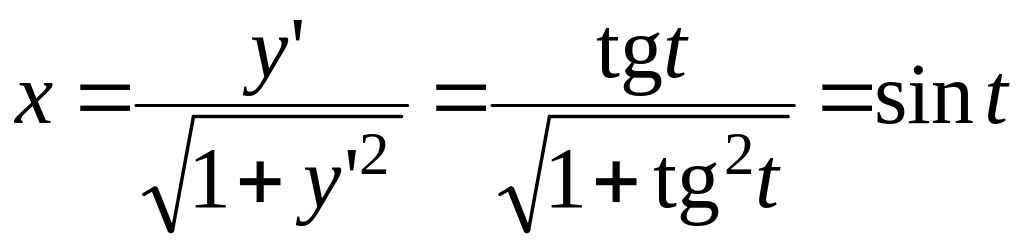
Из равенства

- общий интеграл в параметрической форме.

Можно исключить параметр : .

III.

Пусть (5) не разделимо относительно и . Тогда все делается аналогично:

.

Из

Пример 4. .

Решение. .

Из

- параметрическая форма общего решения.

Можно исключить параметр

Если уравнения (4) и (5) разрешаются относительно x и y, то удобнее применять метод дифференцирования, который мы рассмотрим ниже.

IV.

Пусть (6) не разрешается относительно . Введем параметры и по формулам

Из равенства имеем

Отсюда

Метод дифференцирования

Пусть уравнение

Разрешимо относительно или или , т.е.

или

Пусть . Уравнения

и

продифференцируем по и соответственно

или

ДУ и есть ДУ относительно . Решив их найдем общие интегралы

или

Тогда решения уравнений (2) или (3) будут в параметрической форме иметь вид

или .

Пример 1.

Решение. - параметрическое задание переменной . Продифференцировав его по получим:

или

Т.е.

или

Исключим параметр р

- частное или особое решение ИЛИ

- общее решение

Уравнения Логранжа и Клеро

ДУ вида

т.е. линейное относительно и , называется ДУ Лагранжа. При ДУ (1) принято называть Клеро:

Рассмотрим уравнение Лагранжа, т.е. . Пусть . Продифференцировав уравнение

по х найдем

или где

а) Из (3) следует , если

ДУ (4) есть линейное уравнение относительно х. Решив его, найдем решение уравнения (1) в параметрическом виде

Система (5) дает общий интеграл

б) Если , то (3) примет вид

Получим систему . Если эта система имеет решение , то кроме общего решения (5) ДУ (1) имеет решение - частное или особое.

Рассмотрим уравнение Клеро. Аналогичным образом получим уравнение (3) в виде

Отсюда или

Тогда уравнение Клеро имеет общее решение

или - частное или …

Пример 1. - уравнение Логранжа

Решение. Имеем , где отсюда

а)

Тогда - частное или особое решение.

б)

решим это неоднородное линейное уравнение.

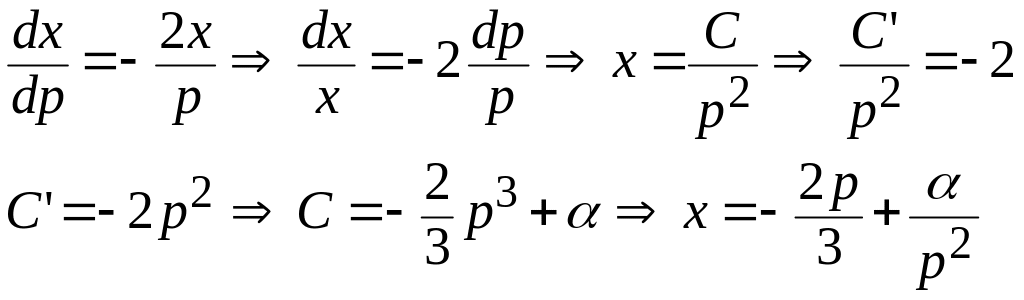
Т.е. 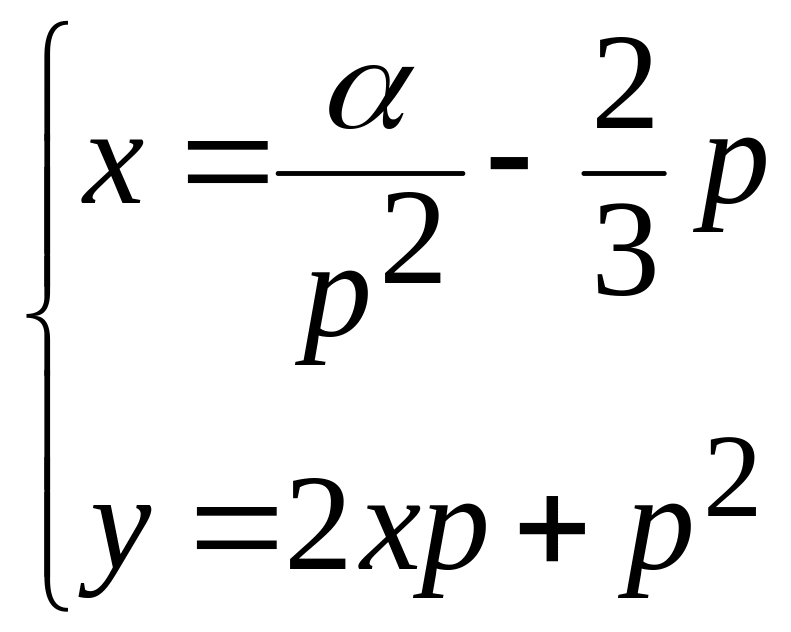- параметрическая форма общего решения

Пример 2. - уравнение Клеро

Решение.

После дифференцирования получим

или

или

- общее решение

- частное или особое решение

Условие Липшица

Определение 1. Функция называется непрерывной на , если для любых и из выполняется условие .

Определение 1’. Функция называется непрерывной на , если существует число L>0 такое что

, где Е>0 – любое.

Определение 2. Функция удовлетворяет условию Липшица на , если существует число b>0 такое, что для любых и из выполняется неравенство .

Пример 1. удовлетворяет условию Липшица на любом отрезке . Действительно .

Пример 2. Если функция дифференцируема на , то она удовлетворяет условию Липшица. Действительно из формулы Лагранжа следует:

.

Если функция удовлетворяет условию Липшица на отрезке , то она не обязательно дифференцируема на отрезке .

Пример 3. Функция не дифференцируема на отрезке , но удовлетворяет условию Липшица

.

Определение 3. Функция удовлетворяет условию Гельдера с показателем . Если существует число L>0, такое что

Пример 4. удовлетворяет условию Гельдера с показателем на любом отрезке, содержащем 0 С если отрезок не содержит точку х=0, то функция дифференцируема . Действительно

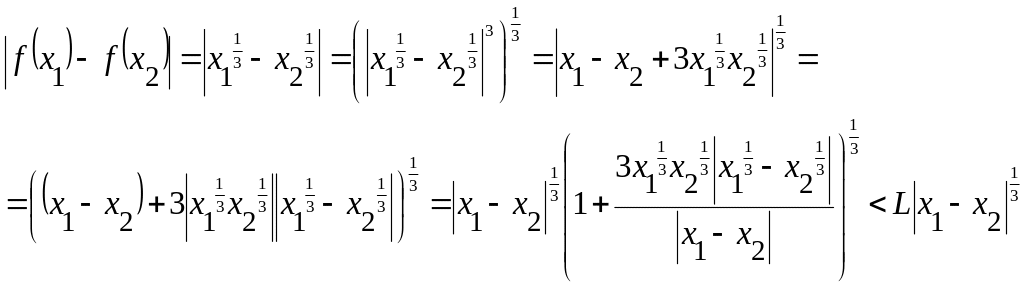
где

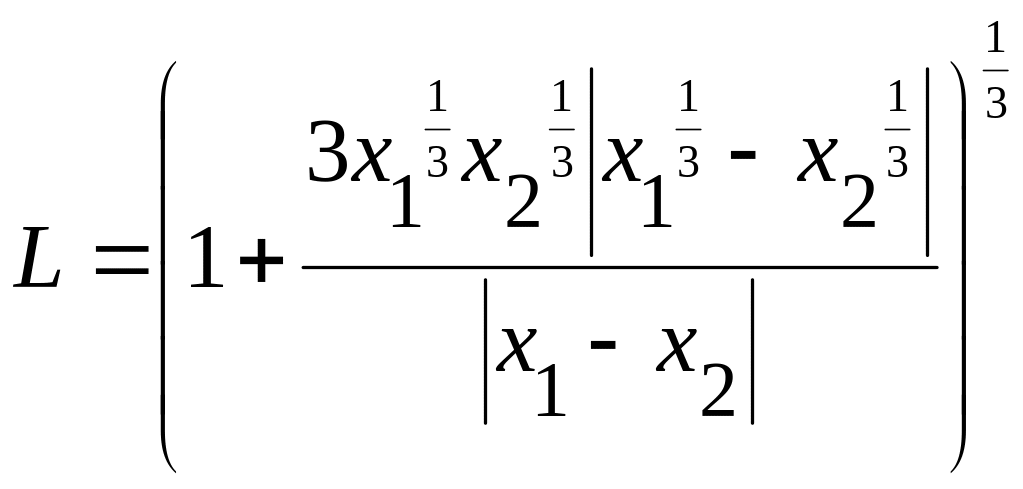
Функция класса Гельдера входят в класс непрерывных функций и содержит в себе класс функций …

Теоремы о существовании и единственности решения задачи Коши.

Особые решения.

1. Случай уравнения .

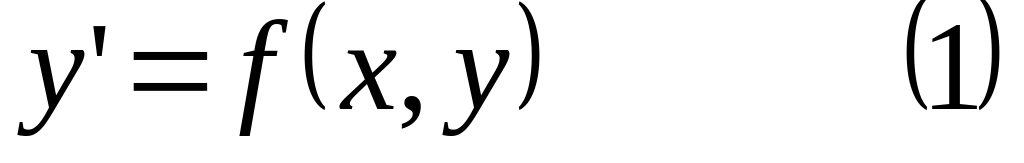Теорема 1. Если непрерывна в области и удовлетворяет в этой области условию Липшица относительно у:

то существует единственное решение , удовлетворяющее начальному условию .

Определение 1. Решение уравнения (1) называется особым, если в каждой точке этого решения нарушается условие единственности решения.

С геометрической точки зрения, интегральная кривая является особой, если через каждую ее точку проходят более одной интегральных кривых.

Особые решения, в силу теории Пикара, могут быть только в тех точках, где не существует или равна . Например, уравнение вида , где многочлен относительно у не может иметь особых решений (линейное уравнение, уравнение Риккати, уравнение Бернулли с показателем n>0). Так же особых решений не имеет и уравнение , где и многочлены относительно у. Действительно, если в точке , то надо рассмотреть неявное и явное уравнения , которое не имеет особых решений.

Для того что бы найти особые решения уравнения (1) надо найти точки, в которых не существует или равна . Затем проверить, удовлетворяет ли это множество точек уравнению и, если удовлетворяет, проверить свойство единственности.

Пример 1. . Найти особые решения.

Решение. Имеем .

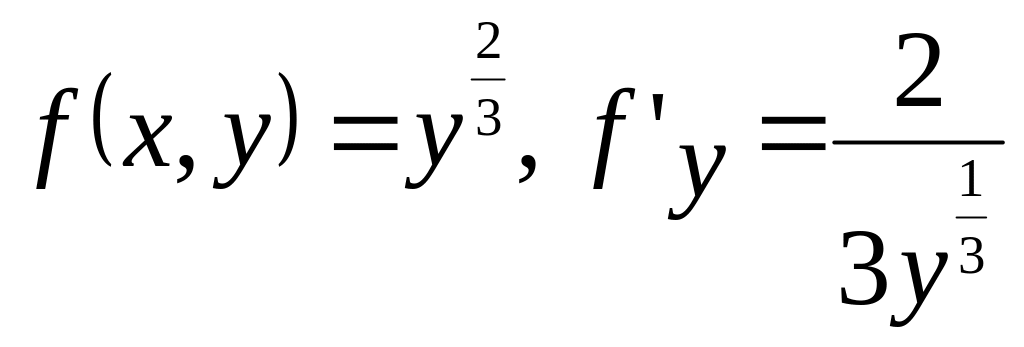Особым решением может быть линия .

Эта линия удовлетворяет уравнению.

Найдем общее решение .

Свойство единственности можно проверить 2мя способами.

1 способ. (Геометрический)

Через каждую точку прямой проходят 2 решения: и одна кривая из семейства .

2 способ (алгебраический).

Система уравнений

имеет бесконечное множество решений . Итак, - особое решение.

Пример 2. . Найти особые решения.

Решение. Имеем 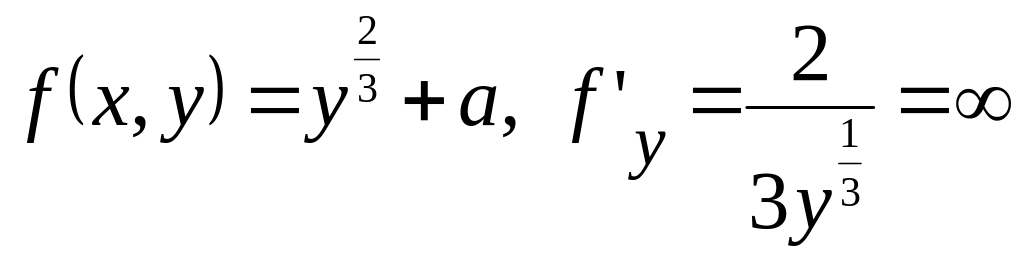при . Но прямая не удовлетворяет уравнению. Поэтому это уравнение особых решений не имеет.

2. Случай уравнения

В случае (4) единственность решения понимается так: уравнение (4) имеет единственное решение удовлетворяющее начальному условию (3) если через точку в направлении проходит единственная интегральная кривая.

Теорема 2. Если функция в замкнутой окрестности точки удовлетворяет условиям

1) непрерывна по всем аргументам;

2) существует, причем ;

3) существует , причем , то существует единственное решение уравнения (4), удовлетворяющее начальному условию (3) и проходящее в направлении .

Теорема Пикара является частным случаем этой теоремы.

Рассмотрим случай, когда нарушается условие (2) теоремы 2. Тогда должна иметь место система уравнений.

где . Исключая параметр p, найдем уравнение, которое называется p-дискриминантной кривой. Только среди p-дискриминантных кривых могут быть особое кривые.

Т.е. для отыскания особых интегральных кривых надо:

1) найти p-дискриминантные кривые;

2) проверить являются ли они решениями;

3), если являются проверить, удовлетворяют ли они условию единственности решения.

Пример 3. Найти особые решения уравнения .

Решение. 1)

- p-дискриминантные кривые.

2) - решения;

3) Найдем общий интеграл:

Через каждую точку прямых проходит 2 решения: сама прямая и синусоида. Следовательно, - особые решения.

Пример 4. Найти особые решения уравнения

.

Решение. 1)

- р-дискриминантные кривые;

2) удовлетворяют уравнению;

3) Найдем общий интеграл:

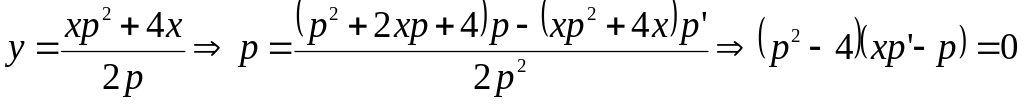
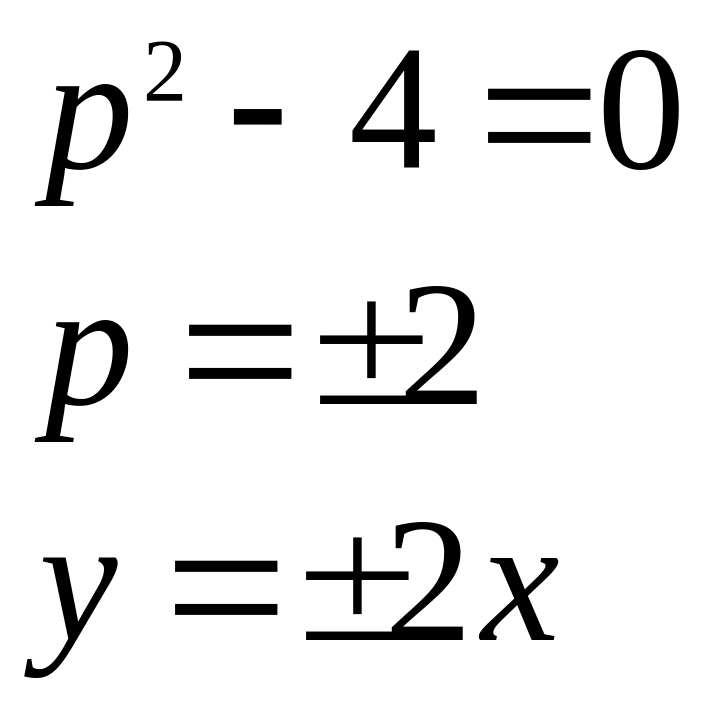или 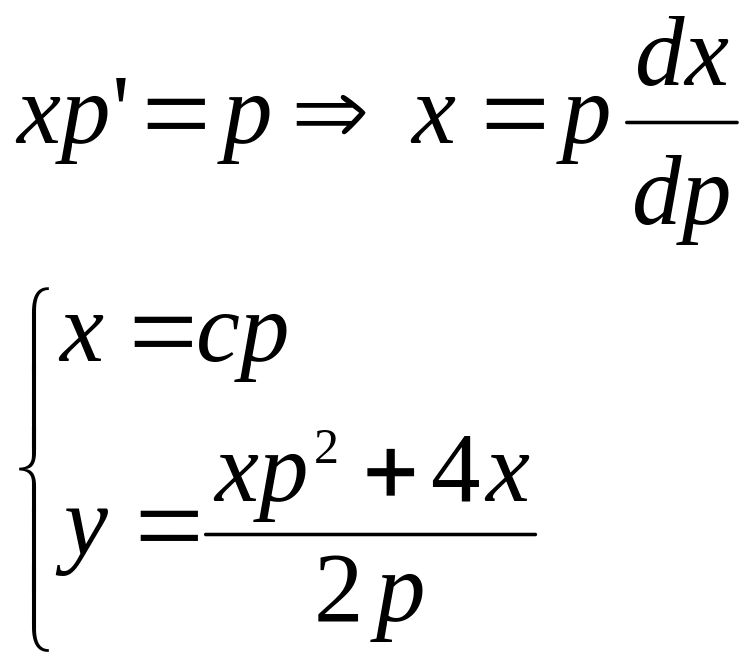- параметрическая форма

- общий интеграл.

Свойство единственности проверим алгебраическим способом. Из системы следует:

,

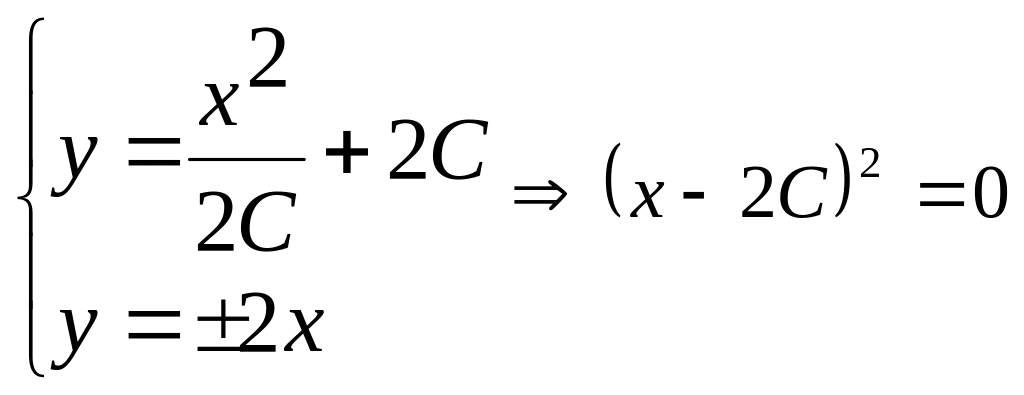т.е. решением является множество точек . Т.е. - особое решение.

Во всех рассмотренных примерах особая интегральная кривая в каждой своей точке касается какой-либо кривой из семейства интегральных кривых. Кривые, обладающие таким свойством, называют огибающими. Из курса аналитической геометрии известно, что огибающие кривые удовлетворяют системе

где - общий интеграл уравнения (4). Исключив из системы (6) параметр С, найдем С-дискриминантные кривые. Именно среди них могут быть особые интегральные кривые.

Отыскание особых интегральных кривых с помощью С-дискримининтных кривых более предпочтительно.

Пример 5. Найти особые решения методом С-дискриминантных кривых уравнения .

Решение. 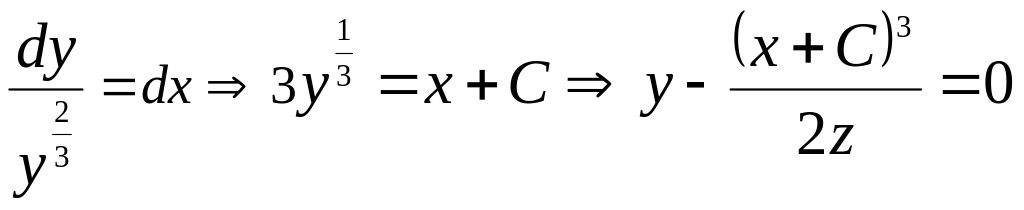- общий интеграл.

Т.е. .

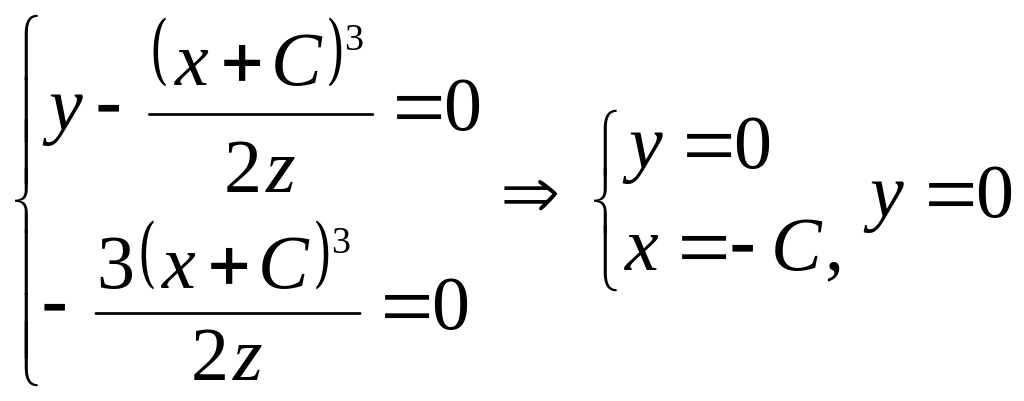- С-дискриминантная кривая.

Легко проверить (см. пример 1), что - особое решение.