30

Раздел VIII. Обыкновенные дифференциальные уравнения. (оду).

Литература.

1.Степанов В.В. «Курс ДУ».

2.Понтрячик Л.С. «ОДУ».

3.Матвеев Н.М. ДУ.

4.Петровский И.Г. «Лекции по теории ОДУ».

5.Эльсгальц Л.Э. «ДУ».

6.Смирков В.И. «Курс высшей математики. Т2».

7.Свешников А.Г., Тихонов Н.А., Васильева А.Б. «ДУ».

8.Филипов А.В. «Сборник задач по ДУ».

9.Берман Г.Н. «Сборник задач и упражнений по математическому анализу».

Введение. Основные понятия теории ДУ.

I. ДУ называется уравнение, содержащее независимые переменные, искомую функцию и ее производные. Порядок старшей производной, входящей в уравнение, называется порядком уравнения. Если независимая переменная одна, то уравнение называется ОДУ. В противном случае оно называется уравнением в частных производных.

ДУ имеют многочисленные и самые разнообразные применения в механике, физике, астрономии, дифференциальной геометрии и т.д. и т.п.

Пример 1. Простейшей задачей теории ДУ является задача отыскания первообразной функции , - известная функция, - неизвестная.

Пример 2. Уравнение где характеризует скорость распада, описывает процесс радиоактивного распада вещества. Проверкой можно убедиться, что его решением является функция , где - масса исходного вещества, - начальный момент времени. - период полураспада вещества, т.е. когда . Тогда . Отсюда . Коэффициент , а затем и Т находят экспериментальным путем.

Пример 3. Процесс колебания пружины, маятника в полярных координатах, описывается уравнением .

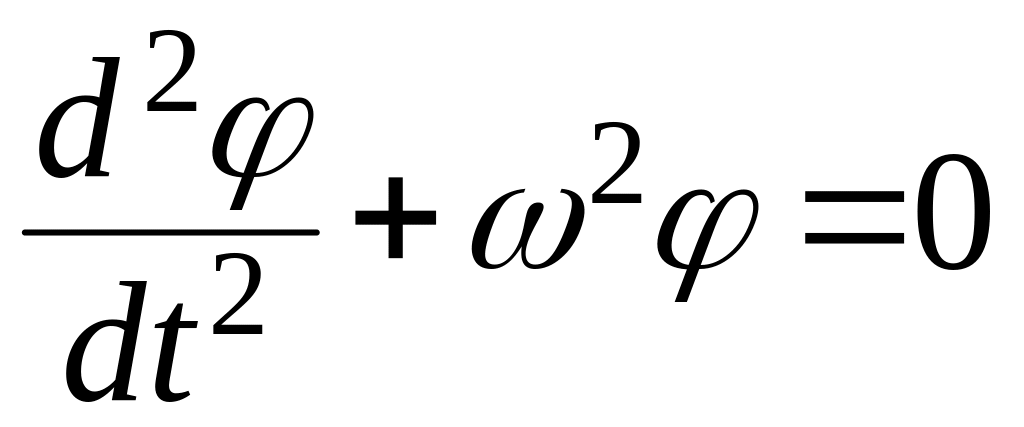Проверкой можно убедиться, что решением является функция , где - произвольные постоянные.

Пример 4. Уравнение описывает процесс колебания струны.

В первых трех примерах рассмотрены ОДУ, в последнем примере – уравнение в частных производных.

В дальнейшем мы будем рассматривать лишь ОДУ.

II. В общем случае ОДУ n-го порядка записывается в виде .

Но главным образом рассматриваются ОДУ разделенные относительно старшей производной

Наиболее хорошо изучены линейные ОДУ, т.е. уравнения линейные относительно искомой функции и ее производных

.

Решением ОДУ n-го порядка называется функция, имеющая непрерывные производные n-го порядка включительно и образующая это уравнение в тождество. Кривая, соответствующая решению ОДУ, называется интегральной кривой. Процесс отыскания решения ОДУ называется интегрированием уравнения.

Пример 5. Уравнение имеет семейство решений , где С – произвольная постоянная.

Пример 6. Решением уравнения является функция , где С₁ и С₂ – различные производные постоянные.

Пример 7. Решением уравнения имеет вид , где С₁, С₂, . . . С_n – различные произвольные постоянные.

Как видно из приведенных примеров, решение ОДУ n-го порядка представляет собой целое семейство решений (или интегральных кривых), зависящее от n различных произвольных переменных.

Определение 1. Общим решением ОДУ n-го порядка называется решение, зависящее от n-произвольных постоянных.

Определение 2. Решение, получающееся из общего решения при фиксированных значениях С₁, С₂, . . . С_n называется частным решением.

Заметим однако, что не всякое частное решение получается из общего решения.