11.2 Удар

К

Рисунок 11.2

динамическому виду нагрузки относится так же ударная нагрузка. С явлением удара приходиться иметь дело, когда скорость рассматриваемого элемента конструкции или соприкасающихся с ним частей в очень короткий промежуток времени изменяется на конечную величину. Определение силы удара весьма затруднительно, так как неизвестно время соударения, поэтому в инженерной практике обычно пользуются энергетическим методом. В качестве примера рассмотрим систему с одной степенью свободы (рис. 11.2,а), которая представляет собой пружину с коэффициентом жесткости с и падающий на нее груз массой m с высоты H.

Груз m при касании пружины будет обладать кинетической энергией Т, которую можно выразить через скорость V_к груза в момент касания или высоту H: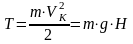 . (11.7)

После того, как груз коснется пружины, он начет деформировать пружину. Когда вся кинетическая энергия груза перейдет в потенциальную энергию сжатой пружины, груз остановится (рис. 11.2, б), пружина получит свою наибольшую динамическую деформацию _Д, а сила, сжимающая пружину, достигнет максимума. При составлении энергетического баланса здесь нужно учитывать изменение потенциальной энергии П груза на динамической деформации _Д: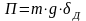 . (11.8)

Упругая энергия U сжатой пружины: . (11.9)

Составим энергетический баланс: ,или ,который перепишем в следующем виде: .

Рассматривая статическое равновесие упругой системы (рис. 11.2, в), отношение силы тяжести груза к жесткости пружины равно статической деформации пружины _ст: .

Получили квадратное уравнение, из которого динамическая деформация определится как: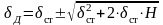 . (11.11)

Поскольку знак минус в этом выражении не соответствует физической стороне рассматриваемой задачи, следует сохранить знак плюс. Запишем выражение (11.11) в виде: . Величину, стоящую в скобках называют коэффициентом динамичности: . Коэффициент динамичности, выраженный через скорость груза в момент касания пружины с учетом выражения (11.7) будет равен: .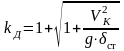

Окончательно динамическая деформация пружины определится как: . Динамический коэффициент показывает, во сколько раз деформация при ударе больше деформации при статическом приложении нагрузки. В том же отношении изменяются внутренние силы и напряжения: .

Из анализа выражения 11.14 видно, что коэффициент динамичности зависит от кинетической энергии падающего груза. В случае если груз опускается на упругую систему мгновенно без начальной скорости, динамическая деформация уже вдвое превышает статическую. Соответственно в два раза большими оказываются и напряжения.

Коэффициент динамичности, а, следовательно, и динамические напряжения, также зависят от жестокости упругой системы. При большей жесткости статические деформации имеют меньшие значения, а динамические напряжения при этом увеличиваются. Поэтому снижение напряжений при ударе может быть достигнуто уменьшением жесткости системы.

Зависимости для определения динамических напряжений и деформаций, полученные на примере падения груза на пружину применимы и для других упругих систем (расчет на удар при растяжении – сжатии, кручении и изгибе).В каждом случае придерживаются следующего порядка расчета:

а) в месте падения груза к упругой системе прикладывают статическую нагрузку, равную весу падающего груза;

б) определяют статическую деформацию упругой системы;

в) определяют напряжения в материале, возникающие от приложения статической нагрузки;

г) определяют коэффициент динамичности;

д) определяют динамические напряжения и деформации.

е) сравнивают напряжения при ударе с допускаемыми напряжениями: . (11.17)

Обычно коэффициент запаса n_т принимают равным n_т = 2.

Полученные выше выражения получены без учета массы упругой системы, к которой прикладывается ударная нагрузка. Учет массы дает меньшие значения динамических напряжений, поэтому, рассчитывая конструкции без учета ее массы, мы получаем дополнительный запас прочности.