Билет26

Те́нзор напряже́ний — тензор второго ранга, состоящий из девяти величин, представляющих механические напряжения в произвольной точке нагруженного тела. Эти девять величин записываются в виде таблицы, в которой по главной диагонали стоят нормальные напряжения в трёх взаимно перпендикулярных осях, а в остальных позициях — касательные напряжения, действующие на трёх взаимно перпендикулярных плоскостях.

Нормальное напряжение  считается положительным, если оно направлено от площадки. Касательное напряжение  считается положительными, если изображающий его вектор стремится вращать параллелепипед по часовой стрелки относительно любой точке, лежащей внутри параллелепипеда. Отрицательными считаются напряжения обратных направлений.

Закон парности касательных напряжений – касательные напряжения на двух любых, но взаимно перпендикулярных площадках, направленные перпендикулярно к линии пересечения площадок, равны по величине. При этом они стремятся повернуть элемент в разные стороны.

При изменении ориентации граней выделенного элемента меняются также действующие на его гранях напряжения. Можно провести такие площадки, на которых касательные напряжения равны нулю  главные площадки, а нормальные напряжения на этих площадках называют главными напряжениями.

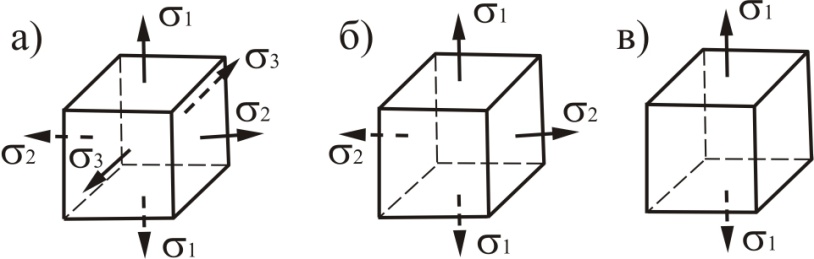
Виды: Если отличны от нуля все три главных напряжения, то напряженное состояние называется трехосным или объемным (рис. 4.2, а).

Е

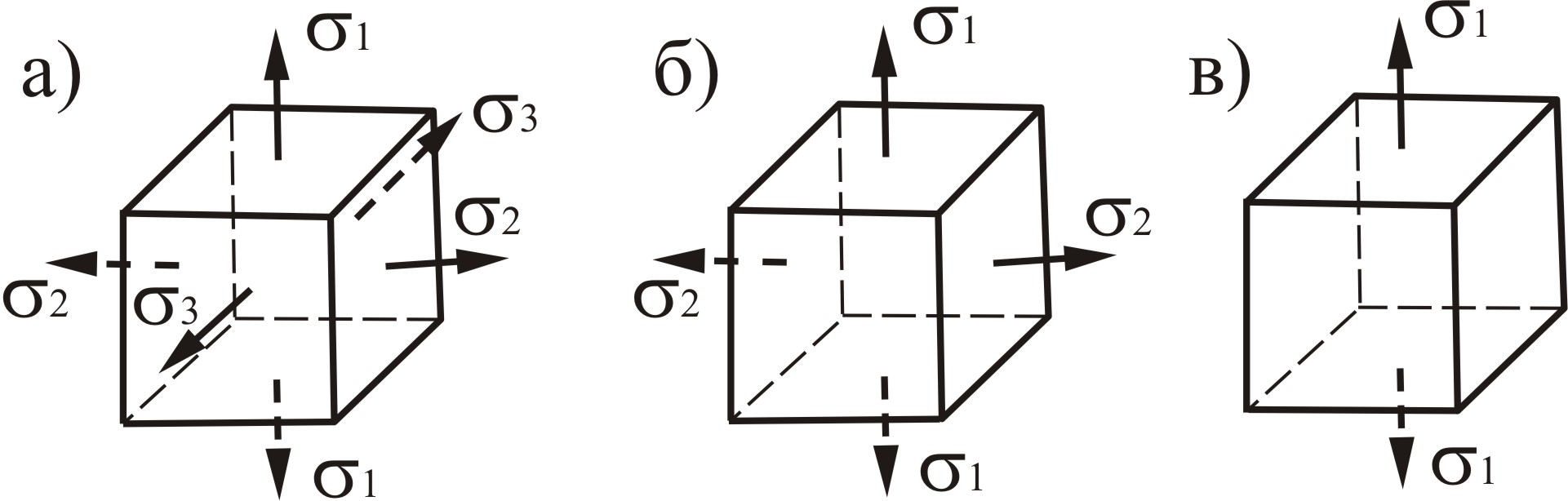
Рисунок 4.1

сли равно нулю одно из главных напряжения, то напряженное состояние называется двухосным или плоским (рис. 4.2, б).

Если равно нулю два главных напряжения, то напряженное состояние называется одноосным или линейным

Билеет27

Линейным или одноосным называется напряженное состояние, при котором два из трех главных напряжений равны нулю (рис в)

Плоским или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю (рис б)

Объемным или трехосным называется напряженное состояние, при котором все три главных напряжения отличны от нуля (рис. 4.2,а). Для объемного напряженного состояния справедливо равенство:

.

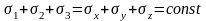Обобщенный закон Гука

Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного напряженного состояния. Он может быть получен на основании закона Гука для линейного напряженного состояния и принципа независимости действия сил. Представляя объемное напряженное состояние в виде суммы трех линейных напряженных состояний, и учитывая, что при линейном напряженном состоянии и 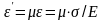, выражения для деформации в направлении действия главных напряжений будут иметь вид:

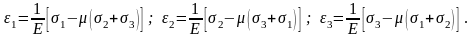
Эти выражения носят название обобщенного закона Гука, записанного для главных площадок. Деформации e₁, e₂ и e₃, в направлении главных напряжений называются главными деформациями.

Билет28

Первая гипотеза прочности: гипотеза наибольших нормальных

напряжений

Согласно этой теории, преимущественное влияние на прочность оказывает величина наибольшего нормального напряжения.

Критерий наибольших нормальных напряжений из трех главных напряжений учитывает только одно – наибольшее, полагая, что два других не влияют на прочность.

Условие нарушения прочности:

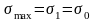, (5.1)

где ₁  наибольшее из главных напряжений для исследуемого напряженного состояния; ₀  предельное напряжение, полученное из опыта на одноосное растяжение.

Условие прочности:

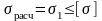, (5.2)

где 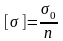– допускаемое напряжение; n  коэффициент запаса прочности (n > 1).

Данная теория дает удовлетворительные результаты лишь для очень хрупких материалов (камень, керамика, инструментальные стали и т.п.).

5.2 Вторая гипотеза прочности: гипотеза наибольших удлинений

Причиной наступления предельного напряженного состояния в материале являются наибольшие относительные удлинения.

Общее условие разрушения для объемного напряженного состояния, когда главные деформации :

,

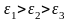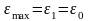где ₁  расчетная величина наибольшего удлинения для исследуемого напряженного состояния; ₀  предельное опытное значение относительного удлинения, при одноосном растяжении.

Как известно, из обобщенного закона Гука можно записать:

;

Используя закон Гука при одноосном растяжении-сжатии, запишем:

.

Тогда условие разрушения записывается в виде:

.

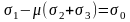Левую часть формулы назовем расчетным напряжением .

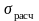Условие прочности:

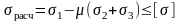. (5.3)

5.3 Третья гипотеза прочности: гипотеза наибольших касательных

напряжений

Причиной наступления предельного напряженного состояния являются наибольшие касательные напряжения.

Общее условие разрушения:

,

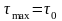где _max  расчетная величина наибольшего касательного напряжения для исследуемого напряженного состояния; ₀  предельное опытное значение касательного напряжения, определяемое из опыта на одноосное растяжении.

Как известно, в случае объемного напряженного состояния наибольшее касательное напряжение:

,

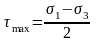а в случае одноосного растяжения-сжатия:

.

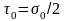Тогда условие разрушения запишется в виде:

.

Условие прочности

.

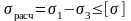Для плоского напряженного состояния:

.

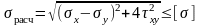Для упрощенного плоского напряженного состояния ( ):

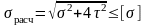. (5.4)

5.4 Четвертая гипотеза прочности: гипотеза потенциальной энергии

формоизменения

Причиной наступления предельного напряженного состояния материала является достижение удельной потенциальной энергией формоизменения своей критической величины.

Гипотеза основывается на предположении о том, что количество удельной потенциальной энергии деформации, накопленной к моменту наступления предельного напряженного состояния в материале, одинаково как при любом сложном напряженном состоянии, так и при простом растяжении.

Гипотеза связывается с развитием только пластических деформаций, характеризующихся изменением формы тела без изменения объёма.

Полная удельная потенциальная энергия состоит из двух частей:

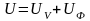, (5.5)

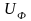
где  энергия, вызывающая только изменения объема;  энергия, вызывающая только изменения формы кубика с ребром равным единице.

Условие отсутствия пластических деформаций:

,

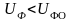где U_Ф  расчетная величина энергии формоизменения для исследуемого напряженного состояния; U_ФО  предельное опытное значение той же энергии при одноосном растяжении.

В общем случае напряженного состояния энергия формоизменения определяется по формуле:

.

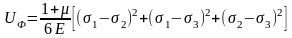В случае предельного состояния текучести при простом растяжении:

,

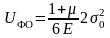где ₀ – предельное опытное значение напряжения при одноосном растяжении.

Условие прочности:

,

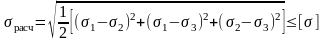где [] – допускаемое напряжение при растяжении.

В частном случае плоского напряженного состояния при _у = 0, _х = , _ху =  условие прочности записывается в виде:

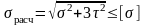. (5.7)

Билет29

Сдвигом - называется такой вид нагружения бруса, при котором в его поперечных сечениях из шести составляющих главного вектора и главного момента внутренних сил, от нуля отличается только поперечная сила.

Внутренняя поперечная сила Q в поперечном сечении бруса на участке действия сосредоточенных мало, то можно пренебречь величиной изгибающего момента. При этом распределение касательных напряжений по сечению неравномерно, так как внешняя поверхность бруса свободна от осевой нагрузки и по закону парности касательных напряжений, в верхних и нижних точках сечения касательные напряжения равны нулю.

Таким образом, касательное напряжение при сдвиге (срезе) определяется уравнением:

,

Деформация бруса при сдвиге в зоне действия усилия, предшествующая разрушению от среза, заключается в перекашивании прямых углов элемента (рис. 5.4).

Аналогично растяжению (сжатию) закон Гука при сдвиге в абсолютных координатах имеет вид:

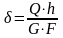
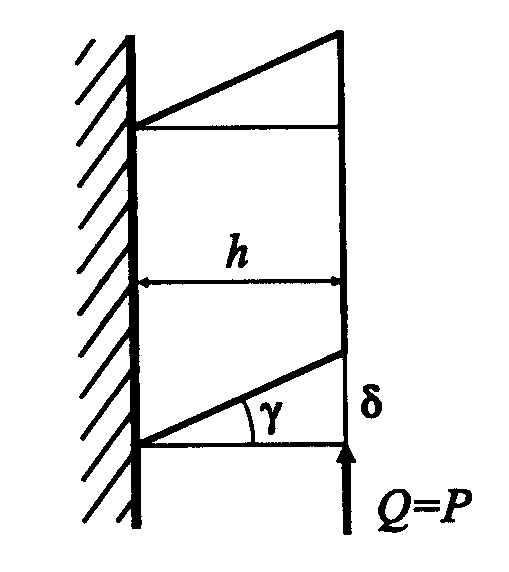
Рисунок 5.4  Деформация бруса

при сдвиге:   абсолютный сдвиг;

tg =    / h  относительный

сдвиг или угол сдвига

. (5.9)

где G  модуль сдвига или модуль упругости второго рода.

Если по граням элемента действуют только касательные напряжения (рис. 5.5), то такой вид напряженного состояния называется чистым сдвигом.

Билет30

закон Гука при сдвиге в абсолютных координатах имеет вид:

Рисунок 5.4  Деформация бруса

при сдвиге:   абсолютный сдвиг;

tg =    / h  относительный

сдвиг или угол сдвига

. (5.9)

где G  модуль сдвига или модуль упругости второго рода.

Модуль сдвига связан с модулем упругости первого рода и коэффициентом Пуассона следующим, что подтверждают опыты, уравнением:

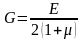. (5.10)

Для стали модуль сдвига примерно равен 810⁴ МПа. Из уравнения (5.9) с учетом (5.8) может быть получен закон Гука при сдвиге в относительных координатах:

, или .

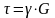билет31

Расчет на прочность

при сдвиге

Условие прочности при сдвиге имеет вид:

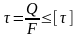, (5.13)

где []  допускаемое касательное напряжение, которое в первом приближении принимается равным [] = (0,5…0,6)[].

Расчет заклепочного соединения

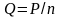, где Р  сила, действующая на соединение; п  число заклепок.

Условие прочности заклепок на срез: ,где F =  d ²/4  площадь поперечного сечения заклепки диаметром d; [] = (0,60,8)[]  допускаемое касательное напряжение.

Условие прочности на смятие имеет вид:

Расчет болтового соединения

Таким образом, условие прочности болта на срез принимает вид:

.

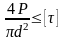Условие прочности на смятие имеет вид:

.

Билет32

Д еформация кручения вызывается парами сил, плоскости действия которых перпендикулярны к оси стержня. Поэтому при кручении в произвольном поперечном сечении стержня из шести внутренних силовых факторов возникает только один – крутящий момент M_к (рис. 6.1). Как показывают опыты, поперечные сечения при кручении поворачиваются одно относительно другого вокруг оси стержня, при этом длина не меняется.

Стержни, работающие на кручение, обычно называют валами.

Определение крутящего момента и построение эпюр крутящих моментов

Для определения напряжений и деформаций произвольного вала необходимо знать величину крутящих моментов на его отдельных участках.

Крутящий момент М_кр в произвольном сечении вала равен сумме внешних моментов М_к, расположенных по одну сторону сечения.

Крутящий момент М_кр считается положительным, если при наблюдении с торца вдоль оси рассматриваемой части он стремится вращать сечение по часовой стрелке (рис. 6.9).

Рассмотрим в качестве примера построение эпюры крутящих моментов для трансмиссионного вала (рис. 6.10).

Разбиваем вал на участки , , .

Проведя произвольное сечение на первом участке:

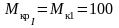, Н·м.

Для второго участка:

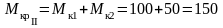, Н·м.

На третьем участке рассматриваем правую часть от сечения, в котором определяем М_кр:

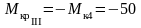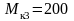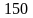, Н·м. Построенная эпюра показывает, что хотя к валу и приложен момент Н·м, наибольший крутящий момент в сечении равен лишь Н·м. Эту величину и следует использовать при расчете на прочность и жесткость.