Пределы применимости формулы Эйлера

Получив значение критической силы, мы можем найти и значение критического напряжения _кр, разделив критическую силу Р_кр на площадь сечения: .

Учитывая, что отношение 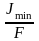равно квадрату минимального радиуса инерции поперечного сечения , получим: , где   безразмерный коэффициент называемый гибкостью стержня: 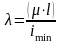, (10.6)

П

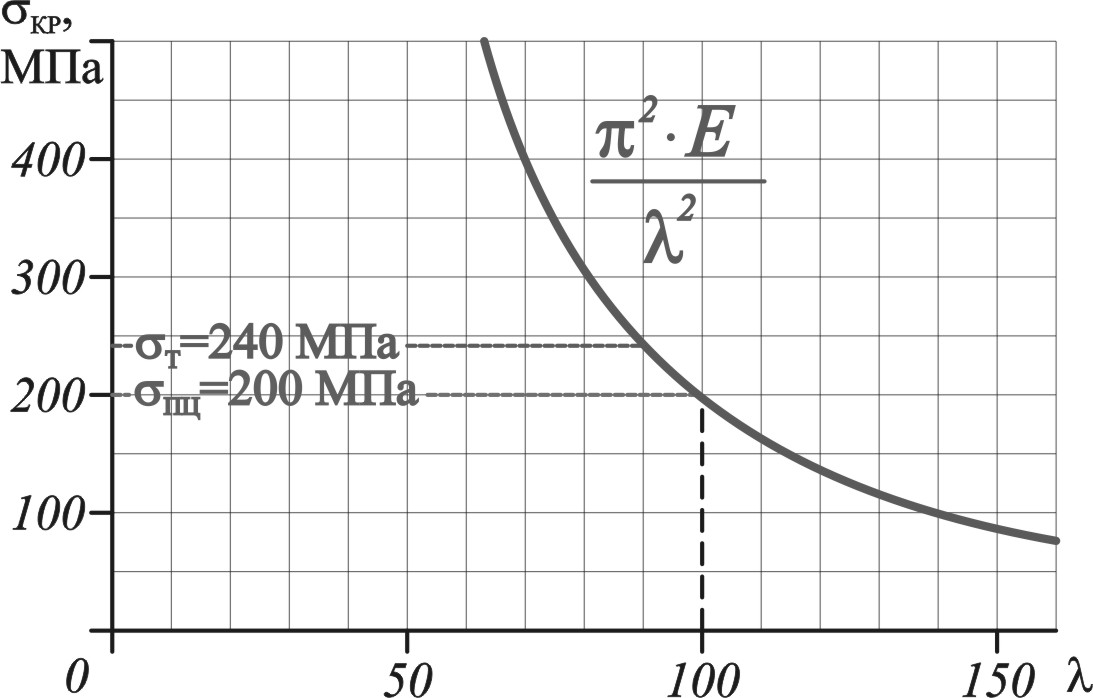
Рисунок 10.8. Гипербола Эйлера

олученная зависимость (10.5) представляет собой гиперболическую кривую, называемую гиперболой Эйлера.

В качестве примера на рисунке 10.8 приведена гипербола Эйлера для стали марки Ст3, для которой модуль упругости Е = 2,110⁵ МПа. Из графика видно, что при возрастании гибкости стержня критическое напряжение стремиться к нулю и, наоборот, по мере приближения гибкости к нулю критическое напряжение увеличивается.

Однако вывод формулы Эйлера был построен на предположении, что напряжения в стержне не превышают предела пропорциональности: , откуда предельное значение гибкости: .

Значит формула Эйлера непригодна для стержней с гибкостью меньшей _пр. Например, для стали марки Ст3 формула Эйлера становится непригодной, если: .

То же значение можно получить, рассматривая график гиперболы Эйлера (рис. 10.8).

Потеря устойчивости может происходить и при напряжениях, превышающих предел пропорциональности. Опытным путем было установлено, что для стержней с гибкостью меньше _пр действительные критические напряжения ниже критических напряжений, определенных по формуле Эйлера. Поэтому использование формулы Эйлера для стержней, теряющих устойчивость за пределом пропорциональности, не только принципиально неправильно, но и крайне опасно.

Что бы определить значения критических напряжений для стержней с гибкостью меньше _пр проводились многочисленные испытания. На основании результатов экспериментальных исследований Ф. Ясинский предложил эмпирическую формулу, показывающую, что критические напряжения при таких гибкостях меняются по закону, близкому к линейному: , г

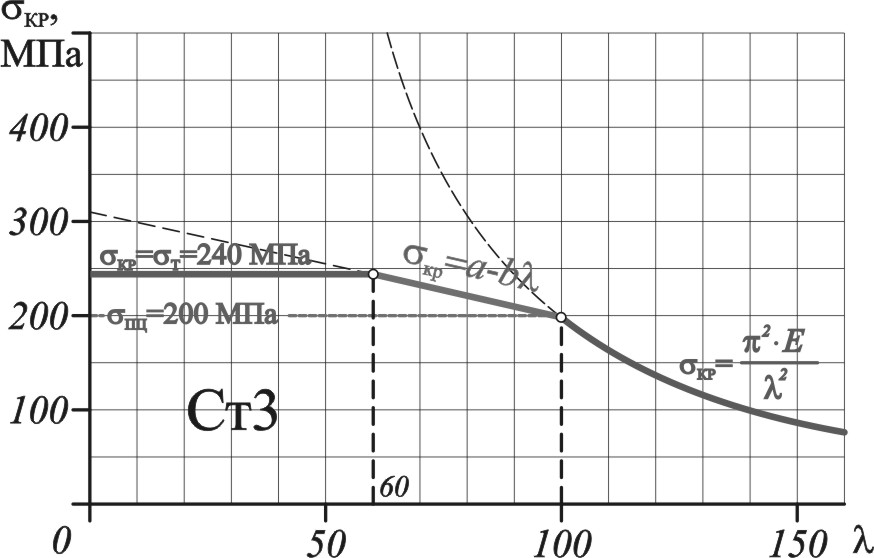
Рисунок 10.9

де a и b  величины, зависящие от материала; их значения приводятся в справочниках.

Например, для стали марки Ст3 значения данных коэффициентов составляют а = 310 МПа; b = 1,14 МПа.

На рис. 10.9 пунктиром показана прямая, уравнение которой соответствует выражению (10.8). Очевидно, что с правой стороны данная прямая ограничивается гиперболой Эйлера.

При некотором значении гибкости (обозначим его ₀) величина _кр становиться равной предельному напряжению при сжатии: ⁰ = _т  для пластичных материалов или ⁰ = _в  для хрупких материалов. Стержни, у которых  < ₀, называют стержни малой гибкости. Их рассчитывают только на прочность.

Таким образом, для стали марки Ст3 график _кр = f()состоит из трех частей: гиперболы Эйлера при  > 100, наклонной прямой при 60 <  < 100 и горизонтальной прямой при  < 60. Горизонтальная прямая соответствует пределу текучести.

Билет46 Понятие о динамическом действии нагрузки

Ранее во всех рассмотренных нами задачах предполагалось, что действующие нагрузки статические, т.е. не изменяющиеся с течением времени. При проектировании машин обычно сталкиваются с деталями, находящимися в неравномерном движении, что приводит к появлению инерционных нагрузок.

Примером статической нагрузки, или статического действия нагрузки, может послужить действие подвешенного на цепи груза. Это действие остается статическим, если груз будет подниматься цепью с постоянной скоростью. Но тот же груз, поднимаемый цепью с ускорением, будет действовать на цепь динамически. Для расчета цепи в данном случае мы должны учесть не только вес груза, но и силу инерции груза.

Д

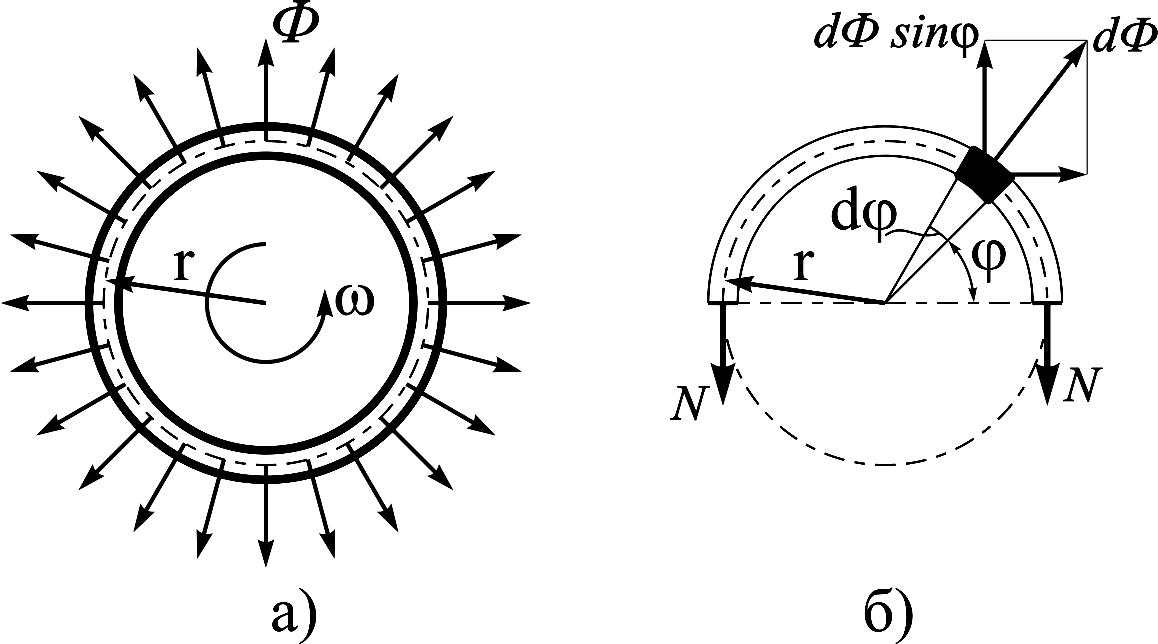
Рисунок 11.1

ля примера рассмотрим расчет равномерно вращающегося тонкого кольца (рис. 11.1, a).Для расчета примем следующие обозначения: r  средний радиус кольца; F  площадь поперечного сечения;   удельный вес материала;   угловая скорость кольца; g  ускорение силы тяжести.

Рассмотрим бесконечно малый элемент кольца массой dm, вырезанный двумя плоскостями, составляющими центральный угол d (рис. 11.1, б)

Элементарная сила инерции dФ: . Элементарная масса, выраженная через площадь сечения кольца: .

Элементарная сила инерции с учетом (11.2) будет равна: Для определения продольной силы N в поперечном сечении кольца рассмотрим равновесие половины кольца под действием двух продольных сил N и суммы вертикальных составляющих элементарных сил инерций: , откуда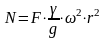 . (11.4)

Полагая, что в тонком кольце все волокна растягиваются одинаково, найдем напряжение в сечении кольца: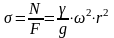 . Определим теперь, на сколько удлинится радиус вращающегося кольца. Относительное удлинение волокон кольца равны: .Из закона Гука: .Откуда . (11.6)