Билет 9-12) Геометрические характеристики плоских сечений

Площадь: , dF — элементарная площадка.

С татический момент элемента площади dF относительно оси 0x — произведение элемента площади на расстояние "y" от оси 0x: dS_x = ydF

Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и X: ; [см3, м3, т.Д.].

Координаты центра тяжести: . Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями F_i и координатами центров тяжести x_i, y_i.Статический момент площади всей фигуры = сумме статических моментов каждой ее части: .

Координаты центра тяжести сложной фигуры:

Моменты инерции сечения

О севой (экваториальный) момент инерции сечения — сумма произведений элементарных площадок dF на квадраты их расстояний до оси.

; [см⁴, м⁴, т.д.].

Полярный момент инерции сечения относительно некоторой точки (полюса) — сумма произведений элементарных площадок на квадраты их расстояний от этой точки. ;[см⁴, м⁴,т.д.].J_y + J_x = J_p .

Центробежный момент инерции сечения — сумма произведений элементарных площадок на их расстояния от двух взаимно перпендикулярных осей. .

Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с осями симметрии, равен нулю.

Осевые и полярные моменты инерции всегда положительны, центробежные моменты инерции могут быть положительными, отрицательными или равными нулю.

Момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.

Билет 12)Моменты инерции сечений простой формы

П рямоугольное сечение Круг

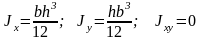
К ольцо

Т реугольник

р авнобедренный

Прямоугольный

т реугольник

Ч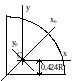 етверть круга

J_y=J_x=0,055R⁴

J_xy=0,0165R⁴

на рис. (—)

J_x0=0,0714R⁴

J_y0=0,0384R⁴

Полукруг

М оменты инерции стандартных профилей находятся из таблиц сортамента:

Д вутавр Швеллер Уголок

М

оменты инерции относительно параллельных осей:

J _x1=J_x + a²F;

J_y1=J_y + b²F;

момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. J_y1x1=J_yx + abF; ("a" и "b" подставляют в формулу с учетом их знака).

Понятие о радиусе инерции

Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции:

(3.24)

где  радиус инерции относительно оси х.

Из выражения (3.24) следует, что

. (3.25)

Аналогично радиус инерции площади сечения относительно оси :

. (3.26)

Главным центральным осям инерции соответствуют главные радиусы инерции:

, .

Моменты сопротивления площади

Осевым моментом сопротивления площади сечения F относительно главной центральной оси называется отношение момента инерции площади относительно этой же оси к расстоянию до наиболее удаленной точки от этой оси:

. (3.28)

Момент сопротивления измеряется в м³.

Отношение полярного момента инерции площади сечения к наибольшему радиусу  вектору этой площади, называется полярным моментом сопротивления:

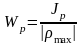. (3.29)

Для площади прямоугольника:

, .

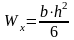Для площади круга:

, , .

Б илет 13)Зависиомсть между моментами инерции относительно параллельных осей

Пусть х_с, у_с  центральные оси сечений,  моменты инерции сечения относительно этих осей. Определим моменты инерции сечения относительно новых осей х₁, у₁, параллельных центральным осям и смещенных относительно них на расстояния а и d. Пусть dF  элементарная площадка в окрестности точки М с координатами х и у в центральной системе координат. Из рис. 3.5 видно, что координаты точки в новой системе координат будут равны:

.

Определим момент инерции сечения относительно оси х₁:

.Очевидно, что первый интеграл дает , второй  , т.к. исходная система координат  центральная, а третий  площадь сечения F. Таким образом,

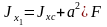. (3.10)

Аналогично,

, (3.11)

. (3.12)

Билет14) Изменение моментов инерции п

Рисунок 3.10

ри повороте осей координат.

Пусть задана система координат и известны моменты инерции J_х, J_у и J_хy фигуры относительно осей координат. Повернем оси координат на некоторый угол  против часовой стрелки и определим моменты инерции той же фигуры относительно новых осей и и v (рис. 3.10).

Координаты точки в этих системах координат связаны уравнениями:

.

Момент инерции:

,

или

, (3.19)

и

, (3.20)

Центробежный момент инерции:

, (3.21)

Из полученных уравнений видно, что , т.е. сумма осевых моментов инерции при повороте осей координат остается величиной постоянной. Поэтому, если относительно какой-либо оси момент инерции достигает максимума, то относительно перпендикулярной ей оси он имеет минимальное значение.

Билет 15) Главные оси и главные моменты инерции сечения

Оси, относительно которых центробежный момент инерции сечения обращается в нуль, называются главными осями, а главные оси, проходящие через центр тяжести сечения  главными центральными осями инерции сечения.

Моменты инерции относительно главных осей инерции сечения называются главными моментами инерции сечения и обозначаются J₁ и J₂ причем J₁ > J₂.

Предположим, что оси и и v главные. Тогда

,

, (3.22)

Уравнение (3.22) определяет положение главных осей инерции сечения в данной точке относительно исходных осей координат. При повороте осей координат изменяются также и осевые момента инерции. Найдем положение осей, относительно которых осевые моменты инерции достигают экстремальных значений. Для этого возьмем первую производную от J_u по  и приравняем ее нулю:

,

тогда

.

К тому же результату приводит и условие . Сравнивая последнее выражение с формулой (3.22), можно сделать вывод, что главные оси инерции являются осями, относительно которых осевые моменты инерции сечения достигают экстремальных значений.

Исключая из формул (3.19), (3.20), (3.21) тригонометрические функции, получим:

. (3.23)

Знак плюс в формуле (3.23) соответствует большему (J₁), а знак минус  меньшему (J₂) моментам инерции сечения.

Нетрудно доказать, что если моменты инерции сечения относительно главных осей одинаковы, то все оси, проходящие через ту же точку сечения, являются главными и осевые моменты инерции относительно всех этих осей одинаковы: J_u = J_v = J_y = J_х. Этим свойством обладают квадратные, круглые и кольцевые сечения