
- •Понятие ф-и и способы ее задания
- •Функции в экономике
- •Вопрос 4. Числовая последовательность и ее пределы.
- •Вопрос 5. Предел функции, основные теоремы о пределах.
- •Вопрос 6. 1ый и 2ой замечательные пределы.
- •7.Бесконечно малые, бесконечно большие величины
- •8.Непрерывность функций. Точки разрыва, их классификация.
- •13. Производная и дифференциал высшего порядка.
- •14. Экономический смысл производной и понятие эластичности.
- •15. Приложение производной.
- •5.Теорема(правило) Лопиталя.
- •Вопрос 22 Экстремумы
- •Вопрос 23 Метод наименьших квадратов
- •24 Вопрос Неопределенный интеграл, свойства
- •25.Методы интегрирования неопред. Интеграла.
- •1. Непосредственное интегрирование.
- •2.Интегрирование по частям
- •3.Метод замены переменной
- •4.Интегрирование рациональных дробей.
- •27.Методы интегрирования определенноно интеграла.
- •28. Несобственные интегралы.
- •29. Дифференциальные уравнения.
- •30. Решение дифференциальных уравнений.
Понятие ф-и и способы ее задания
Постоянная величина-величина,сохраняющая свое значение(число пи). Параметром называется величина,кот. сохраняет свое постоянное значение лишь в условиях данного процесса. Переменной называется величина,кот. может принимать различные числовые значения. Пусть заданы 2 числ.мн-ва Х и У. если каждому элементу мн-ва Х ставится в соответствие вполне определ.знач. У, то говорят,что на мн-ве Х задана ф-я: у=f(x)х-аргумент,у-зависимая переменная,f-закон соответствия.мн-во Х – область определения ф-и, мн-во У – область значений ф-и. способы задания:1) табличный.2)аналитический(ф-я задается с помощью формулы).3)графический(график функци – мн-во на оордин.плоскости).4)словесный(ф-я описывается правилом ее составления).
Основные элементарные ф-и и их св-ва.

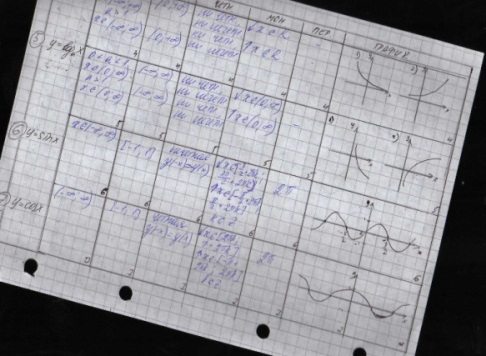
Функции в экономике
Наиболее
часто в эк-ке используются:1)ф-я
полезности(предпочтений) – это
зависимость результата эффекта
некоторого действия от интенсивности
этого действия.2)производственная –
результат произв.деятельности от
обусловивших его факторов.3)ф-я выпуска
– зависимость объема пр-ва от наличия
или потребления ресурсов(частный случай
ф-и 2).4)ф-я издержек – это зависимость
издережек пр-ва от объема выпуска
продукции(частный случай ф-и 2).5)ф-я
спроса,потребления,предложения –
зависимостьобъема спроса,потрбл.,предл
на отдельные товары и услуги от различных
факторов(цены,дохода и др.). Примеры
использования этих ф-й: 1)исследуя
зависимость спроса на различн.товары
от дохода, можно установить уровни
доходов,при кот. начинается потребление
товаров и уровни насыщения на товары1й,2й
необходимости и предметы роскоши.
Функции Торнквиста: y1=b1*(x-a1)/(x-c1)
x>a1
– 1я необходимость; y2=b2*(x-a2)/(x-c2)
x>a2
– 2я необходимость; y3=b3*(x-a3)/(x-c3)
x>a3
– роскошь; а1,а2,а3 – уровни доходов;
b1,b2,b3
– уровни насыщения. На этом графике
заменить D3=b3,
D2=b2,D1=b1
и I1=a1,I2=a2,I3=a3.
I
– доходы, D
– объем спроса.
2 )рассматривая
в одной системе координат ф-и спроса и
предложения, можно установить
равновеснцю(рыночную) цену данного
товара в процессе формирования цен в
условиях рыночной экономики.3)изучая
в теории потребления и спроса кривые
безразличия(линия, вдоль которой
полезность 2х благ одна и та же),например
заданные в виде xy=U
и линию бюджетного ограничения
px*x+py*y=I
при ценах благ px
и py
и доходе потребления I
можно установить оптимальное количество
благ x0,y0,
имеющих максимальную полезность
U0.4)рассматривая
ф-и издержек и дохода фирмы,можно
установить зависимость прибыли от
объема прва q.
П(q)=C(q)-r(q),
также можно выявить уровни q
, при которых пр-во убыточно, приносит
прибыль, дает макс.убыток или
макс.прибыль;также можно определить
размеры убытков и прибыли.
)рассматривая
в одной системе координат ф-и спроса и
предложения, можно установить
равновеснцю(рыночную) цену данного
товара в процессе формирования цен в
условиях рыночной экономики.3)изучая
в теории потребления и спроса кривые
безразличия(линия, вдоль которой
полезность 2х благ одна и та же),например
заданные в виде xy=U
и линию бюджетного ограничения
px*x+py*y=I
при ценах благ px
и py
и доходе потребления I
можно установить оптимальное количество
благ x0,y0,
имеющих максимальную полезность
U0.4)рассматривая
ф-и издержек и дохода фирмы,можно
установить зависимость прибыли от
объема прва q.
П(q)=C(q)-r(q),
также можно выявить уровни q
, при которых пр-во убыточно, приносит
прибыль, дает макс.убыток или
макс.прибыль;также можно определить
размеры убытков и прибыли.
Вопрос 4. Числовая последовательность и ее пределы.
Числовая последовательность – совокупность чисел(конеч.,бесконеч.), заданная по опред.gравилу. {аn} или (аn) чп – функци натурального аргумента. Входящие числа – элементы или члены. аn – общий член последовательности. Может быть задана:
- перечислением элементов 2,4, 6…2n
-
аналитически 1) аn =
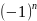 n!
формула n члена 2) а1 задать аn(задаетсячерез
аn-1) рекурентный способ задания
последовательности.
n!
формула n члена 2) а1 задать аn(задаетсячерез
аn-1) рекурентный способ задания
последовательности.
Предел последовательности. А называют пределом последовательности (Хn), если сущ.Е>0 найдется такой номер N, что для всех n>N выполняется /Xn-a/<Е
а
=
 Если число а конечное, то послед
сходящаяся, если число а бесконечное,
то послед.расходящаяся.
Если число а конечное, то послед
сходящаяся, если число а бесконечное,
то послед.расходящаяся.
эпселонт окрестности /Xn-a/<Е -Е< Xn-a <Е а-Е < Xn < а+Е
геометрический смысл предела. а – предел числ.послед., если сущ Е>0 найдется N, начиная с кот.все члены послед.будут заключены в Е-окрестности точки а , какой бы узкой она не была. За пределами Е-окр. Находится конечное число Е – последовательности.
