53. Потенциальное поле. Независимость интеграла от пути интеграции.

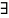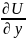Опр. Векторное поле =(P,Q,R) назыв. потенц. на обл-ти в , если U=U(x,y,z), которая опред. на обл-ти , имеет непрерывные частные производные 1 порядка и =grad U на Ω,т.е. P= , Q= , R= .Ф-ия U-назыв. потенциалом вектора поля а.

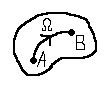
Th. Пусть векторн. поле назыв. потенциальной на обл-ти Ω с потенц. U и пусть A,B – любые две фикс. точки из обл-ти , тогда криволин. интег. 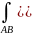,d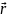 ) по любом пути соед. А и В не завис. от выбора пути и вычисл. по ф-ле ,d )=U(B)-U(A) (1)

54. Критерии потенциальности

Th1: Чтобы непр. век. поле было потенц. на обл. , необх. и дост., чтобы для  контура Г, котор явл. кус. гл. и целиком лежит в , циркуляция поля по Г:

Опред: Обл.  в -односвязная, если для  замкнут. кус. гл. контура Г, лежащ. в , существует пов-ть S, также лежащ в , границей котор. явл. Кривая Г.

Th2: Для того, чтобы непр. дифф. век. поле на односвяз. обл.  было потенц., необх. и дост., чтобы оно было безвихревым, т.е rot =0 на .

Опред: Непрерывное дифференцируемое векторное поле в -соленоидальное, если div =0.

55. Сходящиеся и расходящиеся числовые ряды. Критерий Коши сходимости ряда. Необходимое условие сходимости.

Пусть есть посл-ть составим выражение (1) Такое выражение будем наз-ть рядом. - член ряда.

частичная сумма ряда.

Опр. Числов. Ряд (1) наз-ся сходящимся, если сходится посл-ть 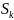частичных сумм этого ряда. Предел 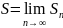наз-ся суммой ряда Если посл-ть частичных сумм не имеет предела, то говорят, что ряд расходится.

Св-ва рядов связанные со сход-тью:

1 св-во: Прибавление к ряду конечного числа членов или отбрасывание конечного числа членов ряда не влияет на сходимость ряда.

2 св-во: Пусть дан некоторый ряд и пусть c –const . Тогда ряд 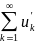сх-ся тогда, и только тогда, когда сх-ся ряд и вып-ся рав-во

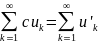
3 св-во: Если ряды и 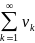сх-ся то их сумма и разность тоже сходится и равна .

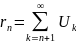Следствие 1. Если ряд сх-ся то тогда посл-ть явл-ся беск малой. 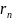- n-ный остаток ряда. Посл-ть б.м. , значит для такое что для Это вытекает из (2) которое справедливо при а так же из теор о переходе к пределу в неравенствах.

Следствие 2. Необх.усл. сх-ти ряда. Для того, что бы ряд сходился, необходимо что бы

56. Признаки сравнения.

Тh1. Для того что бы числовой ряд с неотриц. элементами сходился, необходимо и достаточно, что бы посл-ть част-ных сумм этого ряда была ограниченной.

Тh2. Если и ряды с неотриц.членами, и для всех к выполняется (1) то из сх-ся ряда следует сх-ть ряда , а расходимость ряда влечет рас-ть .

Замечание 1 Тh2 остается справедливой, если (1) выполняется не для всех к, а лишь начиная с некоторого номера.

Замечание 2 Тh2 остается справедливой, если вместо (1) написать нер-во 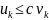где 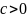–конст. В силу 2ого св-ва сх-ся ряда, ряд 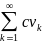сх-ся, когда сх-ся

Следствие к Тh2 Если ряд с неотриц членами, ряд с полож-ми членами и если 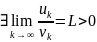(3) то тогда ряды и , сх-ся или расх-ся одновременно