20 Этапы проектирования кулачкового механизма

– выбор кинематической схемы;

– выбор закона движения толкателя;

– построение кинематических характеристик толкателя в зависимости от угла поворота кулачка и времени;

– определение основных параметров механизма по допустимому углу давления или другим условиям, например выпуклости профиля кулачка;

– построение теоретического профиля кулачка;

– определение радиуса ролика или длины плоского толкателя;

– построение действительного профиля кулачка.

При выполнении курсового проекта не производится выбор кинематической схемы, так как она содержится в задании на проект. Закон движения толкателя обычно указан в исходных данных.

Проектирование кулачкового механизма можно осуществлять графическим или численным методом. При графическом методе проектирования все построения выполняются в масштабе на чертежном листе.

Рис. 8.2. Основные схемы кулачковых механизмов:

а – с поступательно движущимся толкателем с роликом; б – с коромысловым толкателем с роликом; в – с поступательно движущимся плоским толкателем.

21 Условие передачи сил

Качество передачи сил в машинах принято характеризовать углом давления λ, определенным без учета сил тяжести звеньев и сил инерции.

Угол давления λ – это острый угол между вектором силы, действующей на ведомое звено со стороны смежного с ним подвижного звена, и вектором абсолютной скорости точки приложения этой силы.

Угол передачи движения γ дополняет угол давления до 90°:

γ = 90° – λ .

На стадии метрического синтеза ограничивают предельно допустимые углы давления [λ _max] и передачи движения [γ_min], как правило, принимая их:

[λ _max] ≤ 30° и [γ_min] ≥ 60° для поступательно движущегося ведомого звена, и

[λ _max] ≤ 40°...45° и [γ_min] ≥ 50°...45° – для вращающегося ведомого звена.

22 Рассмотрим условие передачи сил в шарнирном четырехзвеннике, находящемся в равновесии под действием моментов движущего М_Д и момента сопротивления М_С (рис. 3.1). Угол давления λ характеризует соотношение между полезной силой сопротивления F₂₃ cos λ , преодолевающей момент сопротивления М_С , и силой F₂₃ , равной F₂₃ = М_С /(l_ВС ∙ cos λ).

Рис.3.1. Угол λ давления в шарнирном четырехзвеннике

С увеличением угла давления необходимо прикладывать большую силу F₂₃ для преодоления одного и того же момента сопротивления. Это ведет к увеличению реакций в кинематических парах и снижению КПД механизма.

При движении механизма угол давления меняется. Экстремальных значений этот угол в шарнирном четырехзвеннике достигает в положениях, когда кривошип ОА располагается на одной прямой со стойкой ОС.

В кривошипно-ползунном механизме угол давления приобретает экстремальные значения в положениях, когда кривошип ОА перпендикулярен траектории движения ползуна В.

23 Построение профиля кулачка

Построение профиля кулачка производится с использованием метода обращенного движения: кулачок на чертеже считают неподвижным, а стойку – вращающейся со скоростью, равной по модулю и противоположной по направлению угловой скорости кулачка.

При профилировании кулачка необходимо обратить внимание на использование крупных масштабов, детальный показ всех линий построения и строгую нумерацию всех точек, используемых при вычерчивании кулачка. На чертеже необходимо выделить утолщенными линиями кинематическую схему механизма, указать теоретический и действительный профили кулачка. Для поступательно перемещающихся толкателей на схеме механизма изобразить направляющую толкателя.

Для толкателей с роликом радиус r_рол ролика рассчитать по нижеследующим формулам:

r_рол = (0,6...0,8) ρ_min ; r_рол = (0,25...0,3) r_min ,

где ρ_min и r_min – соответственно минимальный радиус кривизны и минимальный радиус–вектор теоретического профиля кулачка. Для построения принять наименьшее значение.

24 Для передачи вращательного движения в машинах от входного вала к выходному часто используются передаточные зубчатые механизмы. Передаточным отношением механизма от его входного вала 1 к выходному валу <вых> называют отношение угловых скоростей ω или частот n вращения этих валов:

u_1−вых = ω₁/ω _вых = n₁/n _вых .

Планетарные зубчатые механизмы по сравнению с другими обладают меньшим весом и габаритными размерами.

25 ДИФФЕРЕНЦИАЛЬНЫЙ механизм - механизм, в котором результирующее перемещение равно сумме или разности исходных перемещений, напр. зубчатые механизмы в транспортных машинах, обеспечивающие вращение ведущих колес с различными скоростями на поворотах.

Планетарным называется дифференциальный механизм, если в нем одно из звеньев неподвижно. Планетарные механизмы используются:

1) в планетарных редукторах;

2) в планетарных механизмах включения и выключения;

3) в планетарных реверсивных механизмах;

4) в планетарных коробках передач;

5) в планетарных вариаторах, обеспечивающих бесступенчатое изменение величины

передаточного отношения в больших пределах. Все эти механизмы надежны и легко

управляемы, создают широкие возможности для их использования

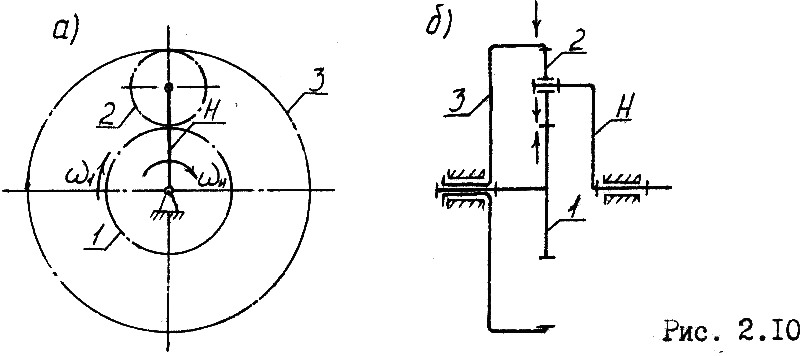
Получим формулу, связывающую угловые скорости звеньев в дифференциальном механизме. Используем метод обращения движения. Сообщаем всем звеньям механизма дополнительную угловую скорость, равную угловой скорости водила Н, но противоположно направленную, т.е. (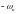 ). При этом относительное движение звеньев не изме­нится, а угловые скорости в обращенном движении будут следующи­ми:

Таким образом, так как 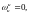то дифференциальный меха­низм превратился в зубчатый механизм с неподвижными осями. Для такого обращенного механизма

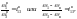(2.6)

где - передаточное отношение обращенного механизма, опре­деляемое через число зубьев колес:

Полученное выражение(2.6) называется формулой Виллиса.

26 Для постоянства передаточного отношения при зацеплении двух профилей зубьев необходимо, чтобы радиусы начальных окружностей зубчатых колёс, перекатывающихся друг по другу без скольжения, оставались неизменными. Если рассмотреть обращённое движение начальных окружностей, когда всей системе задана угловая скорость ( ), то второе колесо будет условно неподвижным и точка Р является мгновенным центром относительного вращения колёс (рис. 70,а). Эта точка, называемая полюсом зацепления, где контактируют начальные окружности, делит межцентровое расстояние на отрезки, обратно пропорциональные угловым скоростям, т. к.

                          .

Рассмотрим обращённое движение профилей зубьев зубчатых колёс (рис. 70, б).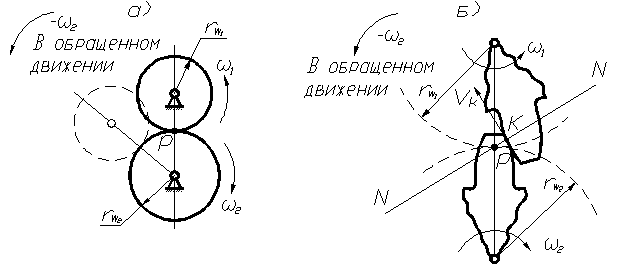

рис. 70

Точка контакта зубьев (точка к), принадлежащая первому колесу, вращается вокруг точки Р, которая будет мгновенным центром скоростей. Скорость   и совпадает с общей касательной к профилям в точке к при условии постоянства этого контакта.

рис. 71                  

В противном случае постоянного контакта не будет, так как появится составляющая   и профили разомкнутся. Так как рассматривается произвольное положение зубьев, то можно сформулировать теорему. 

     Нормаль  NN  к  касающимся  профилям  зубьев, проведённая  через  точку их касания, делит   межцентровое  расстояние на части, обратно пропорциональные угловым скоростям.

Эта теорема, сформулированная Виллисом в 1841 г., определяет основной закон зацепления профилей, которые не могут быть произвольными, а должны быть специально подобраны

27 Эвольвента - это кривая, описываемая любой точкой прямой, перекатываемой без скольжения по неподвижной окружности.

Эвольвента имеет следующие свойства: 1) начинается с основной окружности; 2) нормаль к эвольвенте является касательной к основной окружности;3) радиус кривизны эвольвенты в каждой её точке лежит на нормали к эвольвенте в этой точке.

Параметрические уравнения эвольвенты окружности:

где  — радиус окружности;  — угол поворота радиуса окружности.

28 Эвольвентное зацепление позволяет передавать движение с постоянным передаточным отношением. Эвольвентное зацепление — зубчатое зацепление, в котором профили зубьев очерчены по эвольвенте окружности.

Для этого необходимо чтобы зубья зубчатых колёс были очерчены по кривой, у которой общая нормаль, проведённая через точку касания профилей зубьев, всегда проходит через одну и ту же точку на линии, соединяющей центры зубчатых колёс, называемую полюсом зацепления

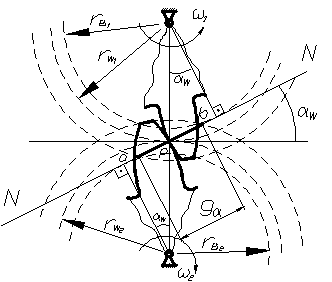
В процессе зацепления зубья касаются друг друга различными точками профиля. Так как эти точки лежат на нормали к профилям, которая одновременно является касательной к обеим основным окружностям, то совокупность точек касания (линия  ) совпадает с общей для обеих основных окружностей касательной NN. Эта линия называется теоретической линией зацепления, а линия   длиной g_α является её активной частью, где располагаются все точки контакта зубьев. Угол  , измеряемый между нормалью  NN  к  профилям  в полюсе зацепления Р и общей касательной к обеим начальным окружностям, называется углом зацепления. Таким образом:

   

29 Дуга зацепления L - путь по начальной окружности, проходимый точкой профиля зуба за время его фактического зацепления; или, иначе, - дуга начальной окружности, на которую пара сопряженных зубьев поворачивает колесо. Дуга зацепления определяется положениями профиля зуба в начале и конце зацепления.

Коэффициент перекрытия определяет величину зоны двухпарного контакта, когда одновременно зацепляются два последовательно расположенных зуба. Так как до окончания зацепления одной пары зубьев, следующая пара должна войти в контакт, нельзя допускать в прямозубых передачах  . Допустимое значение коэффициента перекрытия должно несколько превышать единицу и, в зависимости от назначения передачи и точности ее изготовления, выбирается в пределах  . Наиболее благоприятны величины коэффициента перекрытия равные целым числам, например двум или трем. Обеспечить это можно только используя инструмент с нестандартным исходным производящим контуром. Дробные значения коэффициента перекрытия, например близкие к полутора, приводят к циклическому изменению жесткости передачи и к возникновению параметрических колебаний. Торцовый коэффициент перекрытия

.

* Для нормальной работы зубчатой передачи должно быть выполнено условие: ε ≥ 1,05.

30 Прямозубые колёса — самый распространённый вид зубчатых колёс. Зубья расположены в радиальных плоскостях, а линия контакта зубьев обеих шестерён параллельна оси вращения. При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, но, в то же время, предельный крутящий момент таких колес ниже, чем косозубых

Косозубые колёса являются усовершенствованным вариантом прямозубых. Их зубья располагаются под углом к оси вращения, а по форме образуют часть спирали.

Достоинства:

Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом.

Площадь контакта увеличена по сравнению с прямозубой передачей, таким образом, предельный крутящий момент, передаваемый зубчатой парой, тоже больше.

Недостатками косозубых колёс можно считать следующие факторы:

При работе косозубого колеса возникает механическая сила, направленная вдоль оси, что вызывает необходимость применения для установки вала упорных подшипников;

Увеличение площади трения зубьев (что вызывает дополнительные потери мощности на нагрев), которое компенсируется применением специальных смазок.

В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.