10 Силовой расчет группы Ассура 2-го класса 2-го вида

Группа второго вида имеет одну внешнюю поступательную пару C с направляющей x-x Требуется определить _1-2, _3-2, _0-3 и плечо силы _0-3 относительно точки B.

Для реакции _1-2 известна точка ее приложения, неизвестными являются направление и величина. Реакция перпендикулярна к оси x-x направляющей. Неизвестными являются точка ее приложения и величина.

Величину составляющей F ^τ_1-2 определим из условия равновесия моментов сил, действующих на звено 2 относительно точки В:

∑ M_{B (звена 2)} = –M₂ + M_B(F₂) – F ^τ_1-2 l_AB = 0,

откуда

F ^τ_1-2 = [–M₂ + M_B(F₂)] / l_AB .

Рассмотрим равновесие сил, действующих на группу Ассура:

.

Плечо h силы _0-3 относительно точки B определим из следующего условия равновесия моментов, действующих на звено BC относительно точки B (рис. 6.4):

∑ M_{B (звена 3)} = M₃ – M_B(F₃) + F _0-3 h = 0,

откуда h = [M_B(F₃) – M₃] / F _0-3 .

11 Силовой расчет группы Ассура 2-го класса 3-го вида

Группа Ассура 2-го класса 3-го вида.Заданы силы F₂ и F₃, а также пары сил с моментами M₂ и M₃, действующие на звенья.

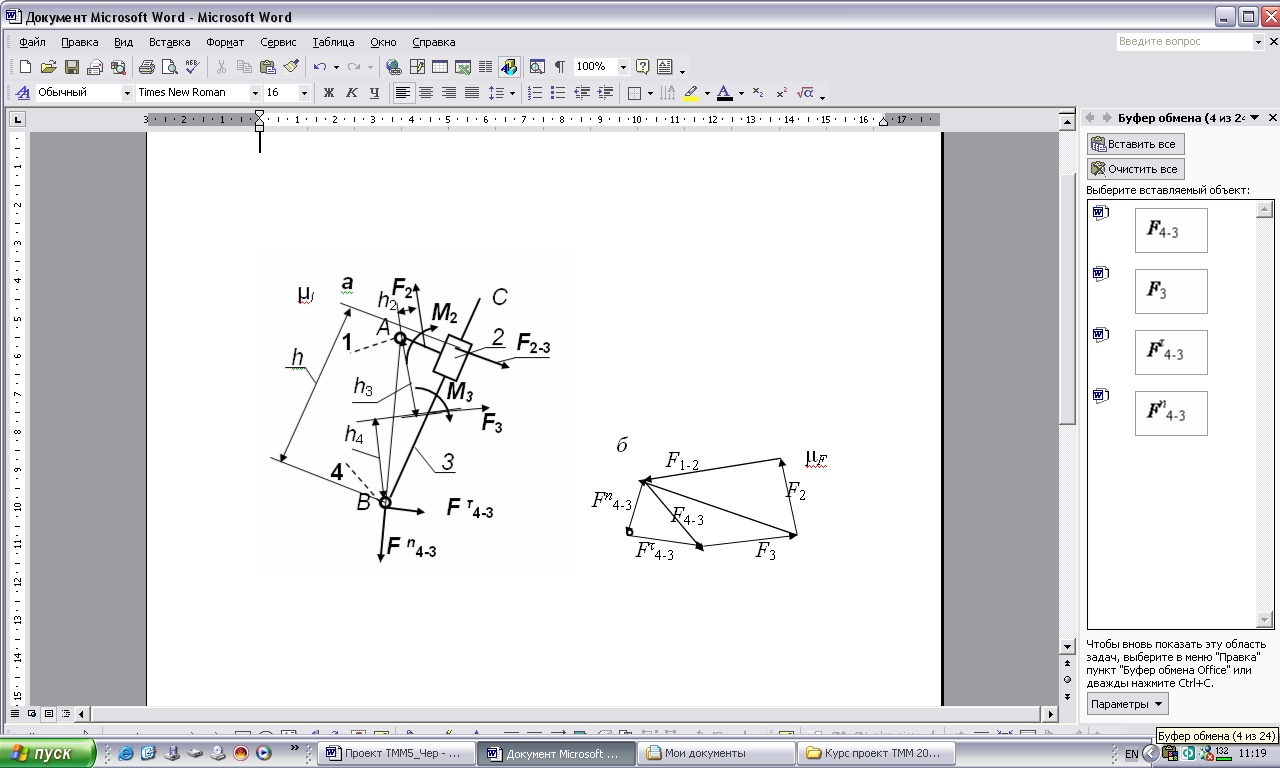
ΣМ_{А (гр. Ассура)}= −М₂ − М₃ + F₂ h₂ μ_l + F₃ h₃ μ_l + F ^τ_4-3 l_АВ = 0.

Откуда

F ^τ_4-3 = (М₂ + М₃ − F₂ h₂ μ_l − F₃ h₃ μ_l ) / l_АВ .

Из условия равновесия векторов сил, действующих на звено 3, имеем

Σ _{(Звена 3)}= ^τ_4-3 + ₃ + _2-3 + ⁿ_4-3 = 0.

Плечо h приложения силы _2-3 найдем из следующего уравнения:

ΣМ_{В (звена 3)}= − М₃ −F₃ h₄ μ_l − F_2-3 h = 0.

Откуда

h = (− М₃ −F₃ h₄ μ_l) / F_2-3 .

12 Кинетостатика начального звена

В результате силового расчета всех групп, образующих механизм, была определена сила _1-2 воздействия кривошипа на смежное с ним звено.2. Сила действия звено 2-го звена на кривошип 1 равна

_2-1 = – _1-2.

Движение начального звена 1 рабочей машины осуществляется двигателем через пару зубчатых колес (рис. 6.7, а), или при помощи муфты (рис. 6.7, б). воздействие привода на кривошип осуществляется уравновешивающей силой _y, приложенной в полюсе зацепления P под углом зацепления α,

Звено вращается с угловым ускорением ε₁. На это звено действуют следующие силы: сила F_2-1, приложенная в точке А, уравновешивающая сила _y, приложенная в полюсе Р зацепления колес, реакция стойки F_0-1, приложенная в точке О. Кроме того, на него действуют сила веса G₁ звена, сила инерции F_и1, приложенные в центре масс S₁ звена 1, и момент сил инерции М_и1. Неизвестными являются силы _y и _0-1.

Уравновешивающую силу определяем из уравнения равновесия ведущего звена, приравняв к нулю сумму моментов всех сил относительно точки O:

∑М_О = М_и + μ_S (– F_2-1 h₁ – G₁ h₃ + F_и1 h₂ + F_у h_у) = 0.

Откуда F_у = [ F_2-1 h₁ + G₁ h₃ – F_и1 h₂ ) – (М_и / μ_S )] / h_у .

Для определения F_0-1 построим план сил (рис. 6.8,б) в соответствии с векторным уравнением, соблюдая масштабный коэффициент μ_F :

∑ = _у + ₁ + _2-1 + _и1 + _0-1 =0.

13 Задачей силового расчета является определение сил, действующих на звенья механизма, и сил взаимодействия этих звеньев, т. е. реакций во всех кинематических парах. Зная реакции, можно в дальнейшем выполнить расчет звеньев на прочность и выбрать подшипники. Кроме этого, при силовом расчете определяется сила, действующая со стороны привода на ведущее звено.

При силовом расчете пользуются принципом Даламбера. Согласно этому принципу, если к звеньям механизма приложить активные силы и моменты пар сил, а также силы инерции и моменты пар сил инерции, то можно условно считать, что система сил находится в равновесии и к ней применимы уравнения статики. Этот принцип носит еще одно название – принцип кинетостатики.

Сила инерции прикладывается к центру звена S и направлена в сторону, противоположную направлению полного ускорения точки S.

,

где − вектор сил инерции звена, Н; m − масса звена, кг; a_s − вектор абсолютного ускорения центра тяжести звена, м/с².

Момент пары сил инерции M_и, направлен в сторону, противоположную направлению углового ускорения звена и равен

,

где I_s − момент инерции звена относительно оси, проходящей через центр тяжести S, перпендикулярной к плоскости движения звена, измеряемый в кг·м².

15 необходимо по заданным условиям рассчитать размеры звеньев проектируемого механизма, произвести структурный анализ, определить аналоги скоростей звеньев, параметры динамической модели и закон движения начального звена рычажного механизма.

Графическая часть состоит из построения планов механизма в двенадцати положениях, планов скоростей, диаграмм динамической модели и закона движения начального звена.

Режимы движения машины

На рис. 5.2 показана графическая зависимость скорости ω на­чального звена механизма с одной степенью свободы от времени t. Полное время движения машины можно разделить на три участка, соответствующих следующим режимам движения.

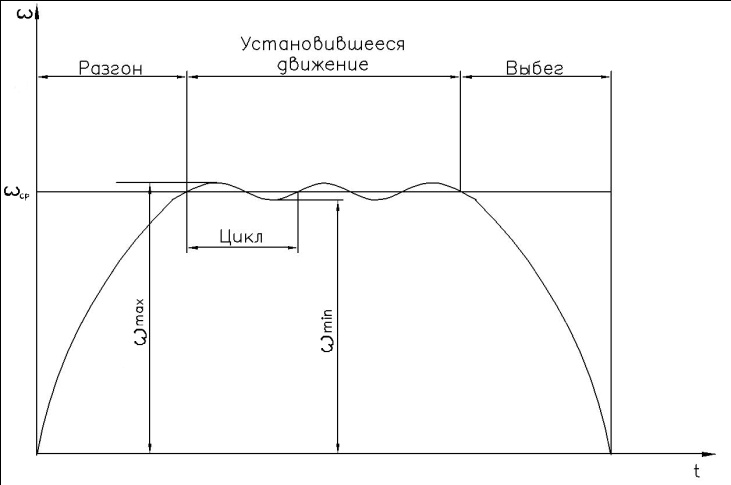
Разгон, в процессе которого происходит постепенное возрас­тание скорости начального звена от нуля до среднего значения ω_ср. А_D > A_C.

При установившемся движении скорость начального звена периодически изменяется около одного и того же среднего значения ω_ср. Минимальный промежуток времени, по истечении которого начальное звено возвращается в первоначальное положение, называется циклом установившегося движения. А_D = A_C .

Выбег характеризуется постепенным уменьшением скорости начального звена от среднего значения ω_ср до нуля. А_D < A_C .

Для машин, в которых преобладает установившийся ре­жим движения, одним из критериев работоспособности является коэффициент δ неравномерности установившегося движения

δ = (ω_max − ω_min)/ ω_ср,

где ω_max, ω_min , ω_ср – соответственно максимальное, минимальное и среднее значения угловой скорости начального звена за цикл.