51 Переход от неравенств к озлп.

52. Идея симплекс метода. Стандартная таблица.

Симплекс-метод решения задачи линейного программирования

Симплекс-метод представляет собой организацию процедуры поиска решения путем перемещения от опорной вершины, принадлежащей ОДР, к соседствующей с ней вершиной в сторону оптимальной вершины путем одношаговых замен одной из свободных переменных на одну из базовых вплоть до выполнения критерия эффективности.

Само слово «симплекс» определяется как многогранник, выпуклая оболочка аффинно независимых точек n-мерного пространства [16]. Давая геометрическую интерпретацию решения задачи ЛП, Дж. Б. Данциг обнаружил, что множество допустимых решений – многогранник. Название «симплекс-метод» указывает на связь, подмеченную Данцигом, теории многогранников с решением задачи линейного программирования.

Симплексный метод

Исходная задача Двойственная задача

L = х₁+2х₂+3х₃®min `L = 4у₁+6у₂®max

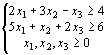
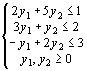
Решим обе задачи табличным симплексным методом

L – х₁-2х₂-3х₃=0 `L – 4у₁-6у₂ = 0

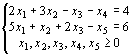
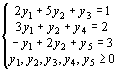
d	х1	х2	х3	х4	х5	св.		d	у1	у2	у3	у4	у5	св.
	2	3	-1	-1	0	4		у3	2	5	1	0	0	1
	5	1	2	0	-1	6		у4	3	1	0	1	0	2
L	-1	-2	-3	0	0	0		у5	-1	2	0	0	1	3
								`L	-4	-6	0	0	0	0

 

d		х1			х2			х3			х4			х5			св.						d			у1			у2			у3			у4			у5			св.
			0									1												у1			1									0			0
х1		1									0												у4			0									1			0
L		0									0												у5			0									0			1
																							`L			1			4			2			0			0			2

 

d	х1	х2	х3	х4	х5	св.	`Lmax=2
х5	0				1	4	Уmax( ;0;0; ; )
х1	1				0	2	Lmin=2
L	0				0	2	`Xmin(2;0;0;0;4)