
- •5, Сочетания.
- •Тут билет № 14 №15"Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей"
- •Аксиомы стереометрии и их следствия
- •Некоторые следствия из аксиом
- •Параллельные прямые в пространстве
- •Взаимное расположение прямых в пространстве
- •Билет № 16Перпендикулярность прямой и плоскости
- •Билет № 18 Призма
- •Билет № 21 Цилиндр
- •Билет № 22 Конус
- •Билет№ 23 Пирамида
- •Билет № 24 Сложение векторов. Умножение вектора на число. Скалярное произведение векторов.
Билет № 18 Призма
Призма (от др.-греч. πρίσμα (лат. prisma) «нечто отпиленное») — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы.
Объем призмы |
|
Объем призмы ранен V = Sоснов • H. где Sоснов — площадь основания призмы. H — ее высота. Исходим из известного факта: объем параллелепипеда, равен Vпар = Sоснов • H (Sоснов - площадь основания, H — высота).
Начнем с частного случая. Пусть нам дана треугольная призма. Достроим ее до параллелепипеда. Следовательно, параллелепипед состоит из двух равных призм, поэтому
С другой стороны,
а высота призмы и параллелепипеда общая. Из равенства
следует, что
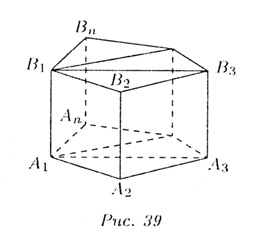
Переходим теперь к общему случаю. Дана произвольная призма. В ее основании лежит многоугольник. Проведя в нем диагонали, исходящие, из одной вершины, разбиваем многоугольник на треугольники (рис. 39). Сечения, проведенные через эти диагонали и соответствующие боковые ребра призмы делят ее на определенное число n треугольных призм. Для призмы с номером k объем равен Vk = Sk • H где Sk — площадь ее основания, H — высота первоначальной призмы. Складывая объем треугольных призм, получаем объем первоначальной призмы:
Формула установлена.
Свойства призмы
Виды призм Боковые грани правильной призмы являются равными прямоугольниками. Боковые ребра правильной призмы равны. Правильная призма является прямой. Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.
Билет № 19 Параллелепипед
Параллелепипед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.
ипы параллелепипеда Различается несколько типов параллелепипедов:
Основные элементы Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями. Свойства
Основные формулы Прямой параллелепипед Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания Прямоугольный параллелепипед Объём V=Sо*h Прямоугольный параллелепипед - это объёмная фигура, у которой шесть граней, и каждая из них является прямоугольником. Прямоугольный параллелепипед — параллелепипед, все грани которого являются прямоугольниками.
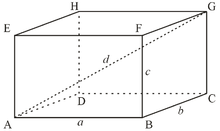
Площадь боковой поверхности Sб=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда Площадь полной поверхности Sп=2(ab+bc+ac) Объём V=abc, где a, b, c — измерения прямоугольного параллелепипеда. Билет № 20 Шар
|
|
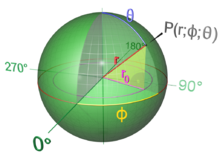
Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой. Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие плоские сечения шара называются малыми кругами. Площадь этих сечений вычисляется по формуле πR². Основные геометрические формулы Площадь
поверхности
Доказательство [скрыть]
Возьмём
четверть круга радиуса R с центром в
точке
Функция
Откуда
Доказательство [скрыть]
Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии. Определения Пусть
дано метрическое
пространство
Замечания Шар радиуса с центром также называют -окрестностью точки . Свойства
Примеры
— открытый и замкнутый отрезок соответственно.
— открытый и замкнутый диск соответственно.
— открытый и замкнутый стереометрический шар соответственно.
Тогда
Вариации и обобщения Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии. Определения Пусть дано метрическое пространство . Тогда
Замечания Шар радиуса с центром также называют -окрестностью точки . Свойства
|
|
|
|
|

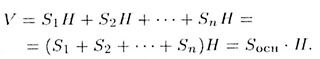
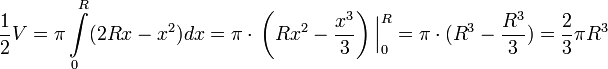
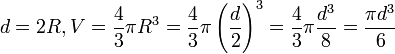 Ч.
т. д.
Ч.
т. д.