Билет № 1. Числовые последовательности и способы их задания. Конечные и бесконечные последовательности.

Рассмотрим следующие три совокупности чисел:

Естественно считать, что каждое число в любой из этих совокупностей снабжено номером в соответствии с тем местом, которое оно занимает в этой совокупности. Например, во второй совокупности число 1 имеет номер 1, число —1/2 номер 2, число 1/3 номер 3 и т. д.

Наоборот, какой бы номер мы ни указали, в каждой из этих совокупностей найдется число, снабженное этим номером. Например, номер 2 в первой последовательности имеет число 2, во второй — число —1/2, в третьей — число sin 2. Аналогично номер 10 имеют: в первой последовательности — число 10, во второй — число —1/10, в третьей — число sin 10 и т. д. Таким образом, в приведенных выше совокупностях каждое число имеет вполне определенный номер и полностью определяется этим номером.

Совокупность чисел, каждое из которых снабжено своим номером п (п = 1, 2, 3, ...), называется числовой последовательностью.

Отдельные числа последовательности называются ее членами и обозначаются обычно так: первый член a1, второй a2, .... п-й член an и т. д. Вся числовая последовательность обозначается

a1, a2, a3, ... , an, ... или {an}.

Задать числовую последовательность — это знанит указать, как отыскивается тот или иной ее член, если известен номер занимаемого им места. Существует много различных способов задания числовых последовательностей. Ниже мы остановимся на некоторых из них.

1. Обычно числовая последовательность задается с помощью формулы, позволяющей по номеру члена последовательности определить этот член. Например, если известно, что при любом п

an = n2 ,то

a1 = 1, a2 = 4, a3 = 9

и т. д. При an = sin π/2 п мы получим: a1 = sin π/2 = 1, a2 = sin π = 0, a3= sin 3π/2 = — 1, a4 = sin 2π = 0 и т. д.

Формула, позволяющая найти любой член числовой последовательности по его номеру, называется формулой общего члена числовой последовательности.

2. Бывают случаи, когда последовательность задается посредством описания ее членов. Например, говорят, что последовательность

1,4; 1,41; 1,414; 1,4142; ...

составлена из приближенных значений √2 с недостатком с точностью до 0,1; 0,01; 0,001; 0,0001 и т. д. В подобных случаях иногда вообще нельзя установить формулу общего члена; тем не менее последовательность оказывается полностью определенной.

3. Иногда указывается несколько первых членов последовательности, а все остальные члены определяются этими заданными членами по тому или иному правилу. Пусть, например, a1 = 1, a2 = 1, а каждый последующий член определяется как сумма двух предыдущих. Другими словами, при любом п > 3

an = an — 1 + an — 2

Так определяется числовая последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, .... члены которой носят название «чисел Фибоначчи» [по имени итальянского математика Леонарда Пизанского (около 1170—1250), которого называли также Фибоначчи, что означает «сын Боначчо»].Они обладают многими интересными свойствами, рассмотрение которых, однако, выходит за пределы нашей программы.

Последовательность может содержать как конечное, так и бесконечное число членов.

Последовательность, состоящая из конечного числа членов, называется конечной, а последовательность, состоящая из бесконечного числа членов, — бесконечной последовательностью.

Например, последовательность всех четных положительных чисел 2, 4, 6, 8, 10, 12, ... бесконечна, а последовательность однозначных четных положительных чисел 2, 4, 6, 8 конечна.

Билет №2 Понятие предела последовательности

Пусть каждому натуральному числу по некоторому закону поставлено в соответствие действительное или комплексное число .Тогда говорят, что этим определена последовательность чисел или, короче, последовательность.

Говорят еще, что переменная пробегает значения последовательности .

Отдельные числа последовательности называются ее элементами. Надо иметь в ввиду, что и при считаются отличными как элементы последовательности, хотя не исключено, что как числа они равны между собой, т. е. может быть .

Примеры последовательностей:

П р и м е р 1.  .

П р и м е р 2.  .

П р и м е р 3.  .

П р и м е р 4.  .

П р и м е р 5.   .

П р и м е р 6.   .

В примере 2 переменная для четных принимает одно и то же значение:

Тем не менее, мы считаем, что элементы различны.

Если все элементы последовательности равны одному и тому же числу , то ее называют постоянной.

Легко видеть, что последовательности в примерах 1, 2 и 4 ограничены. В этом случае говорят также, что соответствующие переменные, пробегающие эти последовательности, ограничены. Что касается последовательностей в примерах 3, 5 и 6, то они неограниченны. Однако последовательность в примере 3, очевидно, ограничена снизу числом 2. Что касается последовательности в примере 6, то она не ограничена как снизу, так и сверху.

Введем понятие предела последовательности.

О п р е д е л е н и е 1. Число называется пределом последовательности , если для всякого найдется (зависящее от ) число такое, что выполняется неравенствоО п р е д е л е н и е 1. Число  называется пределом последовательности , если для всякого  найдется (зависящее от ) число  такое, что выполняется неравенство

                                      (1)

для всех (натуральных) .

В этом случае пишут

 или

и говорят, что переменная    или последовательность  имеет предел, равный числу   , или стремится к . Говорят также, что переменная  или последовательность сходится к числу .

Если , то, очевидно,   .

З а м е ч а н и е. Если , то ; и обратно. Это следует из того факта, что если

,

то

,

и обратно.

Переменная примера 1 имеет предел, равный 0:

     .                                            (2)

В самом деле, зададим произвольное  и решим неравенство:

 или . 

Этим для всякого  найдено число  такое, что неравенство

выполняется для всех , и мы доказали равенство (2).

П р и м е р 7.  Переменная примера 4 стремится к 1:

.                                              (3)

В самом деле, составим неравенство

.

Оно, как мы видели, выполняется для любого , если . Это доказывает равенство (3).

П р и м е р 8.  Если , то

.                                            (4)

В самом деле, пусть пока . Неравенство

верно, если

,

т. е. если

.

Мы доказали (4) при . Если , то равенство (4) тривиально. Ведь в этом случае переменная    есть постоянная, равная нулю:

.

П р и м е р  9. Разложим положительное число  в бесконечную десятичную дробь:

.

Для его  - й срезки

имеет место равенство

.                                      (5)

В самом деле,

.

Но если задать , то всегда найдется такое , что

,

(см. предыдущий пример, где надо считать ). Поэтому

,

и мы доказали (5).

З а м е ч а н и е. Срезки  - рациональные числа. Из (5) следует, что всякое действительное число является пределом последовательности рациональных чисел.

Таким образом, всякое иррациональное число можно приблизить рациональным числом с любой наперед заданной степенью точности.

В силу этого свойства про множество  рациональных чисел говорят, что оно всюду плотно в множестве  всех действительных чисел.

Неравенство

эквивалентно двум неравенствам

 или ,

что эквивалентно тому факту, что точка    принадлежит к - окрестности точки   :

  (см. § 1.10).

Тогда определение предела можно выразить следующими словами: Число (точка)  есть предел переменной   , если, каково бы ни было , найдется такое число , что все точки    с индексами    попадут в   - окрестность точки :

.

Очевидно, какова бы ни была окрестность  точки   , найдется такое ,  что интервал  содержится в , т. е.    (рис. 7).

Поэтому тот факт, что  можно выразить еще и так: какова бы ни была окрестность    точки   , все точки , начиная с некоторого номера , должны попасть в эту окрестность, т. е. должно существовать такое число , что . Что же касается точек  с индексами , то они могут принадлежать и могут не принадлежать к . Таким образом, если вне  имеются точки , то их конечное число.

Рис. 7                                                 Рис. 8

С другой стороны, если известно, что вне  имеется только конечное число точек ,  то, обозначив

,

т. е. максимум среди индексов , мы можем сказать, что точки    с индексом    попадут в интервал . Поэтому понятие предела можно сформулировать и так: переменная  имеет своим пределом точку , если вне любой окрестности этой точки имеется конечное или пустое множество точек .

П р и м е р 10. Переменная

                               (6)

ни к какому пределу не стремится.

В самом деле, допустим, что эта переменная имеет предел, равный числу . Рассмотрим окрестность этой точки

.

Длина ее равна . Очевидно, что эта окрестность не может содержать в себе одновременно и точку 1 и точку -1 , потому что расстояние между этими точками равно . Для определенности будем считать, что точка 1 не принадлежит к нашей окрестности. Но  для , т. е. вне нашей окрестности имеется бесконечное число элементов последовательности.

Таким образом, точка  не может быть пределом нашей последовательности, и так как эта точка произвольна, то последовательность (6) не имеет предела.

Т е о р е м а 1. Если переменная  имеет предел, то он единственный.

В самом деле, допустим, вопреки теореме, что    имеет два различных предела  и   . Покроем точки  соответственно интервалами ,   настолько малой длины, чтобы эти интервалы не пересекались (рис. 8). Так как , то в интервале  находятся все элементы   , за исключением конечного их числа, но тогда интервал  не может содержать в себе бесконечное число элементов  и    не может стремиться к . Мы пришли к противоречию. Теорема доказана.

Т е о р е м а 2. Если последовательность сходится (имеет предел), то она ограничена.

Д о к а з а т е л ь с т в о. Пусть . Зададим  и подберем натуральное  так, чтобы

,

но тогда    и выполняется неравенство

для всех . Пусть    - наибольшее среди чисел

.

Тогда, очевидно,

.

Теорема доказана.

З а м е ч а н и е. Ограниченность последовательности является необходимым условием сходимости последовательности, но не достаточным, как показывает пример 10.

Т е о р е м а  3. Если переменная  имеет не равный нулю предел , то найдется такое , что

  для  .

Больше того, для указанных , если , то , если же , то . Таким образом, начиная с некоторого номера,  сохраняет знак .

Д о к а з а т е л ь с т в о. Пусть   . Тогда для  должно найтись число  такое, что

,

откуда , и первое утверждение теоремы доказано. С другой стороны, неравенство  эквивалентно следующим двум:

.

Тогда, если , то

,

а если , то

,

и этим второе утверждение теоремы доказано.

Т е о р е м а 4. Если ,  и  для всех , то .

Д о к а з а т е л ь с т в о. Допустим, что . Зададим  и подберем числа   и  так, чтобы : это возможно, потому что , а  .

Если   , то, очевидно, , и мы пришли к противоречию, так как по условию  для всех .

С л е д с т в и е.  Если элементы сходящейся последовательности  принадлежат , то ее предел также принадлежит .

Д о к а з а т е л ь с т в о. В самом деле, . Если , то по теореме 4 , что и требовалось доказать.

З а м е ч а н и е. Для интервала  для конечных  и  можно утверждать только, что если , то . Таким образом, неравенства в пределе сохраняются или обращаются в равенство. Например, , но .

Т е о р е м а 5. Если переменные и  стремятся к одному и тому же пределу  и , то переменная  также стремится к .

Д о к а з а т е л ь с т в о. Задав    можно найти    и , такие, что

,

откуда для

и

что и требовалось доказать.

Т е о р е м а 6. Если , то .

Доказательство следует из неравенства .

Билет №3 понятие о производной функции геометрический и физический смысл

Определение: Производной функции f(x) (f'(x₀)) в точке x₀  называется число, к которому стремится разностное отношение , стремящемся к нулю.

Производные элементарных функций.

Правила дифференцирования.

Если у функций  f(x) и  g(x) существуют производные, то

Производная сложной функции:

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции  y=f(x) в этой точке

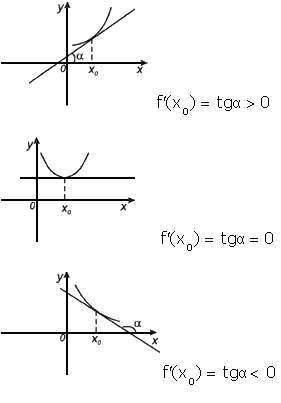
Уравнение касательной к графику функции y=f(x) в точке x₀ :

Физический смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону  x(t), то мгновенная скорость точки:

Билет №4 УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ В § 32 говорилось о том, что если точка М (а; f(а)) принадлежит графику функции у = f(х) и если в этой точке к графику функции можно провести касательную, не перпендикулярную к оси абсцисс, то угловой коэффициент касательной равен f'(а). Мы этим уже несколько раз пользовались. Например, в § 33 было установлено, что график функции у = sin х(синусоида) в начале координат образует с осью абсцисс угол 45° (точнее, касательная к графику в начале координат составляет с положительным направлением оси х угол 45°), а в примере 5 § 33 были найдены точки на графике заданной функции, в которых касательная параллельна оси абсцисс. В примере 2 § 33 было составлено уравнение касательной к графику функции у = х² в точке х = 1 (точнее, в точке (1; 1), но чаще указывают только значение абсциссы, полагая, что если значение абсциссы известно, то значение ординаты можно найти из уравнения у = f(х)). В этом параграфе мы выработаем алгоритм составления уравнения касательной.к графику любой функции. Пусть даны функция у = f(х) и точка М (а; f(а)), а также известно, что существует f'(а). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид у = кх+m, поэтому задача состоит в отыскании значений коэффициентов к и m. С угловым коэффициентом к проблем нет: мы знаем, что к = f'(а). Для вычисления значения т воспользуемся тем, что искомая прямая проходит через точку М(а; f (а)). Это значит, что, если подставить координаты точки М в уравнение прямой, получим верное равенство: f(а) = ка+m, откуда находим, что m = f(а) - ка. Осталось подставить найденные значения коэффициентов кит в уравнение прямой:

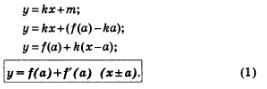Нами получено уравнение касательной к графику функции у = f(х) в точке х=а. Если, скажем, Подставив в уравнение (1) найденные значения а = 1, f(а) = 1 f'(а) = 2, получим: у = 1+2(х-f), т.е. у = 2х-1. Сравните этот результат с тем, что был получен в примере 2 из § 33. Естественно, получилось то же самое. Составим уравнение касательной к графику функции у = tg х в начале координат. Имеем: значит, соs х f'(0) = 1. Подставив в уравнение (1) найденные значения а= 0, f(а)= 0, f'(а) = 1, получим: у=х. Именно поэтому мы и провели тангенсоиду в § 15 (см. рис. 62) через начало координат под углом 45° к оси абсцисс. Решая эти достаточно простые примеры, мы фактически пользовались определенным алгоритмом, который заложен в формуле (1). Сделаем этот алгоритм явным. АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ  К ГРАФИКУ ФУНКЦИИ у = f(x) 1)    Обозначить абсциссу точки касания буквой а. 2)    Вычислить 1 (а). 3)    Найти f'(х) и вычислить f'(а). 4)    Подставить найденные числа а, f(а), (а) в формулу (1).

Пример 1. Составить уравнение касательной к графику функции в точке х = 1. Решение. Воспользуемся алгоритмом, учитывая, что в данном примере

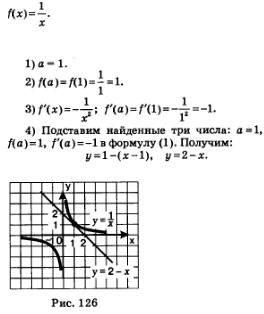
На рис. 126 изображена гипербола , построена прямая у= 2-х. Чертеж подтверждает приведенные выкладки: действительно, прямая у = 2-х касается гиперболы в точке(1; 1).

Ответ: у =2- х. Пример 2. К графику функции провести касательную так, чтобы она была параллельна прямой у =4х - 5. Решение. Уточним формулировку задачи. Требование «провести касательную» обычно означает «составить уравнение касательной». Это логично, ибо если человек смог составить уравнение касательной, то вряд ли он будет испытывать затруднения с построением на координатной плоскости прямой по ее уравнению. Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Но в отличие от предыдущего примера здесь имеется неясность: не указана явно абсцисса точки касания. Начнем рассуждать так. Искомая касательная должна быть параллельна прямой у = 4х-5. Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты. Значит, угловой коэффициент касательной должен быть равен угловому коэффициенту заданной прямой:   Таким образом, значение а мы можем найти из уравнения f'(а)= 4. Имеем: Из уравнения Значит, имеются две касательные, удовлетворяющие условию задачи: одна в точке с абсциссой 2, другая в точке с абсциссой -2. Теперь можно действовать по алгоритму.

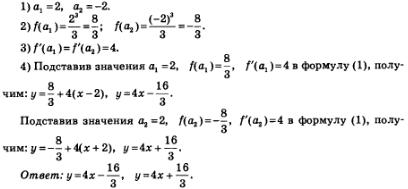Пример 3. Из точки (0; 1) провести касательную к графику функции Решение. Воспользуемся алгоритмом составления уравнения касательной, учитывая, что в данном примере Заметим, что и здесь, как в примере 2, не указана явно абсцисса точки касания. Тем не менее действуем по алгоритму.

По условию касательная проходит через точку (0; 1). Подставив в уравнение (2) значения х = 0, у = 1, получим: Как видите, в этом примере только на четвертом шаге алгоритма нам удалось найти абсциссу точки касания. Подставив значение а =4 в уравнение (2), получим:

На рис. 127 представлена геометрическая иллюстрация рассмотренного примера: построен график функции

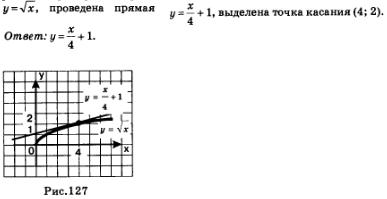
В § 32 мы отметили, что для функции у = f(х), имеющей производную в фиксированной точке х, справедливо приближенное равенство:

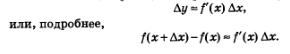Для удобства дальнейших рассуждений изменим обозначения: вместо х будем писать а, вместо будем писать х и соответственно вместо будем писать х-а. Тогда написанное выше приближенное равенство примет вид:

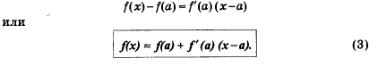А теперь взгляните на рис. 128. К графику функции у = f(х) проведена касательная в точке М (а; f (а)). Отмечена точка х на оси абсцисс близко от а. Ясно, что f(х) — ордината графика функции в указанной точке х. А что такое f(а) + f'(а) (х-а)? Это ордината касательной, соответствующая той же точке х — см. формулу (1). В чем же смысл приближенного равенства (3)? В том, что для вычисления приближенного значения функции берут значение ординаты касательной.

Пример 4. Найти приближенное значение числового выражения 1,02⁷. Решение. Речь идет об отыскании значения функции у = х⁷ в точке х = 1,02. Воспользуемся формулой (3), учтя, что в данном примере В итоге получаем: Если мы воспользуемся калькулятором, то получим: 1,02⁷ = 1,148685667... Как видите, точность приближения вполне приемлема. Ответ: 1,02⁷ =1,14.

Билет №5 Производные основных элементарных функций

Производная степенной функции.

y=xμ,μ∈R. 

y/=limΔx→0ΔxΔy=limΔx→0Δx(x+Δx)μ−xμ=limΔx→0Δxxμ[(xx+Δx)−1]=limΔx→0xΔx·xxμ[(1+xΔx)−1]= =limΔx→0xΔxxμ−1[(1+xΔx)−1]=[xΔx=t,Δx→0,t→0]=limt→0xμt(1+t)μ−1=xμ·μ, 

[xμ]/=μ·xμ−1.

 Производная логарифмической функции.

y=logax,

 y/=limΔx→0ΔxΔy=limΔx→0Δxloga(x+Δx)−logax=limΔx→0Δxloga(xx+Δx)=limΔx→0xxΔxloga(1+xΔx)= =limΔx→0x1·loga(1+xΔx)·1xΔx=[t=xΔx,Δx→0,t→0]=limt→0x1·t1·loga(1+t)=x1limt→0loga(1+t)t1= =x1loga[limt→0(1+t)t1]=x1logae=1xlna, 

[logax]/=1xlna.

 Производная показательной функции.

y=ax,

y/=limΔx→0ΔxΔy=limΔx→0Δxax+Δx−ax=limΔx→0Δxax(aΔx−1)=axlna,

[ax]/=axlna.

 Производные тригонометрических функций.

y=sinx,

y/=limΔx→0Δxsin(x+Δx)−sinx=limΔx→0Δx2sin2Δxcos22x+Δx=limΔx→0Δx22Δxcos(x+2Δx)=cosx,(sinx)/=cosx.

(cosx)/=−sinx. 

y=tgx,

y/=cos2x(sinx)/cosx−(cosx)/sinx=cos2xcos2x+sin2x=1cos2x,

(tgx)/=1cos2x.

(ctgx)/=−1sin2x.

Производные обратных тригонометрических функций.

y=arcsinx.

Применим теорему о нахождении производной обратной функции:

x=siny,

y/(x)=1x/(y)=1cosy=1√1−sin2y=1√1−[sinarcsinx]2=1√1−x2. 

y=arccosx,

x=cosy,

y/(x)=1x/(y)=1−siny=−1√1−cos2y=−1√1−[cos(arccosx)]2=−1√1−x2. 

y=arctgx,

x=tgy,

y/(x)=1x/(y)=cos2y=cos2ycos2y+sin2y=11+tg2y=11+[tg(arctgx)]2=11+x2.

y=arcctgx,

x=ctgy,

y/(x)=1x/(y)=−sin2y=−sin2ysin2y+cos2y=−11+ctg2y=−11+[ctg(arcctgx)]2=−11+x2.

Билет №6 "Применение производной к исследованию функций".

Достаточное условие возрастания функции

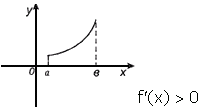
Если в каждой точке интервала (a, b) f'(x)>0, то функция  f(x) возрастает на этом интервале.

Достаточное условие убывания функции.

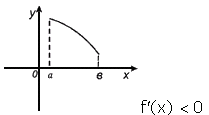
Если в каждой точке интервала (a, b) f'(x)<0, то функция  f(x) убывает на этом интервале.

Определение:

x₀ называется критической точкой функции  f(x), если

1) x₀ – внутренняя точка области определения  f(x) ;

2) f'(x₀)=0 или f'(x₀) не существует.

Необходимое условие экстремума:

Если x₀– точка экстремума функции  f(x), то эта точка является критической точкой данной функции.

Достаточное условие экстремума:

Если при переходе через точку x₀ производная функции меняет знак, то x₀ – точка экстремума функции  f(x).

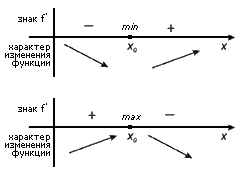
Примеры экстремумов:

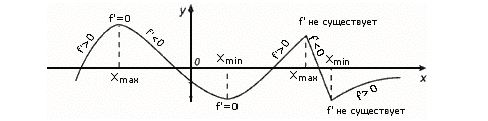
Схема исследования функции.

1. Найти область определения функции.

2. Проверить, не является ли функция четной или нечетной; проверить также, не является ли она периодической.

3. Найти, если это возможно, точки пересечения графика функции с осями координат и промежутки знакопостоянства функции. Иногда для уточнения построения графика следует найти две три дополнительные точки.

4. Найти производную функции и ее критические точки.

5. Найти промежутки монотонности и экстремумы функции.

6. Построить график функции, используя полученные результаты исследования.

Схема нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке [a; b].

1. Найти значения функции в концах отрезка, т.е. f(a) и f(b) ;

2. Найти значения функции в тех критических точках, которые принадлежат интервалу (a,b) ;

3.  Из найденных значений выбрать наибольшее и наименьшее.

Билет№ 8 Первообразная и неопределенный интеграл

Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).

Обозначение

где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.

П.2. Свойства неопределенного интеграла

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

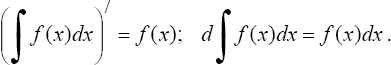
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

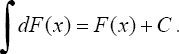
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

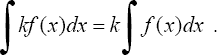
4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

Билет№9 Нахождение площади криволинейной трапеции 1. Нахождение площади криволинейной трапеции

Криволинейной трапецией называется фигура, расположенная в прямоугольной системе координат и ограниченная осью абсцисс, прямыми х = а и х = b и кривой , причем неотрицательна на отрезке . Приближенно площадь криволинейной трапеции можно найти так:

разделить отрезок оси абсцисс на n равных отрезков;

провести через точки деления отрезки, перпендикулярные к оси абсцисс, до пересечения с кривой ;

заменить получившиеся столбики прямоугольниками с основанием и высотой, равной значению функции f в левом конце каждого отрезка;

найти сумму площадей этих прямоугольников.

Но можно найти площадь криволинейной иначе: по формуле Ньютона-Лейбница. Для доказательства формулы, носящей их имена, докажем, что площадь криволинейной трапеции равна , где – любая из первообразных функции , график которой ограничивает криволинейную трапецию.

Вычисление площади криволинейной трапеции записывается так:

находится любая из первообразных функции .

записывается . - это формула Ньютона-Лейбница.

Билет №10 формула Ньютона-Лейбница.

Чтобы решить определенный интеграл, надо сначала вычислить неопределенный интеграл (или найти первообразную), а затем вычислить определенный интеграл, подставив первообразную подынтегральной функции в формулу Ньютона-Лейбница:

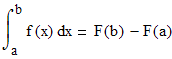
Здесь F(x) - первообразная для функции f(x)! Таким образом, чтобы применить формулу Ньютона-Лейбница, надо вычислить значение первообразной при верхнем пределе интегрирования B, при нижнем пределе интегрирования - A, а затем взять их разность F(b)-F(a). Вначале мы рассмотрим доказательство данной формулы, а затем приведем Примеры решения интегралов по основной формуле интегрального и дифференциального исчисления.

Доказательство формулы Ньютона-Лейбница

Чтобы доказать данную теорему введем вспомогательную функцию

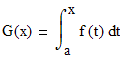
Здесь мы поступили следующим образом Мы заменили верхний предел интегрирования на переменную x; Вместо х под знаком интеграла написали переменную t. Это возможно поскольку значение определенного интеграла не зависит от обозначения переменной интегрирования:

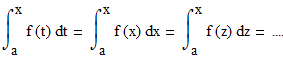
Функция G(x) представляет собой Интеграл с переменным верхним пределом интегрирования! Теперь к этой функции мы применим определение производной как предел разностного отношения.

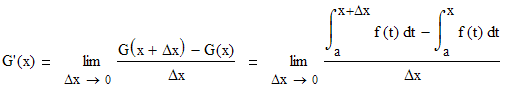
Преобразуем числитель данной формулы, используя Свойства определенного интеграла

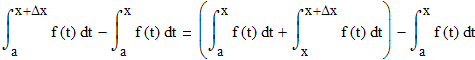
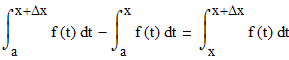
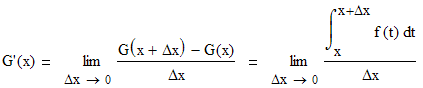
Теперь нам понадобится Теорема о среднем значении для определенного интеграла

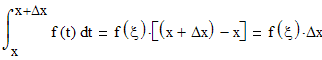
Здесь точка лежит между x и поэтому, когда стремится к нулю, стремится к х!

Это означает, что интеграл с переменным верхним пределом является первообразной для функции f(x). Любая другая первообразная подынтегральной функции отличается от данной первообразной на постоянную:

отсюда

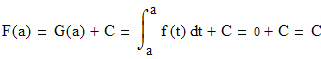
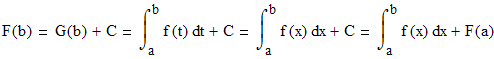
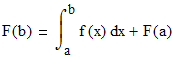
И формула Ньютона-Лейбница доказана

Примеры решения интегралов по Формуле Ньютона-Лейбница

Пример 1

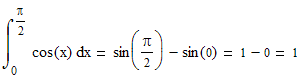
Пример 2

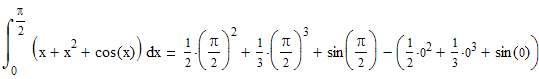
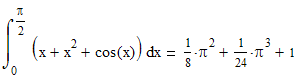
Пример 3

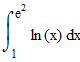
Сначала найдем неопределенный интеграл, применив формулу интегрирования по частям:

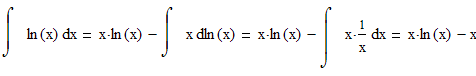
Теперь подставляем первообразную в формулу Ньютона-Лейбница:

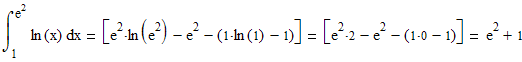
Интересный результат получился! Интеграл равен сумме своих пределов интегрирования: Если

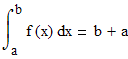
Билет№ 11Основные понятия комбинаторики

Определение : Размещением из п элементов по т называется любое упорядоченное подмножество из т элементов множества, состоящего из п элементов.

На практике чаще представляет интерес не конкретный вид размещений, а их количество. Следующая теорема дает общую формулу для вычисления размещений.

  Теорема: Число размещений из n элементов по m равно 

  Доказательство: необходимо заполнить т мест элементами множества из п элементов. Каждое действие- это выбор определенного элемента. Действия совершаются последовательно, значит применимо правило умножения. Первый элемент можно выбрать п способами, второй- (п-1) способами, последний т-ый элемент- (п-(т-1)) способами. Тогда количество размещений равно п(п-1)(п-2)…(п-(т-1)). Умножим и разделим данное выражение на (п-т)!, преобразовав получим более удобный вид :

Пример. Сколько можно составить четырехзначных чисел, состоящих из разных цифр, использую все 10 цифр?

Решение: В числе важен порядок следования цифр. Следовательно, нужно найти количество размещений из 10 по 4: 

 

Но среди них есть числа с нулем в начале. из полученного значения 5040 необходимо вычесть количество таких чисел. Найдем это количество: т.к. на первом месте стоит о, то оставшиеся три выбираем из 9, т.е. 

Искомое количество чисел равно 5040-504=4536.

                                                                                    

4.      Перестановки.

Рассмотрим случай, когда п=т. Такие размещения называются перестановками.

  Определение: Перестановкой из п элементов называется любое упорядоченное множество , в которое входят по одному разу все п различных элементов данного множества.

Формулу для определения количества перестановок дает теорема.

  Теорема: Число перестановок п различных элементов равно п!, т.е. Р_п=п!

   Доказательство: 

Следовательно, Р_n= n!

  Пример1: Сколькими способами можно расставить 4 книги на полке?

Решение: Необходимо составить всевозможные упорядоченные множества из 4 элементов, т.е. составить перестановки. Количество их равно Р₄=4!=24.

Пример2: Сколькими способами можно расставить 9 книг на полке, но чтобы определенные 4 книги стояли рядом.

Решение: Будем считать выделенные 4 книги за один элемент. Тогда данное множество содержит 6 элементов. Количество способов расстановки этих элементов есть количество перестановок из 6 элементов: Р₆=6!=720. Но сами 4 книги, которые стоят рядом можно расставить Р₄=4!=24 способами. Расстановка 4 книг- это первое действие, расстановка 5 книг с блоком из 4-х книг - это второе действие. Данные действия последовательны, значит применимо правило умножения. Тогда способов всего 720 _·24=17280.

                                                                                   

5, Сочетания.

В размещениях и перестановках важен порядок элементов. Рассмотрим случаи, когда порядок элементов в множествах не учитывается, т.е. случаи составления неупорядоченных множеств. Например:

Из чисел 3, 5, 2 составить всевозможные произведения из двух различных множителей.

Для произведения справедлив переместительный закон (свойство коммутативности), значит необходимо составить неупорядоченные подмножества из двух элементов множества, состоящего из трех элементов. Такие подмножества называются сочетаниями.

Определение: Сочетанием из п элементов по т называется любое неупорядоченное множество из т элементов, которые принадлежат множеству, состоющему из п элементов.

Вернемся к задаче. Составим требуемые произведения:

 

Как видим, в сочетаниях не учитываются перестановки элементов в каждом построенном подмножестве. Учтем это при доказательстве следующей теоремы.

Теорема: Число сочетаний из п элементов по т равно 

  Доказательство: Число размещений из п по т можно получить следующим образом: выбирать по т элементов, не учитывая порядок. Это есть сочетания из п по т. А затем в каждом подмножестве произвести перестановки. Пользуясь правилом умножения, получим

  . 

Откуда имеем:

Свойства сочетаний:

Пример 1. Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных?

Решение: Среди выбранных шаров 4 белых и 3 черных. Т.к. порядок не учитывается, то белые можно выбрать _{количеством способов, равным} 

_,

а черные

 

 По правилу умножения искомое число способов равно _{210·10=2100.}

Пример2. Сколькими способами группу из 12 человек можно разбить на две подгруппы, в одной из которых должно быть не менее 5, а в другой- не более 9 человек?

Решение: Первая подгруппа может состоять либо из трех, либо из четырех, либо из пяти человек. Соответствующие количества способов равны: 

 

Учитывая, что выбор первой подгруппы одновременно означает выи выбор второй, по правилу сложения найдем искомое число способов: ₂₂₀ +495+792=1507.

Пример 3. 10 команд участвуют в розыгрыше первенства по футболу, лучшие из которых занимают 1-е, 2-е и 3-е места. Две команды, занявшие последние места, не будут участвовать в следующем первенстве. Сколько разных вариантов результата первенства может быть, если учитывать только положение первых трех и последних двух команд?

Решение: Распределение первых трех мест - это размещения

   

В результате остается 7 команд, две из которых выбывают из следующего первенства. Порядок выбывших команд не важен, поэтому это может произойти _С72=21 способами. По правилу умножения имеем искомый результат 720 _·21=15120.

Билет № 12событие,вероятность,сложение и умножение вероятностей

Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записываем .

События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В.

Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:

.

Если случайные события образуют полную группу несовместных событий, то имеет место равенство

.

Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле

.

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:

.

Вероятность произведения зависимых событий вычисляется по формуле условной вероятности (см. следующий раздел).

Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Решение. Обозначим события: А – вынули белый шар из первого ящика, ;

- вынули черный шар из первого ящика, ;

В – белый шар из второго ящика, ;

- черный шар из второго ящика, .

Нам нужно, чтобы произошло одно из событий или . По теореме об умножении вероятностей , . Тогда искомая вероятность по теореме сложения будет .

Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.

Решение.

Пусть А – попадание первого стрелка, ;

В – попадание второго стрелка, .

Тогда - промах первого, ;

- промах второго, .

Найдем нужные вероятности.

а) АВ – двойное попадание,

б) – двойной промах, .

в) А+В – хотя бы одно попадание,

.

г) – одно попадание,

.

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

Решение.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

2. .

3.

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

Если события имеют одинаковую вероятность , то формула принимает простой вид:

.

Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события (попадание первого орудия), (попадание второго орудия) и (попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям , и (т. е. вероятности промахов), соответственно равны:

, ,

Искомая вероятность .

Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События "машина работает" и "машина не работает" (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице:

Отсюда вероятность того, что машина в данный момент не работает, равна

Искомая вероятность

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие "при n выстрелах стрелок попадает в цель хотя бы один раз". События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула .

Приняв во внимание, что, по условию, (следовательно, ), получим

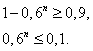
Прологарифмируем это неравенство по основанию 10:

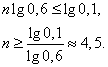
Итак, , т.е. стрелок должен произвести не менее 5 выстрелов.

Билет № 13Взаимное расположение двух прямых в пространстве  

Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.

1. Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые.

2. Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются.

3. В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны).

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются.

На рис. 26 прямая a лежит в плоскости , а прямая с пересекает в точке N. Прямые a и с — скрещивающиеся.

Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.

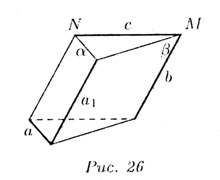
На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость || b (в плоскости указана прямая a₁ || b).

Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты.