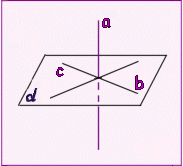
Взаимное расположение прямых в пространстве

Пересекающиеся прямые: лежат в одной плоскости, имеют одну общую точку.	Параллельные прямые: лежат в одной плоскости, не имеют общих точек (не пересекаются)	Скрещивающиеся прямые: не лежат в одной плоскости, не имеют общих точек (не пересекаются)

Параллельность плоскостей Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют ни одной общей точки. α∥β.

Признак параллельности двух плоскостей Теорема. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости , то эти плоскости параллельны. Если а∥а1 и b∥b1, то α∥β.

Свойства параллельных плоскостей

Вели α∥β и они пересекаются с γ, то а∥b. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

Если α∥β и AB∥CD, то АВ = CD. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны .

Билет № 16Перпендикулярность прямой и плоскости

Определение Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения. Смотри также опорную задачу №1.

Теорема 1 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости. Доказательство.

Теорема 2 1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой. Доказательство.

Теорема 3 2-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Две прямые, перпендикулярные одной и той же плоскости, параллельны.

Теорема 2 1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

Доказательство: Пусть а₁ и а₂ - 2 параллельные прямые и плоскость, перпендикулярная прямой а₁. Докажем, что эта плоскость перпендикулярна и прямой а₂. Проведем через точку А₂ пересечения прямой а₂ с плоскостью произвольную прямую х₂ в плоскости . Проведем в плоскости через точку А₁ пересечения прямой а₁ с прямую х₁, параллельную прямой х₂. Так как прямая а₁ перпендикулярна плоскости , то прямые а₁ и x₁перпендикулярны. А по теореме 1 параллельные им пересекающиеся прямые а₂ и х₂ тоже перпендикулярны. Таким образом, прямая а₂ перпендикулярна любой прямой х₂ в плоскости . А это ( по определению )значит, что прямая а₂ перпендикулярна плоскости . Теорема доказана.

Теорема 3 2-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Две прямые, перпендикулярные одной и той же плоскости, параллельны.

Доказательство: Пусть а и b - 2 прямые, перпендикулярные плоскости . Допутим, что прямые а и b не параллельны. Выберем на прямой b точку С, не лежащую в плоскости . Проведем через точку С прямую b₁, параллельную прямой а. Прямая b₁ перпендикулярна плоскости по теореме 2. Пусть В и В₁ - точки пересечения прямых b и b₁ с плоскостью . Тогда прямая ВВ₁ перпендикулярна пересекающимся прямым b и b₁. А это невозможно. Мы пришли к противоречию. Теорема доказана.

Билет № 17

Определение Две пересекающиеся плоскости, называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Теорема 5 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Доказательство.

Теорема 5 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство: Пусть - плоскость , b - перпендикулярная ей прямая, - плоскость проходящая через прямую b, и с - прямая по которой пересекаются плоскости и . Докажем, что плоскости и перпендикулярны. Проведем в плоскости через точку пересечения прямой b с плоскостью прямую а, перпендикулярную прямой с. Проведем через прямые а и b плоскость . Она перпендикулярна прямой с, так как прямые а и b перпендикулярны, то плоскости и перпендикулярны. Теорема доказана.