Билет №10
Вынужденные колебания при наличии трения.
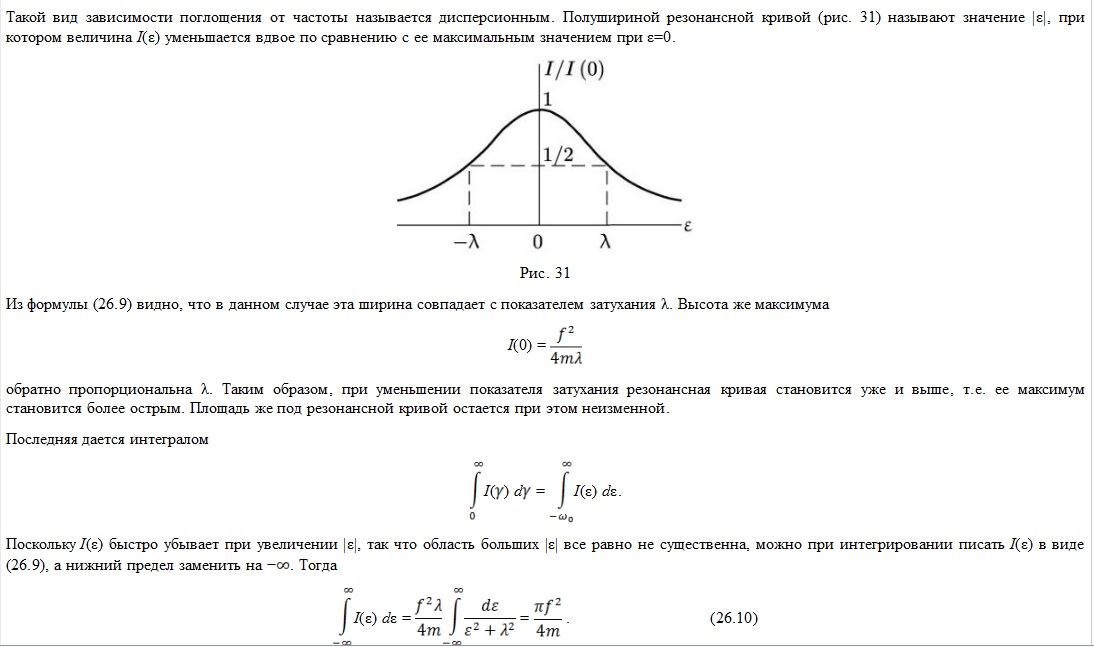
В
ынужденные
колебания при наличии трения.
Билет №11
Колебания математического маятника с быстро колеблющейся точкой подвеса. Эффект Капицы.
Ма́ятником Капицы называется система, состоящая из грузика, прикрепленного к легкой нерастяжимой спице, которая крепится к вибрирующему подвесу.
Обозначения
Направим
ось
вертикально вверх а
ось
горизонтально, так чтобы плоское движение
маятника происходило в плоскости (
-
)
Введем
обозначения:
— частота
вынуждающих вертикальных гармонических
колебаний подвеса,
— амплитуда
вынуждающих колебаний,
— собственная
частота колебаний математического
маятника,
— ускорение
свободного падения,
— длина
легкого стержня,
— масса грузика
Если угол между стержнем и осью обозначить как то зависимость координат грузика от времени запишется следующими формулами:
Билет №12
Колебания со многими степенями свободы.
Колебания с несколькими степенями свободы
Системами с n степенями свободы принято в динамике называть такие системы, для полной фиксации геометрического состояния которых в любой момент времени требуется задать n параметров, например положение (прогибы) n точек. Положение прочих точек определяется обычными статическими приемами.
Примером системы с n степенями свободы может служить балка или плоская рама, если массы ее отдельных частей или элементов условно (для облегчения динамического расчета) считаются сосредоточенными в n точках, или если она несет n больших масс (двигатели, моторы), по сравнению с которыми возможно пренебречь собственным весом элементов. Если отдельные сосредоточенные («точечные») массы могут при колебаниях совершать перемещения по двум направлениям, то число степеней свободы системы будет равно числу связей, которые следует наложить на систему, чтобы ликвидировать смещения всех масс.
Если вывести из равновесия систему с n степенями свободы, то она будет совершать свободные колебания, причем каждая «точка» (масса) будет совершать сложные полигармонические колебания типа:
Число собственных частот системы равно числу ее степеней свободы.
Билет №13
Колебания в цепочке из N-осцилляторов.
Билет №15
Понятие волны. Фазовая и групповая скорость волны.
Групповая скорость — это величина, характеризующая скорость распространения «группы волн» - то есть более или менее хорошо локализованной квазимонохроматической волны (волны с достаточно узким спектром). Обычно интерпретируется как скорость перемещения максимума амплитудной . В случае рассмотрения распространения волн в пространстве размерностью больше единицы подразумевается как правило волновой пакет близкий по форме к плоской волне.
Групповая скорость во многих важных случаях определяет скорость переноса энергии и информации. Групповая скорость определяется динамикой физической системы, в которой распространяется волна (конкретной среды, конкретного поля итп). В большинстве случаев подразумевается линейность этой системы (точно или приближенно).
Фа́зоваяско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения, в пространстве вдоль заданного направления. Обычно рассматривают направление, совпадающее с направлением волнового вектора, и фазовой называют скорость, измеренную именно в этом направлении, если противное не указано явно (то есть если явно не указано направление, отличное от направления волнового вектора). Фазовая скорость по направлению волнового вектора совпадает со скоростью движения фазового фронта (поверхности постоянной фазы). Ее можно рассматривать при желании как векторную величину.