Билет №8

Колебания с трением. Диссипативная функция.

Диссипативная функция

Диссипати́вная функция (функция рассеяния) — функция, вводимая для учёта перехода энергии упорядоченного движения в энергию неупорядоченного движения, в конечном счёте — в тепловую, например, для учёта влияния сил вязкого трения на движение механической системы. Диссипативная функция характеризует степень убывания механической энергии этой системы. Диссипативная функция, делённая на абсолютную температуру, определяет скорость, с которой возрастает энтропия в системе (т. н. производство энтропии). Диссипативная функция имеет размерность мощности

Применение понятия

Понятие о Диссипативной функции используется при изучении движения диссипативных систем, в частности для учёта влияния сопротивлений на малые колебания системы около её положения равновесия, для исследования затухания колебаний в упругой среде, для учёта тепловых потерь при затухании колебаний электрического тока в системе контуров и др. С учётом диссипации уравнения Лагранжа записываются в виде

где L — функция Лагранжа, и — обобщённые координаты и их частные производные по времени, F — диссипативная функция.

Билет №9

Вынужденные колебания без трения. Биения. Резонанс.

Вынужденные колебания без трения

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Уравнение вынужденных колебаний запишется в виде где 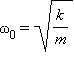– собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине величина A определяется выражением: Уравнение (**) не учитывает действия сил трения. Уравнение вынужденных колебаний (**) содержит две частоты – частоту ω0 свободных колебаний и частоту ω вынуждающей силы.

Биения

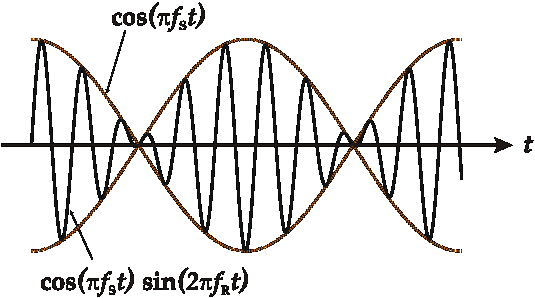
Бие́ния — явление, возникающее при наложении двух гармонических колебаний, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Биения модулируются по амплитуде. Распространение такого вида колебаний менее эффективно. Частота изменения амплитуды суммарного сигнала равна разности частот двух исходных сигналов.

Биения возникают от того, что один из двух сигналов постоянно отстаёт от другого по фазе и в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается усилен, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того как нарастает отставание.

Резонанс

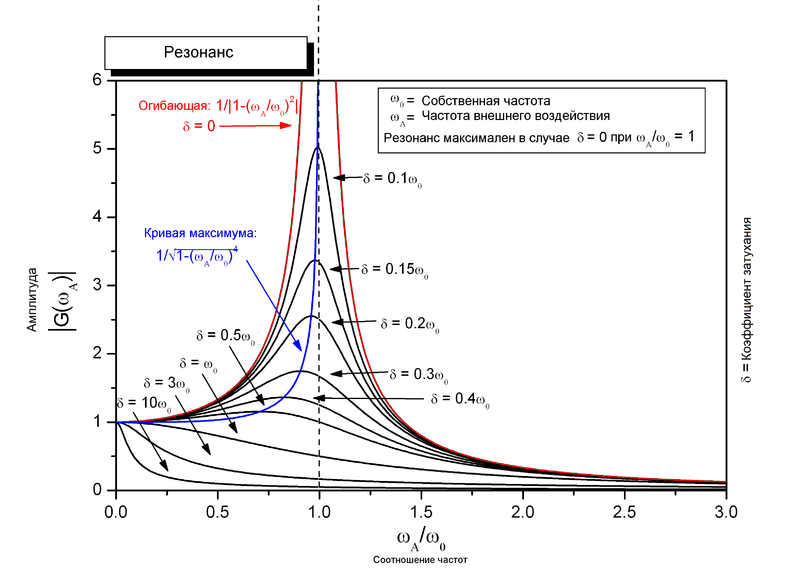
Резона́нс— явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность

Механика

Резонансная частота

где g это ускорение свободного падения, а L — длина от точки подвешивания маятника до центра его масс. Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной

Струна

Частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны .Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

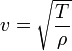
Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

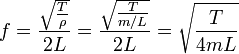
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.