Билет №6

Функция Лагранжа. Уравнения Лагранжа. Обобщенные импульсы, энергия. Цикличе-ские координаты. Функция Гамильтона и уравнения Гамильтона.

Функция Лагранжа

Функция Лагранжа- функция L(X,λ), определенная выражением L(X,λ) = F(X) + ∑λiφi(x), где λi - множители Лагранжа.

Функция Лагранжа используется при решении задач на условный экстремум.

Правило множителей Лагранжа

Если x*=(x1,..., xn) - решение задачи на условный экстремум, то существует хотя бы одна ненулевая система множителей Лагранжа λ*(λ1,...,λm) такая, что точка (x*) является точкой стационарности функции Лагранжа по переменным xj и λi, рассматриваемым, как независимые переменные.

Метод множителей Лагранжа заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — функции Лагранжа.

Уравнения Лагранжа

Уравнение Эйлера — Лагранжа

Использование уравнений Эйлера — Лагранжа для нахождения экстремума функционала в некотором смысле аналогично использованию теоремы дифференциального исчисления, утверждающей, что лишь в точке, где первая производная функции обращается в нуль, гладкая функция может иметь экстремум (в случае векторного аргумента приравнивается нулю градиент функции, то есть производная по векторному аргументу). Точнее говоря, это прямое обобщение соответствующей формулы на случай функционалов — функций бесконечномерного аргумента.

Утверждение

Пусть задан функционал 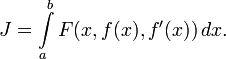с подынтегральной функцией обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом, где через f' обозначена первая производная f по x. Если этот функционал достигает экстремума на некоторой функции то для неё должно выполняться обыкновенное дифференциальное уравнение которое называется уравнением Эйлера — Лагранжа.

Уравнения Лагранжа первого рода

Уравнения Лагранжа первого рода — дифференциальные уравнения движения механической системы, записанные в декартовых координатах и содержащие множители Лагранжа.

Уравнения Лагранжа первого рода, в некоторых случаях удобно использовать для нахождения реакций связей, если закон движения уже найден каким-либо другим способом (Например с помощью Уравнений Лагранжа второго рода).

Уравнения Лагранжа второго рода

Уравнениями Лагранжа второго рода называют дифференциальные уравнения движения механической системы, получаемые при применении лагранжева формализма.

Уравнение Д’Аламбера

Уравнение Д’Аламбера — дифференциальное уравнение вида где и — функции.

Обобщенные импульсы, энергия

ОБОБЩЁННЫЕ ИМПУЛЬСЫ, физич. величины рi, определяемые ф-лами: pi=дT/дqi или pi=дL/дqi, где Т — кинетич. энергия, a L — Лагранжа функция данной механич. системы, выраженные через обобщённые координаты qi и обобщённые скорости qi. Размерность О. и. зависит от размерности обобщённой координаты. Если qi имеет размерность длины, то pi — размерность обычного импульса, т. е. произведения массы на скорость; если же координатой qi явл. угол (величина безразмерная), то pi имеет размерность момента кол-ва движения, и т. д.

Циклические координаты

ЦИКЛИЧЕСКИЕ КООРДИНАТЫ, обобщённые координаты механич. системы, не входящие явно в Лагранжа функцию или в др. характеристич. функции этой системы. Наличие Ц. к. упрощает процесс решения (интегрирования) соответствующих дифф. ур-ний движения механич. системы. Напр., если в ф-ции Лагранжа L не входит явно координата q1; то первое из ур-ний Лагранжа примет вид

(d/dt)(дL/дq1)=0 и сразу даёт интеграл

дL/дq1=const.

Функция Гамильтона и уравнения Гамильтона

Функция Гамильтона - характеристическая функция механической системы, выраженная через канонические переменные: обобщенные координаты и обобщенные импульсы Для системы со связями, явно не зависящими от времени движущейся в стационарном потенциальном силовом поле, функция Гамильтона где П - потенциальная, а Т - кинетическая энергия системы, в выражении которой произведена замена всех обобщенных скоростей на с помощью равенств Таким образом, функция Гамильтона равна в этом случае полной механической энергии системы, выраженной через и В общем случае функция Гамильтона может быть определена через функцию Лагранжа равенством в котором все должны быть выражены также через

Уравне́ния Гамильто́на — система дифференциальных уравнений:

где точкой над p и q обозначена производная по времени. Система состоит из 2N дифференциальных уравнений первого порядка (j = 1, 2, …, N) для динамической системы, описываемой N (обобщёнными) координатами, являющихся уравнениями движения (одной из форм таких уравнений, наравне с уравнениями Лагранжа, являющейся обобщением ньютоновских уравнений движения) системы, где — так называемая функция Гамильтона, также иногда именуемая гамильтонианом, — время — (обобщенные) координаты и — обобщенные импульсы определяющие состояние системы (точку фазового пространства).