Билет №5

Система двух частиц. Приведенная масса. Центральное поле. Законы Кеплера.

Приведенная масса

Приведённая масса — условная характеристика распределения масс в движущейся механической или смешанной (например, электро-механической) системе, зависящая от физических параметров системы (масс, моментов инерции, индуктивности и др.) и от её закона движения

Обычно приведенная масса определяется из равенства где -- кинетическая энергия системы, а — скорость той точки системы, к которой приводится масса. В более общем виде приведённая масса является коэффициентом инерции в выражении кинетической энергии системы со стационарными связями, положение которой определяется обобщёнными координатами

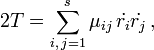где точка означает дифференцирование по времени, а есть функции обобщённых координат.

Центральное поле

Поле называется центральным, если во всех точках поля векторы напряженности направлены вдоль прямых, которые пересекаются в одной точка, неподвижной по отношению к какой-либо инерциальной системе отсчета. В частности, гравитационное поле материальной точки является центральным: во всех точках поля векторы g и F=mg, действующие на тело, внесенное в гравитационное поле, направлены радиально от массы М, создающей поле, к точечной массе m

Законы Кеплера

1 Закон!

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

Форма эллипса и степень его сходства с окружностью характеризуется отношением  , где   — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),   — большая полуось. Величина   называется эксцентриситетомэллипса. При   и   эллипс превращается в окружность

2 Закон

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца поэклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

3 Закон

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

, где   и   — периоды обращения двух планет вокруг Солнца, а   и   — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:  , где   — масса Солнца, а   и   — массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.