Задачи для самостоятельного решения

1. Решить систему линейных уравнений методом Гаусса:

2. Решить систему линейных уравнений по правилу Крамера:

3. Вычислить определитель а) по правилу Сарюса; б) путём приведения к треугольному виду; в) с помощью разложения по строке или по столбцу:

1) ; 2) .

4. Даны матрицы , , , .

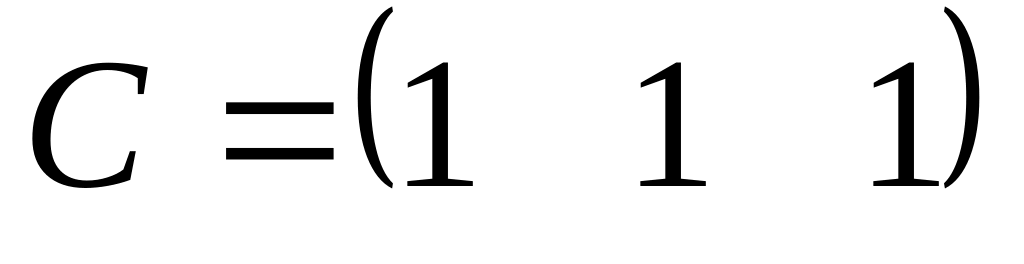Вычислить: C(AB +B )D.

5. Вычислить матрицу, обратную к :

.

Сделать проверку.

6. Установить, являются ли векторы линейно зависимыми:

(8, -3, -4), (-1, 1, 1), (4, 1, 0).

7. Установить, образуют ли векторы (2, -3, -4), (-1, 1, -1), (1, 0, 1) базис в пространстве R . Если да, то разложить вектор (3, -3, -3) по этому базису.

8. Линейный оператор , действующий в пространстве R , задан своей матрицей в некотором базисе. Координаты вектора в том же базисе: . Найти координаты вектора  ( ) в этом базисе.

9. Два линейных оператора  и , действующих в пространстве R , заданы своими матрицами в одном и том же базисе: , . Найти матрицы операторов –3,  + и  в том же базисе.

10. Найти собственные значения и собственные векторы линейного оператора, матрица которого в некотором базисе есть .

11. Даны векторы (2, -3, -4), (-1, 1, -1), (1, 0, 1). Вычислить: (точка обозначает скалярное произведение).

12. Найти угол между векторами (1, 1, 1) и (-1, 1, 1).

13. Найти координаты точки пересечения медиан треугольника АВС, если (3, -2, 2), (1, -3, 1), (2, 0, 4). Найти длины медиан этого треугольника. (Можно воспользоваться тем, что медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины. Но возможно и другое решение.).

14. Записать уравнения прямых, содержащих стороны, медианы и высоты треугольника АВС, если А(1, 1), В(2,3), С(7, 4).

15. Записать параметрические и канонические уравнения прямой, содержащей медиану треугольника АВС к стороне ВС, если (3, -2, 2), (1, -3, 1), (2, 0, 4).

16. Составить канонические уравнения прямой, проходящей через точку (2, 0, –3) параллельно: а) вектору (2, –3, 5); б) прямой ; в) оси Ох; г) оси Оу; д) оси О .

17. Найти угол при вершине А треугольника АВС и расстояние от этой вершины до стороны ВС, если (3, -2), (1, -3), (2, 0).

18. Является ли треугольник АВС прямоугольным, если (3, -2, 2), (1, -3, 1), (2, 0, 4).

19. Найти векторное произведение векторов (8, -3, -4) и (-1, 1, 1).

20. Даны координаты вершин параллелограмма ABCD: (3, -2, 2), (1, -3, 1), (2, 0, 4), (0, -1, 3). Найти площадь параллелограмма ABCD.

21. Найти объём параллелепипеда, построенного на векторах 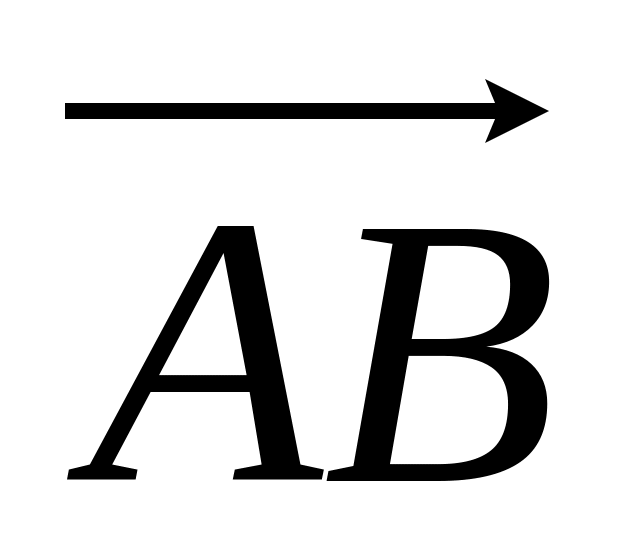, , , если (3, -2, 2), (1, -3, 1), (2, 0, 4), (6, - 4, 6).

22. Даны точки (3, 4, -4), В(-3, 2, 4), С(-1, -4, 4) и D(2, 3, -3). Определить, какие из них принадлежат линии пересечения поверхностей и .

23. Составить уравнение плоскости, проходящей через точки (3, -2, 2), (1, -3, 1), (2, 0, 4). Найти расстояние от точки (6, -4, 6) до этой плоскости.

24. Точка (1, -1, -1) является основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости.

25. Вычислить длину дуги между указанными точками следующих кривых:

а) , ;

в) ;

г) ;

26. Составить уравнения элементов сопровождающего трёхгранника кривой в указанной точке. Найти кривизну и кручение кривой в этой точке.

а)  при ;

б) в точке .

27. Записать уравнение касательной плоскости и нормали к поверхности , , в точке .

28. Записать уравнение касательной плоскости и нормали в точке поверхности , , .

29. Записать уравнение касательной плоскости и нормали в указанных точках к поверхностям, заданным следующими уравнениями:

1) в точке ;

2) в точке ;

3) в точке ;

4) в точке .