Скалярное произведение векторов. Длина вектора

Скалярным произведением векторов и на евклидовой плоскости или в евклидовом пространстве называется число . Квадрат длины вектора равен скалярному квадрату этого вектора: .

Скалярное произведение векторов и в трёхмерном евклидовом пространстве, заданных своими координатами в ортонормированном базисе, вычисляется по формуле: . Длина вектора вычисляется по формуле: . Для векторов на плоскости формулы аналогичны, только координат – две.

Пример. Длины векторов и равны , , а угол между ними . Найти длину вектора .

Решение.

Пример. Векторы и заданы своими координатами в ортонормированном базисе: , . Вычислить значение выражения .

Решение. , , , , .

Угол между векторами. Ортогональность векторов

Косинус угла между двумя ненулевыми векторами и может быть вычислен по формуле: .

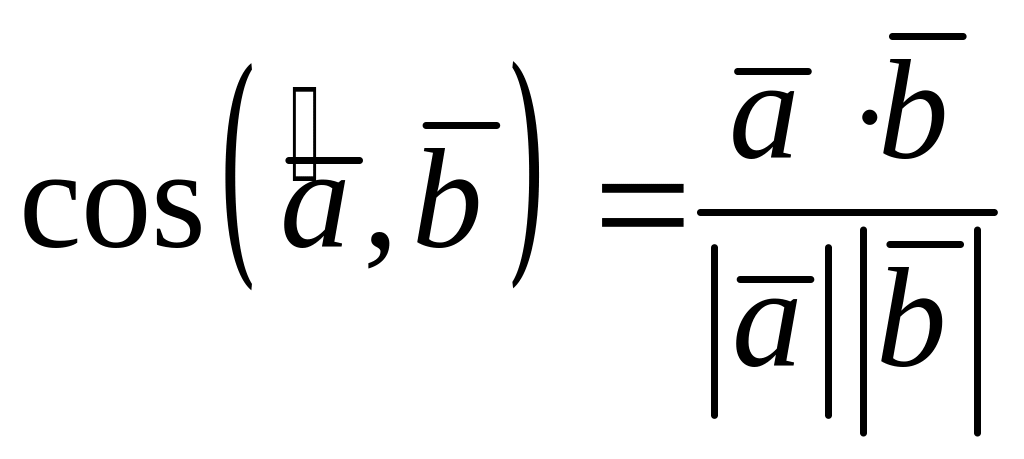Пример. Найти угол между векторами и .

Решение. .

Ответ: .

Два вектора называются ортогональными, если их скалярное произведение равно нулю (обозначение: ). Два вектора ортогональны тогда и только тогда, когда они перпендикулярны или хотя бы один из них нулевой.

Пример. Определить, при каком значении параметра ортогональны векторы и .

Решение. .

Таким образом, векторы и ортогональны при .

Ортонормированный базис

Определение. Базис -мерного евклидова пространства называется ортонормированным, если выполнены два условия:

1) , при всех (т. е. при );

2) , т. е. длины всех векторов базиса равны единице.

Из условий 1 и 2 следует, что векторы образуют базис -мерного векторного пространства. Поэтому, для того, чтобы проверить, что – базис -мерного евклидова пространства, достаточно проверить выполнение условий 1 и 2.

Пример. Определить, образуют ли векторы базис трёхмерного арифметического векторного пространства :

а) ; б) .

Решение. а) . Одно из условий определения не выполнено. Следовательно, векторы не образуют ортонормированный базис пространства .

б) ;

.

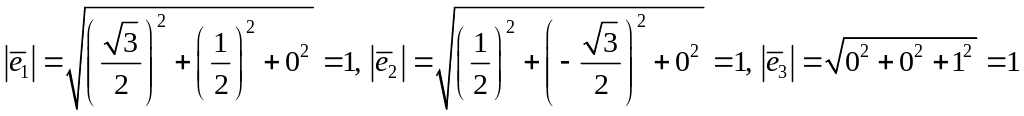Оба условия определения выполнены. Следовательно, – ортонормированный базис пространства .

Векторное произведение векторов

Векторное произведение векторов и в трёхмерном евклидовом пространстве, заданных своими координатами в ортонормированном базисе, вычисляется по формуле:

,

где , , – координатные орты. Геометрический смысл векторного произведения состоит в следующем: модуль векторного произведения равен площади параллелограмма, построенного на векторах и .

П ример. Найти площадь параллелограмма, построенного на векторах и .

Решение.

(определитель мы разложили по первой строке).

– площадь параллелограмма, построенного на векторах и .

Смешанное произведение векторов

Смешанное произведение векторов , и в трёхмерном евклидовом пространстве, заданных своими координатами в ортонормированном базисе, вычисляется по формуле:

.

Геометрический смысл смешанного произведения состоит в следующем: модуль смешанного произведения равен объёму параллелепипеда, построенного на векторах , и .

Пример. Вычислить объём параллелепипеда, построенного на векторах , и .

Решение.

.

– объём параллелепипеда, построенного на векторах , и .

Линейные операторы

Рассмотрим два линейных пространства, например Rⁿ размерности n и R^m размерности m.

 Определение. Если задан закон (правило), по которому каждому вектору пространства Rⁿ ставится в соответствие единственный вектор пространства R^m , то говорят, что задан оператор (отображение)  , действующий из Rⁿ в R^m , и записывают  .

Определение. Оператор называется линейным, если для любых векторов и пространства Rⁿ и любого числа λ выполняются соотношения: и  .

Если пространства Rⁿ и R^m совпадают, то оператор отображает пространство Rⁿ в себя. Именно такие операторы мы и будем рассматривать в дальнейшем.

Каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице n-го порядка соответствует линейный оператор в n-мерном пространстве.

Определение. Матрицей линейного оператора в базисе называется матрица , столбцы которой состоят из координат векторов в этом базисе.

Связь между вектором и его образом можно выразить в матричной форме уравнением  , где A – матрица линейного оператора ,  ,  - матрицы-столбцы из координат векторов и .

 Пример. Линейный оператор , действующий в пространстве R³, задан своей матрицей в базисе : . Найти образ вектора .

Решение. . Следовательно, .

Определим операции над линейными операторами.

Определение. Суммой двух линейных операторов  и  называется оператор  , определяемый равенством: для любого вектора . Произведением линейного оператора  на число λ называется оператор λ , определяемый равенством  для любого вектора . Произведением линейных операторов  и  называется оператор  , определяемый равенством:  для любого вектора .

Можно убедиться, что операторы  , λ ,  , полученные в результате этих операций, являются линейными.

Теорема. Пусть и – матрицы линейных операторов и  в некотором базисе. Тогда матрицами операторов , λ ,  в том же базисе являются матрицы , и соответственно.

Пример. Два линейных оператора  и , действующих в пространстве R , заданы своими матрицами в одном и том же базисе: , . Найти матрицы операторов –2,  + и  в том же базисе.

Согласно теореме, матрицы операторов –2,  + и  есть

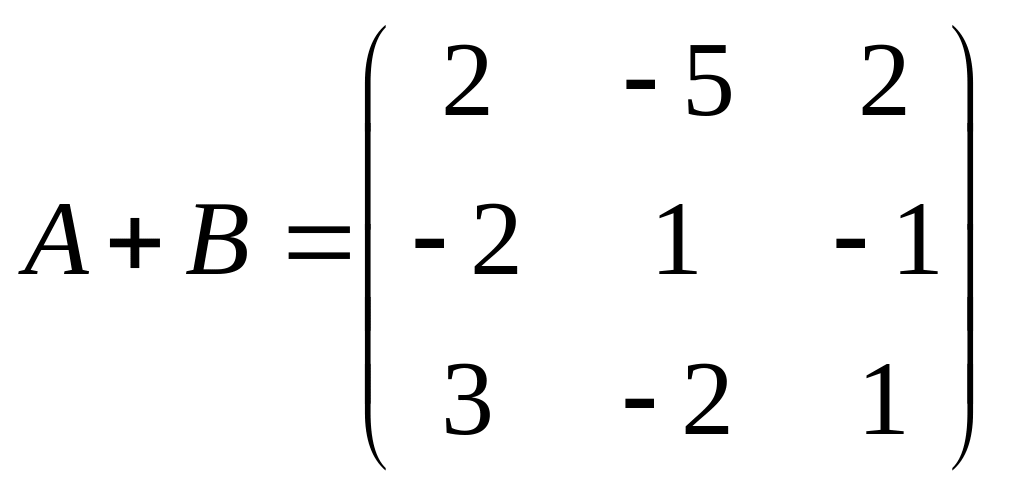, и соответственно.