Методические указания к решению задач по курсу «Алгебра и геометрия»

Составитель Толовиков М. И., к. ф.-м. н., доцент кафедры прикладной математики

Оглавление

Введение

Матрицы, определители, системы линейных уравнений

Операции над матрицами

Алгоритм Гаусса решения систем линейных уравнений

Методы вычисления определителей

Правило Крамера решения системы линейных уравнений

Обратная матрица. Её существование и вычисление

Элементы векторной алгебры

Понятие базиса. Координаты вектора в базисе. Линейная зависимость и линейная независимость векторов

Скалярное произведение векторов. Длина вектора

Угол между векторами. Ортогональность векторов

Ортонормированный базис

Векторное произведение векторов

Смешанное произведение векторов

Линейные операторы

Собственные значения и собственные векторы линейного оператора

Элементы аналитической геометрии

Координаты точки в декартовой системе координат. Координаты вектора

Расстояние между двумя точками

Деление отрезка в данном отношении

Параметрические и канонические уравнения прямой на плоскости и в пространстве

Общее уравнение прямой на евклидовой плоскости

Расстояние от точки до прямой на евклидовой плоскости

Параметрические уравнения плоскости в трёхмерном пространстве

Расстояние от точки до плоскости в евклидовом пространстве

Общее уравнение плоскости, проходящей через три точки

Элементы дифференциальной геометрии

Понятие кривой

Длина дуги кривой

Сопровождающий трёхгранник кривой

Кривизна и кручение кривой

Касательная плоскость и нормаль к поверхности

Задачи для самостоятельного решения

Рекомендуемая литература

Введение

В пособии приведены образцы решения простейших типовых задач по курсу «Алгебра и геометрия». Пособие предназначено, прежде всего, для студентов, обучающихся по заочной и сокращённой формам обучения и содержит материал, соответствующий стандарту по специальности «Программное обеспечение вычислительной техники и автоматизированных систем».

Матрицы, определители, системы линейных уравнений

Операции над матрицами

Выполнение операций над матрицами основано на их определениях.

Пусть A = (a_ij) – некоторая матрица и  – действительное число. Тогда по определению A = (a_ij), то есть при умножении матрицы A на число  все её элементы умножаются на число .

Пусть A = (a_ij), B = (b_ij) – матрицы одинакового размера. Тогда по определению их сумма есть матрица того же размера A + B = (a_ij + b_ij), то есть при сложении двух матриц складываются соответствующие их элементы.

Произведение матриц определяется следующим образом. Во-первых, произведение матрицы-строки на матрицу-столбец определяется как сумма произведений их соответствующих элементов: . Во-вторых, произведение матрицы размера на матрицу размера есть матрица размера , в которой элемент, стоящий на пересечении -й строки и -го столбца равен произведению -й строки матрицы A на -й столбец матрицы B.

Матрицей, транспонированной по отношению к матрице размера , называется матрица размера , строки которой равны соответствующим столбцам матрицы .

Пример. Выполнить операции над матрицами:

.

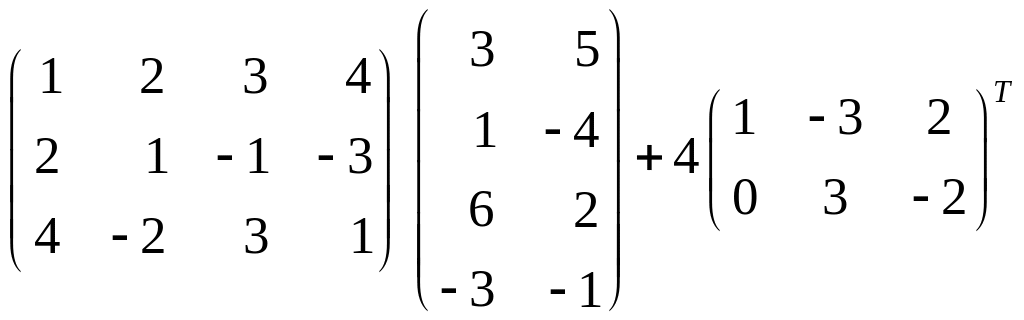Решение.

1)

= = ;

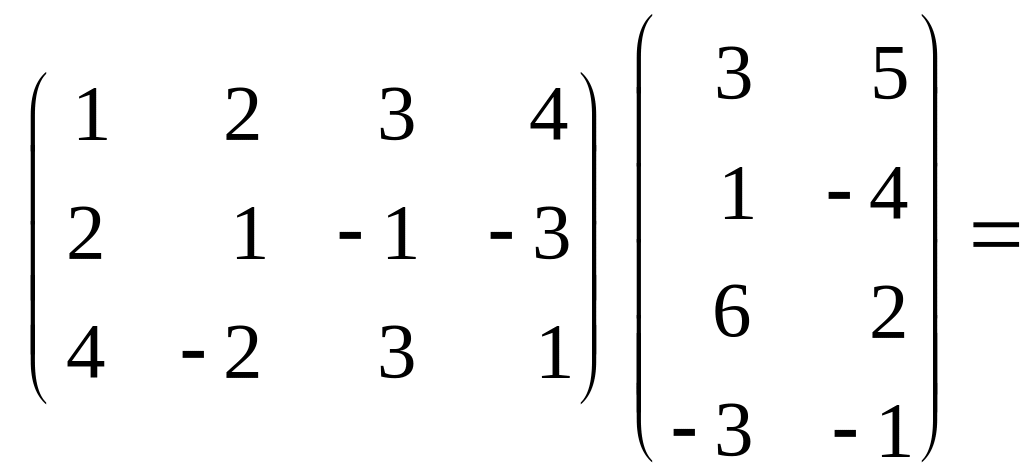
2) ;

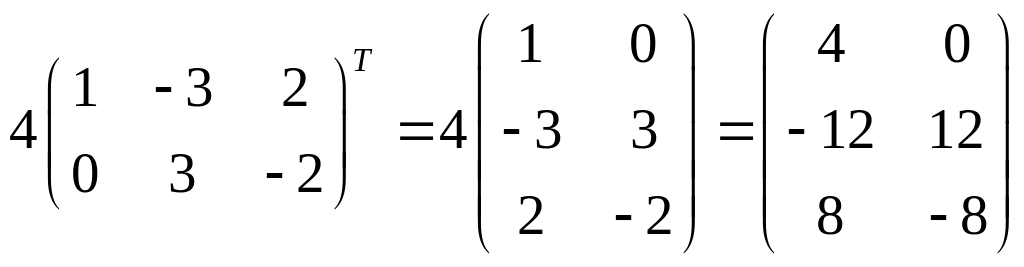3) .

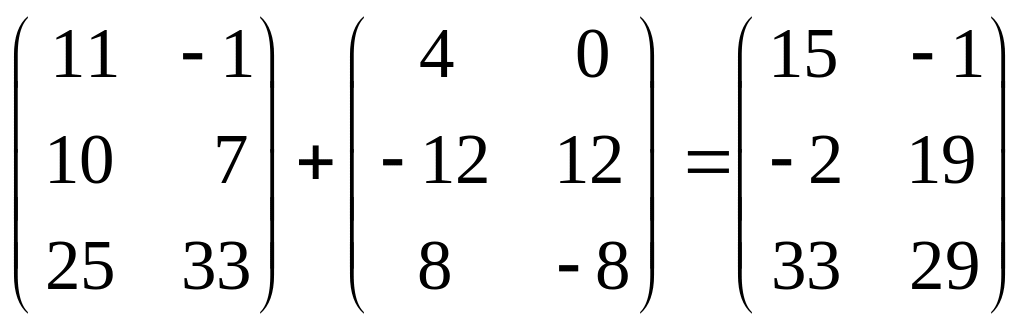Ответ: .

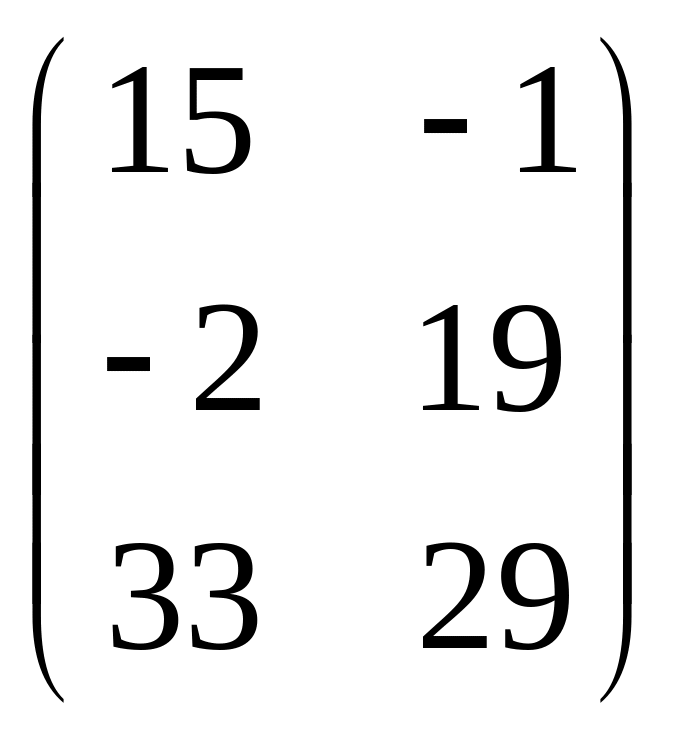Алгоритм Гаусса решения систем линейных уравнений

Рассмотрим систему из линейных уравнений с неизвестными:

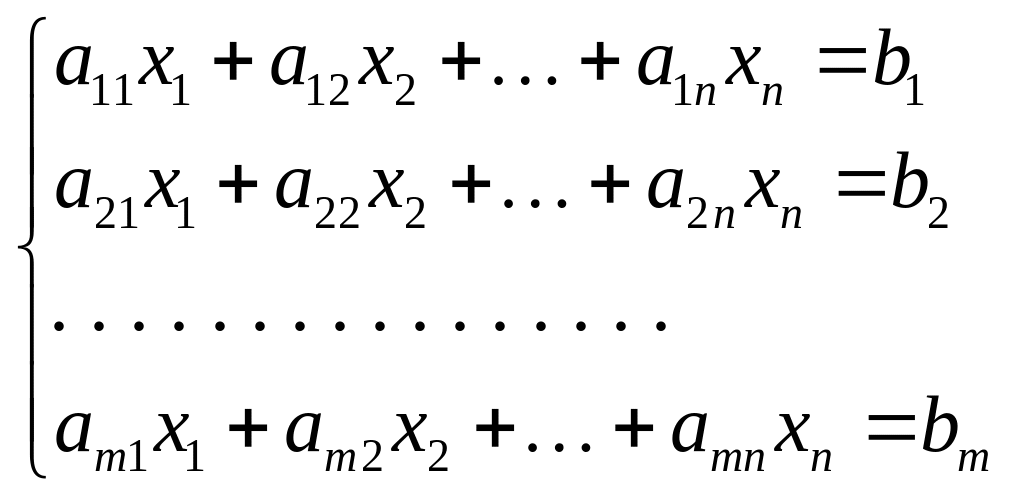(1)

Алгоритм Гаусса решения систем линейных уравнений состоит в следующем.

1. Записать расширенную матрицу системы: 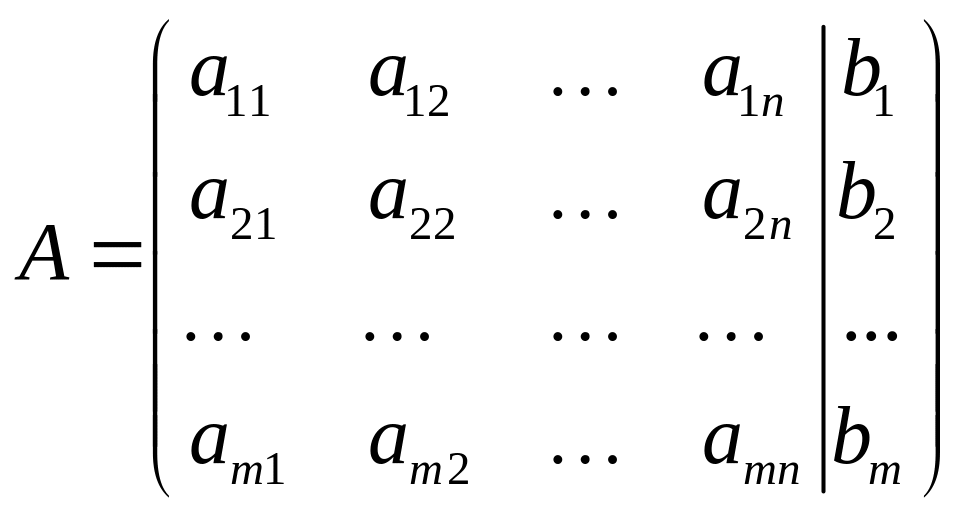. Если эта матрица нулевая, то решениями системы (1) являются все упорядоченные -ки действительных чисел 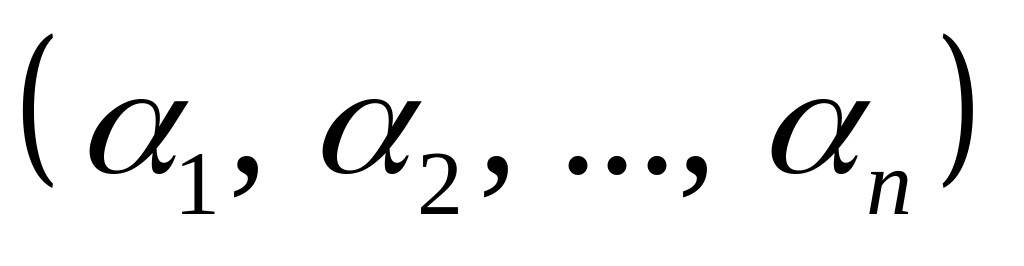. В противном случае перейти к шагу 2.

2. Перестановкой строк привести матрицу к виду , где 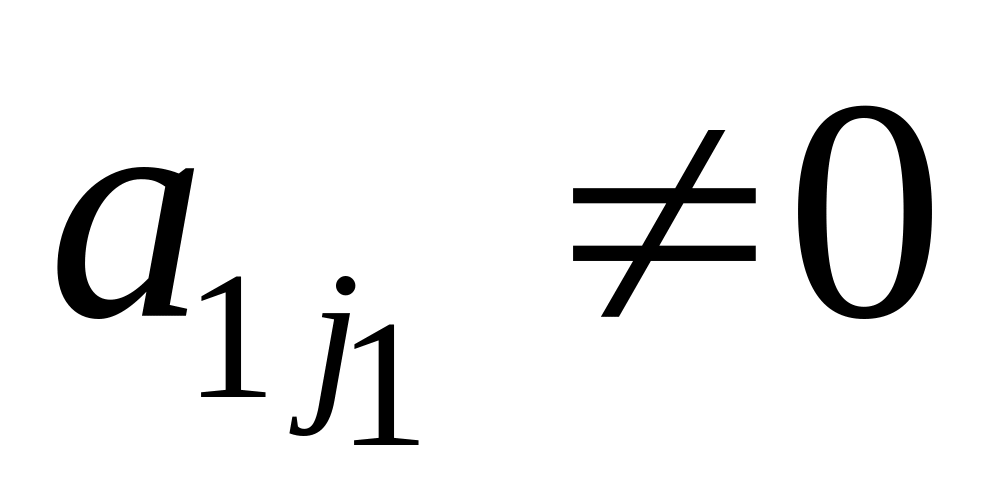. Для всех 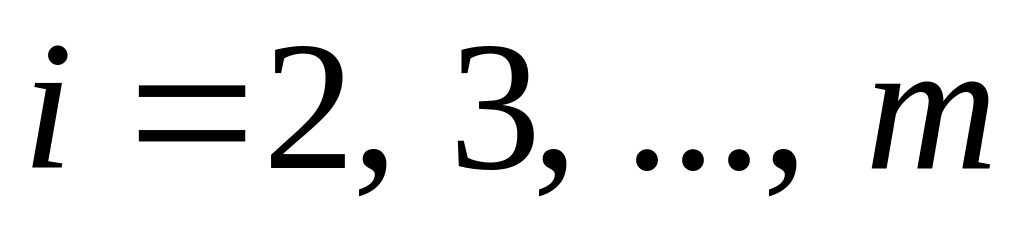прибавить к -й строке этой матрицы первую строку, умноженную на 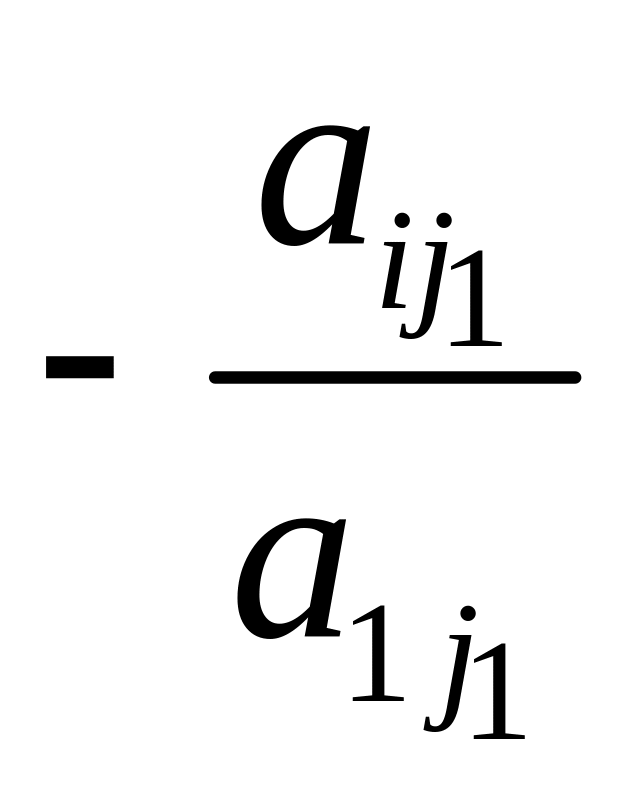. Полученная матрица будет иметь вид: 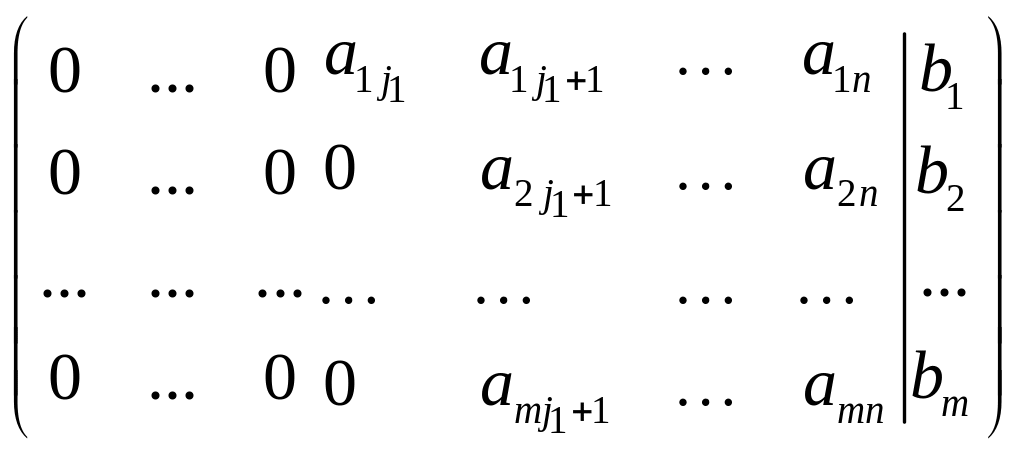. Если среди последних 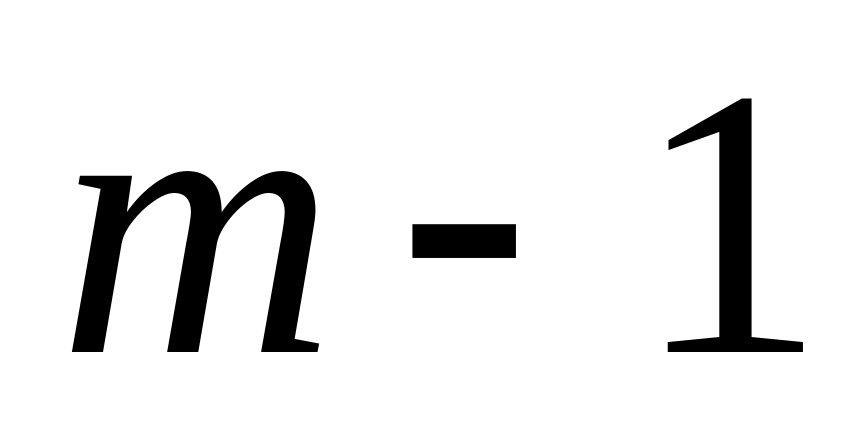строк этой матрицы есть ненулевые, то выполнить шаг 2 для этих строк. В противном случае перейти к шагу 3.

3. Матрица, полученная после выполнения всех действий на шаге 2, имеет вид

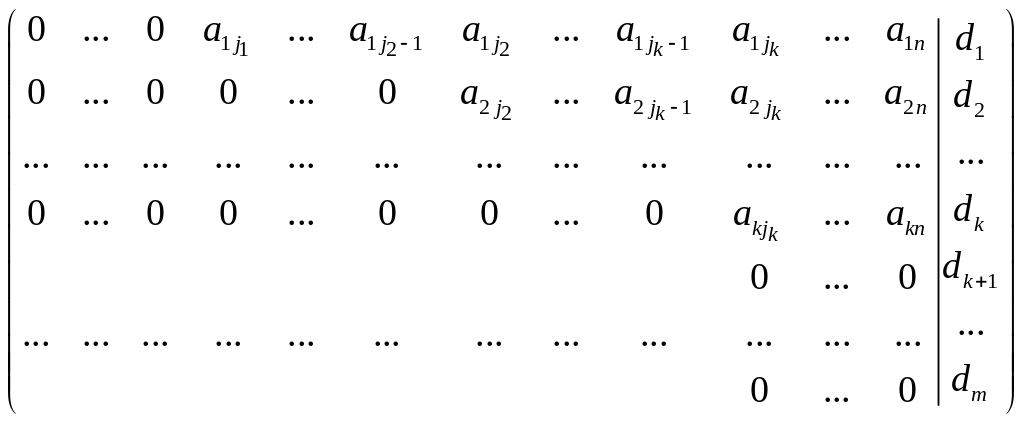, (2)

где , . Такая матрица называется матрицей ступенчатого вида. Если в матрице (2) есть строка вида , где , то система (2) не имеет решений (несовместна). Если в матрице (2) нет строк такого вида, то объявить неизвестные , , …, главными, а остальные (если они есть) – свободными. Придать свободным неизвестным произвольные числовые значения и выполнить обратный ход, который состоит в следующем.

Из уравнений системы с расширенной матрицей (2), начиная с -го, выразить последовательно , , …, через , подставляя каждый раз полученное выражение для во все предыдущие уравнения системы.

Если , то обратный ход даёт числовые значения всех неизвестных, и поэтому система имеет единственное решение. В противном случае система имеет бесконечно много решений, в которых свободные неизвестные принимают произвольные числовые значения , а значения главных выражаются через них по формулам, полученным в результате выполнения обратного хода.

Пример. Решить систему уравнений методом Гаусса.

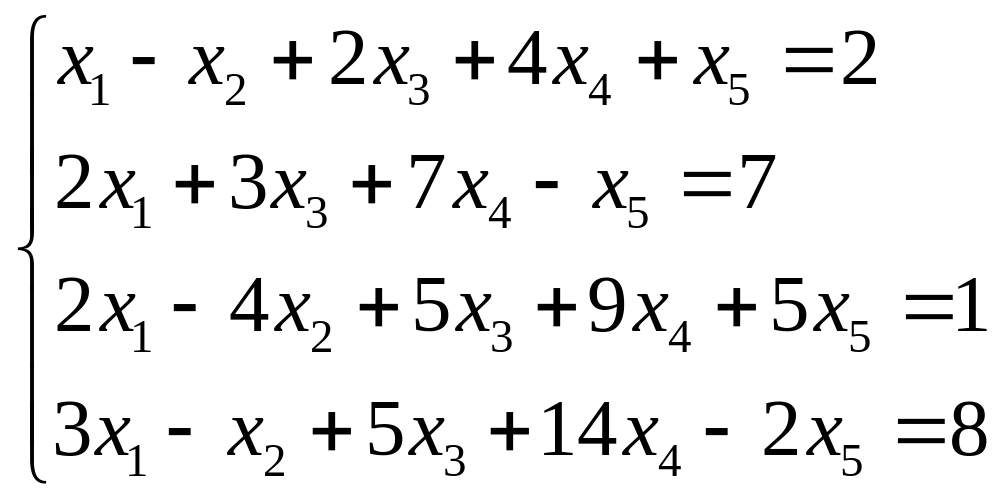
Решение. Записываем расширенную матрицу системы и приводим её к ступенчатому виду элементарными преобразованиями строк:

~ ~

~ ~ .

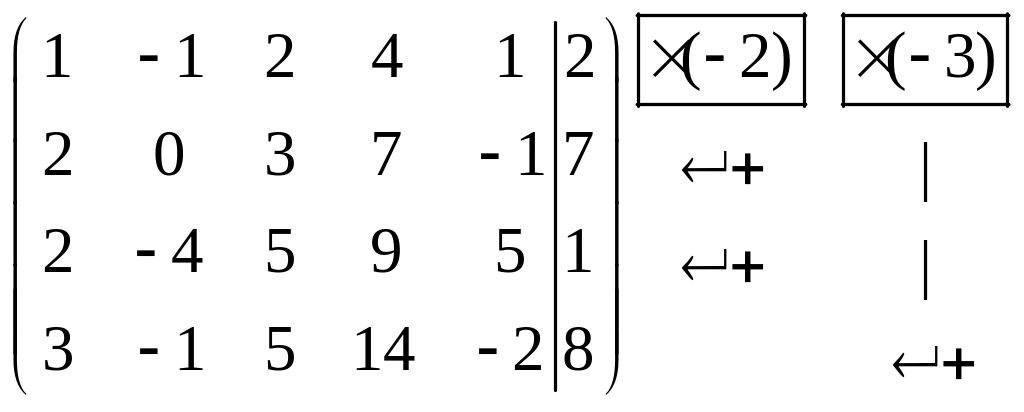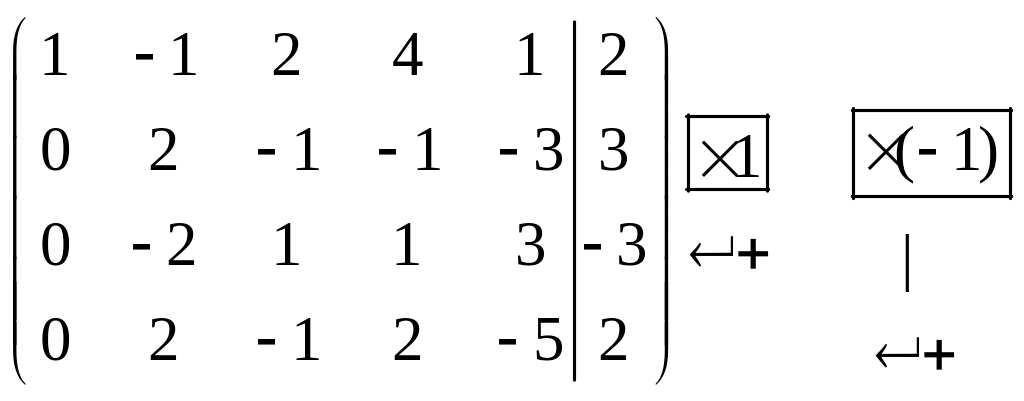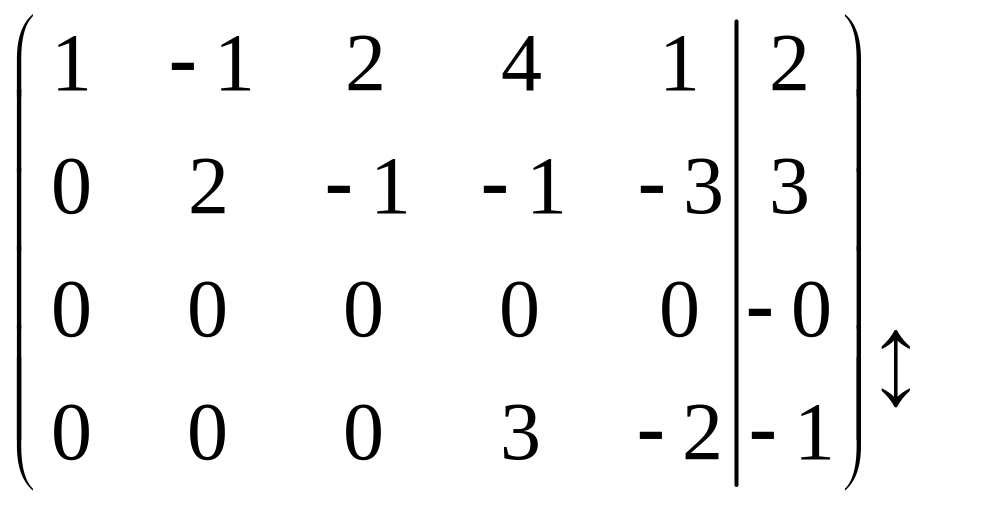Записываем систему с полученной расширенной матрицей ступенчатого вида (уравнения с нулевыми коэффициентами можно не записывать, так как при их отбрасывании множество решений системы не изменяется):

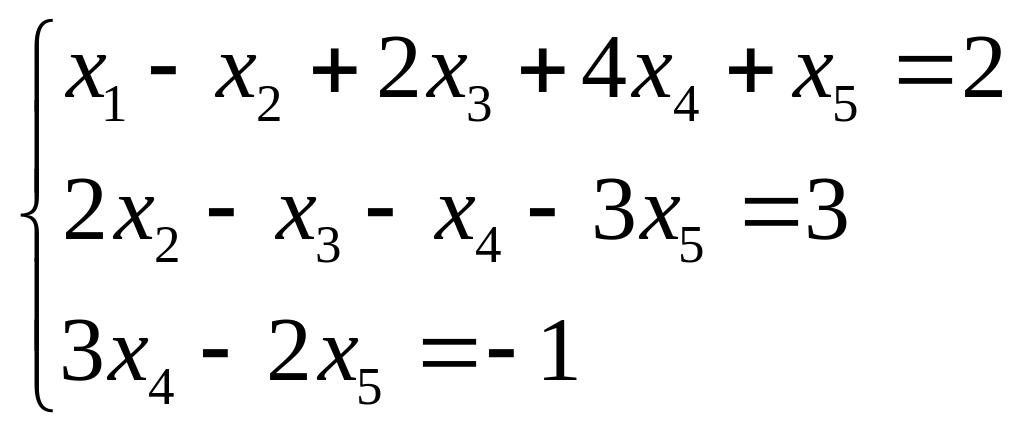
Главнее неизвестные: , , (первые по порядку номеров неизвестные с ненулевыми коэффициентами в уравнениях системы). Свободные неизвестные: , . Придадим свободным неизвестным произвольные числовые значения и и выполним обратный ход:

.

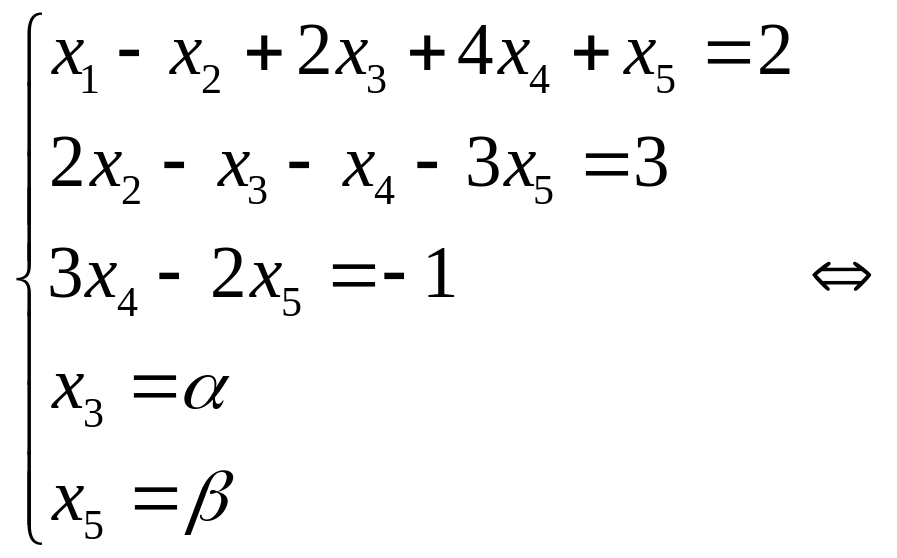
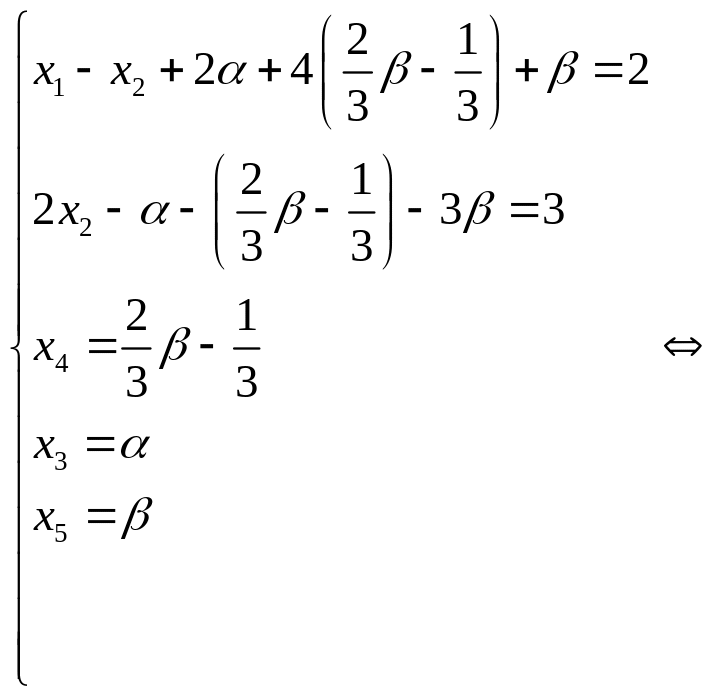
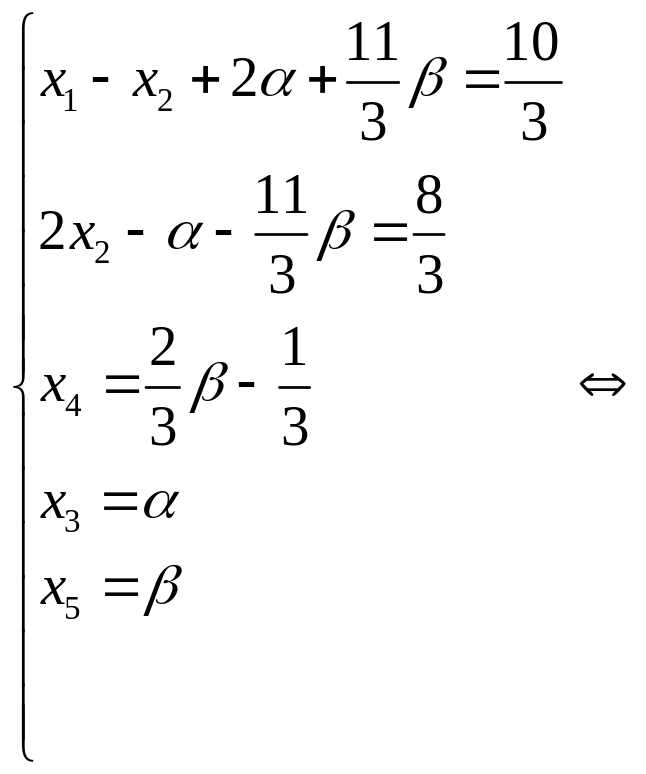
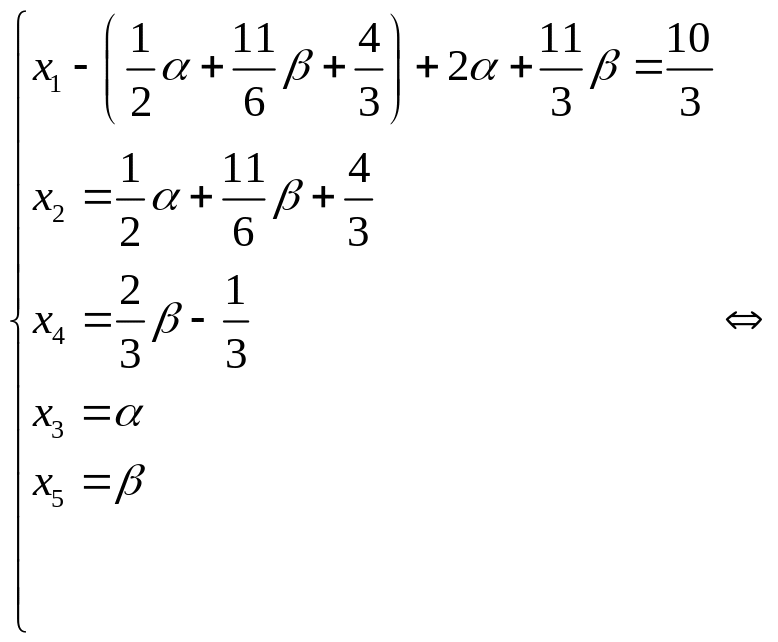
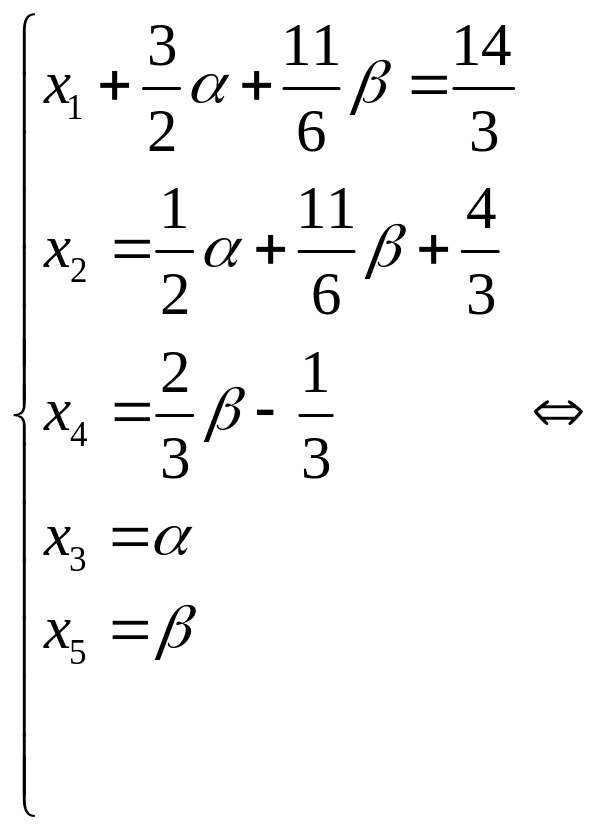
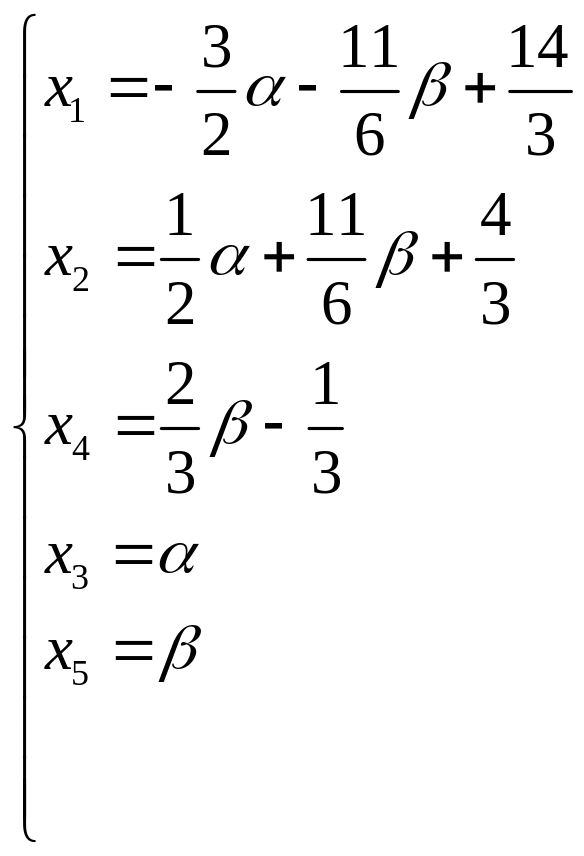Ответ: , .

Выполним проверку, подставив полученные выражения для неизвестных в исходную систему:

.

Раскрывая скобки и упрощая, получаем:

– верные числовые равенства.

Методы вычисления определителей

Основные методы вычисления определителей следующие:

1. по определению;

2. разложение по строке или по столбцу;

3. приведение матрицы определителя к треугольному виду с помощью элементарных преобразований строк и столбцов.

Первый метод основан на равенствах:

,

.

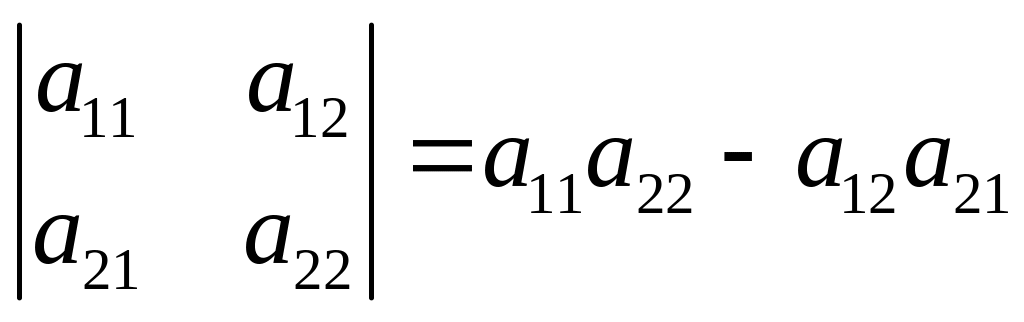Здесь в последнем равенстве три произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников с параллельной ей стороной: , берутся со знаком "", а три произведения элементов, стоящих на второй диагонали и в вершинах двух треугольников с параллельной ей стороной: , берутся со знаком "". Это правило называется правилом Сарюса.