Пример.

.

Чтобы описать второй метод, нам понадобится понятие алгебраического дополнения элемента квадратной матрицы.

Алгебраическим дополнением элемента квадратной матрицы называется число , где – определитель матрицы, полученной из вычеркиванием строки и столбца, на пересечении которых находится элемент .

Теорема (разложение определителя по элементам строки или столбца). Определитель матрицы равен сумме произведений элементов любой её строки (столбца) на их алгебраические дополнения.

Пример. Вычислить определитель, разложив его по элементам второй строки.

Решение.

.

(Определители третьего порядка мы вычислили первым методом.)

Третий метод основан на следующих свойствах определителей:

1. Если поменять местами две строки определителя (два столбца), то полученный определитель равен произведению исходного на .

2. Если одну из строк определителя умножить на какое-либо число, то полученный определитель равен произведению исходного на это число.

3. Если в определителе вместо любой строки записать сумму этой строки и любой другой строки, умноженной на некоторое число, то полученный новый определитель будет равен исходному.

4. Определитель треугольной матрицы равен произведению её диагональных элементов. (Треугольная матрица – это матрица, все элементы которой, стоящие выше или ниже главной диагонали, равны нулю.)

Метод приведения к треугольному виду состоит в следующем.

Приводим матрицу определителя к треугольному виду, действуя как в алгоритме Гаусса решения систем линейных уравнений. При этом на каждом шаге, используя свойства 1-3, определяем, как изменяется значение определителя. Когда матрица определителя приведена к треугольному виду, вычисляем значение определителя по свойству 4.

Пример. Вычислить определитель путём приведения к треугольному виду.

Решение.

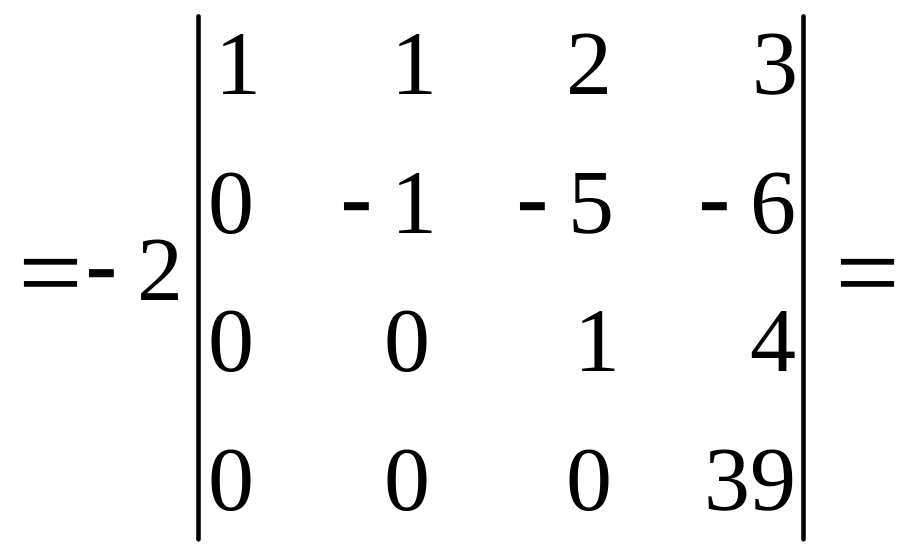
Правило Крамера решения системы линейных уравнений

Рассмотрим систему из линейных уравнений с неизвестными:

(3)

Определителем системы называется определитель матрицы из коэффициентов при неизвестных:

.

Теорема. Если определитель системы не равен нулю, то система (3) имеет ровно одно решение, которое может быть найдено по формулам: , , …, , где – определитель, полученный из заменой -го столбца столбцом свободных членов системы (3) .

Пример. Решить систему линейных уравнений по правилу Крамера:

.

Решение.

; , ,

.

Ответ: .

Обратная матрица. Её существование и вычисление

Пусть – квадратная матрица порядка . Матрицей, обратной к называется матрица такая, что , где – единичная матрица порядка (на главной диагонали матрицы находятся единицы, а все остальные её элементы равны нулю.)

Теорема. Матрица, обратная к квадратной матрице , существует тогда и только тогда, когда определитель матрицы отличен от нуля. Если существует, то она может быть найдена по формуле , где – определитель матрицы , – матрица из алгебраических дополнений элементов матрицы .

Пример. Вычислить матрицу обратную к :

Решение.

.

.

Выполним проверку:

.

Равенство можно не проверять, так как оно следует из равенства (все матрицы квадратные одного и того же порядка).

Элементы векторной алгебры

Понятие базиса. Координаты вектора в базисе. Линейная зависимость и линейная независимость векторов

Определение. Говорят, что векторы образуют базис векторного пространства , если любой вектор единственным образом линейно выражается через векторы : . Коэффициенты называются при этом координатами вектора в базисе (обозначение: ). Число векторов во всех базисах векторного пространства одинаково и называется размерностью этого пространства.

Операции над векторами, заданными своими координатами в одном и том же базисе производятся покоординатно.

Теорема. Пусть и – координаты векторов и в базисе . Тогда и – координаты векторов и в этом базисе ( ).

Определение. Векторы называются линейно зависимыми, если уравнение имеет решение , в котором не все равны нулю. Если это уравнение имеет только нулевое решение: , то векторы называются линейно независимыми.

Пример. Определить, являются ли векторы в пространстве линейно зависимыми. Если да, то указать нетривиальную линейную комбинацию этих векторов равную нулевому вектору.

а) , , .

Решение.

.

Решая эту систему методом Гаусса, получаем: . Это даёт ненулевое решение уравнения . Следовательно, векторы , и линейно зависимы. Выбирая, например , получаем нетривиальную линейную комбинацию векторов , и равную нулевому вектору: .

б) , , .

Решение. Как и в предыдущем случае, составляем и решаем соответствующую систему линейных уравнений: .

Таким образом, уравнение имеет только нулевое решение . Следовательно, векторы , и линейно независимы.

Сформулируем теперь критерий линейной независимости векторов в -мерном векторном пространстве.

Пусть – координаты векторов в некотором базисе -мерного векторного пространства. Как можно увидеть из решения предыдущего примера, справедлива следующая теорема.

Теорема. Векторы линейно независимы тогда и только тогда, когда определитель из их координат отличен от нуля.

Например, , поэтому векторы , , линейно зависимы. А векторы , , линейно независимы, так как .

Критерий базиса даёт следующая теорема.

Теорема. Векторы образуют базис -мерного векторного пространства тогда и только тогда, когда они линейно независимы.

Пример. Определить, образуют ли векторы базис пространства . Если да, то разложить вектор по этому базису.

Решение. , следовательно векторы линейно независимы. Так как этих векторов три и пространство трёхмерно, то векторы образуют базис пространства . Разложим вектор по этому базису:

.

Таким образом, , т. е координаты вектора в базисе равны .