Общее уравнение прямой на евклидовой плоскости
Прямую
на евклидовой
плоскости
можно задать с помощью принадлежащей
ей точки
и ненулевого вектора
,
перпендикулярного ей. Вектор
называется нормальным вектором прямой.
Общим
уравнением прямой на плоскости называется
уравнение вида
,
где
или
.
В прямоугольной декартовой системе
координат любое уравнение такого вида
задаёт на евклидовой плоскости прямую,
и любую прямую можно задать уравнением
такого вида. При этом
– нормальный вектор данной прямой.
Уравнение прямой
,
проходящей через точку
с нормальным вектором
,
имеет вид:
.
П
ример.
Записать общее уравнение прямой,
содержащей высоту
треугольника
с вершинами
,
,
.
Решение. 
Вектор
перпендикулярен прямой
,
значит является нормальным вектором
этой прямой. Точка
принадлежит прямой
.
Следовательно, уравнение прямой
имеет вид
.
Ответ:
.
Расстояние от точки до прямой на евклидовой плоскости
Расстояние от точки до прямой , заданной общим уравнением , вычисляется по формуле:
.
Пример. Вычислить длину высоты треугольника с вершинами , , .
Решение. Вначале запишем уравнение прямой :
.
Длина высоты равна расстоянию от точки до прямой :
.
Параметрические уравнения плоскости в трёхмерном пространстве
Плоскость в пространстве можно задать
1) парой неколлинеарных векторов
,
параллельных этой плоскости, и точкой
,
лежащей на ней; 2) тремя точками
,
и
,
лежащими в этой плоскости и не лежащими
на одной прямой.
Параметрические уравнения плоскости
параллельной неколлинеарным векторам
и
,
проходящей через точку
,
имеют вид:
.
Здесь
– текущие координаты точки,
и
– параметры. Уравнения плоскости,
проходящей через три точки
,
и
,
не лежащие на одной прямой, можно получить
следующим образом.
Векторы
и
не коллинеарны и параллельны данной
плоскости. Поэтому их можно взять в
качестве векторов
и
,
а в качестве точки, лежащей в данной
плоскости, взять точку
.
Пример. Записать параметрические
уравнения плоскости, проходящей через
точки
,
,
.
Решение.
,
– направляющие векторы данной плоскости.
– параметрические уравнения данной
плоскости.
Общее уравнения плоскости в евклидовом пространстве
Плоскость
в
евклидовом
пространстве
можно задать с помощью принадлежащей
ей точки
и ненулевого вектора
,
перпендикулярного ей. Вектор
называется нормальным вектором плоскости.
Общим
уравнением плоскости называется
уравнение вида
,
где
или
или
.
В прямоугольной декартовой системе
координат любое уравнение такого вида
задаёт плоскость, и любую плоскость
можно задать уравнением такого вида.
При этом
– нормальный вектор данной плоскости.
Уравнение плоскости
,
проходящей через точку
с нормальным вектором
,
имеет вид:
.
Пример. Точка
является основанием перпендикуляра,
опущенного из начала координат на
плоскость
.
Записать общее уравнение плоскости
.
Решение. Вектор
перпендикулярен плоскости
и поэтому является нормальным вектором
этой плоскости (
– начало координат). Точка
принадлежит плоскости
.
Следовательно, общее уравнение этой
плоскости имеет вид:
.
Ответ:
.
Общее уравнение плоскости, проходящей через три точки
Общее уравнение плоскости, проходящей
через три точки
,
и
,
не лежащие на одной прямой, имеет вид:
.
Пример. Записать общее уравнение плоскости, проходящей через точки , , .
Решение. Уравнение имеет вид:
Ответ:
Расстояние от точки до плоскости в евклидовом пространстве
Расстояние от точки до плоскости , заданной общим уравнением , вычисляется по формуле:
.
Пример. Найти длину высоты
пирамиды
с вершинами в точках
,
,
,
.
Решение. Запишем вначале уравнение плоскости :
.
Длина высоты
равна расстоянию от точки
до плоскости
:
.
Элементы дифференциальной геометрии
Понятие кривой
Пусть I - интервал числовой прямой, – трёхмерное евклидово пространство.
Определение. Говорят, что в евклидовом
пространстве
задана непрерывная кривая ,
если задано непрерывное отображение
f :
.
Отображение f
называется при этом параметризацией
кривой .
Отображение f может быть задано уравнениями:
, (6)
где
– координаты точки
.
Эти уравнения можно записать в векторной
форме:
,
где
– радиус-вектор точки
.
Длина дуги кривой
Длина дуги кривой, заданной
параметрическими уравнениями (6) на
отрезке
вычисляется по формуле
.
Пример.
Винтовая линия задана параметрическими
уравнениями:
,
.
Найти длину дуги этой кривой,
заключенной между точками
и
.
Решение.
,
,
,
.
Ответ:
Сопровождающий трёхгранник кривой
Пусть гладкая кривая в пространстве
задана векторным параметрическим
уравнением
.
К каждой регулярной точке кривой можно
каноническим образом присоединить
прямоугольную декартову систему
координат (регулярная точка – это точка,
в которой векторы
и
неколлинеарны). Началом координат
является данная точка
.
Прямые, на которых лежат оси координат,
и плоскости, проходящие через координатные
оси, имеют специальные названия.
Совокупность этих трёх прямых и плоскостей
называется сопровождающим трёхгранником
кривой. Элементы сопровождающего
трёхгранника следующие.
1. Касательная к кривой. Её направляющий
вектор есть вектор
,
поэтому канонические уравнения
касательной в точке, которая соответствует
значению параметра
,
имеют вид:
.
2. Нормальная плоскость. Она перпендикулярна
касательной к кривой. Поэтому её
нормальный вектор есть
,
а общее уравнение нормальной плоскости
имеет вид:
.
3. Бинормаль. Её направляющий вектор
есть вектор
.
4. Соприкасающаяся плоскость. Она перпендикулярна бинормали, поэтому её нормальный вектор есть .
5. Главная нормаль. Её направляющий
вектор есть
.
6. Спрямляющая плоскость. Она перпендикулярна главной нормали, поэтому её нормальный вектор есть .
Пример. Составить уравнения элементов
сопровождающего трёхгранника кривой
при
.
Решение. Значению параметра соответствует точка кривой М(-2, 3, -4).
1.
;
в точке М:
.
Используя канонические уравнения
касательной, получаем:
.
2. Уравнение нормальной плоскости:
.
3.
,
.
.
Записываем канонические
уравнения бинормали как уравнения
прямой, проходящей через точку М(-2, 3, -4)
с направляющим вектором
:
.
4. Уравнение соприкасающейся плоскости
запишем как уравнение плоскости с
нормальным вектором
,
проходящей через точку М(-2, 3, -4):
.
5.
.
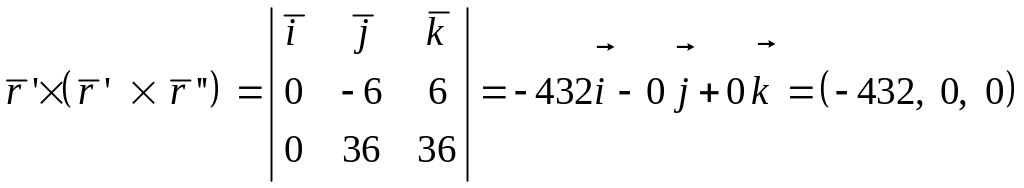Канонические уравнения
главной нормали записываем как уравнения
прямой, проходящей через точку М(-2, 3, -4)
с направляющим вектором
:
.
6. Уравнение спрямляющей плоскости
запишем как уравнение плоскости с
нормальным вектором
,
проходящей через точку М(-2, 3, -4):
.
Кривизна и кручение кривой
Кривизна и кручение кривой вычисляются
соответственно по формулам:
,
.
Пример. Вычислить кривизну и кручение кривой при (см. предыдущий пример).
Решение.
– кривизна кривой;
,
,
,
,
– кручение кривой в точке М(-2, 3, -4).
Касательная плоскость и нормаль к поверхности
Пусть задано непрерывное отображение плоской области E в трёхмерное евклидово пространство . Тогда говорят, что дана поверхность в евклидовом пространстве, а данное отображение называют её параметризацией.
Существует три основных способа задания поверхности.
1) Параметрическое задание. При этом способе поверхность задаётся тремя уравнениями вида:
,
,
,
(7)
или одним векторным параметрическим уравнением
,
(8)
где
,
функции
,
,
определены в плоской области E.
То, что уравнения (7) задают поверхность
S означает следующее:
точка (
,
,
)
лежит на поверхности при любых значениях
параметров
,
и любая точка этой поверхности получается
при некоторых значениях параметров
.
2) Явное задание. При этом способе поверхность задаётся уравнением вида
,
(9)
где f – действительная
функция, определённая в плоской области
E. Точка с координатами
пробегает поверхность S,
когда точка
пробегает область E.
3) Неявное задание. При этом способе поверхность задаётся уравнением вида
,
(10)
где
– действительная функция, определённая
в некоторой области пространства
.
Точка
лежит на поверхности тогда и только
тогда, когда её координаты удовлетворяют
уравнению (10).
Пусть S – поверхность в евклидовом пространстве и M – точка этой поверхности. Если поверхность гладкая, то в любой её точке определена касательная плоскость (см. рисунок) и нормаль к поверхности. Нормаль перпендикулярна касательной плоскости и проходит через точку касания.
Если поверхность S
задана уравнениями вида (7), то уравнения
касательной плоскости и нормали к этой
поверхности в точке
имеют вид
(11)
(общее уравнение касательной плоскости
в точке
);
(каноническое уравнение нормали в точке
).
Если поверхность S
задана уравнением вида (9), то уравнение
касательной плоскости и нормали в точке
,
лежащей на поверхности S
(т. е. такой, что
),
имеют вид
(общее уравнение касательной плоскости
в точке
);
(каноническое уравнение нормали в точке ).
Если поверхность S
задана уравнением вида (10), то уравнение
касательной плоскости и нормали в точке
,
лежащей на поверхности S
(т. е. такой, что
),
имеют вид
(общее уравнение касательной плоскости в точке );
(канонические уравнения нормали в точке ).
Пример. Записать уравнение касательной
плоскости и нормали к поверхности
,
,
в точке
.
Решение. Найдём
значения параметров
и
,
соответствующие точке
:
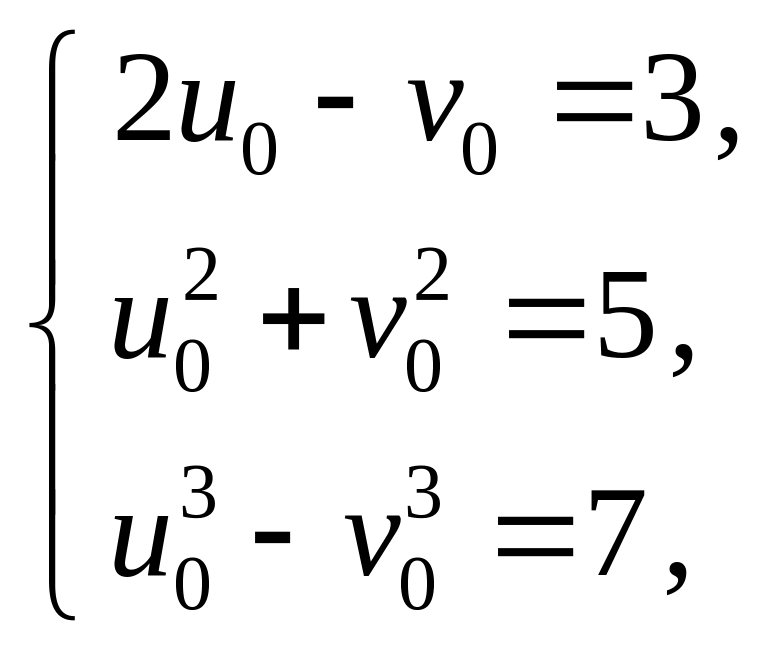
Далее,
,
,
,
,
,
,
,
,
,
,
,
.
Подставляя эти значения в (11), получаем
общее уравнение касательной плоскости
в точке
:
.
Так как нормаль проходит через точку
касания и перпендикулярна касательной
плоскости, то её канонические уравнения
имеют вид:
.