2.4. Графическое решение уравнений и систем уравнений

Средствами Excel можно найти приближенное графическое решение уравнения f(x) = 0 (абсциссу точки пересечения графика с осью Х) и системы уравнений с двумя неизвестными (координаты точки пересечения графиков, соответствующих уравнениям системы). При этом точность решения определяется величиной шага дискретизации (чем меньше шаг, тем точность выше).

Пример 2.6. Найти корень уравнения х – cosx = 0 с точностью 0,0001.

Сначала необходимо подготовить таблицу значений функции f(x), стоящей в левой части уравнения, на отрезке, где лежит корень. Проанализировав функцию f(x) = х – cosx, можно сделать вывод о том, что корень лежит на отрезке [0;1], так как при х = 0 значение функции f(x) равно –1, а при х ≥ 1 функция принимает положительные значения (|cosx| ≤ 1).

Создадим таблицу значений этой функции на выбранном отрезке с шагом, допустим, 0,2. В 1-ю строку (или столбец) введем значения аргумента: 0, 0,2, …, 1. В ячейку В2 введем формулу =В1–COS(В1), которую затем скопируем в ячейки С2:G2 (рис. 2.9).

	A	B	C	D	E	F	G
1	х	0	0,2	0,4	0,6	0,8	1
2	f(x)	-1	-0,79007	-0,52106	-0,22534	0,10329	0,45970

Рис. 2.9

Точечная диаграмма, построенная по данным этой таблицы, представлена на рис. 2.10.

Рис. 2.10

Из графика видно, что корень  0,75. Подставив найденное значение корня в левую часть уравнения, определим погрешность вычисления: 0,018311. В задании требуется найти корень с точностью 0,0001, поэтому надо продолжить уточнение корня. Для этого нужно создать таблицу на отрезке [0,7;0,8] с шагом 0,02 и построить Точечную диаграмму (рис. 2.11). Из графика видно, что функция пересекает ось Х в точке  0,74. Погрешность вычислений равна 0,001531, следовательно, надо создавать новую таблицу или корректировать предыдущую, сужая отрезок и уменьшая шаг. Этот процесс надо продолжать до тех пор, пока погрешность вычислений не станет по модулю меньше 0,0001.

Рис. 2.11

В Excel есть эффективный метод решения нелинейных уравнений — Подбор параметра. Подбор параметра — средство Excel, позволяющее решать так называемую обратную задачу, когда требуется, меняя значение одного из исходных данных (параметров), получить заданное значение результата. При этом результат решения задачи должен быть задан в целевой ячейке формулой, содержащей ссылку на изменяемую ячейку с параметром. При подборе параметра его значение изменяется так, чтобы результат в целевой ячейке стал равным заданному числу.

Сформируем таблицу, в ячейку В1 которой запишем значение корня, а в ячейку В2 формулу =В1–COS(B1) (рис. 2.12, а). Вызовем команду: Данные  группа Работа с данными  Анализ «что–если»  Подбор параметра и в появившемся диалоговом окне заполним поля:

• Установить в ячейке: В6;

• Значение: 0;

• Изменяя значение ячейки: В5.

П осле выполнения команды в ячейках В5 и В6 появятся вычисленные значения (рис. 2.12, б).

	A	B			А	В
5	x	-0,74		5	х	0,7390838
6	f(x)	0,001531		6	f(x)	-2,19892E-06

а б

Рис. 2.12

Если уравнение имеет один корень, то в качестве начальной точки для команды Подбор параметра можно взять любую точку отрезка.

Пример 2.7. Графически решить систему уравнений

в диапазоне x  [0;1].

Преобразуем уравнения таким образом, чтобы в первом и во втором уравнении переменная y выражалась через х. Первое уравнение будет записано так: y = ln(x + 0,55), а второе уравнение: y = (x – 0,8)/3. Подготовим таблицу с тремя строками (рис. 2.13):

	A	B	C	D	E	F	G
1	x	0	0,2	0,4	0,6	0,8	1
2	y=ln(x+0,55)	-0,59784	-0,28768	-0,05129	0,13976	0,30010	0,43826
3	y=(x-0,8)/3	-0,26667	-0,20000	-0,13333	-0,06667	0,00000	0,06667

Рис. 2.13

По данным этой таблицы построим Точечную диаграмму, представленную на рис. 2.14.

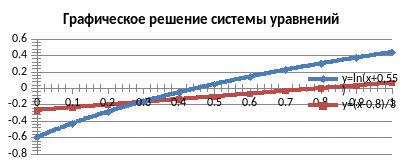
Рис. 2.14

Р ешением системы являются координаты точки пересечения кривых: x  0,3, y  –0,17. Если бы при подготовке таблицы использовали более мелкий шаг аргумента, то получили бы более точное решение системы. Определим погрешность вычисления и уточним решение с помощью команды Подбор параметра. Для этого сформируем таблицу, представленную на рис. 2.15, а.

	A	B			A	B
6	x	0,3		6	x	0,2950927
7	y=ln(x+0,55)	-0,16252		7	y=ln(x+0,55)	-0,16830895
8	y=(x-0,8)/3	-0,16667		8	y=(x-0,8)/3	-0,16830243
9	Погрешность	0,00415		9	Погрешность	-6,5Е-06

а б

Рис. 2.15

Погрешность вычисляем по формуле =ABS(В7–В8). Для уточнения полученного решения вызовем команду: Данные  группа Работа с данными  Анализ «что–если»  Подбор параметра и в появившемся диалоговом окне заполним поля:

• Установить в ячейке: В9;

• Значение: 0;

• Изменяя значение ячейки: В6.

Результат работы команды Подбор параметра представлен на рис. 2.15, б.