
- •32. Правило Лопиталя
- •12.Операция над пределами последовательностей.
- •13.Пределы функции в точке. Односторонние пределыв.
- •15.Бесконечно малые и бесконечно большие функции.
- •16.Замечательные пределы.(I) зам предел: (II) зам предел : (III)зп: (IV)зп: (V) зп:
- •18.Непрерывность функции одной переменньой в точке .Односторонняя непрерывность
- •23 Точки разрыва функции и их классификация
- •32. Правило Лопиталя
- •33. Локальный и глобальный экстремум функции
- •35. Асимптоты графика функций.
- •36. Алгоритм полного исследования функции для построения её графика.
- •37. Функции двух переменных, геометрический смысл. Линии уровня поверхности.
- •38. Предел и непрерывность функции двух переменных.
- •39.Частные производные. Уравнение касательной плоскости и нормали к поверхности.
- •44.Исследование функции 2х перемен-ых на локальный экстремум.
- •49. Выделение целой части неправильной алгебраической дроби.
- •58.Определенный интеграл с переменным верхним пределом и его свойства
- •71.Простейшие св-ва рядов.Необходимый признак сходимости.
- •72.Признаки сх-ти рядов с положительными членами.
- •73.Знакопеременные ряды,абсолютная и условная сх-ти
- •74.Признак Лейбница сходимости знакочередующегося ряда.
- •75.Функциональные ряды.Нахождение области сх-ти функционального ряда.
- •76.Степенные ряды.Теорема Абеля.
- •77.Радиус и интервал сх-ти степенного ряда.
- •78.Дифференцирование и интегрирование степенных рядов.
49. Выделение целой части неправильной алгебраической дроби.
Если числитель меньше знаменателя, такая дробь называется правильной. В противном случае (т.е. когда числитель больше или хотя бы равен знаменателю) дробь называется неправильной, и в ней можно выделить целую часть. Чтобы выделить целую часть в неправильной дроби, надо выполнить три простых шага: 1. Найдите, сколько раз знаменатель помещается в числителе. Другими словами, найдите максимальное целое число, которое при умножении на знаменатель все равно будет меньше числителя (в крайнем случае — равно). Это число и будет целой частью, поэтому записываем его спереди; 2. Умножьте знаменатель на целую часть, найденную в предыдущем шаге, а результат вычтите из числителя. Полученный «огрызок» называется остатком от деления, он всегда будет положительным (в крайнем случае — ноль). Записываем его в числитель новой дроби;3. Знаменатель переписываем без изменений.
50.Разложение правильной алгебраической дроби на простейшие. Опр.1-рацион. дробь наз-ся правильной, если степень многочлена числителя меньше степени многочлена знаменателя. Теорема. Всякую правильную рацион.дробь можно представить в виде суммы простейших дробей, причём единственным образом. Правильную часть рацион.дроби разложим на сумму простейших дробей. Вид разложения зависит от корней знаменателя. 1.Все корни знаменателя действит-е простые.таким образом, корням в разложении соответствуют дроби первого типа: Pn(x)/Qm(x)=Pn(x)/(x-a1)(x-a2)…(x-am)=A1/x-a1+A2/x-a2+…+Am/x-am. (n<m) 2.Среди действит. корней знаменателя есть кратные корни, кот-м соответствуют дроби первого и второго типа: PN(x)/Qm(x)=Pn(x)/(x-a1)k1(x-a2)k2(x-a3)…(x-ae)=Ak1/(x-a1)k1+Ak-1/(x-a1)k1-1+…+A2/(x-a1)2+A1/x-a1+Bk2/(x-a2)k2+Bk2-1/(x-a2)k2-1+…+B2/(x-a2)2+B1/(x-a2)+C/x-a3+…+D/x-ae. 3.Знаменатель содержит комплексно сопряжённые корни простые, кот.соответствуют дроби 3-го типа. Pn(x)/Qm(x)=Pn(x)/(x2+px+q)(x2+bx+c)(x-x1)…(x-xe)=Ax+B/x2+px+q + Cx+D/x2+bx+c + L/x-x1 +…+ M/x-xe. (n<m, D=p2-4q<0, D=b2-4c<0). 4. Знаменатель содержит кратные комплексно сопряжённые корни, кот.соответствуют дроби 3-го и 4-го типа. Pn(x)/Qm(x)=Pn(x)/(x2+px+q)k(x-x1)…(x-xe)=Akx+Bk/(x2+px+q)k+ Ak-1+Bk-1/(x2+px+q)k-1 +…+ A2x+B2/(x2+px+q)2 + A1x+B1/x2+px+q + C1/x-x1 +…+ Ce/x-xe. Замечание: коэф-ты разложения рпавильнойрацион.дроби на сумму простейших дробей находятся методом неопр-х коэф-тов. Для этого, правая часть разложения приводится к общему знаменателю и полученный числитель приравнивается к числителю исходной правильной дроби. Далее, уравниваются коэф-ты при одинаковых степенях x в левой и правой части рав-ва. Приравнивание коэф-тов начинается со степени xна 1 меньше степени знаменателя. В рез-теполучаетсясис-ма линейных ур-ий, кот.имеет единств. реш-е. Это реш-е в общем случае находится методом Гаусса.
51.Первообразная
функция, неопределенный интеграл как
множество первообразных, основные
свойства неопределенных интегралов.
Основная задача ДУ исчисление по
заданной ф-ции, найти ее производную
или диф-л
 основная задача интегр. исчисление
заданной пр-ой восстановить ф-цию. Пусть
ф-ция f(x)определена
на интервале(a,b).Опр1:Первообразной
ф-цией f(x)на
интервале (a,b)
н-ся д-мая ф-ция F(x)для
которой
основная задача интегр. исчисление
заданной пр-ой восстановить ф-цию. Пусть
ф-ция f(x)определена
на интервале(a,b).Опр1:Первообразной
ф-цией f(x)на
интервале (a,b)
н-ся д-мая ф-ция F(x)для
которой
 Т1.(основное
св-во первообразных) Любые 2 первообразные
одной и той же ф-ции отличаются постоянным
слогаемым. Опр2.Совокупность всех
первообразных ф-ции f(x)
на интервале (a,b)н-ся
неопр.интегралом от ф-ции f(x)и
обозначается
Т1.(основное
св-во первообразных) Любые 2 первообразные
одной и той же ф-ции отличаются постоянным
слогаемым. Опр2.Совокупность всех
первообразных ф-ции f(x)
на интервале (a,b)н-ся
неопр.интегралом от ф-ции f(x)и
обозначается ,
а F(x)-какая-либо
первообразная. Ф-ция f(x)
–подынтегральная ф-ция, f(x)dx-подынтегральное
выражение. Интегрирование-многозначная
операция. Осн.св-ва неопр.интегр:1)
,
а F(x)-какая-либо
первообразная. Ф-ция f(x)
–подынтегральная ф-ция, f(x)dx-подынтегральное
выражение. Интегрирование-многозначная
операция. Осн.св-ва неопр.интегр:1) 2)
2) 3)
3) =f(x)+C
4)
=f(x)+C
4) Св-ва
1-4 показывают, что нтегр и диф яв-ся
взаимообратными операциями.5)
Св-ва
1-4 показывают, что нтегр и диф яв-ся
взаимообратными операциями.5)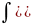 6)
6) 5-6 св-ва линейности неопр интеграла.
5-6 св-ва линейности неопр интеграла.
52.Таблица
простейших интегралов.1) 2)
2) ,
n
,
n
 4)
4) 5)
5)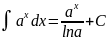
 6)
6) 7)
7) 8)
8) 9)
9) 10)
10) 11)
11) 12)
12) 13)
13) 14)
14) 15)
15) 16)
16) 17)
17)
 18)
18) 19)
19)
53.Основные методы интегрирования: алгебраические и тригонометрические преобразования подынтегральной функции, дифференциальное преобразование подынтегральной функции, замена переменной интегрирования, интегрирование по частям. 1.Непосредственноеинтегриров-е - под знаком интеграла проводим тождественные преобразов-я подинтегральной ф-ии. Используем св-во линейности неопр-го интеграла и таблицу неопр-х интегралов. 2.Интегриров-е подстановкой, замена переменной. Т 1. Пусть ф-ияf(x) непрерывна на отрезке [a,b], а ф-ияx=ϕ(t) нерперывна, имеет непрерывную производную на отрезке [α,β] и при t∈[α,β] x=ϕ(t)∈[a,b].Тогда справедлива фор-ла:∫f(x)dx= ⎸x=ϕ(t) ⎸=∫f(ϕ(t))∙ϕ'(t)dt. ⎸dx=ϕ'(t)dt⎸ Замечания: Эту формулу можно применять как слева направо, так и справа налево. 3.Интегриров-е по частям в неопр-м интеграле. Теорема. Пусть ф-ииU(x) и V(x)име.т непрерывные производные на интервале (a,b), тогда справедлива формула: ∫UdV=U∙V-∫V∙dU (*) Д-во: (UV)'=U'V+UV' (UV)'dx=(U'dx)V+U(V'dx) d(UV)=(dU)V+UdV ∫d(UV)=∫VdU+∫UdV UV=∫VdU+∫UdV ∫UdV=UV-∫VdU, что и треб.док-ть. Замечания: 1.При подборе Uи V интеграл в правой части фор-лы (*) должен быть более простого вида, чем интеграл в левой части этой фор-лы. 2.В кач-веU берём ф-ию, которую трудно интегрировать. 3.Если производная трансцендентной ф-ии снова явл-ся трансцендентной ф-ей, то за U берём алгебраич.ф-ию. 4.Если производная трансцендентной ф-ииявл-сяалгебраич.ф-ей, тогда за U берём трансцендентную ф-ию. Интегриров-е по частям применяется столько раз, какова степень многочлена Pn(x).После применения фор-лыинтегриров-я по частям в правой части получается интеграл, в подынтегральной ф-ии которого надо провести тождественные преобразов-я и получить ур-е относительно исходного интеграла, затем решить это ур-е и найти неопр-ый интеграл.
54.
Интегрирование рациональных дробей.
Рациональной
дробью называется функция R(x),
представленная в виде R(x)= ,
где P(x)
и Q(x)-
многочлены с действительными
коэффициентами. Рациональная дробь
называется правильной, если степень
многочлена в числителе меньше степени
многочлена в знаменателе и неправильной
– в противном случае. Если дробь
неправильная, то разделив числитель
на знаменатель по правилу деления
многочленов, можно представить данную
дробь в виду суммы многочлена на
некоторой правильной дроби. Таким
образом, интегрирование неправильной
дроби сводится к интегрированию
многочлена (что представляет собой
простую задачу) и интегрированию
правильной дроби. Для нахождения
интеграла от правильной рациональной
дроби необходимо в начале разложить
знаменатель дроби на произведение
сомножителей и неприводимых квадратных
трехчленов (дискриминант которых меньше
нуля)
,
где P(x)
и Q(x)-
многочлены с действительными
коэффициентами. Рациональная дробь
называется правильной, если степень
многочлена в числителе меньше степени
многочлена в знаменателе и неправильной
– в противном случае. Если дробь
неправильная, то разделив числитель
на знаменатель по правилу деления
многочленов, можно представить данную
дробь в виду суммы многочлена на
некоторой правильной дроби. Таким
образом, интегрирование неправильной
дроби сводится к интегрированию
многочлена (что представляет собой
простую задачу) и интегрированию
правильной дроби. Для нахождения
интеграла от правильной рациональной
дроби необходимо в начале разложить
знаменатель дроби на произведение
сомножителей и неприводимых квадратных
трехчленов (дискриминант которых меньше
нуля)
55.
Интегрирование тригонометрических
функций.
Интегралы
вида: f(sinx)cosxdx,
f(cosx)sinxdx,
 и
и  dx
находятся методом подведения под знак
дифференциала с использование равенств
d(sinx)=cosxdx;
d(cosx)=sinxdx,
d(tgx)=
dx
находятся методом подведения под знак
дифференциала с использование равенств
d(sinx)=cosxdx;
d(cosx)=sinxdx,
d(tgx)= ;
d(ctgx)=-
;
d(ctgx)=- Универсальная
подстановка Рациональной функцией
R(U,V)
двух переменных U
и V
называется функция, представляющая
собой частное двух многочленов от этих
переменных. Если подынтегральная
функция является рациональной
относительно U=sinx,
V=cosx,
то применяется подстановка tg
Универсальная
подстановка Рациональной функцией
R(U,V)
двух переменных U
и V
называется функция, представляющая
собой частное двух многочленов от этих
переменных. Если подынтегральная
функция является рациональной
относительно U=sinx,
V=cosx,
то применяется подстановка tg =t.
Тогда sinx=
=t.
Тогда sinx= ,
cosx
,
cosx ,
=arctgt
и dx=
,
=arctgt
и dx=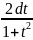 .
Таким образом, интеграл от рациональных
функций по переменным U=sinx
и V=cosx
можно свести к интегралу от рациональной
функции переменной t.
Интегрирование рациональной функции
переменной t
представляет собой задачу об интегрировании
рациональной дроби, которая всегда
решается явно. Следовательно, рассмотренная
подстановка дает возможность найти в
конечном виде (т.е. выразить через
элементарные функции) любой интеграл
R(sinx,cosx)dx.
Именно поэтому она получила название
«универсальной»
.
Таким образом, интеграл от рациональных
функций по переменным U=sinx
и V=cosx
можно свести к интегралу от рациональной
функции переменной t.
Интегрирование рациональной функции
переменной t
представляет собой задачу об интегрировании
рациональной дроби, которая всегда
решается явно. Следовательно, рассмотренная
подстановка дает возможность найти в
конечном виде (т.е. выразить через
элементарные функции) любой интеграл
R(sinx,cosx)dx.
Именно поэтому она получила название
«универсальной»
56.Интегрирование иррациональных функций. Некоторые типы интегралов от алгебраических иррациональностей надлежащей заменой переменных могут быть сведены к интегралам от рациональных функций. Такое преобразование интеграла называется его рационализацией. Для интегрирования рациональной функции , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов: Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение; Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений; Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов; Вычислить интегралы от простейших дробей.
57.Определенный
интеграл, основные свойства, геометрический
смысл.
Определенным интегралом от a
до b
непрерывной функции y=f(x),
определенной на интервале [a;b],
называется прирощение первообразной
F(x)
для этой функции, то есть
 Числа
a
и b
называются нижним и верхним пределом
интегрирования. Основные правила и
свойства определенного интеграла.
Физический смысл определенного
интеграла: Пусть S,
пройденный телом при прямолинейном
движении со скоростью v(t)
за интервал времени от
Числа
a
и b
называются нижним и верхним пределом
интегрирования. Основные правила и
свойства определенного интеграла.
Физический смысл определенного
интеграла: Пусть S,
пройденный телом при прямолинейном
движении со скоростью v(t)
за интервал времени от
 до
до
 вычисляется по формуле S=
вычисляется по формуле S= Геометрический
смысл определенного интеграла: Площадь
S
криволинейной трапеции (фигуры,
ограниченной графиком непрерывной
положительной на интервале [a;b]
функции y=f(x),
осью OX
и прямыми x=a
и x=b)
вычисляется по формуле S=
Геометрический
смысл определенного интеграла: Площадь
S
криволинейной трапеции (фигуры,
ограниченной графиком непрерывной
положительной на интервале [a;b]
функции y=f(x),
осью OX
и прямыми x=a
и x=b)
вычисляется по формуле S=
