74.Признак Лейбница сходимости знакочередующегося ряда.
Знакочередующ.рядом наз-ся ряд любые два соседних членов к-го имеют противоположные знаки.
,где
(5)
Теорема.( Признак Лейбница сходимости знакочередующегося ряда.)
Если
в знакочеред.ряде 5 члены ряда монотонно
убывают по абсолют.величине
и член ряда ,тогда ряд 5 сх-ся и его сумма не превосходит первого члена ряда.
75.Функциональные ряды.Нахождение области сх-ти функционального ряда.
Функциональным рядом наз-ся выражение вида:
(1)
-
общий член ряда
T-обл.опр.ряда
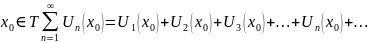(2)-числовой
ряд
Если ряд 2 сх-ся то х0 наз-ся т-ой сходимости функционального ряда1.
Если ряд 2 расх-ся то х0 наз-ся т-ой расходимости функ-ного ряда1.
Областью сх-ти ряда 1 наз-ся совокупность всех точек сх-ти этого ряда.
Областью абсолютной сх-ти функ-ного ряда наз-ся совокупность точек в кот.ряд1 сх-ся абсолютно.
(3)
При каждом конкретном х ряд 3 положительный
При тех х для к-ых Д(х) 1 ряд 3 получается сходящимся значит ряд 1 сх-ся абсолютно.
При тех х к-ых Д(х) ряды 3 и 1 расх-ся.
При тех х для к-ых Д(х)=1 проводится допол.исследование.
76.Степенные ряды.Теорема Абеля.
Степенным рядом называется ряд вида:
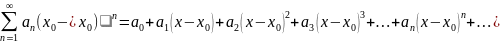(4)
-центр степен.ряда
Теорема Абеля.
Пусть
степен.ряд 4 сх-ся в т.х1 не равной х0
тогда степен. ряд сх-ся при всех
Если степен.ряд 4 расх-ся в т.х2 то он расх-ся для всех
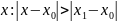
Из теор. Абеля следует что обл.сх-сти степ.ряда есть некоторое мн-во точек симметричных относительно его центра.
77.Радиус и интервал сх-ти степенного ряда.
(4)
Радиусом
сходимости степен.ряда 4 наз-ся число
R
такое что при
ряд
4 сх-ся ,а при
ряд 4 расх-ся.
Замечание.
При R=0степ.ряда 4 сх-ся только в точке -в центре.
При
R=
степен.ряд 4 сх-ся на всей числовой оси
Ф-лы для нахождения радиуса сх-ти степен.ряд.
R=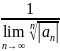
Интервалом
(х0-R,x0+R)наз-ся интервалом сх-ти степ.ряда
4 на этом интервале ряд4 сх-ся абсолютно,а
на интервале (
,х0-R)
и
степ.ряд расх-ся.
На концах интервала сх-ти в точках х0+R и х0-R проводится дополн.исследование степ.ряда.
Значение х0-R,х0+R подставляются вместо х в степен.ряд 4 при этом получаются числовые ряды и исследуется их сходимости.
78.Дифференцирование и интегрирование степенных рядов.
Теорема
Внутри интервала сх-ти степен.ряд можно по численно
дифф-вать и по численно интегрировать при этом радиус сх-ти ряда не меняется.
Сх-ть
ряда может изменится только на концах
интервала сходимости в точках
80.Ряды Маклорена и Тейилора.Разложение элементарных ф-ций в степенные ряды. Пусть f(x) имеет непрерывные производные до n+1-го порядка включительно в окр-ти т.x0. Тогда, f(x) можно представить в виде: f(x)=f(x0)+f'(x0)∙(x-x0)+f''(x0)/2! ∙(x-x0)2+f'''(x0)/3! ∙(x-x0)3+…+f(n)(x0)/n! ∙(x-x0)n+Rn(x). (3), где Rn(x)-остаточный член формулы Тейлора. Формула Тейлора (6) позволяет произвольную ф-июf(x) представить в виде суммы многочлена и остатка. Rn(x)=f(n+1)(Θ)/(n+1)! (x-x0)n+1 – ост.член в фор-ле Лагранжа. Θ∈(x0,x). Ряд Тейлора. Пусть f(x) имеет непрерывные производные любого порядка в окр-ти т.x0. Тогда f(x) можно поставить в соответствие ряд: f(x)~f(x0)+f'(x0)(x-x0)+f''(x0)/2! (x-x0)2 + f'''(x0)/3!(x-x0)3+…+f(n)(x0)/n! (x-x0)n+… (7) Ряд (7) наз-ся рядом Тейлора для ф-ииf(x). Если x0=0, то получим ряд Макларена. f(0)+f'(0)x+f''(0)/2! ∙x2 + f'''(0)/3! ∙x3+…+f(n)(0)/n! ∙xn+… (8) Опр.1-если f(x) бесконечно диф-ма в окр-ти т.x0 и формально составленный степенной ряд (7) для этой ф-ии сходится, и сумма ряда=f(x), то говорят, что f(x) разлагается в степенной ряд и: f(x)=f(x0)+f'(x0)(x-x0) + f''(x0)/2! ∙(x-x0)2 + f'''(x0)/3! ∙(x-x0)3+…+f(n)(x0)/n! ∙(x-x0)n +… Теорема 1. Если f(x) разлагается в ряд Тейлора, то это разложение единственное. Теорема 2 (н. и д. усл-е разложения ф-ии в степенной ряд). Для того, чтобы f(x) разлагалась в ряд Тейлора, н. и д., чтобы f(x)была бесконечно диф-ма в окр-ти т.x0и чтобы в фор-ле (6) limRn(x)=0. n→∞ Теорема 3 (достаточ.Усл-е разложения ф-ии в степенной ряд). Пусть f(x) бесконечно диф-ма в окр-ти т. x0 [x0-h,x0+h] и все её производные ограничены в этой окр-ти конечным числом, ⎸f(n) (x)⎸≤M. ∀x∈[x0-h,x0+h] ∀n=1,2,3,4,… тогда f(x) разлагается в ряд Тейлора