II. Перевод правильной десятичной дроби в двоичную, восьмеричную и шестнадцатеричную сс

Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения.

Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

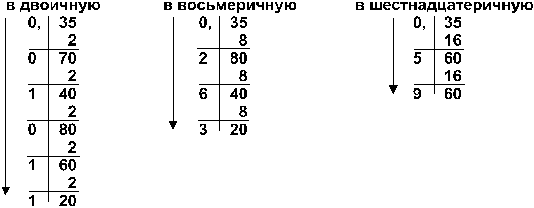
Ответ: 0,35₁₀ = 0,01011₂ = 0,263₈ = 0,59₁₆ .

Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае, пеpевод осуществляется до заданной точности. Достаточно того количества цифp в pезультате, котоpое поместится в ячейку.

Задание. Перевести число 0,715 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную.

Ответ: 0,715₁₀ = 0,10110₂ = 0,556₈ = 0,B7₁₆

III. Перевод чисел из двоичной, восьмеричной, шестнадцатеричной системы в десятичную

При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Примеpы:

Задание. Сделать следующий перевод:

101101₂ = Х₁₀. Ответ: 101101₂ = 45₁₀;

55₈ = Х₁₀. Ответ: 55₈ = 45₁₀;

2D₁₆ = X₁₀. Ответ: 2D₁₆= 45₁₀.

IV. Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную?

Следует иметь в виду, что основание восьмеричной системы счисление 8 = 2³ – является целой степенью числа 2, поэтому для перевода достаточно каждый восьмеричный разряд представить тремя двоичными (триады).

Основание шестнадцатеричной системы счисление 16 = 2⁴ – тоже является целой степенью числа 2, поэтому для перевода достаточно каждый шестнадцатеричный разряд представить четырьмя двоичными (тетрады).

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

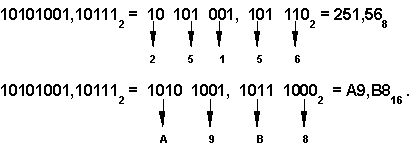
Задание. Сделать следующий перевод:

101101₂ = Х₈. Ответ: 101101₂ = 55₈.

101101₂ = Х₁₆. Ответ: 101101₂ = 2D_16.

Для упрощения перевода можно заранее подготовить таблицы (см. Табл. 2 и Табл. 3 ниже).

V. Перевод чисел из восьмеричной и шестнадцатеричной системы в двоичную

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (группы по 3 цифры) в восьмеричные цифры:

Таблица 2.

Двоичные триады	000	001	010	011	100	101	110	111
Восьмеричные цифры	0	1	2	3	4	5	6	7

Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных тетрад (группы по 4 цифры) в шестнадцатеричные цифры:

Таблица 3.

Двоичные тетрады	0000	0001	0010	0011	0100	0101	0110	0111
Шестнадцатеричные цифры	0	1	2	3	4	5	6	7
Двоичные тетрады	1000	1001	1010	1011	1100	1101	1110	1111
Шестнадцатеричные цифры	8	9	10 A	11 B	12 C	13 D	14 E	15 F

Задание. Перевести в двоичную систему счисления следующие числа:

46,27₈ = X₂. Ответ: 46,27₈ = 100110,010111₂.

EF,12₁₆ = X₂. Ответ: EF,12₁₆ = 11101111,0001001₂.

Сводная таблица переводов целых чисел из одной системы счисления в другую

Рассмотрим только те системы счисления, которые применяются в компьютерах — десятичную, двоичную, восьмеричную и шестнадцатеричную.

Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую.

Порядок переводов определим в соответствии с рисунком 1:

Рисунок 1

На этом рисунке использованы следующие обозначения:

• в кружках записаны основания систем счисления;

• стрелки указывают направление перевода;

• номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице 3.

Например: означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.