20.Синусоидальный ток в емкости (фазовый сдвиг; емкостное сопротивление и проводимость, волновая и векторные диаграммы, энергия электрического поля, реактивная мощность).

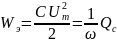Величина ,имеющая размерность сопротивления, назыв. емкостным сопротивлением. Обратная ей величина назыв. емкостной проводимостью. Разность фаз двух синусоидальных сигналов одной частоты y₁ – y₂ = 0 называется их фазовым сдвигом. Энергия электрического поля .Реактивная мощность - величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению действующих значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: .

Векторная и волновая диаграммы:

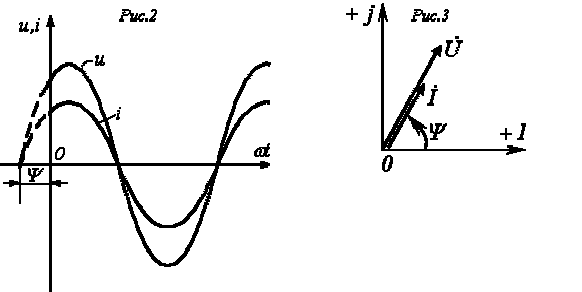
23 Мощность цепи синусоидального тока. Комплексная, полная, активная и реактивная мощности. Треугольник мощностей. Коэффициент мощности.

АКТИВНАЯ, РЕАКТИВНАЯ И ПОЛНАЯ МОЩНОСТИ ЦЕПИ

Умножив стороны треугольников напряжений на ток I, получим треугольники мощностей. Стороны треугольников мощностей соответственно означают:

Р = U_rI = I²r — активная мощность цепи, Вт, кВт

Q_L = U_LI = I²x_L —реактивная индуктивная мощность цепи, обусловленная энергией магнитного поля, вар, квар

Q_С = U_СI = I²х_С — реактивная емкостная мощность цепи, обусловленная энергией электрического поля, вар, квар

Q = Q_L - Q_С = I²x — реактивная мощность цепи, вар, квар, это та мощность, которой приемник обменивается с сетью;

S = UI = I²z — полная мощность цепи. В • А, кВ • А

cos φ = r/z = P/S—коэффициент мощности цепи Коэффициентом мощности, или «косинусом фи» цепи называется отношение активной мощности к полной мощности

Из треугольников мощностей можно установить следующие связи между Р, Q, S и cos φ:

P = S cos φ = UI cos φ;

Q = S sin φ = UI sin φ;

S = √P² + Q² = UI .

За единицу активной мощности принят ватт (Вт) или киловатт (кВт), реактивной мощности — вольтампер реактивный (вар) или киловольтампер реактивный (квар), полной мощности — вольтампер (ВА) или киловольтампер (кВ•А).

Реактивные (индуктивная, емкостная) мощности, обусловленные соответственно энергией магнитного поля индуктивности и электрического поля емкости, не совершают никакой полезной paботы, однако они оказывают существенное влияние на режим работы электрической цепи. Циркулируя по проводам трансформаторов, генераторов, двигателей, линий передач, они нагревают их. Поэтому расчет проводов и других элементов устройств переменного тока производят, исходя из полной мощности S, которая учитывает активную и реактивную мощности.

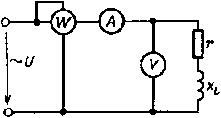
Рис. 2.13. Схема включения приборов для измерения активной, реактивной и полной мощностей

цепи, а также ее параметров

Коэффициент мощности имеет большое практическое значение: он показывает, какая часть полной мощности является активной мощностью. Полная мощность и коэффициент мощности наряду с другими параметрами являются расчетными величинами и в конечном счете определяют габаритные размеры трансформаторов, генераторов, двигателей и других электротехнических устройств.

Измерение активной, реактивной, полной мощностей и cos φ, а также параметров цепи, например r и L, можно произвести с помощью ваттметра, амперметра и вольтметра, включенных в цепь по схеме, изображенной на

Ваттметр измеряет активную мощность Р цепи. Полная мощность цепи равна произведению показаний вольтметра и амперметра.

Реактивную (индуктивную) мощность и коэффициент мощности цепи (рис. 2.13) определяют расчетным путем по формулам Q = √S² - Р², cos φ = P/S.

Активное сопротивление находят из формулы

Р = I²r, откуда r = P/I². Полное сопротивление цепи

z = U/I. Индуктивное сопротивление xL = √z² - r².

Индуктивность L определяют из формулы x_L = 2πfL,

откуда L=x_L/2πf.

ТРЕУГОЛЬНИК МОЩНОСТЕЙ - графическое изображение активной, реактивной и полной мощностей в цепи переменного тока.

Треугольник мощностей получается из соотношения Р² + Q² = S²