53. Квазистационарные токи. Свободные колебания в контуре без активного сопротивления.

Переменный ток квазистац. тока в каждый момент времени сила тока находится во внешних проводниках. Переменный ток в цепи, для которой выполняется соотношение t<<T и для которой с высокой точностью можно пользоваться законами постоянного тока, называется квазистационарным током.

Условия существования тока:

1)время передачи возмущений с эл цепи на расстоянии намного меньше периода индуктивности тока

2)

Колебания в контуре можно вызвать вызвав индуктивности ток (например включив магнитное поле).

Поскольку активное сопротивление контура , полная энергия остаётся постоянной. Если энергия конденсатора равна нулю, то энергия магнитного поля максимальна, и наоборот.

Энергия электрического поля аналогична потенциальной энергии mgh или 1/2kx2, а энергия магнитного поля аналогична кинетической энергии ; L играет роль массы т, 1/С – роль коэффициента жесткости k. Наконец, заряду q соответствует смещение маятника из положения равновесия х, силе тока I – скорость υ, а напряжению U – ускорение а.

В соответствии со вторым законом Кирхгофа (и законом сохранения энергии), можно записать: т.к. тогда получим

Введем обозначение: – собственная частота контура, отсюда получим основное уравнение колебаний в контуре: Решением этого уравнения является выражение вида

Таким образом, заряд на обкладке конденсатора изменяется по гармоническому закону с собственной частотой контура ω0. Для периода колебаний справедлива формула Томсона:

Продифференцируем по времени и получим выражение для тока:

Напряжение на конденсаторе отличается от заряда на 1/С:

Таким образом, ток опережает по фазе напряжение на конденсаторе на π/2. На индуктивности, наоборот, напряжение опережает ток на π/2. где – волновое сопротивление [Ом]. Это закон Ома для колебательного контура.

54. Свободные затухающие колебания. Логарифмический декремент затухания. Добротность.

Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего колебания затухают. ;

отсюда,

- уравнение затухающих колебаний в контуре с R, L и С;

- коэффициент затухания;

Диф ур затухающих колебаний Решение

Добротность контура

Характеризует качество колебательного контура. Численно равна отношению напряжения на любом из реактивных участков на резонансе к напряжению, подводимому к контуру, или отношению реактивного сопротивления к активному.

где f-частота колебаний, W-энергия, запасенная в колебательной системе, Pd-рассеиваемая мощность

Логарифмическим декрементом затухания

Это - величина, показывающая скорость затухания собственных колебаний и определяемая как натуральный логарифм отношения следующих друг за другом амплитуд колебаний

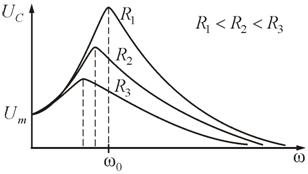
55. Вынужденные электромагнитные колебания. Резонансные кривые

Вынужденными электромагнитными колебаниями называют периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника.

При равномерном вращении рамки вокруг оси с угловой скоростью w магнитный поток, пронизывающий рамку, будет изменяться с течением времени по закону:

Изменение магнитного потока возбуждает в рамке ЭДС индукцию, равную

где Е0= ВSw - амплитуда ЭДС.

Резонансными кривыми называются зависимости тока и напряжения от частоты Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению:

Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением

Д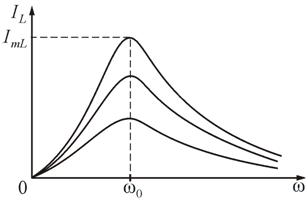 ля напряжения Для силы тока