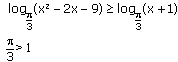Логарифмическая функция

Функция вида   y = log_a х (где а > 0, а ≠ 1)   называется логарифмической.

1) Область определения логарифмической функции — множество всех положительных чисел. Это следует из определения логарифма, так как выражение log_ax имеет смысл только при x > 0.

2) Множество значений логарифмической функции — множество R всех действительных чисел. Это следует из того, что для любого действительного числа b есть такое положительное число x, что log_ax = b, т.е. уравнение log_ax = b имеет корень. Такой корень существует и равен x = a^b, так как log_aa^b = b.

3) Логарифмическая функция y = log_ax является возрастающей на промежутке x > 0, если a > 0, и убывающей, если 0 < a < 1.

4) Если a > 0, то функция y = log_ax принимает положительные значения при x > 1,отрицательные — при 0 < x < 1. Если 0 < a < 1, то функция y = log_ax принимает положительные значения при 0 < x < 1, отрицательные — при x > 1. Это следует из того, что функция y = log_ax принимает значение , равное нулю, при x = 1 и является возрастающей на промежутке x > 0, если a > 1, и убывающей, если 0 > a > 1.

Ниже представлены графики логарифмических функций при a > 0 (1);   0 > a >1 (2).

Стоит отметить, что график любой логарифмической функции y = log_ax проходит через точку (1 ; 0)

35. Формулы и свойства логарифмов

Логарифм числа b по основанию a (log_ab) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует только у положительных чисел).

Обозначение: log_ab.

log_ab = x, a^x = b.

Логарифм числа b по основанию a - log_ab (a > 0, a ≠ 1, b > 0)

Десятичный логарифм - lg b (Логарифм по основанию 10, а = 10).

Натуральный логарифм - ln b (Логарифм по основанию e, а = e).

Формулы и свойства логарифмов

1°    Основное логарифмическое тождество - a^log_a^b = b;

2°    log_a1 = 0;

3°    log_aa = 1;

4°    log_a(bc) = log_ab + log_ac;

5°    log_a(b/c) = log_ab - log_ac;

6°    log_a(1/c) = log_a1 - log_ac = - log_ac;

7°    log_a(b^c) = c log_ab;

8°    log_(a^c₎b = (1/c) log_ab;

9°    Формула перехода к новому основанию - log_ab = (log_cb)/(log_ca);

10°    log_ab = 1/log_ba;

Переход от выражения к логарифму называется логарифмированием этого выражения. Переход от логарифма к подлогарифмическому выражению называется потенциированием. В математике преимущественно используют натуральные логарифмы. Свойства и формулы логарифмов незаменимы при решении логарифмических уравнений и функций, упрощении примеров, также они пригодятся при решении интегралов и нахождении производной от логарифмов.

36. Основными методами решения логарифмических уравнений являются следующие:

• равносильные преобразования;

• переход к уравнению-следствию;

• замена переменной;

• разложение на множители.

Логарифмические уравнения — это уравнения, содержащие неизвестное под знаком логарифма и (или) в его основании.

Простейшим логарифмическим уравнением является уравнение вида log_ax = b, где a и b — данные числа,x — неизвестное.

Уравнение имеет решение, если a > 0, a ≠ 1: x = a^b

При решении логарифмических уравнений и неравенств пользуются свойствами логарифмов, а также свойствами логарифмической функции

y=log_ax, a > 0, a  1:

1) Область определения:  x > 0;

2) Область значений:  y R;

3)  log_ax₁=log_ax₂ x₁=x₂;

4) При a>1 функция y=log_ax возрастает, при 0 < a < 1 функция y=log_ax убывает при всех x > 0, т.е.

a >1  и log_ax₁>log_ax₂ x₁>x₂,

0 < a < 1 и log_ax₁>log_ax₂ x₁ < x₂;

При переходах от логарифмических уравнений (неравенств) к уравнениям (неравенствам), не содержащим знака логарифма, следует учитывать область допустимых значений (ОДЗ) исходного уравнения (неравенства).

Решение логарифмических неравенств основано на монотонности логарифмической функции. При решении логарифмических неравенств, нахождение области допустимых значений (О.Д.З.) заданного неравенства в большинстве случаев является нецелесообразным. Обычно условия, задающие О.Д.З. неравенства, подключают к тому неравенству, которое является следствием заданного неравенства, и решают затем полученную систему. Можно также использовать метод интервалов.

 Примеры.

 Решить неравенство:

а) log₃ (х + 2) < 3

Решение:

D (log_а) =R₊,

следовательно х + 2 > 0.

Функция y=log₂t возрастающая, следовательно, 0 < х + 2 < 27, -2< х < 25.

Ответ: (-2; 25)

б)

следовательно, функция

возрастает на промежутке

(0; + ).

Данное неравенство равносильно системе:

Неравенство х² – 3х – 10≥ 0 решим методом интервалов

х₁ = 5 ; х₂ = –2 (х – 5)(х + 2) ≥ 0

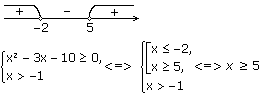
Ответ: [5; + ).

Логарифмические неравенства отличаются от уравнений тем, что результатом будет одно-два конкретных значения, а интервал значений. Приемы решений – те же самые.

Важно помнить, что если основание логарифма больше 1, то данная логарифмическая функция – возрастающая, и под логарифмические выражения таких функций соотносятся между собой так же, как и эти функции (знак неравенства сохраняется). Если же основания логарифмов меньше 1, то под логарифмические выражения соотносятся между собой обратно тому, как соотносятся сами функции (знак неравенства меняется на противоположный).

.