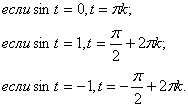Теорема. Если a и b — катеты, c — гипотенуза прямоугольного треугольника abc, то выполняются следующие равенства:

20. Графики функций y=sin x; y=cos x и их свойства.

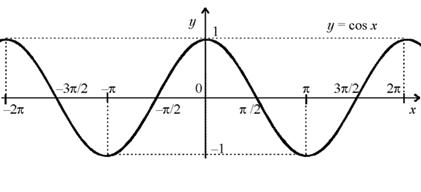
а)  Область определения:   D (cos x) = R .

    б)  Множество значений:   E (cos x ) = [ – 1 ,  1 ] . в)  Четность, нечетность:   функция четная.

    г)  Периодичность:   функция периодическая с основным периодом  T = 2 .

д)  Нули функции:  cos x = 0  при   x =   +  n,   n   Z.

.      ж)  Промежутки монотонности:

;

.

      з)  Экстремумы:

;             .

Функция ограничена с низу и сверху.

Непрерывна

     График функции    y= cos x   изображен на рисунке.

 

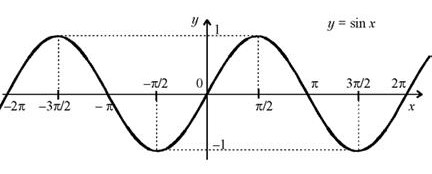
а)  Область определения:   D (sin x) = R .

    б)  Множество значений:   E (sin x) = [ – 1 ,  1 ] . в)  Четность, нечетность:   функция нечетная.

    г)  Периодичность:   функция периодическая с основным периодом  T = 2 .

    д)  Нули функции:  sin x = 0  при   x =  n,   n   Z.

   

      ж)  Промежутки монотонности: ;

.

      з)  Экстремумы:  ;           .

     График функции    y= sin x   изображен на рисунке.

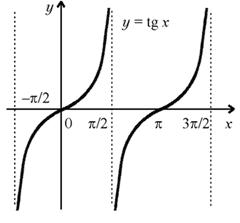
21. а)  Область определения:   D (tg x) = R \ { /2 +   n( n   Z ) }.

    б)  Множество значений:   E (tg x ) = R . в)  Четность, нечетность:   функция нечетная.

    г)  Периодичность:   функция периодическая с основным периодом  T =  .

    д)  Нули функции:  tg x = 0  при   x =  n,   n   Z(целые числа).

      е)  возрастает и не прерывна на интервале ( ,

ж) не ограничена ни сверху ни снизу

з) Нет мак и нет минима

;        .

      ж)  Промежутки монотонности:  функция возрастает на каждом интервале, целиком принадлежащем ее области определения.

      з)  Экстремумы:  нет.

   График функции   y = tg x   изображен на рисунке.

 а)  Область определения:   D (ctg x) = R \ {  n( n   Z ) }.

    б)  Множество значений:   E (ctg x ) = R . в)  Четность, нечетность:   функция нечетная.

    г)  Периодичность:   функция периодическая с основным периодом  T =  .

    д)  Нули функции:  ctg x = 0  при   x =  /2 +  n,   n   Z.

    е)  Промежутки знакопостоянства ; ;        .

     ж)  Промежутки монотонности:  функция убывает на каждом интервале, целиком принадлежащем ее области  определения.

     з)  Экстремумы:  нет.

   График функции   y = ctg x  изображен на рисунке.

 

22. Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.

Уравнения вида sin x = a; cos x = a; tg x = a; ctg x = a, где x - переменная, a R, называютсяпростейшими тригонометрическими уравнениями.

 

Методы решения тригонометрических уравнений. Решение тригонометрического уравнения состоит из двух этапов:  преобразование уравнениядля получения его простейшего вида ( см. выше ) и  решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения  тригонометрических уравнений.

 

1. Алгебраический метод.  Этот метод нам хорошо известен из алгебры

   ( метод замены переменной и подстановки ).

2. Разложение на множители.  Этот метод рассмотрим на примерах.

3.Приведение к однородному уравнению. Уравнение называется однородным относительно  sin  и  cos, если все его члены одной и той же степениотносительно sin  и cos  одного и того же угла. Чтобы решить однородное уравнение, надо:      а)  перенести все его члены в левую часть;    б)  вынести все общие множители за скобки;    в)  приравнять все множители и скобки нулю;    г)  скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на          cos ( или sin ) в старшей степени;     д)  решить полученное алгебраическое уравнение относительно tan .

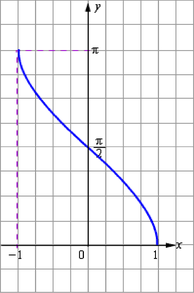
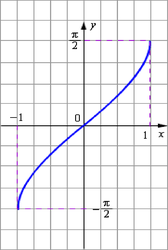
• Y=arcsin x-это функция, обратная к функции y=sin x, x ( , то функия, обратная синусу. То есть, её аргументом является значение синуса исходного угла, а возвращает она исходный угол. 

Свойства:

D(f)=(-1;1)

Е(f)= (

Нечетная

Возрастает

Непрерывна

• 

Функция   непрерывна и ограничена.

Функция   является строго убывающей

 (область определения),

 (область значений).

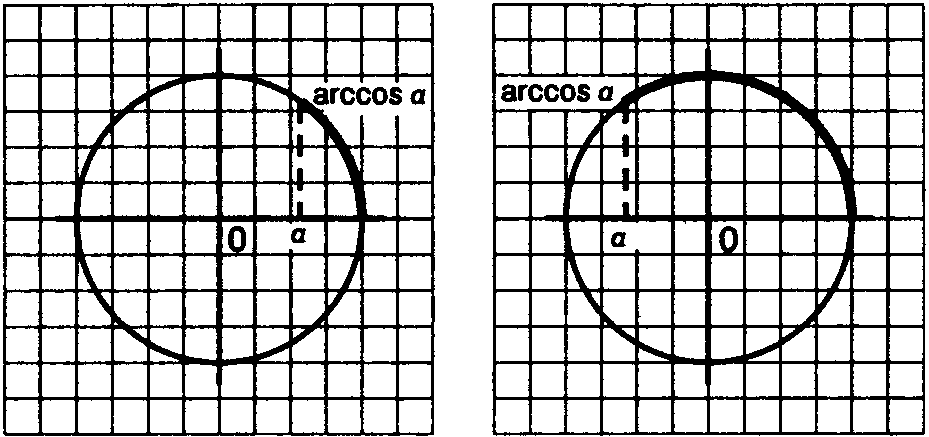
Арккосинус (от лат. arcus — дуга и косинус), одна из обратных тригонометрических функций.

Y=arcos x обратная функция y=cos x, x (o;п)

Свойства:

D(f)=(-1;1)

Е(f)= (o;п)

Не четная и не нечетная .

Убывает

Непрерывна

Определение. Если |a|≤1, то arccos a (арккосинус a) — это такое число, из отрезка [0; π], косинус которого равен a.

Арккосинус. Решение уравнения cos t=α

Определение. Если |a|≤1, то arccos a (арккосинус a) — это такое число, из отрезка [0; π], косинус которого равен a.

Теперь можно сделать общий вывод о решении уравнения cost = a:

Если |a|≤1, то уравнение cost = a имеет решения:

Правда, в трех случаях предпочитают пользоваться не полученной общей формулой, а более простыми соотношениями:

Арктангенс и арккотангенс. Решение уравнений tg x=α Определение 1. arctg a (арктангенс a) — это такое число, из интервала  , тангенс которого равен a. Общее решение уравнения tg x = а имеет вид: Для любого значения a справделива формула: arcctg a (арккотангенс a) — это такое число, из интервала , котангенс которого равен a. Общее решение уравнения ctg x = а имеет вид: Для любого допустимого значения a справделива формула:

Уравнение ctg x = а практически всегда можно преобразовать к виду  .

24. Определение. Уравнения вида asinx + bcosx=0 называют однородными тригонометрическими уравнениями первой степени; уравнения вида asin²+ bcosxsinx+ ccos²x =0 называют однородными тригонометрическими уравнениями второй степени.

Алгоритм решения уравнения asin²+ bcosxsinx+ ccos²x =0

1. Посмотреть, есть ли в уравнении член asin²х.

2. Если этот член содержится, то уравнение решается делением обеих его частей на cos²x и последующем введением новой переменной z=tgx.

3. Если asin²х не содержится, то уравнение решается методом вынесения общего множителя за скобки.

 Существует два метода решения тригонометрических уранений: разложение на множители и введение новой переменной.

26. Для преобразования тригонометрических выражений используют свойства тригонометрических функций и тригонометрические формулы указанные ниже.  Формулы суммы и разности синуса и косинуса справедливы для любых 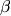 ,  а формулы суммы и разности тангенса верна при  + − , отличных от + 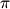k k Z. 

28. Здесь речь пойдет о формулах тригонометрии, позволяющих выразить 

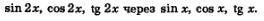
• В формулах синуса и косинуса суммы двух углов  sin( + )=sin cos +cos sin ,  cos( + )=cos cos −sin sin   заменим   на  , получим соотношения:

sin( + )=sin( + )=sin cos +cos sin sin2 =2sin cos ;

cos( + )=cos( + )=cos cos −sin sin cos2 =cos2 −sin2 .

Если подставить формулы sin2 =1−cos2 , cos2 =1−sin2  в последнем соотношении,  то получим еще две формулы косинуса двойного угла: cos2 =1−2sin2  и cos2 =2cos2 −1.

В формуле тангенса суммы двух углов tg( + )=tg +tg 1−tg tg   заменим   на  , получим соотношение.

Итак, получили следующие формулы: 

Формулы «синус двойного аргумента» и «косинус двойного аргумента» справедливы для любых значений аргумента (никаких ограничений нет), тогда как формула «тангенс двойного аргумента» справедлива лишь для тех значений аргумента х, для которых определены tg х и tg 2 х, а также отличен от нуля знаменатель дроби, т.е.  Разумеется, формулы двойного аргумента можно применять и в тех случаях, когда место аргумента х занимает более сложное выражение. Так, справедливы следующие соотношения:

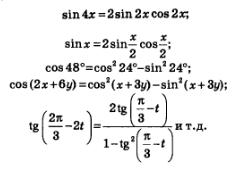
• Так называются формулы, позволяющие перейти от степеней тригонометрических функций к функциям в первой степени, но от кратного аргумента:

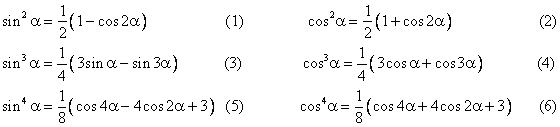
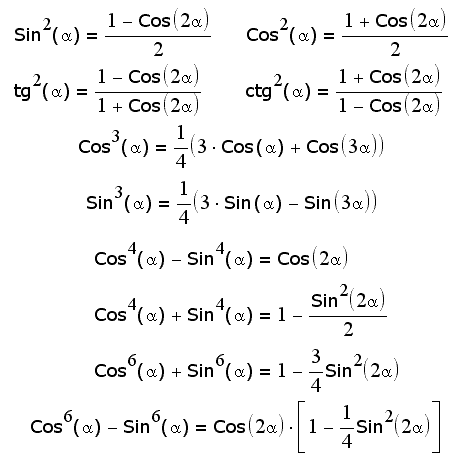
29. Рассмотрим формулу 2sinXcosY=sin(X+Y)+sin(X-Y)

Обозначим в правой части этой формулы X+Y через  , а X-Y через  .  Складывая и вычитая равенства X+Y=   и X-Y=  ,  находим, что X=2 + , Y=2 −   подставляя эти выражения в левую часть формулы и читая формулу справа налево, получаем окончательно:  sin +sin =2sin2 + cos2 −

Подставляя в только что полученную формулу -   вместо  ,  получаем sin −sin =2sin2 − cos2 + .

Аналогично можно вывести все остальные формулы

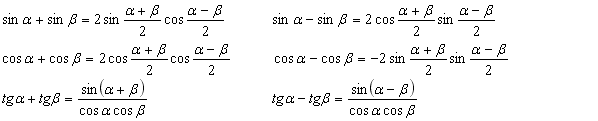
Теорема. Для любых   и   справедливы равенства

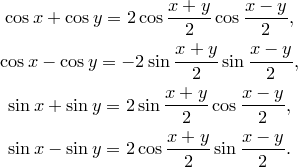
Доказательство. Все четыре формулы доказываются преобразованием правой части в сумму

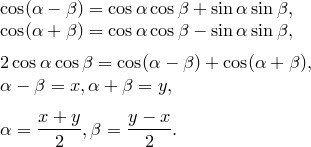
30. Показательная функция, такая функция, которая может быть задана формулой 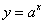 , где а - любое положительное число, не равное единице.