Применение условий однозначности для цилиндра с бесконечной высотой

Запишем решение уравнения реактора:

Рассмотрим условия однозначности:

1. Условие неотрицательности и ограничения нейтронного потока:

Ф(r, z) ≥ 0

во всём диапазоне от 0 до l, от 0 до Н/2:

0≤ r≤ R_аз 0≤ z≤ Н_аз / 2

Из этого условия следует, что .

2. Рассмотрим граничное условие (рис.13):

3. Условие неотрицательности нейтронного потока (рис.14):

Из этого условия следует, что , т.к. при больших значениях произведения Ф может принимать отрицательные значения.

Полученное равенство называется условием критичности реактора, из этого условия найдём:

1. К_эф :

;

где , - геометрический параметр.

т.е. в критическом реакторе геометрический и материальный параметры равны.

2. R_аз:

3. Ф(r):

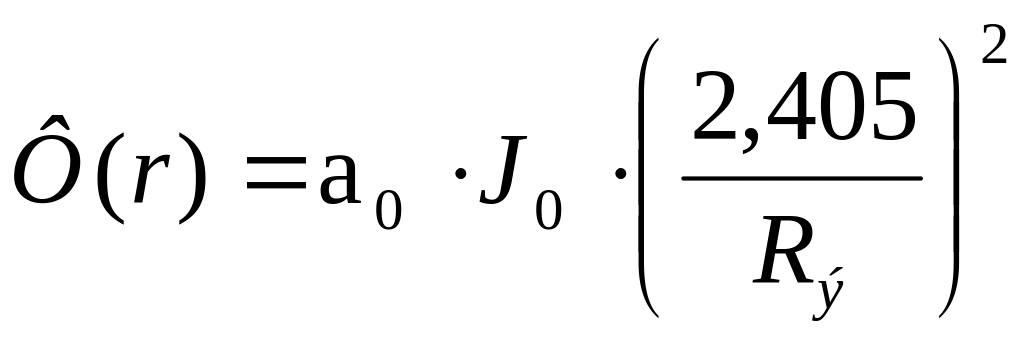
В результате решения задачи и применения к этому решению условия однозначности вытекают 3 способа достижения критичности реактора:

1. Изменение материального параметра, т.е. состава активной зоны.

– условие критичности

2. Изменение размеров активной зоны (радиуса и высоты).

3.Изменение и материального параметра и размеров активной зоны.

Также, если форма активной зоны не фиксирована, то критичность может достигаться изменением геометрии активной зоны.

Например:

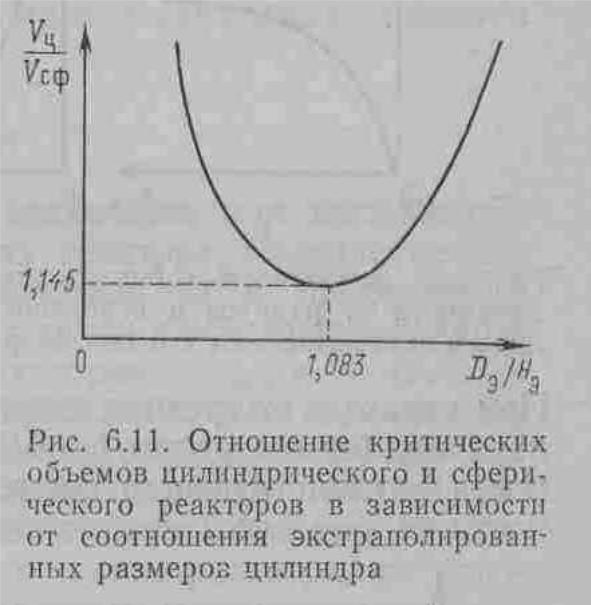
Рис.15. Отношение критических объемов цилидрического и сферического реактора в зависимости от соотношения экстраполированных размеров цилиндра

Из рис.15 следует, что объём цилиндра (цилиндрической активной зоны) критический зависит от соотношения диаметра и высоты.

Применение условия однозначности для цилиндра с бесконечным радиусом

Запишем решение уравнения реактора:

Рассмотрим условия однозначности:

1. Условие симметрии нейтронного потока:

Ф' (z) _z=0 = 0 этому условию не удовлетворяет функция , поэтому имеем:

Начало координат в центре активной зоны.

2. Граничные условия:

Ф (Н_э) = 0

где , .

3.Условие неотрицательности нейтронного потока:

т.к. при , Ф принимает отрицательные значения. Поэтому получим условие критичности:

Решение уравнения реактора для цилиндрической активной зоны с конечными радиусом и высотой активной зоны

Запишем уравнение реактора:

Для решения воспользуемся методом разделения переменных, согласно которому:

Ф(r, z) = Ф(r) · Ф(z)

С учётом этого запишем уравнение реактора:

Чтобы решить уравнение необходимо по отдельности найти Ф(r) и Ф(z), а для этого следует рассмотреть 2 задачи: радиальную, чтобы найти Ф(r) и высотную, чтобы найти Ф(z).

Двухгрупповое уравнение реактора

В двухгрупповой теории считают, что все нейтроны сгруппированы в 2 группы (рис.17). При этом часть нейтронов входит во 2 группу:

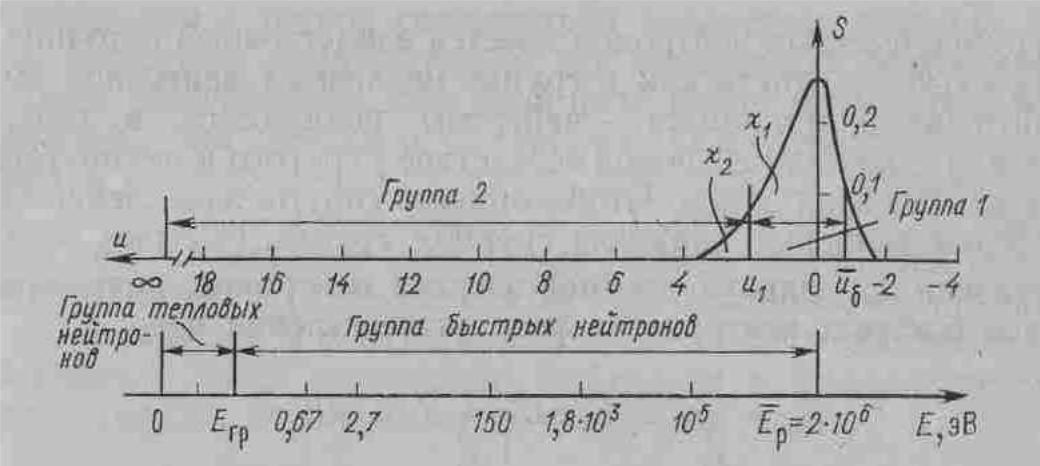
Рис.17. Энергетические границы двухгрупповой модели при произвольном (вверху) и тепловом (внизу) спектрах

S(Е) – спектр нейтронов деления (Кронберга).

Спектр замедляющихся нейтронов описывается спектром Ферми, а тепловых – спектром Максвелла. Обозначим источник нейтронов через Q:

где индекс I – относится к нейтронам I группы, а индекс II – ко II группе нейтронов.

Если общее число нейтронов деления принять за единицу, то: .

Дифференциальная кривая – число нейтронов, приходящихся на единицу энергии. Т.е. энергетический спектр нейтронов деления пронормирован на единицу (рис.17).

Обозначим долю нейтронов деления I группы через , тогда долю нейтронов второй группы: .

Средневзвешенная энергия деления нейтронов равна:

2 МэВ

Двухгрупповое уравнение представляет собой систему 2 уравнений, каждое из которого – баланс нейтронов в данной группе. Рассмотрим источники генерации и источники убыли нейтронов для каждой группы(табл.2):