15. Динамическое программирование. Построение решения.
Рассматривается подход к решению специальных классов задач, которые имеют характер процессов многошаговых, многоэтапных, развивающихся во времени (динамических).
Общая схема метода динамического программирования
Метод, как правило, включает 3 этапа:
I этап: инвариантное погружение. ; II этап: строится уравнение Беллмана для этой функции. ; III этап: заключается в решении уравнения Беллмана и построению по этому решению оптимального плана исходной задачи.
Решение уравнения (6) и (7)
Уравнение (6) будем
решать последовательно, положим в (6)
,
тогда получим
.
Справа под максимумом стоит известная
функция, решая задачу максимизации,
найдём
.
На 2-ом шаге полагаем
в (6)
,
аналогично находим
и так далее. Пройдя последовательно
шаг, мы построим полное решение уравнения
Беллмана:
.
Приступаем к построению оптимального плана задачи
; ; .
Полагаем в ф-ции
Беллмана
тогда, очевидно,
будет искомая максимальная прибыль.
Одновременно мы найдём
.
Эта оптимальная компонента для
-го
ресурса, тогда для процессов
остаток ресурса будет
и найдём, что
и т.д. Для любого
:
.
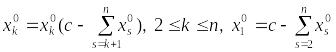Задача решена полностью.
Метод динамического программир-ния имеет свои преимущества и недостатки.
Преимущества:
задача оптимизации с переменными сводится к задачи одномерной оптимизации.
результатом метода динамического программир-ния явл. всегда оптимал. план, а не локально оптимальные планы как в большинстве других планов.
результаты решённой задачи оптимизации можно использовать в случае изменения параметров
зад. одномерной оптимизации реш. методом поиска, поэтому метод динамич. программир-ния может использоваться для задачи оптимизации, в кот. ф-ции не являются дифференциальными, непрерывными, аналитическими.