5. Минимизация унимодальных функций. Равномерный перебор.
Рассм. задачу , (1) где – некоторые числа ( ).
Методы минимизации
унимодал. ф-ций. Опр.
Ф-ция
наз. унимодальной
на [
],
если сущ.точка
т, что на
ф-ция
монотонно убывает, а на
монотонно возрастает.
-
оптимал. план задачи (1).
В зад.(1)унимодальная
ф-ция имеет единств. оптимал. план и не
имеет локал. минимумов. Если в задаче
(1)
(3)
,
то ф-ция строго выпукла и явл. унимодальной.
Если в зад.(1) ф-ция
не унимодальная, то в некоторых случаях
[a,b]
с помощью нерав-ва (3) её удаётся разбить
на интервалы унимодальности, затем
чтобы реш. исходную зад.(1) достаточ. на
каждом таком отрезке реш. задачу
минимизации унимодал. ф-ции и простым
перебором найти оптимал. план.
Будем решать задачу (1), в которой - унимодальная функция.
Поставим цель: по
заданному
найти на [a,b]
такую часть
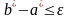(длиною
)
и чтобы
.
Эта задача называется задачей локализации
точки минимума.
Если задача
локализации решена, то в любую точку из
(например, середину) принимают в качестве
приближённого решения задачи (1).
Метод равномерного поиска
Выбираем некоторое
и разбиваем исходный отрезок [
]
на
частей точками
…,
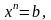где
и поочерёдно начиная с
вычисляем значение функции
.
В силу унимодальности будут выполняться
неравенства
.
Тогда ясно, что
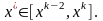
Если
,
то задача локализации решена. В противном
случае выбираем
и разбиваем его на некоторое количество
частей и операцию поиска повторяем. В
конце концов, задача (1) будет решена.
Замечание.
Можно
сразу подобрать
таким образом, чтобы выполнялось
,
но это не рационально, так как количество
точек перебора будет очень большим.
Лучше на 1-ом этапе исходный отрезок
разбить на количество частей
,
потом количество точек увеличить.
6. Минимизация унимодальных функций. Метод Фибоначчи.
Рассм. задачу , (1) где – некоторые числа ( ).
Методы минимизации унимодал. ф-ций. Опр. Ф-ция наз. унимодальной на [ ], если сущ.точка т, что на ф-ция монотонно убывает, а на монотонно возрастает. - оптимал. план задачи (1).
В зад.(1)унимодальная ф-ция имеет единств. оптимал. план и не имеет локал. минимумов. Если в задаче (1) (3) , то ф-ция строго выпукла и явл. унимодальной. Если в зад.(1) ф-ция не унимодальная, то в некоторых случаях [a,b] с помощью нерав-ва (3) её удаётся разбить на интервалы унимодальности, затем чтобы реш. исходную зад.(1) достаточ. на каждом таком отрезке реш. задачу минимизации унимодал. ф-ции и простым перебором найти оптимал. план.
Будем решать задачу (1), в кот. - унимодальная функция. Поставим цель: по заданному найти на [a,b] такую часть (длиною ) и чтобы . Эта задача наз. задачей локализации точки минимума.
Если задача локализации решена, то в любую точку из (например, середину) принимают в качестве приближённого решения задачи (1).
Метод Фибоначчи
Этот метод даёт минимальное количество точек перебора.
Задача: пусть на [ ] позволяется вычислить значение целевой ф-ции не более чем в точках. Требуется так их разместить, чтобы в результате получить интервал локализации наименьшей длины. Эту зад. решает метод Фибоначчи.
Введём числа Фибоначчи:
Существуют
специальные таблицы чисел Фибоначчи,
где
.
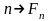В методе Фибоначчи на нулевой итерации
полагают
В дальнейшем используется общая схема двухточечных методов.
Замечание. Иногда задание числа неудобно, тогда возникает другая задача: по данному требуется локализовать в интервале, не превышающую длину , используя минимальное количество вычислений функции .
Эту задачу также решает метод Фибоначчи, но в нём сначала надо найти n- минимальное количество вычислений