7. Минимизация унимодальных функций. Метод золотого сечения.

Рассм. задачу , (1) где – некоторые числа ( ).

Методы минимизации унимодал. ф-ций. Опр. Ф-ция наз. унимодальной на [ ], если сущ.точка т, что на ф-ция монотонно убывает, а на монотонно возрастает. - оптимал. план задачи (1).

В зад.(1)унимодальная ф-ция имеет единств. оптимал. план и не имеет локал. минимумов. Если в задаче (1) (3) , то ф-ция строго выпукла и явл. унимодальной. Если в зад.(1) ф-ция не унимодальная, то в некоторых случаях [a,b] с помощью нерав-ва (3) её удаётся разбить на интервалы унимодальности, затем чтобы реш. исходную зад.(1) достаточ. на каждом таком отрезке реш. задачу минимизации унимодал. ф-ции и простым перебором найти оптимал. план.

Будем решать задачу (1), в кот. - унимодальная функция. Поставим цель: по заданному найти на [a,b] такую часть (длиною ) и чтобы . Эта задача наз. задачей локализации точки минимума.

Если задача локализации решена, то в любую точку из (например, середину) принимают в качестве приближённого решения задачи (1).

Метод золотого сеч. Опр. Точка осуществляет золотое сечение [ ] на две неравные части. Если длина меньшего отрезка так относится к длине большего отр., как длина большего отр. относится к длине [ ], т.е. если выполн.:

Найдём расположение ,для этого подставим 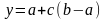и найдём значение :

В методе золотого сечения на нулевой итерации каждая из точек осуществляет золотое сечение [ ] (с разных сторон), в дальнейшем применяется общая схема двух точечных методов.

Метод золотого сечения не намного хуже метода Фибоначчи, справедлива оценка:

Однако в этом методе не требуется указывать ни , ни При большом количестве итераций обычно внутренние точки разбиения обновляются: строятся новые, которые снова осуществляют золотое сечение

8. Градиентные методы. Выбор шага.

Задачу (1) будем решать в 2 этапа:

I этап: построение направлений итерации. Полагаем : где , в результате приходим к задаче: 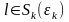(5),где –некоторая окрестность начала координат в размерами . В результате реш-я зад.(5) получаем вектор . Он выбир.за направление на -ой итерации. При выборе направления его размеры не важны, поэтому 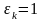, то есть имеет единичную длину. Константа в(5) также на направление не влияет и её отбрасывают. 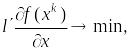Т.обр., для нахождения решается задача: (5*)

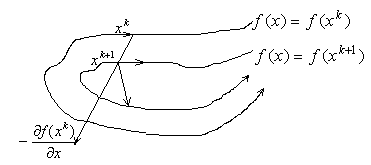
Геометрич. интерпретация «овражной структуры». – линия с постоянной высотой над уровнем океана. В случае «овражной структуры», как правило, градиент имеет большую длину и направлен почти перпендикулярно к направлению ведущему к оптимал. плану.

Замечание. В случае «овражной структуры» надо строить с учётом линий уровня целевой ф-ции, желательно знать кривизну, 2-ую производную. II этап: реш-е зад.(1), когда по известному приближению построено направление выбир. размер окрестности , т.е. определ. размер шага в этом направлении. Наиболее распространены 3 способа:

а) наилучший шаг в заданном направлении, реш. зад. (8)

где . Точное решение задачи (8) выбирается за .

Опр.Метод 1-го порядка, в кот. шаг выбир.в виде (7), а направление наилучшим называется методом наискорейшего спуска. б) , где – малое число, при этом способе на всех итерациях шаг выбирается одинаковым.

Замечание. Если шаг выбрать достаточно большим, то даже если направление позволяет уменьшить целевую функцию, с этим шагом функция возрастёт.

в) метод последовательного дробления. При таком выборе шага задача (8) решается подбором.