13. Динамическое программирование. Задача распределения ресурса. Инвариантное погружение.

Рассматривается подход к решению специальных классов задач, которые имеют характер процессов многошаговых, многоэтапных, развивающихся во времени (динамических).

Общая схема метода динамического программирования

Метод, как правило, включает 3 этапа:

I этап: инвариантное погружение. ; II этап: строится уравнение Беллмана для этой функции. ; III этап: заключается в решении уравнения Беллмана и построению по этому решению оптимального плана исходной задачи.

Задача распределения ресурса. Постановка задачи. Имеется некоторый однотипный ресурс (нефть, зерно) в объёме . Этот ресурс можно использовать в технологических процессах и причём если -му процессу выделить ресурс в объёме , то получим прибыль . Требуется распределить ресурс м-ду процессами так, чтобы суммарная прибыль была максимальной.

Математическая модель. Целевая функция (суммарная прибыль) будет

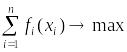(1); Ограничения: (2)

(В (2) можно использовать и нерав-во , но, обычно, ресурс используется полностью.) (3).

(2)-(3) - прямые ограничения. (1)-(3) – математич. модель задачи. Задача (1)-(3) относится к задачам сепарабельного программирования, так как и целевая функция и все ограничения в ней задаются с помощью сепарабельных ф-ций.

Определение. Функция переменных называется сепарабельной, если она представима в виде линейной комбинации функций одной переменной.

К таким задачам всегда применим метод динамического программирования.

Инвариантное погружение для задачи (1)-(3)

Рассмотрим в (1)-(3) первых технологических процесса и выделим для них ресурс в объёме и будем этот ресурс для этих процессов распределять оптимально, тогда приходим к задаче:

(4) это и есть искомое семейство. Если в (4) положить , то придём к исходной задаче (1)-(3). То есть погружение осуществлено корректно. Оптимум целевой функции семейства (4) при фиксированных и , то есть максимальную прибыль, которую можно получить, если распределить среди первых процессов ресурс называется функцией Беллмана и обозначается .

14. Динамическое программирование. Составление уравнения Беллмана.

Рассматривается подход к решению специальных классов задач, которые имеют характер процессов многошаговых, многоэтапных, развивающихся во времени (динамических).

Общая схема метода динамического программирования

Метод, как правило, включает 3 этапа:

I этап: инвариантное погружение. ; II этап: строится уравнение Беллмана для этой функции. ; III этап: заключается в решении уравнения Беллмана и построению по этому решению оптимального плана исходной задачи.

Зафиксируем в (1) параметры и и задачу (1) будем решать следующим образом: последнему -му процессу выделим ресурс в объёме и получим прибыль , тогда процессам останется ресурс в объёме . Предположим, что распределение этого остатка осуществляется оптимальным образом, тогда получим прибыль . В результате такого подхода решение задачи (1) суммарная прибыль: .

Будем изменяться и искать такое значение для него, чтобы получаемая прибыль была наибольшей, то есть будем решать задачу:

(2)

Согласно принципу оптимальности Беллмана оптимальное значение целевой функции задачи (2) равно . То есть выполняется отношение:

(3)

(3) – искомое уравнение Беллмана. Решая задачу (2), мы найдём для неё оптимальный план . Это, очевидно, будет оптимальное количество ресурса, которое выделяется -му ресурсу в задаче (4). То есть оптимальное количество ресурса, которое получает -ый процесс при наилучшем распределении ресурса в объёме ля первых процессов: . Уравнение (3) по динамическому параметру рекуррентно, поэтому для того, чтобы его решить нужно задать для (3) начальные условия. Они получаются, если положить в (1) , тогда приходим к задаче: . Эта задача тривиальна, у неё единственный план и оптимальное значение целевой функции тогда будет:

(4