
- •1. Применимость методов безусловной оптимизации. Задача обслуживания на 1 приборе.
- •2. Общая схема метода ветвей и границ. Задача о рюкзаке.
- •3. Общая схема метода ветвей и границ. Задача целочисленного программирования.
- •4. Метод сплайнов 1 порядка.
- •5. Минимизация унимодальных функций. Равномерный перебор.
- •6. Минимизация унимодальных функций. Метод Фибоначчи.
- •7. Минимизация унимодальных функций. Метод золотого сечения.
- •8. Градиентные методы. Выбор шага.
- •9. Методы 2 порядка. Метод Ньютона.
- •10. Методы условной минимизации. Случай линейных ограничений.
- •11. Методы условной минимизации. Метод штрафных функций.
- •12. Другие методы о выборе метода.
- •13. Динамическое программирование. Задача распределения ресурса. Инвариантное погружение.
- •14. Динамическое программирование. Составление уравнения Беллмана.
- •15. Динамическое программирование. Построение решения.
11. Методы условной минимизации. Метод штрафных функций.
Пусть дана задача: (1)
Методы безусловной минимизации(градиентные,Ньютона и т.д.)можно использ. и для решения зад.(1), но при выборе шага надо учитывать ограничения задачи т., чтобы не вышло за пределы . Обычно на -ой итерации, после того как известно и выбрано вектор подставл. во все ограничения задачи и тогда получаем некоторую совокупность уравнений, неравенств на скалярную переменную . Если эта с-ма имеет ненулевое реш-е, то метод применим и для зад.(1) и для выбора шага на построенной системе ограничений минимизируется ф-ция . Если система ограничений на не имеет решений, то метод не применим.
Общий случай. Метод штрафных функций
Определение.
Пусть дано
некоторое
![]() .
Тогда штрафной
функцией
этого множества называют функцию со
следующими свойствами:
.
Тогда штрафной
функцией
этого множества называют функцию со
следующими свойствами:
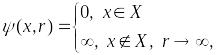
![]() – некоторый неотрицательный скалярный
параметр, с ростом которого неограниченно
растёт функция
– некоторый неотрицательный скалярный
параметр, с ростом которого неограниченно
растёт функция
![]() .
.
Штрафную функцию можно интерпретировать как штраф за отклонение от , а характеризует относительную величину этого штрафа.
Пример 1.
![]() – множество планов задачи с ограничениями
равенствами, то можно положить
– множество планов задачи с ограничениями
равенствами, то можно положить
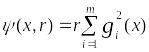 .
.
Существуют специальные способы подбора штрафных ф-ций для разл. типов множеств. Штрафные ф-ции различаются по порядку роста. Существуют штрафные функции, которые имеют полиномиальный рост, экспоненциальный рост, логарифмический рост в зависимости от отклонения от X.
Пусть дана зад.(1) и для построена штрафная ф-ция, тогда метод штрафных ф-ций заключается в решении вместо зад.(1), задачи на безусловный минимум
![]() (7)
(7)
В задаче (7) возможны 2 подхода:
1. составляем для
целевой ф-ции условие стационарности
![]()
Находим стационарную
точку
![]() ,
затем находим точку
,
затем находим точку
![]() (8)
(8)
Иногда, таким образом, удаётся построить в точности оптимальный план.
2. в других случаях задача (7) решается приближёнными методами.
12. Другие методы о выборе метода.
Для зад.(1) популярны
методы многомерного поиска. Самый
простой из них метод покоординатного
спуска:на первой итерации в кач-ве
направления выбир.
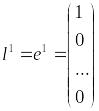 ,
затем подбир.шаг с помощью реш. задачи:
,
затем подбир.шаг с помощью реш. задачи:
![]() (13)
(13)
Замечание. В
этом методе шаг может быть и отрицательный.
Затем полагаем
![]() .
На 2-ой итерации в качестве направления
.
На 2-ой итерации в качестве направления
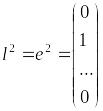 снова реш. зад.(13), находится шаг и строится
снова реш. зад.(13), находится шаг и строится
![]() ,
и так далее. На
,
и так далее. На
![]() -ой
итерации выбир.
-ой
итерации выбир.
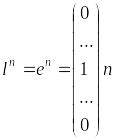 реш. зад.(13) и получаем
реш. зад.(13) и получаем
![]() .
Задача (13) решается методом последовательного
подбора
.
Задача (13) решается методом последовательного
подбора
![]() .
.
Первые
итераций метода дают его полный цикл,
если
![]() нас не удовлетвор., то можно совершить
ещё цикл. В методе покоординатного
спуска на каждой итерации реш.одномерная
зад.минимизации (13)(можно использ.метод
золотого сечения,Фибоначчи)и на каждом
шаге улучшается одна компонента плана.
нас не удовлетвор., то можно совершить
ещё цикл. В методе покоординатного
спуска на каждой итерации реш.одномерная
зад.минимизации (13)(можно использ.метод
золотого сечения,Фибоначчи)и на каждом
шаге улучшается одна компонента плана.
Метод случайного поиска
В этом методе на
-ой
итерации по известному приближению
в качестве
выбир.некоторый случайный вектор
![]() .
При этом использ. механизмы теории
вероятности. После того, как направление
выбрано, провер., явл. ли оно подходящим.
Если выполняется
.
При этом использ. механизмы теории
вероятности. После того, как направление
выбрано, провер., явл. ли оно подходящим.
Если выполняется
![]() ,
для некоторого
,
для некоторого
![]() малого, то
выбир. в качестве направлений итерации
и осуществл. итерация, шаг выбирают по
3-ему способу. Если
малого, то
выбир. в качестве направлений итерации
и осуществл. итерация, шаг выбирают по
3-ему способу. Если
![]() ,
то шаг изменяется на противоположный
либо выбирается по-новому.
,
то шаг изменяется на противоположный
либо выбирается по-новому.
При выборе метода для решения конкретной задачи надо учитывать всю информацию, тип целевой функции, её гладкость, форму поверхности уровня, кривизну и так далее.
