9. Методы 2 порядка. Метод Ньютона.
Рассмотрим задачу:
(1)
В методах 2-го
порядка на
-ой
итерации по известному приближению
реш. Задача
(9),
- квадратичная аппроксимация. Если
окрестность строится с помощью линейных
ограничений, то (9) - задача квадратичного
программирования, её решение –
.
Разл. способы задания окрестности
задают разл. методы. Будем реш.(9) в 2
этапа:
I
этап:
,
.
Тогда придём к задаче:
,
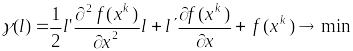(10)
Решение этой задачи принимается за – направление итерации. Шаг выбирается одним из 3-х способов (из 3.3)
Пример. Пусть в задаче (1) выполняется условие
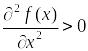(11), то
есть функция является строго выпуклой.
Замечание. Условие
(11) может выполн. в некоторой окрестности
реш-я задачи, тогда и ф-ция
строго выпукла
.
Задача (10) имеет решение, даже если
положить
и будет находиться в стационарной точке
.
Положим в (10)
и составим уравнение стационарности
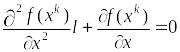
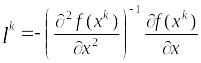(12)
Направление
итерации, которое выбирается по формуле
(12) называется направлением Ньютона, а
методы, основанные на таком либо подобном
направлении, называется ньютоновскими.
В частности. Если положить
,
то получим классический
метод
Ньютона.
Геометрическая
интерпретация направлений Ньютона: в
к линии уровня
строим касательный эллипс:
.
Направление Ньютона ведёт в центр
эллипса. Поэтому методы 2-го порядка
более точные и быстрее сходятся.
10. Методы условной минимизации. Случай линейных ограничений.
Пусть дана задача:
(1)
Методы безусловной
минимизации(градиентные,Ньютона и
т.д.)можно использ. и для решения зад.(1),
но при выборе шага надо учитывать
ограничения задачи т., чтобы
не вышло за пределы
.
Обычно на
-ой
итерации, после того как известно
и
выбрано
вектор
подставл. во все ограничения задачи и
тогда получаем некоторую совокупность
уравнений, неравенств на скалярную
переменную
.
Если эта с-ма имеет ненулевое реш-е, то
метод применим и для зад.(1) и для выбора
шага на построенной системе ограничений
минимизируется ф-ция
.
Если система ограничений на
не имеет решений, то метод не применим.
Случай линейных ограничений
Пусть требуется
решить задачу:
(2)
где
– множество простой структуры, которое
задаётся с помощью ограничений на одну
переменную вида
.
В методах 1-го порядка на -ой итерации по известному решается задача
(3)
Как правило, окрестность в (3) формируется с помощью линейных ограничений. Поэтому задача (3) представляет из себя задачу линейного программирования, её решение принимается за .
Если в задаче (3) вначале искать направление итерации и положить , то в результате придём к задаче
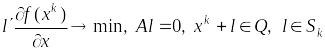(4)
Решение этой задачи принимается за . Задача (4), как правило, линейная задача. После определения направления итерации шаг выбирают одним из описанных 3-х способов.
Пример 1. Положим в (4), тогда получим задачу:
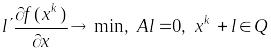(5)
Решение этой задачи называется направлением условного градиента. Это направление даёт наибольшую проекцию на антиградиент и не выводит за пределы .