
- •1. Применимость методов безусловной оптимизации. Задача обслуживания на 1 приборе.
- •2. Общая схема метода ветвей и границ. Задача о рюкзаке.
- •3. Общая схема метода ветвей и границ. Задача целочисленного программирования.
- •4. Метод сплайнов 1 порядка.
- •5. Минимизация унимодальных функций. Равномерный перебор.
- •6. Минимизация унимодальных функций. Метод Фибоначчи.
- •7. Минимизация унимодальных функций. Метод золотого сечения.
- •8. Градиентные методы. Выбор шага.
- •9. Методы 2 порядка. Метод Ньютона.
- •10. Методы условной минимизации. Случай линейных ограничений.
- •11. Методы условной минимизации. Метод штрафных функций.
- •12. Другие методы о выборе метода.
- •13. Динамическое программирование. Задача распределения ресурса. Инвариантное погружение.
- •14. Динамическое программирование. Составление уравнения Беллмана.
- •15. Динамическое программирование. Построение решения.
1. Применимость методов безусловной оптимизации. Задача обслуживания на 1 приборе.
Одну и ту же задачу оптимизации можно реш. разл. методами. Их может быть несколько десятков, поэтому их разбивают на классы. Методы делятся на прямые и непрямые. Непрямой метод–такой,в кот. экстремальная зад. сводится к некоторой др. математич. задаче, например, алгебраической – нахождение стационарных точек. Мы, в основном, будем рассматривать прямые методы.
Пусть дана задача:
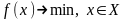 (1)
и пусть
задано начальное приближение
(1)
и пусть
задано начальное приближение
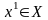 .
В прямых методах строится последовательность:
.
В прямых методах строится последовательность:
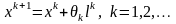 (2)
в кот.
(2)
в кот.
 – направление итерации,
– направление итерации,
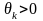 – шаг в этом направлении.Шаг и направление
выбирают,чтобы выполнялось нерав-во:
– шаг в этом направлении.Шаг и направление
выбирают,чтобы выполнялось нерав-во:
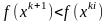 .
Иногда
.
Иногда
 и
и
 можно подобрать, так, чтобы послед-сть
можно подобрать, так, чтобы послед-сть
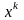 являлась минимизирующей. Обычно в каждом
методе задаётся малая величина
являлась минимизирующей. Обычно в каждом
методе задаётся малая величина
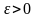 ,
кот. служит для прекращения итерации и
определяет точность метода. Прекращение
итерации обычно осуществл. с помощью
проверки одного из условий:
,
кот. служит для прекращения итерации и
определяет точность метода. Прекращение
итерации обычно осуществл. с помощью
проверки одного из условий:
1

2
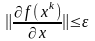
3

Если условие прекращения итерации выполнено, то принимается в качестве приближённого решения задачи.
Методы делятся на детерминированные и стохастические. Если и вычисляются по определённым формулам, то метод называется детерминированным, а если для их построения используются механизмы теории вероятности, то метод называется стохастическим.
Метод называется
методом
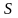 -го
порядка,
если для вычисления направления и шага
итерации используются производные от
параметров задачи до
-ой
включительно. Если
=0,
то такой метод называется методом
поиска или
перебора.
-го
порядка,
если для вычисления направления и шага
итерации используются производные от
параметров задачи до
-ой
включительно. Если
=0,
то такой метод называется методом
поиска или
перебора.
Методы делятся на конечные и бесконечные. Метод называется конечным, если за конечное число итераций удаётся в точности найти оптимальный план.
Методы делятся
на точные и приближённые. В
точных методах
на итерациях преобразуются планы, то
есть
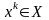
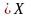 .
В приближённых
методах
могут лежать в
.
В приближённых
методах
могут лежать в
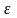 -окрестности
планов.
-окрестности
планов.
Методы также различают по использованию ресурсов ЭВМ, объёму памяти, быстроте нахождения решения и так далее.
2. Общая схема метода ветвей и границ. Задача о рюкзаке.
Метод ветвей и границ явл. одним из самых популярных методов перебора, кот. позволяет сокращать объём перебираемых планов за счёт исключения бесперспективных подмн-в планов, т.е. таких, кот. заведомо не содержат реш-я.
Метод применяют к зад.: ,(1) .
Общая схема. В
методе на каждой итерации строится
список
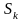 из перспективных подмн-тв, одно из кот.,
по крайне мере содержит оптимал. план.
На нулевой итерации
из перспективных подмн-тв, одно из кот.,
по крайне мере содержит оптимал. план.
На нулевой итерации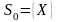 .
Вычисляем оценку итерации
.
Вычисляем оценку итерации
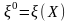 ,
рекорд итерации
,
рекорд итерации
 .
.
Вычисляем разность
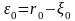 .
Возможны случаи:
.
Возможны случаи:
1.
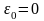 .
В этом случае рекордный план будет
оптимальным планом задачи, так как на
нём достигалась нижняя граница.
.
В этом случае рекордный план будет
оптимальным планом задачи, так как на
нём достигалась нижняя граница.
2.
 ,
где
-малое
положит. число, заданная точность
вычисления. В этом случае рекордный
план можно взять в качестве
-
оптимального, т.е. приближённого реш-я
задачи (1).
,
где
-малое
положит. число, заданная точность
вычисления. В этом случае рекордный
план можно взять в качестве
-
оптимального, т.е. приближённого реш-я
задачи (1).
3.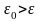 .
Тогда заданная точность не достигнута.
Переходим к первой итерации. Для этого
в соответствие с первым предположением
.
Тогда заданная точность не достигнута.
Переходим к первой итерации. Для этого
в соответствие с первым предположением
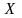 ветвим на более мелкие. Для каждого
вычисл. границу по второму предположению,
и бесперспективные подмн-ва отбрасываем,а
перспективные включаем в список для
1-вой итерации.
ветвим на более мелкие. Для каждого
вычисл. границу по второму предположению,
и бесперспективные подмн-ва отбрасываем,а
перспективные включаем в список для
1-вой итерации.
Постановка зад.
о рюкзаке. Имеется
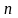 неделимых предметов и для каждого
предмета известно
неделимых предметов и для каждого
предмета известно
 его вес и
его вес и
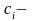 стоимость. Требуется некоторую часть
этих предметов уложить в рюкзак, причём
так, чтобы их суммарная стоимость была
не меньше
стоимость. Требуется некоторую часть
этих предметов уложить в рюкзак, причём
так, чтобы их суммарная стоимость была
не меньше
 ,
и вес рюкзака был минимальным.
,
и вес рюкзака был минимальным.
Математическая
модель. Введём
неизвестные

тогда ограничения
по стоимости будут:
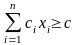 .
Целевая функция:
.
Целевая функция:
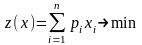 .
Для реш. этой задачи эффективен метод
ветвей и границ.
.
Для реш. этой задачи эффективен метод
ветвей и границ.
