
- •1. Элементы выпуклого анализа.
- •2. Осн. З. Выпуклого программирования. Седловая точка и оптимал. План.
- •3. Теорема Куна-Таккера.
- •4. Критерий оптимальности для гладкой выпуклой задачи.
- •5. Теория двойственности в выпуклом программировании
- •6. Решение одной задачи квадратичного программирования.
- •7. О существовании решения.
- •8. Задача на безусловный минимум.
- •9. Задача с равенствами. Метод исключения.
- •10. Задача с равенствами. Обобщенное правило Лагранжа
- •11. Задача с равенствами. Классическое правило Лагранжа.
- •12. Задача с равенствами. Лемма о включении.
- •13. Задача с равенствами. Необходимое условие 1 порядка.
- •14. Задача с равенствами. Другое доказательство принципа Лагранжа.
- •15. Задача с равенствами. Случай линейных ограничений.
- •16.Задача с равенствами. Условия 2 порядка.
- •17. Задача с неравенствами. Условие 1 порядка.
- •18. Задача с неравенствами. Обобщенное правило Лагранжа.
- •19. Задача с неравенствами. Классическое правило Лагранжа.
- •20. Задача с неравенствами. Условия 2 порядка.
- •21. Векторная оптимизация. Эффективные планы. Усреднение целевых функций.
- •22. Векторная оптимизация. Принципы выбора.
18. Задача с неравенствами. Обобщенное правило Лагранжа.
Пусть дана задача: (1)
Теорема 2. Пусть – локально-оптимальный план задачи (1). Тогда найдётся такой обобщённый вектор Лагранжа , что
1.
2.
![]() ,
не все равные нулю
,
не все равные нулю
3.
![]()
Доказательство.
1. Пусть
– локально-оптимальный план задачи
(1). Тогда справедлива теорема 1, то есть,
несовместна система неравенств (2)-(3).
Применим к ней теорему Фаркаша о
несовместности системы неравенств.
Согласно теореме найдутся такие числа
![]() ,
не все равные нулю, что будет выполняться
условие
,
не все равные нулю, что будет выполняться
условие
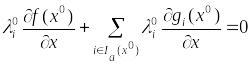 (4)
(4)
Положим тогда остальные =0, и, добавив в (4) нулевые слагаемые, получим:
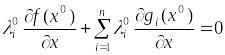 (5)
(5)
Это и есть условие стационарности (1).
2. Условие неотрицательности следует из теоремы Фаркаша.
3. Для получаем:
![]() ,
так как
,
так как
![]() по определению.
по определению.
Для получаем:
,
так как
![]() =0
по предположению.
=0
по предположению.
Ч.т.д.
19. Задача с неравенствами. Классическое правило Лагранжа.
Пусть дана задача: (1)
Определение. Пусть – некоторый план задачи (1). Будем называть его обыкновенным, если вектора
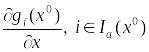 (6)
(6)
линейно независимы.
Теорема 3. Пусть
– обыкновенный локально-оптимальный
план задачи (1). Тогда необходимо найдётся
такой классический вектор Лагранжа
![]() ,
причём единственный (он может быть
нулевым), что выполняется условие:
,
причём единственный (он может быть
нулевым), что выполняется условие:
1.
2.
![]()
3.
![]() .
.
Определение. Задачу (1) будем называть нормальной, если оптимальный план у неё обыкновенный.
Большинство задач вида (1) являются нормальными. Более того, у большинства задач вида (1) все планы обыкновенные. В частности, ясно, что любой внутренний план является обыкновенным.
Определение.
Решение системы
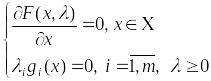 будем называть условно-стационарной
точкой
задачи
(1).
будем называть условно-стационарной
точкой
задачи
(1).
Для нормальных задач принцип Лагранжа можно переформулировать:
Если – локально-оптимальный план, то его нужно искать среди условно-стационарных точек задачи (1).
В случае линейных
ограничений, то есть когда
![]() нетрудно доказать, что всегда справедливо
классическое правило множителей Лагранжа
без предположения обыкновенности
.
нетрудно доказать, что всегда справедливо
классическое правило множителей Лагранжа
без предположения обыкновенности
.
20. Задача с неравенствами. Условия 2 порядка.
Пусть дана задача: (1)
Определение.
Пусть пара
![]() – условно-стационарная точка задачи
(1). Тогда
– условно-стационарная точка задачи
(1). Тогда
![]() ое
ограничение задачи активное на
будем называть жёстким,
если
ое
ограничение задачи активное на
будем называть жёстким,
если
![]() и мягким
или нежёстким,
если
и мягким
или нежёстким,
если
![]() .
.
Обозначим
![]() ,
,
![]() .
.
Ясно, что![]() .
.
Теорема 4
(Необходимое условие оптимальности
второго порядка).
Пусть
−обыкновенный локально-оптимал. план
зад.(1),
![]() − соответствующий ему классический
вектор Лагранжа. То для любого вектора
− соответствующий ему классический
вектор Лагранжа. То для любого вектора
![]() ,
удовлетвор-щего с-ме
,
удовлетвор-щего с-ме
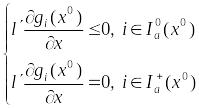 квадратичная
форма
квадратичная
форма
 .
.
Теорема 5 (Достаточное условие оптимальности второго порядка). Пусть – условно-стационарная точка задачи (1), то есть решение системы . Тогда, если для любого вектора , и удовлетворяющего системе квадратичная форма , то – локально-оптимальный план задачи(1).
Теоремы 4 и 5 можно использовать для исключения точек, подозрительных на решение зад.(1), но не являющихся оптимал.
Замеч.
Если рассм. зад.![]() ,
то для неё теоремы 4 и 5 справедливы без
предположения обыкновенности
.
Если рассм. задачу со смешанными
ограничениями
,
то для неё теоремы 4 и 5 справедливы без
предположения обыкновенности
.
Если рассм. задачу со смешанными
ограничениями
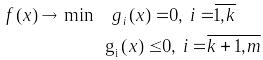 ,
то можно сформулировать принцип Лагранжа
и условия оптимальности второго порядка
простым совмещением результатов
последних двух параграфов.
,
то можно сформулировать принцип Лагранжа
и условия оптимальности второго порядка
простым совмещением результатов
последних двух параграфов.
