7. О существовании решения.
Рассматривается
задача
,
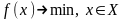(1)
Теорема
(Вейерштрасса).
Если мн-во
– компактно (замкнуто и ограничено) и
на этом множестве функция
,
по крайней мере, непрерывна, то у такой
задачи существует оптимальный план (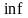
достигается в некоторой точке).
Но не всегда эти условия для задачи выполняются, и у конкретной задачи лин. программир-я может отсутствовать либо в силу неограниченности , либо его незамкнутости, либо из-за разрывности целевой ф-ции и др. причин. Усилим теор. Вейерштрасса.
Определение.
Функция
называется полунепрерывной
в
точке
,
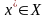если выполняется неравенство:
.
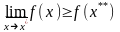Ф-ция полунепрерывна
на
множестве,
если она полунепрерывна снизу в каждой
точке этого множества.
Из непрерывности следует полунепрерывность снизу, обратное – не верно. С другой стороны могут быть функции, которые разрывны в некоторой точке, но полунепрерывны снизу.
В этом случае
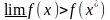и функция в этой точке является
полунепрерывной снизу.
Справедлива обобщенная теорема Вейерштрасса: если в задаче (1) – компакт и функция полунепрерывна на снизу, то у такой задачи существует оптимальный план.
Определение.
.
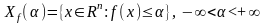Множеством
минимального
уровня
называется
.
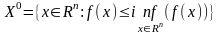Теорема (Критерий
существования).
Для того чтобы у задачи (1) существовал
– оптимальный план необходимо и
достаточно, чтобы для некоторого
конечного числа
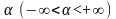множество
было либо непустой частью множества
минимального уровня, либо непустым
компактом, на котором функция
полунепрерывна снизу.
Если задача (1) специфична, то для нее, учитывая ее особенности, иногда можно провести отдельное исследование на существование. В дальнейшем мы будем либо предполагать, что у задачи (1) существует решение, либо, по крайней мере, надеяться на это, либо ставит целью нахождение локального оптимального плана и выбирать из них лучший.
8. Задача на безусловный минимум.
Задача имеет вид:
(1), то
есть
.
Теорема 1. Если
– локально-оптимальный план, то
(2)
Теорема 2
(Необходимое условие оптимальности
второго порядка).
Если
– локально-оптимальный план, то
(3)
Опр. Точка
наз. стационарной
точкой
функции
,
если она является решением системы
(4)
Теор.3
(Достат.
условие оптимальности).
Если
–
стационарная точка ф-ции
и
,
(5)
то
– локально-оптимальный план (1) (по
крайней мере).
Замечание. При проверке условий (3) и (5) применяются критерии Сильвестра неотрицательности и положительности квадратных матриц.
Схема исследования задач типа (1)
1)
Проверяем условие существования решения
задачи (1), при этом применяется критерий
существования решения
.
В общем случае, при
,
вызывает трудности проверка условий
существования решения, так как в редких
случаях можно представить (построить)
множество уровня.
2)
Составляем систему (4) и находим
стационарные точки функции
(все). Только среди них может находиться
оптимальный план и все локально-оптимальные
планы. Пусть
– все стационарные точки функции
.
3) Для каждой стационарной точки проверяем выполнение или невыполнение условий (3)-(5). Пусть – стационарная точка, тогда возможны случаи:
а)
.
Тогда, согласно теореме 3
– локально-оптимальный план.
б)
.
Тогда для нее выполн. условия теор.2, но
не выполн. условия теор.3. Тем не менее,
она остается подозрительной на решение
зад.(1) (т.е. она может оказаться и
оптимальным планом и локально-оптимальным
планом).
в)Не выполн. ни а)ни б).Тогда эту точку исключают из дальнейшего рассмотр-я.
4) Делаем вывод: среди точек, оказавшихся либо локально-оптимал. планами, либо подозрительных на решение, находим лучшую, т.е. подставляем точки в целевую ф-цию и лучшей будет точка с наименьшим значением ф-ции. Если док-но существование реш-я и построены все стационарные точки, то лучшая точка будет оптимал. планом. В общем случае, из-за сложности функции и невозможности найти все решения системы (4) исследование нельзя провести полностью и лучшая точка остается подозрительной на решение задачи.