12. Задача с равенствами. Лемма о включении.

Пусть: (1) и пусть – некоторый произвол. фиксир. план.

Опр. Вектор называется направлением допустимым по ограничениям задачи (1) на плане , если (12)

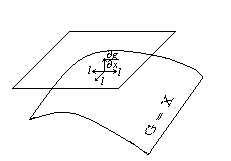На рис. , где – мн-во планов, – касательная плоскость, – вектор нормали. Опр.Вектор будет наз. подходящим направлением для целевой ф-ции зад.(1) на плане , если (13). Если удовлетворяет неравенству (13) и взять вектора , то при достаточно малой : .

Опр.Вектор наз. направлением, подходящим для зад.(1)на плане , если он одновр. явл. и допустимым по ограничениям и подходящим для целевой ф-ции.

Лемма о включении. Пусть – некоторый фиксир. план зад.(1), у кот. , тогда если – обыкновенный план, то для любого вектора и допустимого по ограничениям на , найдутся такие число и ф-ция т., что:

1. – является планами задачи (1));

2. (при малой эти планы лежат в сколь угодно малой окрестности ); 3. .

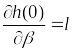Геометрический смысл леммы о включении

Согласно лемме о включении, если на поверхности планов взять обыкновенный план , а в касательной плоскости выбрать некоторое направление, то найдётся такая гладкая линия , которая: 1)лежит на поверхности планов

2) проходит через план при =0 3)Касательный вектор к этой линии обязательно совпадает с выбранным вектором .

Др. словами, любой обыкновенный план можно включить в гладкое семейство планов построенных по некоторому допустимому направлению. Это означает, что каждый обыкновенный план – внутр. точка мн-ва , и он не может быть угловой, изолированной точкой и так далее.

13. Задача с равенствами. Необходимое условие 1 порядка.

Теорема. Пусть – обыкновенный локально-оптимальный план, тогда на нём не найдётся направлений, подходящих к задаче (1), то есть для любого вектора такого, что 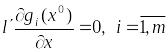(12) следует, что

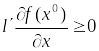(17)

Эта теорема представляет собой необходимое условие оптимальности первого порядка. Это условие носит конструктивный характер. Его можно использовать для улучшения плана задачи (1) следующим образом.

Пусть известен план . Строим задачу линейного программирования:

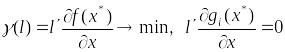(18)

Чтобы существовал оптимальный план в этой задаче необходимо добавить прямые ограничения: .

Решив задачу (18), построим её оптимальный план . Возможны два случая:

1. . Это означает, что является подходящим направлением задачи (1) на . Тогда можно построить планы , где – малая добавка, что будет выполняться неравенство: , то есть при некоторой малой положительной мы построим план лучше, чем . С ним описанную операцию можно повторить и так далее.

2. . Это означает, что на плане не существует направления, подходящего к задаче (1). Согласно доказанной теореме он является подозрительным на решение задачи (1), то есть стационарной точкой.

14. Задача с равенствами. Другое доказательство принципа Лагранжа.

Пусть дана задача: (1)

Пусть − локально оптимальный план этой задачи. Возможны следующие случаи:

1. − обыкновенный локально-оптимальный план, . В этом случае справедливо необходимое условие первого порядка. Применяя тогда к формулам (12), (17) теорему Фаркаша о неравенстве вследствие равенств, приходим к выводу, что найдутся такие числа , что 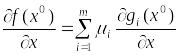. Перенося в этом равенстве все слагаемые влево и полагая , получим условие стационарности: .

А это означает, что в нашем случае справедливо классическое правило множителей Лагранжа. Единственность вектора следует из обыкновенности плана.

2. − обыкновенный локально-оптимальный план, , тогда вектора (7) образуют базис в и любой вектор можно разложить по этому базису. Разложим вектор 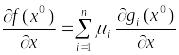. А это равенство снова приводит к условию стационарности, то есть и для второго случая справедливо классическое правило множителей Лагранжа.

3. − не является обыкновенным планом. Тогда вектора (7) зависимы и существует , не все равные нулю, что существует . Положим , и добавим нулевое слагаемое в последней сумме.

.

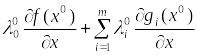Это будет означать, что 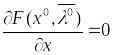и существует . То есть в третьем случае справедливо обобщённое классическое правило множителей Лагранжа.

Принцип Лагранжа доказан, так как других случаев для быть не может.

Замечание. При другом доказательстве использовалось необходимое условие первого порядка и теория двойственности, поэтому принцип Лагранжа выступает как бы двойственным результатом для прямого.